Mogan Gh.L., Butnariu S.L., Buzdugan I.D. Organe de mașini. Lucrări de laborator. Universitatea Transilvania din Brașov

1. PRELUCRAREA ŞI ANALIZA STATISTICĂ A DATELOR EXPERIMENTALE

2.1 ASPECTE GENERALE (Go to 2.1)

2.2 MĂRIMI FIZICE MĂSURABILE (Go to 2.2)

2.2.1 Mărimi fizice variabile măsurate (Go to 2.2.1)

2.2.1.1 Mărimi fizice monovariabile (Go to 2.2.1.1)

2.2.1.2 Mărimi fizice bivariabile (Go to 2.2.1.2)

2.2.1.3 Mărimi fizice multivariabile (Go to 2.2.1.3)

2.2.2 Reprezentări (vizualizări) a datelor (variabilelor) obținute prin măsurare (Go to 2.2.2)

2.2.2.1 Reprezentări tabelare de tip Excel (Go to 2.2.2.1)

2.2.2.2 Reprezentări grafice (Go to 2.2.2.2)

2.3 MĂSURAREA MĂRIMILOR FIZICE. ERORI DE MĂSURARE (Go to 2.3)

2.3.1 Metode de măsurare (Go to 2.3.1)

2.3.2 Erori și precizia de măsurare (Go to 2.3.2)

2.4 ELEMENTE DE TEORIA PRBABILITĂȚILOR APLICATE ÎN STATISTICĂ (Go to 2.4)

2.4.1 Aspecte generale (Go to 2.4.1)

2.4.2 Distribuții (repartiții, legi) probabilistice teoretice (Go to 2.4.2)

2.4.2.1 Distribuția normală (Gauss) (Go to 2.4.2.1)

2.4.2.2 Distribuția normală standard (Go to 2.4.2.2)

2.4.2.3 Distribuția t (Student) (Go to 2.4.2.3)

2.4.2.4 Distribuția F (Fischer) (Go to 2.4.2.4)

2.5 PRELUCRAREA STATISTICĂ A DATELOR EXPERIMENTALE (Go to 2.5)

2.5.1 Aspecte generale (Go to 2.5.1)

2.5.2 Variabile statistice (Go to 2.5.2)

2.5.3 Elemente de statistică descriptivă (Go to 2.5.3)

2.5.3.1 Indicatori statistici descriptvi, generalități (Go to 2.5.3.1)

2.5.3.2 Indicatori statistici ai tendinței centrale (de medie): Media, Mediana, Modul (Go to 2.5.3.2)

2.5.3.3 Indicatori de poziționare (localizare): Maximul/Minimul, Amplitudininea (Range), Caurtile, Percentile (Go to 2.5.3.3)

2.5.3.4 Indicatori statistici ai formei distribuției: Asimetria (Skewness), Boltirea (Kurtosis) (Go to 2.5.3.4)

2.5.3.5 Indicatori statistici de dipsersie (împrăștiere): Dispersia (Variance), Abaterea standard (Standard Deviation), Coieficientul de variație, Eroarea standard (Go to 2.5.3.5)

2.5.3.6 Indicatori statistici de probabilitate: Transformata z, Densitatea de probabilitate (probabilitatea cumulată), Scorul z, Intervalul de încredere (Go to 2.5.3.6)

2.5.3.7 Indicatori statistici de corelare (asociere) a două variabile: Coeficientul de covarianță, Coeficențul de corelație, Matricea de covarianță (Go to 2.5.7.7)

2.5.4 Analize statistice descriptive (Go to 2.5.4)

2.5.4.1 Analize statistice descriptive bazate pe reprezentări grafice ale frecvențelor (Go to 2.5.4.1)

2.5.4.2 Analize statistice descriptive bazate pe reprezentări grafice de tip boxplot (Go to 2.5.4.2)

2.5.4.3 Analize statistice descriptive bazate pe reprezentări grafice a distribuției (repartiției) datelor (Go to 2.5.4.3)

2.5.4.4 Analize statistice descriptive bazate pe valori ale indicatorilor statistici (Go to 2.5.4.4)

2.5.5 Analize statistice inferenţiale (deductive) (Go to 2.5.5)

2.5.5.1 Aspecte generale (Go to 2.5.5.1)

2.5.5.2 Modelarea problemelor de statistică inferențială (Go to 2.5.5.2)

2.5.5.3 Alegerea tipului testului statistic (Go to 2.5.5.3)

2.5.5.4 Descrierea (formularea) problemei statistice (Go to 2.5.5.4)

2.5.5.5 Algoritm general de rezolvare a testelor statistice de decizie (Go to 2.5.5.5)

2.5.5.6 Analize (teste) statistice de decizie/estimare (Go to 2.5.5.6)

2.5.5.6.1 Aplicație testul z de medie pentru o variabilă (Go to 2.5.5.6.1)

2.5.5.6.2 Aplicație testul t de medie pentru o variabilă (Go to 2.5.5.6.2)

2.5.5.6.3 Aplicație t-test de medie pentru două variabile pereche (dependente) (Go to 2.5.5.6.3)

2.5.5.6.4 Aplicație t-test de medie pentru două variabile nepereche (independente) cu dispersii egale (Go to 2.5.5.6.4)

2.5.5.6.5 Aplicație t-test de medie pentru două variabile nepereche (independente) cu dispersii inegale (Go to 2.5.5.6.5)

2.5.5.6.6 Aplicație testul F de dispersie pentru două variabile (Go to 2.5.5.6.6)

2.5.5.6.7 Aplicație ANOVA cu un singur factor (one-way ANOVA, Single Factor)

(Go to 2.5.5.6.7)

2.5.5.6.8 Aplicație testul ANOVA cu doi factori fără replicație (ANOVA: Two-Factor Without Replication) (Go to 2.5.5.6.8)

2.5.5.6.9 Aplicație testul ANOVA cu doi factori cu replicație (ANOVA: Two-Factor with Replication) (Go to 2.5.5.6.9)

2.5.5.7 Analize inferențiale de corelare și regresie (Go to 2.5.7)

2.5.5.7.1 Aplicație de analiza corelației a două variabile (Go to 2.5.7.1)

2.5.5.7.2 Aplicație de analiza regresiei liniare simplă (Go to 2.5.7.2)

2.6 BAZELE STUDIILOR EXPERIMENTALE PRIN MĂSURĂTORI (Go to 2.6)

2.6.1 Aspecte generale (Go to 2.6.1)

2.6.2 Planificarea (proiectarea) experimentelor unifactoriale (Go to 2.6.2)

2.6.2.1 Definirea și enunțul problemei (Go to 2.6.2.1)

2.6.2.2 Scopul și obiectivele cercetării experimentale (Go to 2.6.2.2)

2.6.2.3 Stabilirea populației țintă (de interes) și a ipotezelor statistice (Go to 2.6.2.3)

2.6.2.4 Determinarea volumului (mărimii) eșantionului (Go to 2.6.2.4)

2.6.3 Realizarea experimentelor, colectarea şi/sau achiziţia datelor (Go to 2.6.3)

2.6.3.1 Colectarea datelor prin chestionare (online) (Go to 2.6.3.1)

2.6.3.2 Achiziţia automată a datelor (Go to 2.6.3.2)

2.6.4 Prelucrarea statistică şi analiza datelor (Go to 2.6.4)

2.6.4.1 Analiza primară a datelor (Go to 2.6.4.1)

2.6.4.2 Prelucrarea statistică și analiza finală (Go to 2.6.4.2)

2.6.5 Interpretarea rezultatelor şi elaborarea concluziilor (Go to 2.6.5)

2.1 ASPECTE GENERALE

Cercetarea ştiinţifică experimentală ca investigaţie practică urmăreşte, pe de-o parte, descoperirea şi descrierea de noi cunoştinţe (fenomene, procese, legi etc.) şi, pe de altă parte, verificarea unor cunoştinţe obţinute pe alte căi (teoretice, teoretico-experimentale, empirice etc.). Cercetările experimentale de verificare a unor legităţi ca parte importantă a cercetării ştiinţifice au la bază măsurători repetate ale unuia sau mai multor parametri prin care se pot studia variaţiiile şi influenţele unuia sau mai multor factori asupra unui proces definit teoretic anterior. Pentru o bună validare dar şi pentru o bună eficenţă economică numărul măsurătorilor, numit eşantion, este limitat la valori, de obicei, determinate de tipul paramatrului măsurat, instalaţia experimentală, metodoligia de prelucrare a rezultatelor etc.

Scopul cercetărilor experimentale de verificare, bazate pe rezultate obţinute pentru unul sau mai multe eşantione (numere limitate de măsurători), este de generalizare, prin prelucrări statistice, a rezultatelor obţinute pentru acesta la toate valorile posibile (de obicei, infinite), validând astfel modelul studiat. În funcţie de numărul de factori de influenţă se pot utiliza diverse metode probabilistic-statistice pentru prelucrarea datelor experimentale, care permit analize şi interpretări statistice precise şi deci sintetizarea unor concluzii de validare riguroase.

2.2 MĂRIMI FIZICE MĂSURABILE

În inginerie mărimile asociate unor parametri fizici (ex. masa, presiunea, forţa etc.) pot fi evaluate şi exprimate numeric, în urma măsurătorilor (experimentelor), de obicei, prin variabile cu diferite valori, care nu se cunosc dinainte. Mărimile măsurabile, ca manifestări ale proprietăţilor unui obiect sau proces fizic, în funcţie de modul de reprezentare pot fi scalare: scalare, caracterizate de un singur număr; vectoriale, caracterizate de modul, direcţie şi sens; tensoriale exprimate prin matrice și în funcţie de varaţia în timp: constante şi variabile (determinist sau aleatorii)

2.2.1 Mărimi fizice variabile măsurate

În cadrul cercetărilor experimentale se constată că valorile numerice măsurate pot fi diferite chiar dacă rămân nemodificate condiţiile de desfăşurare ale măsurătorilor. Astfel, descrierea unui set de date obținute prin măsurători se face cu variabila aleatoare ale cărei valori caracterizează mărimea măsurată privită din două puncte de vedere: cantitativ, prin valoarea numerică și calitativ, prin frecvenţa de apariţie a valorii numerice în setul de date. Dacă valorile numerice ale unui set de date aparţin mulţimii numerelor întregi atunci se defineşte o variabilă aleatoare discretă, iar în cazul în care valorile sunt reale se defineşte o variabilă aleatoare continuă.

2.2.1.1 Mărimi fizice monovariabile

În urma măsurării, în condiții practic identice, a unei mărimi fizice, de obicei, independentă (neinfluență de alte mărimi fizice), se poate obține un set de valori {x₁, x₂ … x_n, … x_i}, deseori repetitive, care formează o monovariabilă, x = {x₁, x₂ … x_n} cu n valori.

2.2.1.2 Mărimi fizice bivariabile

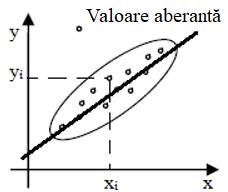
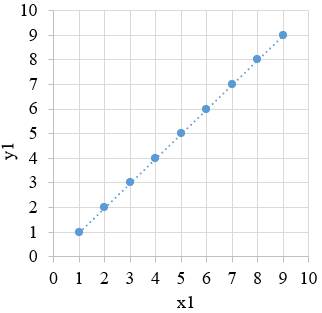
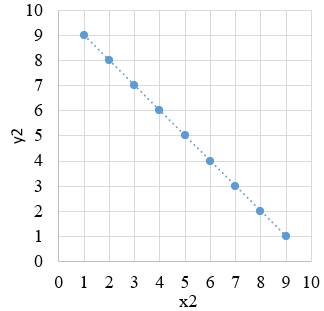
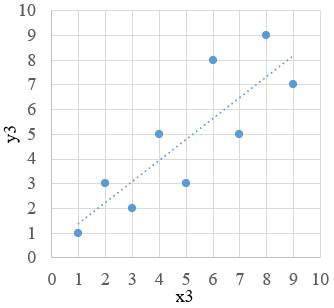
În cazul obținerii prin măsurare a două variabile x = {x₁, x₂ … x_n} și y = {y₁, y₂ … y_n} se pune problema corelării datelor obţinute în vederea stabilirii unei dependenţe matematice între valorile măsurate bazată pe o funcţie, y = f(x).

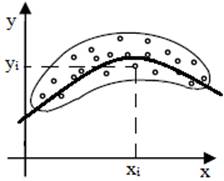
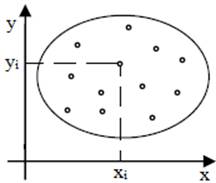
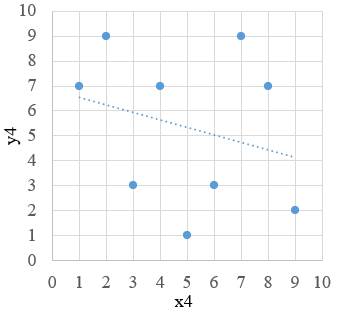
Diagrama de împrăştiere a perechilor (x_i, y_i) într-un sistem de coordonatele x şi y (fig. 2.1) indică, în funcţie de forma norului de puncte, tipul relaţiei (funcţiei) matematice dintre variabile care poate fi, liniară (funcţie polinomială de gradul I, fig. 2.1,a) sau neliniară curbilinie (fig. 2.1,b): (funcţie polinomială de gradul II (parabolă), exponenţială, logaritmică, hiperbolă etc.). Dacă în urma analizei vizuale și/sau statistice nu se distinge nicio tendinţă se apreciază că variabilele nu sunt corelate (fig. 2.1,c). Gruparea datelor experimentale reprezentate pe diagrama de împrăștiere (dispersie) indică, pe lângă posibilitatea aprecierii tipului (formei) funcţiei, şi valorile eronate (aberante, fig. 2.1,a), ce diferă mult de celelalte puncte; pentru diminuarea erorilor aceste valori este bine să fie excluse din prelucrarea ulterioară a datelor experimentale.

a b c

Fig. 2.1 Diagrame de împrăștiere a valorilor seturilor de date: a – liniară; b – curbilinie; c – necorelate

Din punct de vedere al abordării cercetării experimentale pot fi trei cazuri. Primul caz, presupune verificarea unei funcţii cunoscută teoretic, asociată unei legi fizice. În al doilea caz, nu se cunoaște, nici chiar, forma (tipul) dependentei f(x) şi prin metode statistice se realizează corelarea datelor prin estimarea unor dependente tipice din punct de vedere matematic (polinom, putere, exponențială, logaritmică etc.) uramată de testarea statistică a acestora. Astfel, se obțin relaţii empirice, bazate în totalitate pe analiza statistică a datelor experimentale. 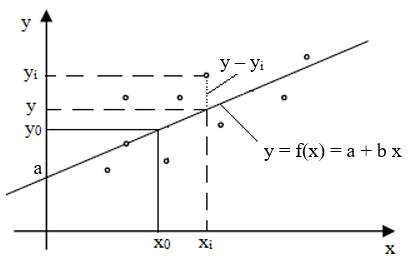În cel de-al treilea caz, pornind de la o funcție asociată unei legi fizice cu parametri necunoscuți ale căror valori se determină prin teste statistice, se obțin funcții semi-empirice.

Deoarece, valorile obţinute prin măsurare, din cauza erorilor de măsurare întâmplătoare, nu se află pe o linie predefinită (punctele sunt împrăștiate), pentru perechile de valori (x_i, y_i), i=1…n, se urmăreşte studierea asocierii şi relaţiei dintre acestea. Asocierea valorilor celor două variabile presupune estimarea intensităţii legăturii dintre acestea (mărimile măsurate) pentru găsirea unei relaţii (funcții) matematice care să exprime variabila dependentă (y) în funcție de variabila independentă (x). Cuantificarea intensităţii unei legături dintre cele două variabile, de obicei, prin determinarea coeficientului de corelație (v.subcap.2.5.3.7). Cea mai utilizată tehnică de determinare a unei relații (funcții) dintre valorile măsurate este regresia care presupune determinarea parametrilor unei linii (drepte sau curbe) care unește “cel mai bine” datele reprezentate prin puncte; pentru aceasta sunt folosite, în special, în studii statistice de estimare și predicţie (v.subcap.2.5.5.7.2).

Regresia liniară simplă (cu două variabile, x și y) are la bază o relație polinomială de gradul întâi (fig. 2.2) între cele două variabile, una independentă (x) și alta dependentă (y). Dreapta de regresie ca cea mai simplă dependenţă matematică a valorii prezisă (estimată) a variabilei dependente y de variabilă independentă x poate fi definită sub forma canonică, y = f(x) = a + b x, în care, a este termenul liber (ordonata la origine, valoarea pentru x = 0) și b coeficientul de regresie (panta dreptei, coeficientul unghiular). Valorile pozitive ale pantei b indică faptul că dreapta se înclină în sus cu creşterea variabilei independente x (legătura între variabile este pozitivă, directă), iar valorile negative ale acesteia indică faptul că linia se înclină spre în jos (legătura între variabile este negativă, inversă). Dacă, b = 0, nu există legătură între variabile.

Fig. 2.2 Regresia lniară simplă

Pentru a determina linia de regresie „cea mai bună” se utilizează, frecvent, metoda celor mai mici pătrate (Legendre, 1806) care presupune minimizarea sumei pătratelor distanţelor, y – y_i (erori sau reziduuri),

S = = → minim.

Pentru ca S să fie minimă, derivatele de ordinul întâi ale acesteia, în raport cu necunoscutele a şi b, egalate cu zero, formează un sistem algebric liniar cu soluţia unică,

a = ,

b = .

Deși regresia liniară se poate realiza și manual, calculele sunt efectuate mult mai ușor dacă se utilizează pachete software specializate, dintre care, frecvent, este utilizat Microsoft Excel (v.Ghid.Ap.2.21 ).

Indiferent de gradul de împrăştiere al punctelor totdeauna se poate găsi o dreaptă de regresie care uneori nu estimează cu precizie variabilele măsurate şi deci, după obţinerea celor doi parametri, a şi b, este necesar ca funcţia de regresie liniara să fie verificată prin teste statistice de semnificaţie la nivel global și, inclusiv, la nivel de parametrii acesteia (v.subcap.2.5.5.7.2). Astfel considerând  funcţia de regresie a priori valabilă, se vor aprecia statistic valorile parametrilor (a şi b) care se abat mai mult sau mai puțin de la valorile prezise, cu o probabilitae impusă.

Dreapta de regresie se poate utiliza ca bază pentru predicţia (estimarea) valorilor variabilei dependente. Astfel, pentru valoarea x₀, valoarea prognozată (estimată) pentru y este y0, ordonata de pe dreapta de regresie (fig. 2.2).

2.2.1.3 Mărimi fizice multivariabile

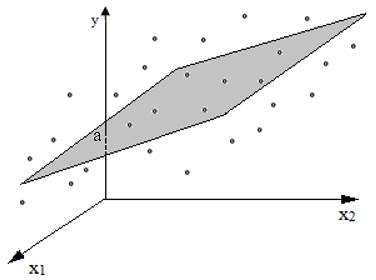
Scopul regresiei multiple este de a determina o relaţia de depentență dintre o variabilă dependentă și două sau mai multe seturi de variabile independente. În cazul cel mai simplu, cu două variabile independente, relația de dependență este o extensie a regresiei simple, numită regresie biliniară. În fig. 2.3 se prezintă diagrama de împrăştiere asociată funcţiei de regresie cu o variabilă dependentă y şi două seturi de variabile independente x₁ şi x₂.

Funcţia de regresie multiplă are la bază relația,

y = a + b₁ x₁ + … b_i x_i + … b_p x_p,

în care, x₁, x₂, … x_p sunt seturile de variabile independente; a – termenul liber, dependent de factorii neincluşi în model considerat constant; b_i (i = 1…p), coeficienţi parţiali de regresie asociaţi seturilor variabilelor dependente care arată cu câte unităţi se modifică variabila dependentă la modificarea cu o unitate a variabilei i iar celelalte variabile sunt menţinute constante.

Fig. 2.3 Regresia biliniară

2.2.2 Reprezentări (vizualizări) a datelor (variabilelor) obținute prin măsurare

În vederea organizării și sistematizării datelor pentru prelucrarea statistică, pentru a fi mai ușor de interpretat ulterior, se generează tabele și grafice care pot sta la baza studiilor ulterioare. Dintre pachetele software de prelucrare a datelor, cu precădere, tabelar se remarcă, prin generalitate, simplitate și eficacitate pachetul Microsoft Excel care poate fi folosit și pentru prelucrarea statistică a datelor experimentale (v.Ghid.Excel.01).

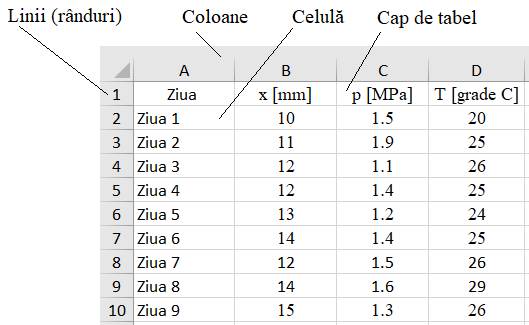
2.2.2.1 Reprezentări tabelare de tip Excel

Un tabel Excel este compus din mai multe celule organizate pe linii și coloane (fig. 2.4). Fiecare celulă se poate localiza prin intermediul unei etichete compusă din codul coloanei (o literă a alfabetului de la A la Z) și al liniei (numărul, 1,2,3…), de ex. celula A7, B3, D9 etc. Conținutul unei celule se poate edita și/sau modifica direct prin introducerea unei date, sau prin execuția unei funcții predefinită.

Fig. 2.4 Tabel Excel

În general, un tablel trebuie să conțină denumirile liniilor și capul de tabel cu precizarea denumirii mărimilor fizice și a unităților de măsură ale acestora. În vederea prelucrărilor statistice, seturile de date obținute prin măsurători, de obicei, conțin valori aleatorii care pot fi repetabile, sunt organizate tabular ca diverse șiruri de valori: crescătoare sau descrescătoare, pe grupe (intervale, clase) etc.

2.2.2.2 Reprezentări grafice

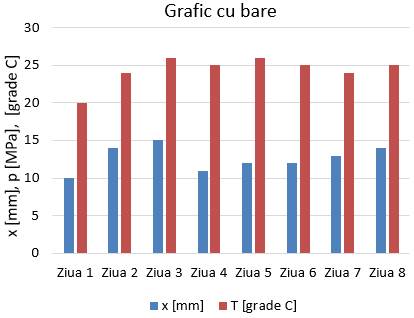
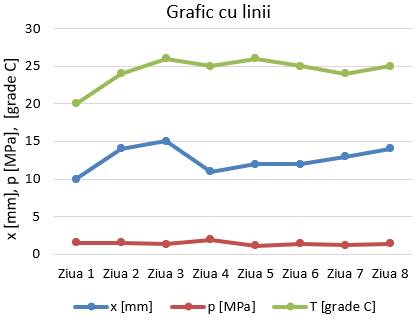
În vederea interpretării datelor obținute prin măsurători repetate (aleatorii), deosebit de utile sunt reprezentările grafice: cu puncte (scatter), cu bare, linii, histograme, boxploturi etc. Un grafic, pentru lizibilitate sporită, trebuie să conțină: titlu, legendă, denumirea axelor, unitățile de măsură asociate mărimilor fizice etc.

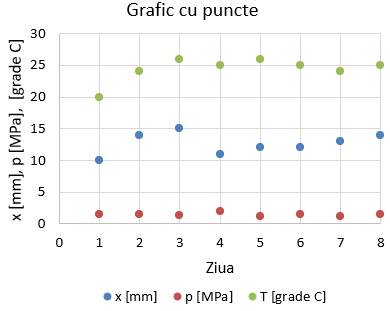
Grafice cu bare (fig. 2.5,a) prezintă datele cu ajutorul unor linii (bare), orizontale sau verticale, cu lungimi diferite.

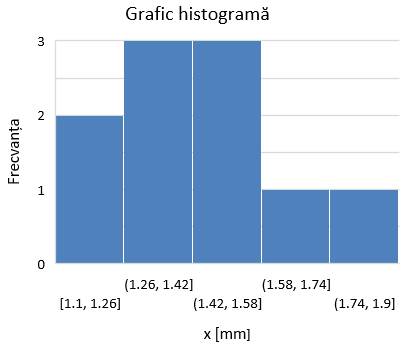
Grafice cu puncte și/sau cu linii (fig. 2.5,b,c) prezintă datele cu ajutorul unor puncte și/sau cu linii care le conectează.

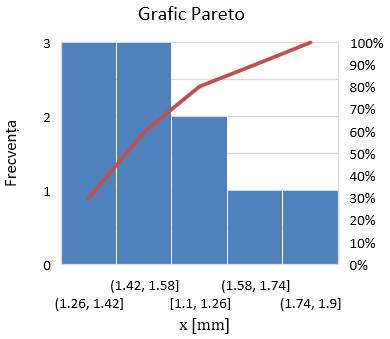
Grafice de tip histograma (fig. 2.5,d) utilizează blocuri verticale cu diverse lungimi cărora li se asociază mărimi omogene (de ex.frecvențele) cu valoril cuprinse în diverse grupuri (intervale, clase); aceste grafice sunt folosite frecvent pentru prelucrări statistice.

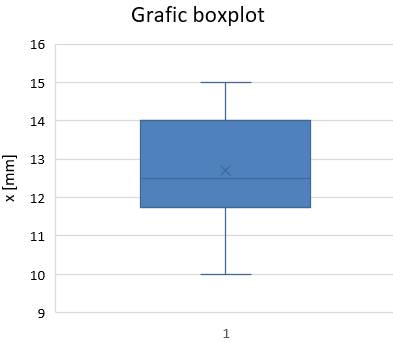
Graficele Pareto (histogramă sortată, fig. 2.5,e) conțin coloane sortate în ordine descendentă a unor mărimi omogene (de ex. frecvențe) cu valori cuprinse în diverse grupuri (intervale, clase) și o linie care reprezintă variația mărimii cumulată (de obicei, în %); aceste grafice evidențiază cele mai frecvente valori dintr-un set de date și sunt folosite, cu precădere, pentru analize de calitatea produselor/proceselor.

Graficele boxplot (fig. 2.5,d) reprezintă datele prin intermediul unui simbol grafic care se descrie prin intermediul unor parametri cu semnificații statistice (v.subcap.2.5.4.2)

a	b
c	d
e	f
Fig. 2.5 Grafice asociate datelor: a – cu bare; b – cu puncte; c – cu linii; d – histogramă; e – Pareto; f – boxplot

2.3 MĂSURAREA MĂRIMILOR FIZICE. ERORI DE MĂSURARE

2.3.1 Metode de măsurare

Măsurarea, în inginerie, este procesul de determinare experimental a valorilor unor mărimi fizice (parametri) asociată unui fenomen, obiect sau proces (sistem) fizic. Aceasta bazat pe pincipii, metode și mijloace specifice are scopul determinării unor valori ale mărimii măsurate apropiate cât mai mult de valoarea reală a acesteia.

Metodele de măsurare, după modul de obținere a valoilor mărimii fizice, pot fi directe, când valoarea măsurată se compară cu unitatea de măsură (etalon) sau indirecte, prin care se obține o mărime necunoscută (y) având la bază mai multe valori măsurate direct (x₁, x₂, x₃ …) considerate interdependente printr-o relație dată (y = f(x₁, x₂, x₃ …)); în acest fel se determină o valoare ca efect al unor mărimi măsurate (de ex. determinarea temperaturii ca efect al modificării rezistenței electrice). Pe de altă parte, după tipul datelor achiziționate, metodele de măsurare pot fi pasive, când datele achiziționate sunt mărimi statice (constante în timp) sau de echilibru (de ex. temperatura unui corp), sau active, ce determină mărimi dinamice (variable în timp) ca răspunsuri ale unui sistem (de ex. amplitudinile și frecvențele vibrațiilor unui sistem mecanic ca urmare a excitației cu oscilații periodice); metodele active, deoarece, permit verificarea, modelarea și validarea sistemelor dinamice, sunt numite și de identificare.

2.3.2 Erori și precizia de măsurare

Valorile de măsurare, indiferent cât de riguros ar fi obținute, sunt afectate de erori sau incertitudini, ale căror cauze pot fi legate de: metoda de măsurare, sensibilitatea instrumentelor de măsură, caracteristicile mediului ambiant, performanțele biologice ale operatorului, elementul/sistemul supus măsurării etc. Abilitatea cercetătorului de a evalua erorile şi/sau incertitudinile cu scopul de a le minimiza este esenţială în cercetarea ştiinţifică.

Se cunoaşte faptul că dacă o mărime se măsoară de mai multe ori, de fiecare dată se obţine o altă valoare chiar dacă măsurătorile se desfăşoară în aceleaşi condiţii, de către acelaşi operator şi cu aceleași instrumente. Cauza acestor neconcordanţe este indusă de erorile de măsurare care fac ca valoarea adevărată (reală) a mărimii măsurate să nu poată fi determinată. Astfel, în practică, se caută să se determine o valoare cât mai apropiată de aceasta cu un prag (nivel) mai mare sau mai mic de apropiere (de obicei, evaluat statistic) în funcţie de scopul experimentelor. Apropierea mărimii determinată prin măsurare de valoarea adevărată (reală, necunoscută) se apreciază global prin precizia măsurătorii. 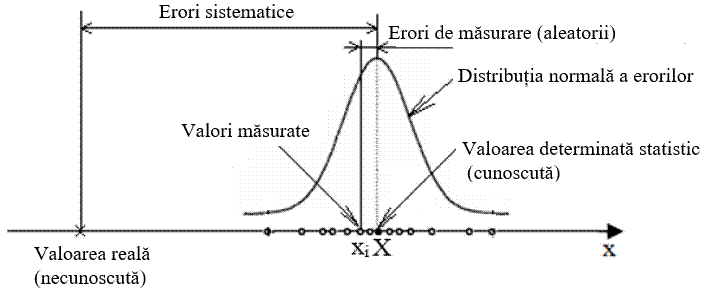Există două mari grupe de erori de măsurare: sistematice și accidentale (întâmplătoare).

Erorile sistematice apar din cauza reglărilor sau etalonărilor incorecte ale aparatelor de măsură, abaterilor asociate operatorului (de ex. de paralaxă) şi/sau a caracteristicilor mediului în care se fac măsurătorile (temperatura, umiditatea, altitudinea etc.). Aceste erori rămân constante atât ca valoare cât şi ca semn pentru măsurări repetate în condiţii identice. Diminuarea efectelor acestor erori asupra rezultatului se face prin calibrări și/sau corecţii care presupun însumarea unei constante sau înmulţirea cu un factor constant a rezultatelor măsurării. Pentru prelucrarea statistică nu se iau în considerare erorile sistematice, de obicei, acestea fiind corectate, preliminar. Astfel, se impune la începerea experimentelor o verificare atentă a stării aparatelor, a condiţiilor de lucru și, dacă este cazul, chiar a unor de calibrări.

Erorile întâmplătoare (aleatorii, accidentale, statistice) apar la măsurări repetate în condiţii cvasiidentice (efectuate de acelaşi experimentator, în aceleaşi condiţii şi cu aceleaşi aparate) ale aceleiași mărimi care variază imprevizibil, atât ca valoare cât şi, uneori, ca semn. Precizia datelor şi deci și a rezultatelor este influențată de erori care provin ca urmare a unor modificări temporale, spațiale, legate de operator, de mediu etc. de la o măsurătoare la alta. Astfel, după n măsuri ale unei mărimi constante x, în condiții practic identice, se obțin n valori rezultate (x₁, x₂ … x_n). Aceste valori, includ erori, și sunt procesate statistic fiind încadrate, de obicei, în legi de distribuție teoretice (de referință). Ca urmare, prelucrarea statistică a valorilor măsurătorilor efectuate asupra unei mărimi, urmăreşte obţinerea “celei mai bune valori” care asigură eroarea minimă între valoarea determinată şi valoarea adevărată.

În fig. 2.6,a se prezintă legea distribuției normale a erorilor aleatorii, frecvent utilizată în practică. Cauzele erorilor aleatorii (imperfecţiunea organelor de simţ, deformări sau deplasări imperceptibile ale componentelor instrumentelor de măsură, variaţii ale stărilor mediului exterior etc.) sunt greu de sesizat putând fi diminuate, dar nu eliminate. Spre deosebire de erorile sistematice, care pot fi compensate prin aplicarea unei corecții (prin sumare sau multiplicare), efectele erorilor aleatorii pot fi diminuate prin creșterea numărului de măsurători. Atunci când se efectuează un număr mic de determinări experimentale a unei mărimi fizice este posibil să apară erori întâmplătoare grosoiere. Dacă într-un set de date redus (cu puţine valori măsurate), există una sau mai multe valori care diferă mult faţă de celelalte, acestea se elimină şi/sau se repetă măsurătorile. În concluzie, dacă erorile sistematice, în cazul când sunt cunoscute, pot fi corectate, cele accidentale nu pot fi evitate şi pentru diminuarea efectelor negative se măreşte numărul de măsurători. Valoarea adevărată (reală) poate fi doar aproximată, precizia aproximării fiind influenţată de erori care se impune să fie evaluate; dintre acestea unele pot fi eliminate şi altele pe cât posibil diminuate.

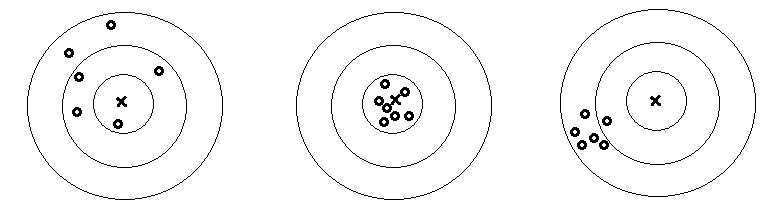
a

b c d

Fig. 2.6 Distribuția erorilor: a – unidirecțional după curba normală (clopotul lui Gauss); b – bidirecțională, imprecisă; c – bidirecțională, precisă și exactă; d – bidirecțională, inexactă

Precizia de măsurare este dată de mărimea intervalului în care sunt incluse erorile. Valorile erorilor de măsurare sunt grupate în jurul unei valori medii, care sintetizează valorile măsurate. Cu cât dimensiunea acestui interval este mai mică, cu atât precizia măsurării este mai mare. Pentru asigurarea (verificarea) corectitudinii (preciziei) unui studiu ştiinţific experimental, prin evitarea obţinerii de rezultate false (sau cu abateri grosolane), se impune evaluarea (prezicerea) erorilor de măsurare. În cazul în care se impune măsurarea unei mărimi fizice, considerată cvasireală, a cărei valoare este cunoscută din literatura de specialitate, se foloseşte și noţiunea de acurateţe (exactitatea) de măsurare care indică abaterea (apropierea) centrului câmpului distribuţiei erorilor valorilor măsurate de valoarea cunoscută. Cu cât această abatere este mai redusă cu atât acurateţea rezultatelor este mai mare (acestea fiind precise și exacte) și dacă abaterea este mărită rezultatele sunt inexacte. Astfel, în practică, se pot întâlni următoarele cazuri de măsurători: imprecise, cu câmpul de distribuție a erorilor larg (fig. 2.6,b); precise și exacte cu câmpul de distribuție a erorilor îngust și cu centrul acestuia apropiat de valoarea reală (fig. 2.6,b); inexacte cu abaterea centrului câmpului de distribuție a erorilor mare (fig. 2.6,b).

Pentru valorile variabilei, x = {x₁, x₂ … x_n}, obținute prin măsurare, se pot determina următoarele erori: absolută ca diferenţa dintre rezultatul unei măsurării x_i şi valoarea cuoscută a acesteia, deseori diferită de ce reală (adevărată), a mărimii măsurate, E = x_i – X și relativă ca raport dintre eroarea absolută şi valoarea cunoscută, E_r = 100 E/X [%]. Deoarece, abaterea (eroarea) globală asociată unui set de date nu poate fi determinată de abaterile individuale este necesar să se apeleze la metode (tehnici) statistice care au la bază metode probabilistice. În practica măsurătorilor se impune realizarea mai multor seturi de măsurători care apoi pot fi prelucrate și comparate cu metode (tehnici) statistice care urmăresc evidenţierea gradului de acceptare a abaterilor bazat pe un criteriu probabilistic. Dacă două seturi de rezultate experimentale reproductibile se cavsisuprapun, în limita erorilor acceptabile, se consideră că cele două rezultate sunt în concordanţă. Dacă diferenţa dintre cele două rezultate experimentale este mare, faţă de valori ale erorilor impuse se consideră că există un dezacord (discrepanţă) între cele două seturi rezultate. De cele mai multe ori parametrii statistici ai cazului general (populația cu numărul de valori, n → ∞), considerat teoretic, sunt estimaţi sau chiar validați de parametrii statistici ai eşantionului (număr de valori, n, redus).

2.4 ELEMENTE DE TEORIA PRBABILITĂȚILOR APLICATE ÎN STATISTICĂ

2.4.1 Aspecte generale

Unui set de date asociate unor măsurători, {x₂, x₁, x₉, x₂, x₁, … x_n …} cu n valori sintetizate în variabila aleatoare x = {x₁, x₂ … x_i … x_n}, i se poate asocia mulţimea frecvențelor, f = {f₁, f₂ … f_i … f_n}, respectiv, a probabilităţilor, p = {p₁, p₂ … p_i, … p_n} cu valori determinte bazat pe frecvențe, p_i = f_i/ (probabilitatea egală cu frecvența relativă); această mulțime, numită distribuţia de probabilitate, are proprietatea = 1.

Valoarea mediei (media aritmetică) a variabilei x, m = /, este un indicator caracteristic care reprezintă o valoare centrală în jurul căreia se găsesc majoritatea valorilor x_i (fig. 2.8,a). Deoarece, suma abaterilor individuale ale variabilei x, ε_i = x_i - m (pozitive şi negative), față de media aritmetică este nulă, = 0, aceasta nu poate fi folosită ca indicator global de apreciere a împrăștierii valorilor erorilor.

Ex.2.1 Setului de date observate, {18, 15, 17, 15, 18, 13, 19, 15, 10, 16, 17, 11, 16, 13, 14, 15, 17, 13, 16, 17, 16, 12, 16, 14}, care reprezintă temperaturile indicate de un termometru într-o perioadă de timp, cu variabila aleatorie (temperaturile observate), x = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19}, i se asociază mulțimea frecvențelor de apariție a valorilor variabilei, f = {1, 1, 2, 2, 3, 4, 5, 4, 2, 1}, respectiv, mulțimea probabilităților, p = {1/25, 1/25, 2/25, 2/25, 3/25, 4/25, 5/25, 4/25, 2/25, 1/25}= {0,04, 0,04, 0,08, 0,08, 0,08, 0,16, 0,2, 0,16, 0,08, 0,04} ; = 1; media aritmetică a valorilor variabilei x, m = /10 = 14,5 ^oC; abaterile (erorile) ε_i = x_i-m ={10-14,5, 11-14,5, 12-14,5, 13-14,5, 14-14,5, 15-14,5, 16-14,5, 17-14,5, 18-14,5, 19-14,5}={-4,5, -3,5, -2,5, -1,5, -0,5, 0,5, 1,5, 2,5, 3,5, 4,5}suma abaterilor de poziționare a valorilor variabilei x față de media aritmetică este nulă, = – 14,5) = 0. În fig. 2.7 se prezintă graficele frecvențelor variabilelor, probabilităților variabilelor, și frecvențelor erorilor la nivel general (fig. 2.7,a,b,c ) și, respectiv personalizate (fig. 2.7,d,e,f) pentru valorile considerate în Ex.2.1.

a b c

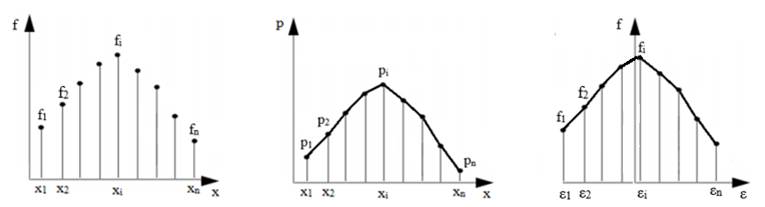
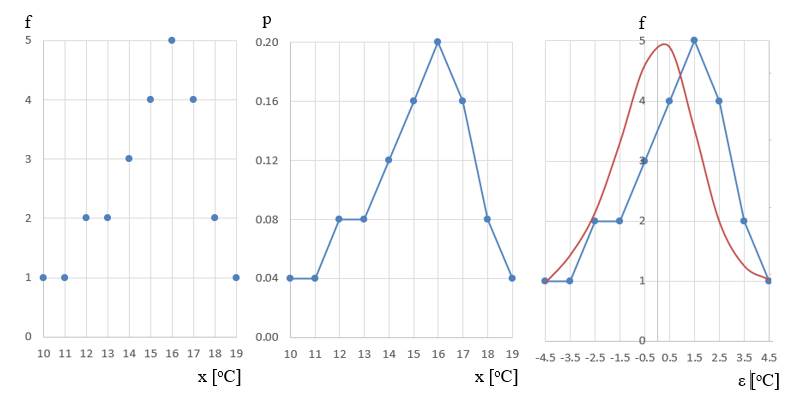
d e f

Fig. 2.7 Grafice ale frecvențelor variabilelor, probabilităților variabilelor și frecvențelor erorilor: a, b, c – teoretice; d, e, f – personalizate

Pentru realizarea de studii probabilistice/statistice curba frecvenţelor erorilor (ε_i = x_i – m) variabilelor aleatorii în raport cu media (linia frântă albastră din fig 2.7,f) se asociază (compară) cu o curbă (funcție, lege) de referință (teoretică), marcată cu roșu. Astfel, deoarece distribuția valorilor măsurate pe un eșantion nu se cunoaște, aceasta se va putea asocia (compara) cu distribuții probabilistice predefinite (de referință). 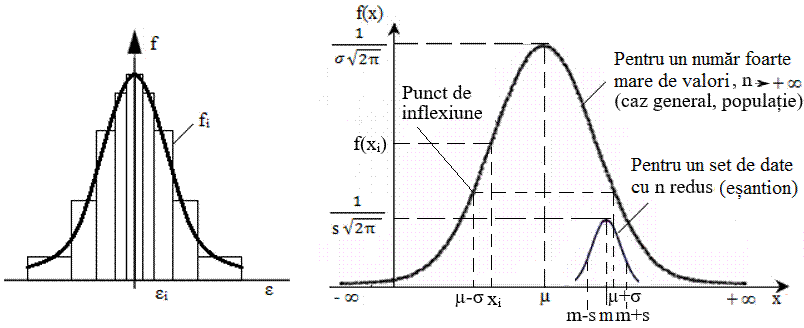De obicei, în studiile practice se folosește curba de distribuție de referință, asimilată cu cloptul lui Gauss (fig.2.8). În cazul numărului măsurătorilor foarte mare (n → ∞), erorile cu valorile mari (fig. 2.8,b) au o probabilitate mică de apariţie faţă de erorile mici care sunt mult mai probabile.

2.4.2 Distribuții (repartiții, legi) probabilistice teoretice

2.4.2.1 Distribuția normală (Gauss)

În cazul general, distribuția Gauss a unei variabile aleatoare continue, are la bază funcţia (legea) de distribuție normală (Normal Distribution),

f(x) = ,

în care, μ reprezintă media, σ – abaterea standard a variabilei aleatoare x ϵ (- ∞, + ∞). Această funcție (fig. 2.8,b), numită și distribuție gaussiană, este caracteristică volumelor mari de valori (măsurători), n → ∞, care în practica studiilor experimentele nu pot fi determinate ca valori numerice, fiind considerată doar ca funcție (lege) tendinţă (ţintă, referinţă, caz general, populație).

De obicei, datele obținute prin măsurători (inclusiv, din inginerie), din considerente practice, sunt asociate unei variabile aleatoare cu număr (n) de valori redus, de obicei, asociat unui eșantion. În acest caz (fig. 2.8,b), funcția de repartiție normală, devine,

f(x) = ,

unde, m reprezintă media, s - abaterea standard, asociate unui eșantion cu variabila aleatoare x cu n valori.

a b

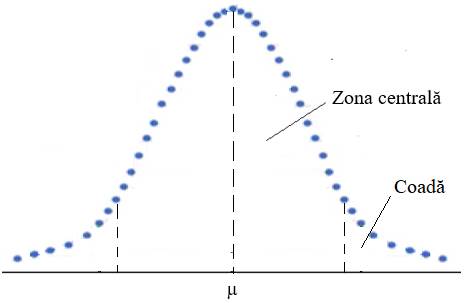
Fig. 2.8 Distribuția normală: a – asociată frecvenței erorilor; b – asociată funcției distribuție normală (Gauss)

Proprietăți ale distribuției normale (Gauss):

- este simetrică în jurul mediei aritmetice (µ sau m) și porțiunile extreme (numite și cozi) tind la infinit (pentru cazul general, n → ∞); de fiecare parte a mediei se află jumătate din valorile distribuției;

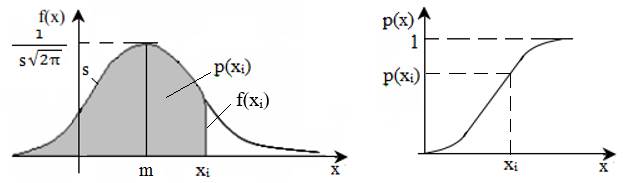
- valoarea f(x_i) reprezintă ordonata corespunzătoare valorii x_i cu maximul, f(µ) = ; f(m) = ; cele mai multe valori sunt grupate în jurul mediei (µ sau m);

- aria totală de sub curbă, reprezintă funcția de repartiție sau densitate de probabilitate (cumulată) (Cumulative Distribution Function, CDF) corespunzătore valorii x_i, se determină, pentru populație, cu relaţia (fig. 2.9,b),

p(x_i) = p(x < x_i) = =

sau, pentru eșantion,

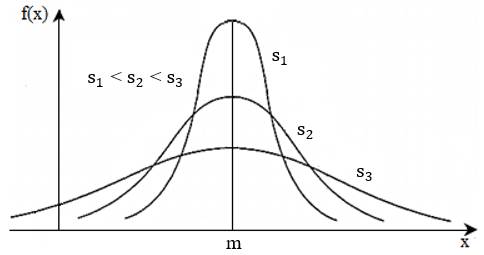
p(x_i) = p(x < x_i) = =,

cu valorile probabilităților, p(x_i) ϵ [0,1]; valoarea maximă este este egală cu 1 arată că toate rezultatele (100%) sunt afectate de erori;

- pentru valori ale abaterii standard, s, mici graficul este mai puțin împrăştiat (fig. 2.10).

a b

Fig. 2.9 : Funcția de repartiție (densitatea de probabilitate): a – asociată cu aria de sub curba de distribuție; b – asociată probablilității

Fig. 2.10 Forme ale curbelor de distribuție normală

Pentru determinarea valorilor funcțiilor f(x_i) și p(x_i) se pot utiliza tabele sintetice cu valori predefinite sau funcția Excel NORM.DIST (v.subcap.2.5.3.6).

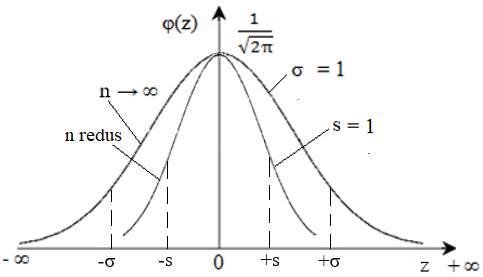
2.4.2.2 Distribuția normală standard

În studiile experimentale ale fenomenelor/proceselor fizice cu măsurători, majoritatea datelor se încadrează în distribuţia normală. Dar, deoarece, deseori se impune compararea/analizarea statistică a datelor asociate aceluiași fenomen/proces fizic dar exprimate diferit (de ex. unități de măsură diferite), se poate apela la distribuţia normală standard care conduce la noi indicatori statistici facili privitor la interpretarea rezultatelor.

Prin schimbarea variabilei x în variabila adimensională, z = sau z = , numită scor sau punctaj, distribuția normală (Gauss), devine distribuţia normală standard (numită și distribuția z, fig. 2.11) definită de de relația,

φ(z) = .

Astfel, în urma transformării se obțin: μ = 0, σ = 1, pentru cazul general (populație), n →∞, și m = 0, s = 1, pentru eșantion, n finit. Valorile scorului z se pot determina din tabele sintetice cu valori predefinite sau prin calcul numeric, de ex. folosind funcția statistică Excel STANDARDIZE (v.subcap.2.5.3.6).

Proprietăți ale distribuției normale standard:

- păstrează forma distribuției inițiale (deoarece, transformarea este liniară);

- prin standardizare valorile variabilei aleatorii devin adimensionale și deci, se pot face comparații statistice ale datelor asociate diverselor eșantioane;

- z = 0, induce valoare nulă a mediei (m sau μ); z < 0, valoarea este mai mică ca media; z > 0, valoarea este mai mare ca media.

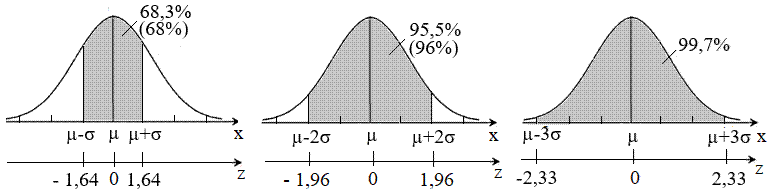
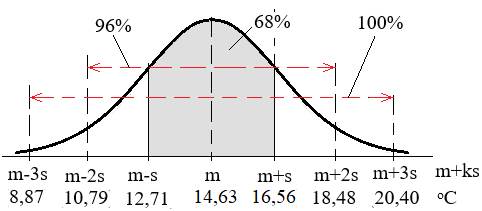
Fig. 2.11 Distribuții normale standard pentru populație și eșantion

Valoarile funcţiei densitate de probabilitate asociată distribuției normală standard pentru populație (n → ∞) precum și pentru eșantion (n finit redus) se pot obține din tabele sintetice cu valori predefinite sau prin calcul numeric, de ex. folosind funcțiile statistice Excel NORM.DIST și, respectiv, NORM.S.DIST (v.subcap.2.5.3.6). Astfel, se pot determina uşor aprecieri probabilistice privind: procentul (probabilitatea) valorilor unui set de date care se află sub o anumită valoare standard z sau procentul valorilor setului care se află într-un interval z.

Cunoașterea valorilor parametrilor μ și σ (uneori, chiar teoretic), pentru cazul unei populații (n → ∞) permite, pe de-o parte, determinarea probabilității pe care o are variabilă de a se găsi într-un interval oarecare sau, pe de altă parte, determinatrea intervalului în care se poate găsi o variabilă cu o probabilitate impusă numită nivel (prag) de încredere (p), egală cu aria de sub funcţia de distribuție normală, α = 1- p, de obicei, numit nivel (prag) de semnificaţie (de risc). Astfel, s-au definit intervale de încredere, [µ - kσ, µ + kσ], centrate în raport cu media µ, pentru care nivelul de încredere are probabilitatea p_k și nivelul de semnificație (risc), α_k = 1 - p_k. În practica studiilor statistice se folosesc, cu precădere, trei variante (valori) ale factorului k = 1, 2, 3 cărora corespund intervalele de încredere [µ - σ, µ + σ], [µ - 2σ, µ + 2σ] sau [µ - 3σ, µ + 3σ], cu nivelurile de încredere p₁ = 0,683 (68,3%), p₂ = 0,955 (95,5%) sau, respectiv, p₃ = 0,997 (99,7%) și nivelurile de semnificație (de risc) 0,317 (31,7%), 0,045 (4,5%) sau, respectiv, 0,03 (3%). Se observă că in intervalul [- µ - 3σ, µ + 3σ] se pot identifica (găsi) aproape toate valorile variabilei x.

a b c

Fig. 2.12 Intervale și niveluri (praguri) de încredere: a – [µ - σ, µ + σ], 0,683 (68,3%); b – [µ - 2σ, µ + 2σ], 0,955 (95,5%) ; c – [µ - 3σ, µ + 3σ], 0,997 (99,7%)

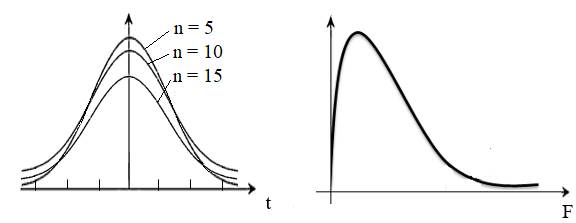
Obs. Funcțiile Gauss (nestandard și standard) sunt folosite frecvent în inginerie deoarece în majoritatea proceselor de măsurare, inevitabil, intervin erori, care prelucrate prin calcule specifice pot estima (prognoza) probabilitatea (riscul) de indentificare a unei valori date într-un domeniu impus.

2.4.2.3 Distribuția t (Student)

Distribuția t se folosește pentru reprezentarea erorilor aleatoare în cazul unui număr mic de măsurători, n < 30 când distribuția Gauss nu este relevantă. Aceasta descrie o familie de distribuții dependente de mărimea eșantioanelor (fig. 2.13,a). Pentru un eșantion ce conține mai mult de 30 măsurători, distribuția t devine identică cu distribuția z .

a b

Fig. 2.13 Alte distribuții probabilistice: a – Student; b – Fischer

Valorile variabilei distribției student se dau tabelar în funcție de nivelul de încredere și numărul de măsurători (grade de libertate) sau se pot calcula cu funcții statistice.

Obs. Distribuția t se poate folosi și pentru testarea diferenței dintre eșantioane la schimbarea mediului de măsurare. Prin schimbarea unei condiții se poate vedea dacă aceasta are influență asupra mărimilor măsuate. Astfel, pentru două eșantioane cu medii și abateri abateri standard diferite se pot rezolva teste statistice t, caută să se infirme sau nu o ipoteza preliminară (de nul) cu un anumit nivel de probabilitate impus (v.subcap.2.5.5.6.2).

2.4.2.4 Distribuția F (Fischer)

Distribuția Fisher (fig. 2.13,b) definită pe intervalul [0, +∞) poate descrie comportarea raportului a două variabile aleatorii. Variabilele de tip Fisher depind de numărul măsurătorilor (gradelor de libertate) (v.subcap. 2.5.5.6.6).

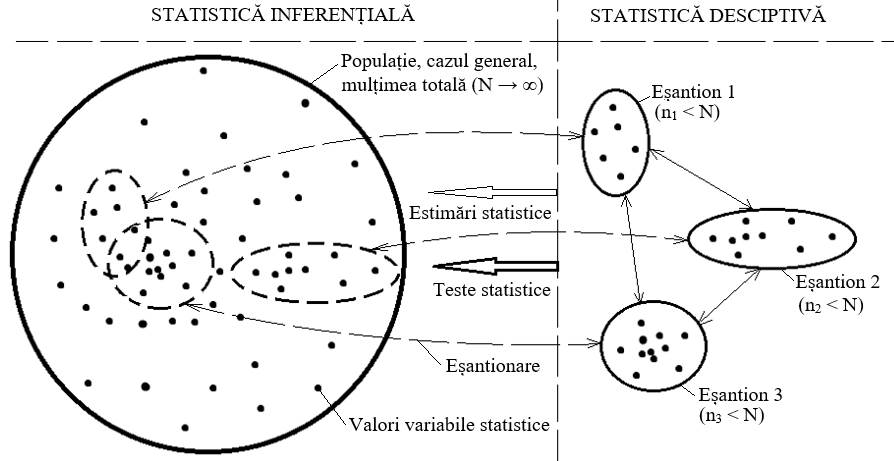
2.5 PRELUCRAREA STATISTICĂ A DATELOR EXPERIMENTALE

2.5.1 Aspecte generale

Statistica este știință care se ocupă cu achiziția (culegerea), prelucrarea și interpretarea datelor, cu precădere aleatorii, bazat pe o colecţie de metode, tehnici probabilistice, asociate unor entităţi, obiecte, sisteme sau fenomene/procese în scopul descrierii comportării acestora și al determinării legilor care le guvernează.

Statistica descriptivă presupune determinarea unor indicatori statistici care, pe lângă faptul că dau informaţii generale (sintetice) despre date, stau la baza analizelor statistice privind structura și organizarea datelor, cu precădere, asociate eșantioanelor (fig. 2.14). Analizele statistice descriptive, bazate pe teorii probabilistice, sintetizate în indicatori statistici caracteristici, dau cercetătorului posibilitatea de a preciza localizarea și variabilitatea (împrăştierea) datelor experimentale asociate unui fenomen/proces.

Fig. 2.14 Tipuri de studii statistice

Statistica inferenţială presupune studii de bazate, de obicei, pe informaţii obținute cu statistica descriptivă (fig. 2.14), pentru a lua decizii și trage concluzii privitoare la populații, cazuri generale (teoretice) bazate pe date cu numere mari de valori. Spre deosebire de statisticile descriptive, care includ metode aplicate unui set de date, cu precădere, asociate unuia sau mai multor eșantioane (submulțimi ale cazului general, populației), statisticile inferențiale urmăresc prin metode specifice (teste statistice) deducerea și estimarea unor parametri și/sau legi asociate cazului general (populației). Analizele (testele) statistice inferențiale, de obicei, se fac în continuarea analizelor descriptive bazate pe experimente, și au ca obiectiv obținerea de valori și/sau concluzii privind aprecierea generală a comportării fenomenului/procesului.

Analizele statistice descriptive și inferențiale ale datelor experimentale, în cadrul acestei lucrări, se fac cu funcții statistice ale pachetului software Microsoft Excel grupate în modulul Data Analysis care se activează de utilizator (v.Ghid.Excel.02).

2.5.2 Variabile statistice

Variabila statistică este o submulțime de valori aleatoare care, de obicei în inginerie, reprezintă prin atribute (greutate, culoare, mărime, presiune etc.)caracteristici specifice ale obiectelor și/sau fenomenelor/proceselor fizice. Aceasta poate avea un număr finit de valori numerice (cantitative) sau alfanumerice (calitative) care se asociază (tab. 2.1), de obicei, unui eșantion. Valorile cantitative, frecvent, reprezintă mărimi cu unități de măsură asociate fenomenelor/proceselor fizice cercetate, de obicei, unităţi naturale ale unor mărimi fizice (masa (kg), volumul (m³), lungimea (m), forţa (N) etc. În general, variabilele statistice pot fi încadrate în două grupe: calitative și cantitative (tab. 2.1)

Variabile calitative (categoriale), de obicei, alfanumerice nu se determină prin măsurare; în practică acestora li se pot asocia și numere cu care nu se vor efectua operții algebrice; cuantificarea valorilor calitative, de obicei, se face face procentual (%).

Variabile cantitative sunt asociate unor caracteristici (parametri) măsurabile, de obicei, sub forma unui set de valori numerice care se pot ordona; variabile cantitative continue se transformă în variabile calitative prin împărțirea în clase (conform unor reguli convenționale) ex. intrervalului 0 … 20 se asociază valoarea ”bun”; 20 … 50, „foarte bun”; 50 … 80, excelent” etc.

Tab. 2.1 Tipuri de variabile statistice
Grupa variabilei	Tipul variabilei	Descriere	Exemple
Calitative (categoriale)	Nominale	Nu poate fi ordonată (valorile se exclud reciproc)	Bărbat, femeie, roșu etc.
	Ordinale	Valorile se pot ierarhiza (ordona)	Bun, foarte bun, excelent etc.
	Binare	Au valori dihotomice	Alb/negru, cald/rece clar/neclar etc.
Cantitative	Continue	Pot lua o infinitate de valori reale (de ex. temperatura, presiunea etc.)	Temperatura, presiunea, forța etc.
	Discrete	Valori numere întregi (naturale)	Numărul de obiecte, numărul de culori etc.

Obs. Tipul variabilelor statistice se alege corelat cu tipul analizelor și testelor statistice ce se vor realiza în continuare.

2.5.3 Elemente de statistică descriptivă

2.5.3.1 Indicatori statistici descriptvi, generalități

Pentru studii statistice a grupării valorilor și/ sau erorilor se impune definirea unor indicatori care descriu calitativ și/sau cantitativ dispersia (împrăștiera) valorilor variabilei aleatorii în jurul unei valori medii, de obicei, media aritmetică.

Indicatorii statistici (tab. 2.2) se reprezintă prin valori numerice ce permit caracterizarea din punct de vedere cantitativ și/sau calitativ a unuia sau mai multe seturi de date asociate unui obiect, fenomen, proces sau sistem fizic; în plus, aceștia pot descrie și evoluţia în funcţie de condiţiile concrete de experimentare precum şi compararea seturilor de măsurători diferite.

Tab. 2.2 Tipuri de indicatori statistici descriptivi
Criteriul de clasificare	Tipul indicatorului	Descriere
Scopul urmărit	De comparare	Sunt utilizați pentru identificarea modificărilor intervenite ca structură sau nivel de evoluție, pornind de variabilitatea datelor
	De sinteză	Se descriu printr-o expresie numerică care devine tipică şi esenţială pentru mai multe seturi de date
	De estimare	Prin intermediul unor funcţii de estimare se fac predicții ale tendinţei unui fenomen sau proces, variabil
	De verificare	Pentru evaluarea influenţelor datorate unor factori interni şi externi, deoarece fenomenele/procesele sunt diverse şi variabile
	De informare	Indică valori care provin direct din datele studiate și care, uneori, stau la baza adoptării unor prelucrări ulterioare
Volumul valorilor	Individual	Se referă la o singură valoare a unei variabile (ex. probabilitatea de apariție a unei valori impusă)
	Global	Sintetizează informații despre mai multe valori, submulțimi sau seturi de date (ex. media aritmetică, dispersia etc.)
Tipul valorilor	Absolut	Variabilele au unități de măsură. Ex.
	Relativ	Adimensionali folosiți, cu precădere, pentru compararea parametrilor caracteristici ai diverselor seturi de date
Funcțiile de îndeplinit	Al tendinței centrale	Indicatorii de medie se referă la valorile "de mijloc" (centrale) ale unui set de date. Acești indicatori exprimă (estimează) în mod generalizat şi sintetic în câte o singură valoare numerică tendinţa de dispunere a valorilor unei set de măsurărtori (ex. media aritmetică, mediana, modul)
	De poziționare	Datele obținute prin măsurători sunt distribuite neuniform în cadrul domeniului limitat de valorile extreme (maxim și minim). Acești indicatori descriu poziționarea datelor în cadrul unor subdomenii ale domeniului măsurătorilor (ex. percentile, cuartile etc.)
	Al formei distribuției	Sunt utilizați pentru compararea, cuantificabil, a distribuției efective a valorilor unui set de măsurători cu distribuții teoretice (ex. asimetria, boltirea etc.)
	De împrăștiere	Valorile măsurate se abat de la tendinţa centrală (de medie) consecință a diverselor influenţe exterioare procesului de măsurare. De cele mai multe ori este important de cunoscut cât de "aproape" sau de "departe" sunt valorile măsurătorilor faţă de zona centrală a dispersiei datelor (ex. dispersia (varianța), abaterea standard etc.)
	De abatere (eroare)	Cuantifiă abaterile valorilor statistice determinate (ex. eroarea standard a mediei, coeficientul de variație)
	De încredere (risc)	Determinarea valorilor sau intervalelor care arată cu o probabilitate impusă apartenența unei valori date (ex. intervalul de încredere, nivelul de încredere, nivelul de semnificație etc.)
	De corelare	Caracterizează cantitativ interdependența a două mărimi statistice comparabile, asociate datelor care aparţin obligatoriu unuia şi aceluiaşi obiect/fenomen/proces (coeficientul de covarianță, coeficentul de corelație, matricea de covarianță)

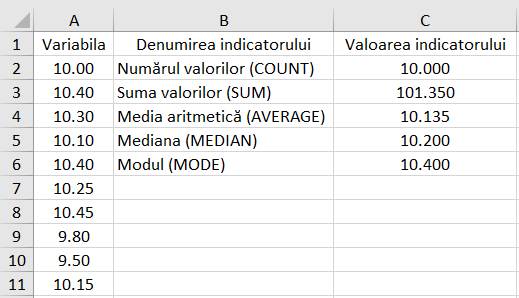
2.5.3.2 Indicatori statistici ai tendinței centrale (de medie): Media, Mediana, Modul

Ap.2.01 Determinarea indicatorilor tendinței centrale pentru un set de măsurători (variabila x) cu n = 10 valori (coloana A din fig. 2.15) (Ghid.Ap.2.01)

Semnificații

Maximul/Minimul (Max/Min) valorilor unui set de date se determină cu funcțiile Excel MAX/MIN. Amplitudinea (Amp) valorilor unui set de date indică domeniul maxim de răspândire a valorilor setului și se determină cu relația, Amp = Max-Min. Numărul valorilor setului de date (n) se determină cu funcția Excel, COUNT. Suma valorilor setului de date (Sum) se determină cu funcția Excel, SUM. Media (aritmetică) se determină cu relația, m = pentru eșantioane (cu n redus) sau µ = pentru populații (cu n foarte mare), unde xi reprezintă valorile valoarea variabilei. Se determină cu funcția Excel, AVERAGE. Mediana (Med) reprezintă valoarea centrală ce împarte un set de date ordonat în două submulţimi (crescătoare, respectiv, descrescătoare); se determină cu funcția Excel, MEDIAN. Modul (Mod) reprezintă valoarea care înregistrează cea mai mare frecvenţă de apariţie; se determină cu funcția Excel, MODE (fig. 2.16)

Interpretări

Media (aritmetică) a valorilor unei variabile asociată unui eșantion este cel mai utilizat indicator pentru estimarea valorilor unor parametri ai populației (cazului general); are dezavantajul că în cazul apariției unori valori extreme (aberante) relativ îndepărtate față de valorea centrală conduce la estimări nereprezentative. Mediana împarte setul de date în două jumătăți (egale ca număr de valori), una conține valorile mai mici și cealaltă valori mai mari decât aceasta; în cazul numărului impar de valori, mediana este valoarea din mijlocul setului de date ordonat (valoare diferită de valorile variabilei), sau pentu cazul numărului par de valori este media aritmetică a valorilor setului de date ordonat (ex. pentru setul de date par {1, 2, 3, 4, 5} mediana este 3 și pentru setul de date impar {1, 2, 3, 4} este 2,5). Valoarea medianei mult diferită de valoarea mediei evidențiază existența unor valori extreme (aberante) care conduc la valori ale mediei nereprezentative (ex. pentru setul de date {1, 3, 5, 7, 9, 11, 130}, mediana este 7 și media 23,7, arată existența valorii extreme 130 care dacă ar fi eliminată conduce la mediana, șase, egală cu media). Modul evidențierea tipului curbei de distribuție: cu un vârf, unimodală; cu două vârfuri, bimodală (fig. 2.15); dacă nicio valoare nu are frecvența mai mare ca unu setul de date nu are mod. În fig. 2.17 se prezintă cazuri posibile privind valorile indicatorilor tendinței centrale: fig. 2.17,a - media, mediana și modul sunt egale conduce la distribuția simetrică; fig. 2.17,b - media, mediana și modul sunt crescătoare (fig. 2.17) conduce la distribuția asimetrică spre stânga; fig. 2.17,c – modul, media și mediana sunt descrescătoare conduce la distribuția asimetrică spre dreapta. Obs. - Dacă mai multe valori numerice au aceeași frecvență maximă (modul) se spune că setul de date este multimodal. - Mediana este egală cu perceptila P50 (valoarea până la care se găsesc 50% dintre valori) și cu cuartila Q2 (v.subcap. 2.5.3.3)

Fig. 2.15 Tabel cu valori ale datelor și indicatorilor Fig. 2.16 Graficul funcției MODE

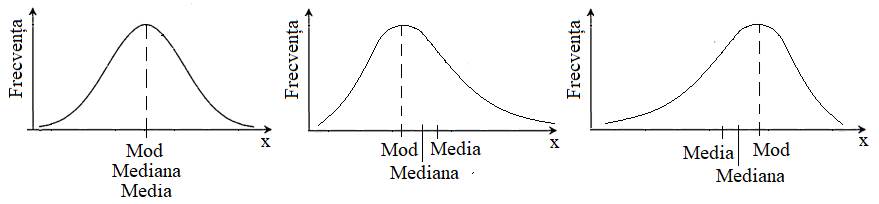
a b c

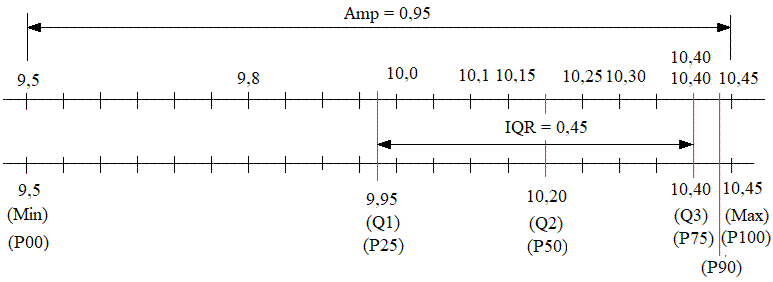
Fig. 2.17 Variante posibile ale indicatorilor de medie: a – valori identice; b – valori crescătoare în ordine Mod, Mediana, Media; b – valori crescătoare în ordine Media, Mediana, Mod

2.5.3.3 Indicatori statistici de poziționare (localizare): Maximul/Minimul, Amplitudininea (Range), Caurtile, Percentile

Ap.2.02 Determinarea a indicatorilor de poziționare pentru un set de măsurători (variabila x) cu n = 10 valori (coloana A din fig. 2.18) (Ghid.Ap.2.02)

Semnificații

Indicatorii de poziționare oferă informații privind poziționarea (localizarea) valorii unei variabile asociată unui set de date. Maximul/minimul reprezintă valoarea maximă/minimă a valorilor unei variabile (fig. 2.18); funcții Excel MAX/MIN sau DATA ANALYSIS (Ghid.Excel.02). Amplitudininea (range), diferența dintre cea mai mare (maximul) și cea mai mică (minimul) valoare a unei variabile. Caurtilele sunt sintetizate în 3 valori limită (Q1, Q2, Q3) care reprezintă valorile limită până la care se găsesc 25%, 50%, respectiv, 75% din valorile unui set de date; cele 3 valori limită, Q1, Q2 și Q3, împart setul de valori în câte două grupe (subintervale) care conțin: 25% și 75%, 50% și 50%, 75% și 25% din valorile acestuia; se determină cu funcțiile Excel QUARTILE.INC (include mediana) sau QUARTILE.ESC (exclude mediana). Intervalul intercuartil (InterQuartile Range, IQR), Q3-Q1, reprezintă domeiniul care conține 50% din valorile unui set de date (fig. 2.20). Percentilele sunt valorile limită, P0, P1, P2, P3, … P100, care reprezintă valoarile până la care se găsesc 0%, 1%, 2%, 3% … respectiv, 100% din valorile unui set de date, ex. P80 indică o valoarea până la care se găsesc 80% din valorile setului de date; pe de altă parte, percentilele P1, P2, P3, … P99, împart setul ordonat de valori în 100 de grupe (subintervale) egale; se determină cu funcțiile Excel QUARTILE.INC (include mediana) sau QUARTILE.ESC (exclude mediana). Obs. Corespondențe (fig. 2.19): P0 = Minim, P25 = Q1; P50 = Q2 (corespunde cu mediana), P75= Q3, P100 = Maxim (fig. 2.19)

Interpretări

Percentile și cuartile sunt asociate valorilor unui set de date și evidențiază procentual poziționarea (localizarea) valorilor în raport cu limite impuse (fig. 2.18, fig. 2.19); de ex. pentru setul de valori din fig. 2.18: valorile Q1 și P25 (egale cu 10,025) indică că 25% din valori sunt mai mici decât 10,025 și 75% din acestea, mai mari; valorile Q2 și P50 (egale cu 10,200) indică că 50% din valori sunt mai mici decât 10,200 și 75% din acestea, mai mari; valorile Q3 și P75 (egale cu 10,375) indică că 25% din valori sunt mai mici decât 10,375 și 25% din acestea, mai mari. Ținând cont de valorile de mai sus prin scăderea limitelor se pot determina poziționarea (localizarea) în subintervale: de ex. pentru setul de valori din fig. 2.18 și 2.19,b în intervalele: (Min, Q1) ((9,500; 10,025)), (Q1, Q2) ((10,025; 10,200)), (Q2, Q3) ((10,200; 10,375)), (Q3, Max) ((10,375; 10,450)) se găsesc 2 valori (25%); în intervalele (Min, Q2) ((9,500; 10,200)), (Q2, Max) ((10,02; 10,450)), (Q1, Q3) ((10,200; 10,375)) se găsesc 4 valori (50%). Dacă se dorește determinarea poziționării (localizării) valorilor în raport cu alte limite corespunzătoare procentelor 0%, 25%, 50%, 75%, 100% se pot utilza percentilele; de ex. pentru setul de valori din fig. 2.19: valorea P90 (egală cu 10,405) indică că 90% din valori sunt mai mici decât 10,405 și 10% din acestea, mai mari; în intervalele [P50, P90] ([10,200; 10,405]) se găsesc 40% din valorile setului de date. IQR = 0,350, indică că 50% din valorile variabilei sunt în domeniul 0,350 centrat în intervalul [Q1, Q3] În fig. 2.19,b,c sunt prezentate localiz[rile (poziționările) valorilor generate cu funcțiile Excel QUARTILE. INC, PERCENTILE.INC, respectiv, QUARTILE. ESC, PERCENTILE.ESC

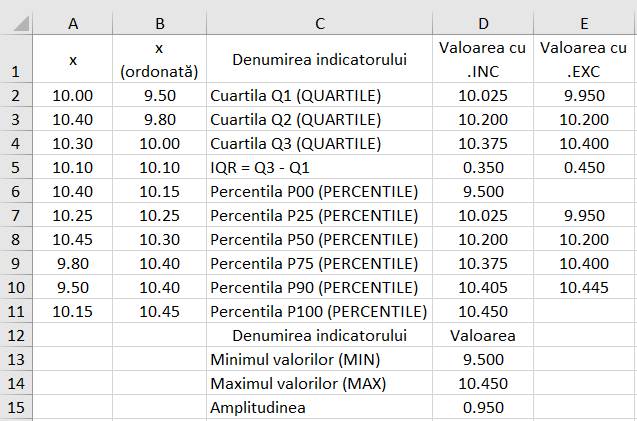
Fig. 2.18 Tabelul cu valori ale datelor și indicatorilor

a

b

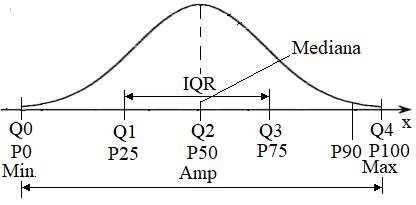
c

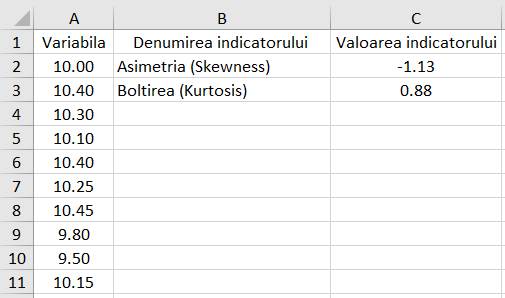
Fig. 2.19 Localizări ale valorilor generate cu funcțiile Excel, QUARTILE și PERCENTILE: a – în raport cu indicatorii de medie la general; b, c – în raport cu indicatorii de medie personalizați

2.5.3.4 Indicatori statistici ai formei distribuției: Asimetria (skewness), Boltirea (kurtosis)

Ap.2.03 Determinarea indicatorilor formei distribuției pentru un set de măsurători (variabila x) cu n = 10 valori (coloana A din fig. 2.20) (Ghid.Ap.2.03)

Semnificații

Asimetria (Skewnes, Skew) evidențiază abaterea formei distribuției unui set de date (fig. 2.21,b,c) în raport cu o distribuție normală în jurul mediei (fig. a); funcţia Excel: SKEW. Boltirea (Kurtosis) indică gradul de aplatisare (ascuțire) a distribuției unui set de date fig. 2.22,b,c) în raport cu o distribuție normală în jurul mediei (fig. a); funcţia Excel: KURT

Interpretări

Asimetria cuantificabilă prin coeficientul de asimetrie (Skew) cu valoarea 0 arată că distribuția este normală (simetrică, fig. 2.21,a); valorile pozitive ale coeficientului de asimetrie Skew indică distribuție asimetrică pozitiv, cu coadă spre dreapta (fig. 2.21,c); pentru valori negative (fig. 2.21), distribuția este asimetrică negativ, cu coadă spre stânga (fig. 2.21,b); valori mai mici sau mai mari ca unu indică asimetrii negative, respectiv, pozitive pronunțate. Tipul și dimensiunea asimetriei este determinat și de valoarea diferenței dintre medie și mediană (v. fig. 2.17): mediana-media = 0, implică asimetrie zero; mediana-media < 0, asimetrie negativă; mediana-media > 0, asimetrie pozitivă. Boltirea corespunzătoare coeficientului de boltire (Kurt) egal cu valoarea zero indică o distibutie normală (mezocurtică, fig.2.22,a) spre deosebire de cele negative cu distribuție mai aplatisată (platicurtică, fig.2.22,c) sau de cele pozitive cu distribuție mai ascuțită (leptocurtică, fig.2.22,b)

Fig. 2.20 Tabel cu valori ale datelor și indicatorilor

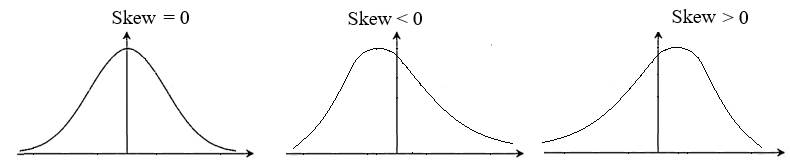
a b c

Fig. 2.21 Forme de poziționare a distribuției datelor în raport cu distribuția normală în jurul mediei: a – simetrică; b – asimetrică negativ; c – asimetrică pozitiv

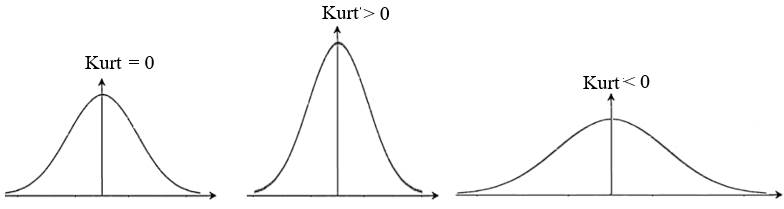
a b c

Fig. 2.22 Forme privind ascuțirea (aplatisarea) distribuției datelor în raport cu distribuția normală în jurul mediei: a – nedeformată; b – ascuțită; c – aplatisată

2.5.3.5 Indicatori statistici de dipsersie (împrăștiere): Dispersia (variance), Abaterea standard (standard deviation), Coieficientul de variație, Eroarea standard

Ap.2.04 Determinarea indicatorilor de dispersie (împrăștiere) pentru un set de măsurători (variabila x) cu n = 10 valori (coloana A din fig. 2.23) (Ghid.Ap.2.04)

Semnificații

Dispersia (Variance, VAR) este media aritmetică a pătratelor abaterilor valorilor unui set de date faţă de medie, și se determină cu relațiile: σ^2= /N, unde, N reprezintă numărul de valori ale populației (cazul general) cu N foarte mare (N → ∞), μ – media (aritmetică); s^2= /(n-1), unde, n reprezintă numărul de valori ale unui eșantion (n are valoare mică), (n-1) – numărul gradelor de libertate. Funcții Excel: VAR.P, pentru cazurile cu numere de valori foarte mari (n → ∞); VAR.S sau VAR, pentru cazurile cu numere de valori reduse (eșantioane). Dispersia are dezavantajul că valorile se reprezintă conform unităţilor de măsură ridicate la pătrat, şi are, în general, valori mari comparativ cu abatereile individuale de la medie (xi – m). Astfel, deseori, se foloseşte un alt indicator, numit abatere standard care se exprimă ca radical din dispersie. Abaterea standard (Standard Deviation, SD) se determină cu relațiile: σ = , pentru populații, și s = , pentru eșantioane. Funcții Excel: SDDEV.P, pentru cazurile cu numere de valori foarte mari (n → ∞); STDEV.S sau STDEP, pentru cazurile cu numere de valori reduse (eșantioane). Acest indicator se exprimă cu aceeaşi unitate de măsură ca şi valorile setului de date şi are o valoare comparabilă cu abaterile individuale de la medie. Coeficientul de variație (CV), definit ca raport dintre abaterea standard şi medie (numai pentru cazurile cu media diferită de 0), CV = σ/µ sau CV = s/m, de obicei, este exprimat în procente. Eroarea Standard (ES) se determină cu relația, ES = s/, și reprezintă o estimare a abaterii mediei unui eșantion (numărul de valori n redus) față de media populației statistice (n → ∞), pentru care ES → 0

Interpretări

Indicatorii de dispersie (împrăștiere) indică sintetic (global) gruparea (împrăștierea) valorilor setului de date în jurul mediei (fig. 2.24); aceștia permit, pe de-o parte, aprecierea gradului de omogenitate al valorilor unui set de date, precum şi, pe de altă parte, dacă media este reprezentativă (cu cât se abat valorile unui set de date faţă de medie); se pot întâlni situații în practică când valorile setului de date nu sunt în jurul mediei se situează preponderent în stânga şi/sau dreapta (fig. 2.24,c), departe de medie, evidențiindu-se un grad de împrăștiere ridicat spre deosebire de cazul din fig. 2.24,c cu împrăștiere redusă valorile fiind apropiate de medie. Abaterea standard este idicatorul de dispersie cuantificabil (cu aceași unitate de măsură cu media) ce atașază mediei, Media ± SD, fiind o măsură a împrăștierii valorilor unei variabile în jurul mediei; aspecte comparative: cu cât valoarea abaterii standard este mai mare/mică cu atât dispersia (împăștierea) valorilor setului în jurul mediei este mai mare/mică (largă/îngustă); la medii aproximativ egale, este mai împrăştiat setul cu abaterea standard (dispersia) mai mare; la dispersii aproximativ egale, este mai împrăştiat setul cu media mai mică. Coeficientul de variație reprezintă o măsură adimensională a împrăştierii datelor în raport cu media; cu cât valoarea CV este mai apropiată de zero, cu atât dipsersia este mai bună (mulţimea valorilor este mai omogenă), media având un grad ridicat de reprezentativitate; cu cât valoarea sa este mai departe de zero cu atât dispersia este mai slabă (mulţimea este mai eterogenă), iar media are un nivel de semnificaţie mai scăzut; CV este folosit și pentru compararea îmrăștierilor valorilor a două seturi de date în cazurile în care mediile şi abaterile standard sunt mult diferite şi abaterile standard nu pot să indice aspecte relevante; CV este cel mai fidel indicator al împrăştierii seturilor de date, fiind cu atât mai fidel cu cât mediile sunt mai depărtate de zero Obs. În practică, valori ale CV mai mici ca 0,33…0,35 indică un grad acceptabil de reprezentativitate al mediei și pentru valori mai mari se poate considera valoarea ca fiind nereprezentativă. Eroarea standard (ES) a mediei evidenţiază cu cât este în eroare cercetătorul determinând parametri statistici pentru un eşantion faţă de rezultatele pe care le-ar fi obṭinut pentru mulţimea totală (populația statistică) cu ES → 0. Valori mici (apropiate de zero) ale ES indică abateri acceptabile ale rezultatelor statistice obținute bazat pe setul de date asociat unui eșantion. Deci, eroarea standard a mediei ca indicator global de dispersie arată și împrăștierea mediilor eșantioanelor în jurul mediei populației.

Fig. 2.23 Tabel cu valori ale datelor și indicatorilor

a b c

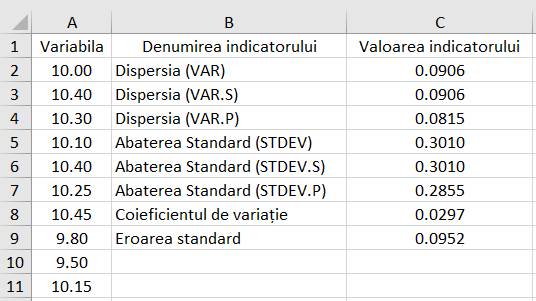
Fig. 2.24 Forme de împrăștiere (grupare) a datelor în jurul mediei: a – apropiată de medie; b – preponderent în dreapta; c – depărtată de medie

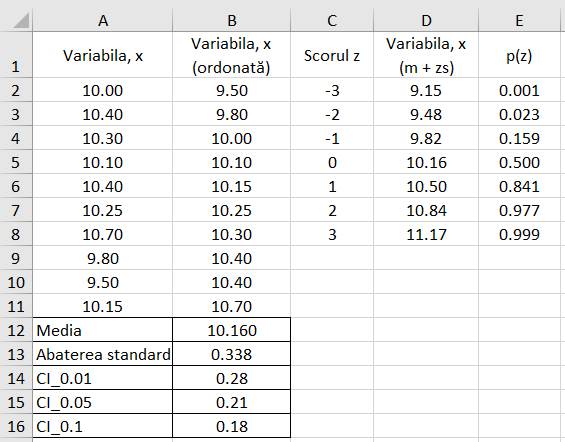
2.5.3.6 Indicatori statistici de probabilitate: Transformata z, Densitatea de probabilitate (probabilitatea cumulată), Scorul z, Intervalul de încredere

Ap.2.05 Determinarea indicatorilor de probabilitate pentru un set de măsurători (variabila x) cu n = 10 valori (coloana A din fig. 2.25) (Ghid.Ap.2.05)

Semnificații

Transformata z se obține în urma schimbării de variabilă, z = , pentru populații sau z = , pentru eșantioane, asociată funcției distribuție normală (v. fig. 2.11, 2.26) pentru populație sau, respectiv, eșantion; funcţia Excel: STANDARDIZE. Scorul z exprimă poziția valorilor variabilei față de medie evaluată prin numere intregi de abateri standard (numerele de abateri standard peste/sub medie) (v. fig. 2.11, 2.26, 2.28, 2.29). Densitatea de probabilitate (Probabilitatea cumulată) se determină prin calculul ariei de sub funcția de repartiție normală de la -∞ la valoarea indicată (v. fig. 2.9, 2.27,a); funcţii Excel: NORM.DIST, pentru variabile x, sau NORM.S.DIST, pentru variabile z; Aceste funcții se pot aplica (selecta) în două variante: varianta cu argumentul TRUE, pentru calculul funcției densitate de probabilitae, CDF (Cumulative Distribution Function, fig. 2.27) și varianta cu argumentul FALSE, pentru calculul valorii punctuale a funcției de distribuție, PMF (Probability Mass Function; fig. 2.27,a; (v. Ghid.Ap.2.07) Valoarea variabilei corespunzătoare unei probabilități cumulate dată (problema inversă) presupune determinarea valorii unei variabile pornind de la o valoare a probabilității cumulată impusă, din intervalul [0,1] (fig. 2.27,b); funcţii Excel NORMINV, pentru variabila x sau NORM.S.INV, pentru variabila z. Intervalul de încredere (Confidence Interval, CI) Este asociat problemei de estimare a mediei unei populații statistice bazat pe un set de date asociat unui eșantion. Aprecierea (evaluarea) preciziei estimării mediei prin intermediul intervalului de încredere, [m – CIα, m + CIα], ale cărui limite sunt stabilte de parametrul CIα (Confidence Interval) corespunzător unui prag (grad, nivel) de încredere (siguranță) p impus, (de ex. p poate avea una din valorile: 0,99 (99%), 0,95 (0,95%), 0,9 (90%), uzual, p = 0,95 (95%)) dependent de α, pragul (gradul, nivelul) de semnificaţie (risc, nesiguranță), p = 1 – α, cu α ϵ {0,01; 0,05; 0,1} (uzual, α = 0,05). Parametrul CIα se determină cu o relație dependentă de α (pragul de semnificație), s (abaterea standard) și n (numărul de valori al eșantionului), de ex. CIα = zα/, unde zα reprezintă valoarea critică a scorului z, corespunzător pragului de încredere (p), respectiv, de semnificație α, impus (ex. în cazul distribuțiilor normale, pentru p = 0,95 (α = 0,05), zα = 1,96); funcția Excel, CONFIDENCE.

Interpretări

Transformata z se obține în urma procesului de standardizare a funcției cu variabila x (coloana C din fig.2.26). În fig. 2.25 și 2.26 se observă că valorile variabilei z ϵ [-1,95; 1,60], media m = 0 și abaterea standard s = 1. Această operație permite compararea a două distribuții normale (de obicei, când variabila este exprimată diferit (de ex. unități de măsură diferite, numărul de valori diferit) după ce se generează ambele transformate z. Obs. Transformata z nu modifică distribuția inițială. Transformata z a unei distributii normale conduce tot la o distribuție normală (teoretică), în timp ce o distributie z oarecare are forma distribuției valorilor inițiale, de obicei, de eșantion (fig. 2.26). Probabilitatea cumulată (problema directă) corespunzătoare unei valori a variabilei aleatorii x, de ex. x < 10,30 (coloana D din fig. 2.25, fig. 2.27) este p (x<10,3) = 0,661 (66,1% din valori sunt mai mici decât 10,3); folosind proprietățile de simetrie a distribuției normale, proabilitatea cumulată pentru x > 10,3 este p (x > 10,3) = 1 - p (x < 10,3) = 1 - 0,661 = 0,339 (33,9% din valori sunt mai mari decât 10,3) sau probabilitatea cumulată pe un interval, de ex. pentru [10,00 10,40] este p(x<10,40) - p(x<10,00) = 0,761 – 0,318 = 0,443 (44,3 % din valori sunt cuprine în intervalul [10,00 10,40]). Aceleași valori se obțin și pentru cazul în care probabilitatea cumulată se determină în raport cu variabila standard z (coloanele D și E sunt identice). Valoarea variabilei corespunzătoare unei probabilități cumulate dată (problema inversă) reprezintă limita (xi sau zi) a ariei de sub curba unei distribuții standard normale; de ex. valorii probabilității cumulată, 0,661, îi corespunde valoarea 10,3; prin aplicarea funcției NORM.INV respectiv, NORM.S.INV valorilor probabilităților din coloanele C, respectiv, F (fig. 2.25) se vor obține valorile variabilelor x și z (coloanele F și, respectiv, G sunt identice cu coloanele B și respectiv, C). Scorul z sau „scor standardizat” reprezintă numere întregi care exprimă, în multipli de abateri standard, „distanța” unei valori ale variabilei față de media distribuției din care face parte aceasta. În fig. 2.28 și 2.29 se evidențiază valorile întregi ale scorului z, ±1, ±2 (coloana D din fig.2.28) în corelație cu reprezentarea variabilei x în unități de abatere standard (s), m + (scorul z)s, (coloana C din fig.2.28); dacă scorul z este egal cu -1/-2/-3, acesta este cu una/două/trei abateri standard mai mic ca zero; dacă scorul z este egal cu +1/+2/+3, acesta este cu una/două/trei abateri standard mai mare ca zero; valori negative ale scorului z indică valori ale variabilei x < m, valori pozitive ale scorului z indică valori ale variabilei x > m. În urma calculului probabilităților cumulate (coloana E din fig. 2.28) și urmărind axa asociată acestora (fig. 2.29) se evidențiază următoarele situații: 15,9%, 50%, 84,1% din valorile variabilei x sunt mai mici decât 9,82, 10,16 (media), respectiv, 10,5; 13,6% din valori sunt în intervalele, [9,48; 9,82] și [10,5; 10,84]; 34,1% din valori sunt în intervalele, [9,82; 10,16] și [10,16; 10,5]; 68,2 % din valori sunt în intervalul, [m-s, m+s] = [9,82; 10,5]; 95,4% din valori sunt în intervalul, [m-2s, m+2s] = [9,48; 10,84] (fig. 2.30). Obs. Deoarece distributia normală reprezintă un model teoretic (cu ramurile spre infinit) care se consideră ca aproximează cu o eroare admisibilă statistic cele mai multe dintre distribuțiile reale (deseori, cvasinormale) obținute prin măsurători (totdeauna finite) conduc la valori probabilistice de estimare aproximative, și deci, pentru eșantioane de măsurare (cu valori măsurate reduse), pentru care distrubuția este deseori cvasinormală, practic, se pot considera intervalele [m − s, m + s], [m − 2s, m + 2s] și [m − 3s, m + 3s] în care se află aproximativ 90%, 95% și respectiv, 99 % din valorile setului de date (fig. 2.30,a,b,c) spre deosebire de cazul distribuției normală asociată populației statistice (număr cvasinfinit de valori) are valorile probabilitățiolor exacte (v. fig.2.12). Intervalul de încredere permite determinarea intervalului variabilei pentru care media este asigurată cu o probabilitate impusă (pragul de încredere p, pragul de risc 1-p) sau estimarea erorilor (abaterilor) limtă ale mediei cu o probabilitate impusă. În fig. 2.28 se prezintă valorile parametrului CIα pentru paragul de semnificație α cu valorile 0,01, 0,05, 0,1 (respectiv pragul de încredere p cu valorile 0,9, 0,95, 0,99 (90%, 95%, 99%)). Astfel, s-au obținut intervalele de încredere: [10,16-0,28; 10,135+0,28] = [9,88; 10,44]; [10,16-0,21; 10,16+0,21] = [9,95; 10,37] (fig. 2.29); [10,16-0,18; 10,16+0,18] = [9,98 10,34] care evidențiază că valoarea estimată a mediei (10,16) pentru populația statistică aparține acestor intervale cu probabilitatea de 90%, 95% sau respectiv, 99%. Obs. CIα se poate determina fără a cunoaște valaorea mediei

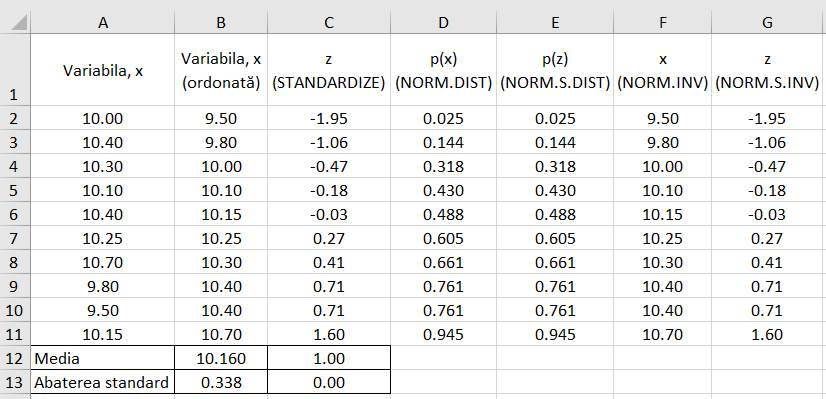
Fig. 2.25 Tabel cu valori ale datelor și indicatorilor

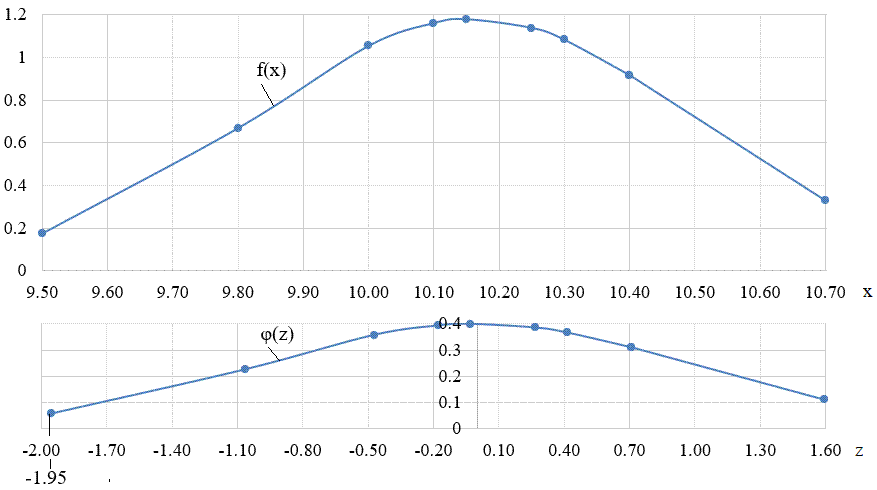
Fig. 2.26 Transformata φ(z) a funcției f(x)

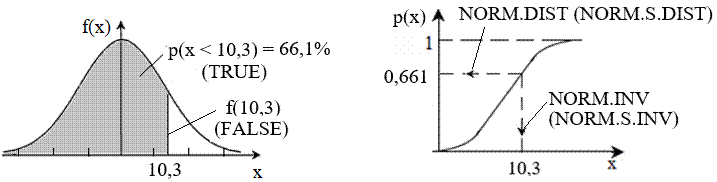
a b

Fig. 2.27 Funcții probabilistice: a – de repartiție cu densitatea cumulată (CDF) și punctuală (PMF); b – cu funcțiile densitate de probabilitate Excel, directă și inversă

Fig. 2.28 Tabel cu valori ale datelor și ale indicatorilor de probabilitate

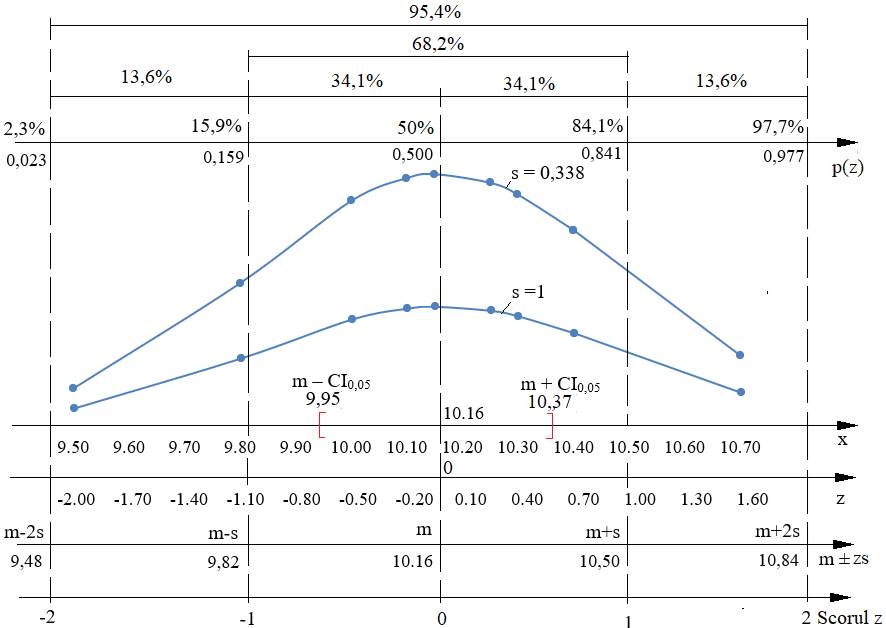
Fig. 2.29 Corespondența valorilor densității de probabilitate în coordonate x, z și unități de abatere standard

a b c

Fig. 2.30 Intervale de încredere și probabilitățile corespunzătoare, asociate: a – unei unități standard; b – a două unități standard; c – a trei unități standard

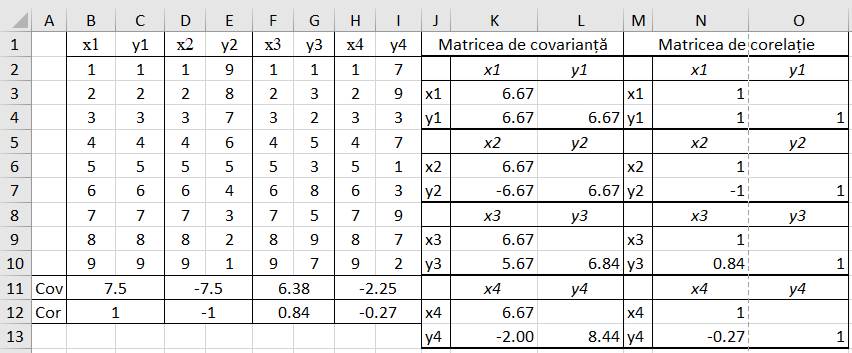
2.5.3.7 Indicatori statistici de corelare (asociere) a două variabile: Coeficientul de covarianță, Coeficentul de corelație, Matricea de covarianță

Ap.2.06 Determinarea indicatorilor statistici de corelare (asociere) pentru un set de măsurători (perechile (x₁, y₁), (x₂, y₂), (x₃, y₃) … (x₉, y₉)) cu n = 9 valori din coloanele B, C, D, E, F, G, H, I din fig. 2.31 (Ghid.Ap.2.06).

Semnificații

Coeficientul de covarianță exprimă prin valori numerice tipurile posibile de asocieri (corelări) liniare dintre două variabile și se calculează cu relațiile,

Cov = , pentru eșantioane

sau

COV = , pentru populații statistice,

unde, m_x și m_y (µ_x și µ_y) reprezintă mediile variabilelor x și respectiv y, asociate eșantioanelor (populații statistice), n – numărul de valori al variabilelor; funcții Excel: COVARIANCE.S, pentru eșantione (variabile cu n redus), COVARIANCE.P, pentru populații statistice (variabile cu n foarte mare).

Coeficențul de corelație, numit și r Perason, exprimă numeric tipurile și nivelurile împrăștierilor perechilor de valori (puncte) privind asocierile (corelările) a două variabile în scoruri standard [-1, 1] (Scorul z) și se calculează cu relația,

Cor = ,

în care, s_x și s_y reprezintă abaterile standard ale variabilelor; funcția Excel CORREL.

Matricea de covarianță are forma,

	x	y
x
y

unde, VAR(x) și VAR(y) reprezintă dispersia (varianța) variabilelor x și y; COV(x,y) = COV(y,x) – coeficientul de covarianță a variabilelor. Funția Excel: din modulul Data Analysis.

Matricea de corelație are forma,

	x	y
x
y

unde, valorile elementelor diagonalei principale sunt egale cu 1 (varianțele variabilelor x și y exprimate în unități standard (scorul z); Cor(x,y) = Cor(x,y) reprezintă coeficientul de corelație a variabilelor. Funția Excel: din modulul Data Analysis

Interpretări

Coeficientul de covarianță (Cov) evidențiază tipul corelației (asocierii) a două variabile (cu același număr de valori): valori pozitive (Cov > 0, fig. 2.30) arată dependență pozitivă (creșterea variabilei x induce creșterea variabilei y, linia este ascendentă, fig. 2.32,a,c); valori negative (Cov < 0, fig. 2.30) arată dependență negativă (creșterea variabilei x induce descreșterea variabilei y, linia este descendentă, fig. 2.32,b,d); valoarea zero evidențiază inexistența unei dependențe a celor două variabile.

Coeficientului de corelație evidențiază tipul corelației (asocierii) a două variabile (cu același număr de valori): valori pozitive subunitare (0 < Cor ≤ 1], fig. 2.30) arată dependență pozitivă (fig. 2.32,a,c); valori negative subunitare [-1 ≤ Cor < 0), fig. 2.30) arată dependență negativă (fig. 2.32,b,d); valoarea zero evidențiază inexistența unei dependențe a celor două variabile. În plus, valorile coeficientului de corelație indică și nivelul de împrăștiere (grupare) a perechilor de valori (puncte): = 1, arată nivel de împrăștiere ideal (toate punctele sunt grupate pe o linie, fig. 2.32,a,c); 0 < ≤ 1, nivel de împrăștiere (grupare) între limita înferioară (valoare apropiată de zero corespunzătoare nivelului de împrăștiate larg (fig. 2.32,d)) care induce asociere slabă și limita superioară (valoare apropiată de unu corespunzătoare nivelului de împrăștiate puternic (fig. 2.32,c) care induce asociere puternică. În literatura de specialitate se menționează pentru practică următoarele niveluri de împrăștiere (asociere): perfectă (ideală), = 1 (fig.2.32,a,b); puternică, 0,7 ≤ < 1 (fig.2.32,c); medie, 0,4 ≤ < 0,7 ; slabă, 0 < < 0,4 (fig.2.32,d).

Obs. Pentru determinarea indicatorilor de corelare, preliminar, se verifică: variabilele să fie perechi; lipsa valorilor extreme; seturile de date să fie fie distribuite cvasinormal.

Matricea de covarianță sintetizează sintetic valorile varianțelor și covarianțelor. În fig.2.31 se evidențiază că valorile obținute cu funcția din pachetul Data Analysis sunt calculate cu funcțiile Excel VAR.P și COVARIANCE.P, specifice populațiilor statistice care sunt diferite de cele obținute cu funcțiile Excel VAR.S și COVARIANCE.S pentru eșantioane (inclusiv, pentru cazurile din fig. 2.31; de ex. coeficinții de covarianță din matricele de covarianță (valorile din coloana K) sunt diferiți cei din linia 11, fig. 2.31.

Matricea de corelație sintetizează sintetic valorile varianțelor și covarianței corespunzătoare variabilelor exprimate în coordonate standad (Scorul z); valoarea coeficientului de corelație (fig. 2.31) este aceași cu cea obținută cu funcția Excel CORREL (v. coloana N și linia 12 din fig. 2.31

Fig. 2.31 Tabel cu valori ale datelor și indicatorilor de corelare

a	b
c	d
Fig. 2.32 Tipuri de corelații (asocieri): a – perfectă dependentă pozitiv; b – perfectă dependentă negativ; c – puternică dependentă pozitiv; d – slabă dependentă pozitiv

2.5.4 Analize statistice descriptive

În practică, nu se pot face un număr foarte mare de măsurători şi, deci, valoarea reală (adevărată) nu se poate determina direct. Generarea unei curbe de distribuție ce caracterizează populația statistică (cazul teoretic, general) din care face parte eșantionul (cu un număr de valori redus) este primul pas al statisticii descriptive bazată pe legi probabilistice. Pentru cazul teoretic (populația statistică cu un număr infinit de valori) indicatorii principali, media μ și dispersia (varianța) σ², se vor determina prin studii (analize) statistice descriptive bazate pe indicatorii principali, m și s², asociați valorilor obținute prin măsurare la nivel de eșantion.

Analizele statistice se ocupă cu descrierea, organizarea și sistematizarea trăsăturilor unui set de date obținut prin măsurare, de obicei, asociat unui eșantion, care se pot face prin analiza valorilor unor indicatori statistici (media, dispersia, mediana, cuantile, tendințe etc.) sintetizați tabelar cât şi/sau prin grafice (prin puncte, cu linii, histograme, boxplot etc.).

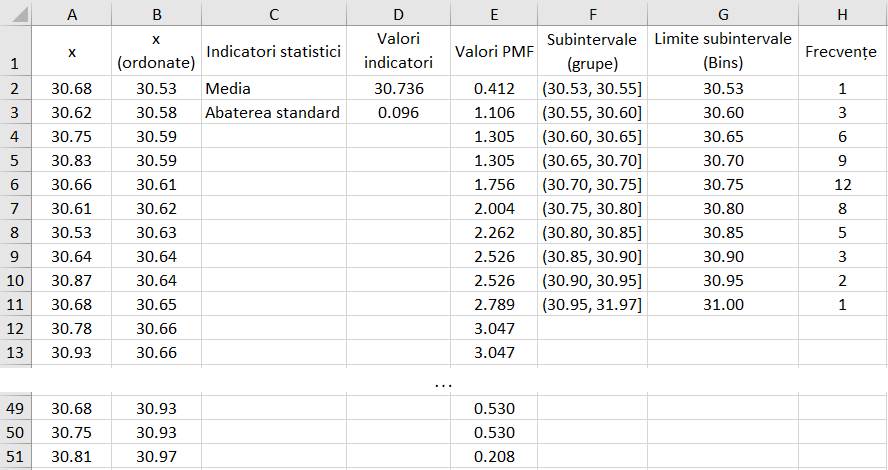
2.5.4.1 Analize statistice descriptive bazate pe reprezentări grafice ale frecvențelor

Ap.2.07 Determinarea pornind de la valorile un set de măsurători (coloana A din fig. 2.33) a grupelor (subintervalelor, claselor) de valori ale frecvențelor, poligonului frecvențelor, histogramei frecvențelor, graficului distribuției normale etc. (Ghid.Ap.2.07)

Semnificații

Frecvența absolută (simplă) (fa) reprezintă numărul care arată de câte ori se repetă o valoare numerică dintr-un set de date; suma frecvențelor simple reprezintă numărul de valori al setului de date, n. Frecvența relativă, (fr) proporția frecvenței simple a unei valori raportă la numărul total de valori fr = fa/n; uneori, se înmulțește cu 100 pentru a se obține procente (%). Deoarece, în urmă unor măsurători se obțin variabile continue sau numerice cu număr de valori mărit și cu amplitudinea (Max-Min) mare, pentru reducerea volumului de date, preliminar analizelor statistice se realizează gruparea valorilor în subintervale (grupe, clase); pentru cazul intervalelor egale, mărimea intervalului se determină prin împărțrea amplitudinii (Amp) la numărul de subintervale. Poligonul și/sau histograma frecvențelor valorilor (frecvent, incluse în grupe de valori) se pot considera ca distribuții ale valorilor frecvențelor care se pot folosi pentru compararea cu curbele de distribuție a unor legi de probabilitate teoretice (considerate ca referințe). Graficul distribuției normale (curba clopot, Gauss) efectivă vizualizează împrăștierea valorilor variabilei în jurul mediei, căreia îi corespunde vârful acestui grafic (v. fig. 2.8); funcția Excel NORM.DIS care are ca parametrii media (m) și abaterea standard (s)

Interpretări

În fig. 2.34 se observă că curba distribuției (poligonul) frecvențelor este asimetrică în raport cu valorea medie (m = 30,736) și are zonele marginale inegale. Aceasta evidențiază abateri semnificative față de curba ideală (clopotul lu Gauss, marcat cu roșu) și deci concluziile statistice vor fi cu erori. Aceași situație se evidențiază în fig. 2.35 unde alura histogramei (inclusiv a poligonului asociat, maract cu verde) este cu abateri față de distribuția normală (curba clopot, maractă cu roșu) a valorilor setului de date. Obs. În fig. 2.34 Bins reprezintă limitele subintervalelor (fig. 2.33). Curba clopot (distribuția normală, Gauss) efectivă pentru cazul numărului redus de valori (fig. 2.34, 2.35) are abateri față de cea teoretică (ideală) cu numere foarte mari de valori (fig. 2.36) care este netedă, simetrică în raport cu media, are cel mai mare număr de valori (peste 95%) în zona centrală și mult redus în zona ramurilor (cozilor) asimptotice din zonele marginale

Fig. 2.33 Tabel cu valori ale datelor, indicatorilor și frecvențelor

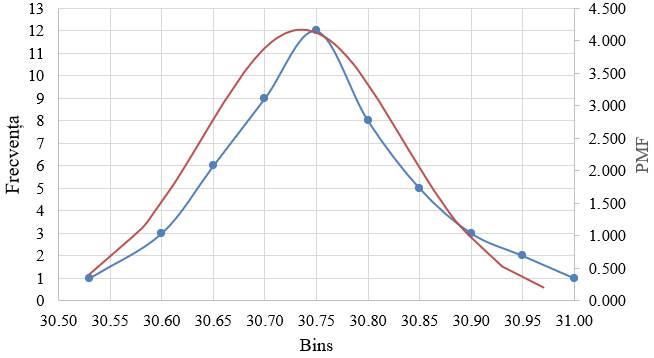
Fig. 2.34 Curba distribuției normală asociată curbei frecvențelor

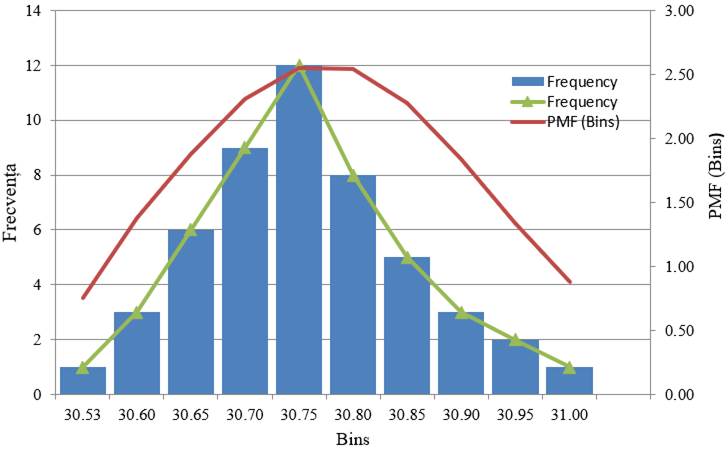
Fig. 2.35 Curba distribuției normală asociată histogramei și poligonului frecvențelor

Fig. 2.36 Curba teoretică ideală (Gauss) a distribuției normală (pentru un număr foarte mare de valori, n → ∞)

2.5.4.2 Analize statistice descriptive bazate pe reprezentări grafice de tip boxplot

Ap.2.08 Studiul, pornind de la valorile un set de măsurători (coloana A, din fig. 2.33), a unor aspecte privind: grafice boxplot și cazuri posibile; evidențierea valorilor aberante folosind regulile IQR și Standard Deviation (68-95-99,7) (Ghid.Ap.2.08)

Semnificații

Grafice boxplot (box-and-whiskers, cutie și mustăți) sunt folosite pentru vizualizarea răspândirii valorilor unei variabile grupate în patru subintervale (grupe): [Min, Q1], (Q1, Q2], (Q2, Q3] și (Q3, Max] care fiecare conțin câte 25% din valorile variabilei (fig. 2.37). Intervalul intercuartile (IQR) reprzintă domeniul limitat de caseta centrală a graficului cu mărimea Q3-Q1 și evidențiază 50% din valorile variabilei. Regula “1,5 IQR” permite identificarea valorilor aberante (outliers) mici sau mari care se găsesc în afara intervalului, [Q1 – 1,5*IQR, Q3 + 1,5*IQR] unde IQR = Q3 -Q1 reprezintă intervalul intercuartil, IQR

Interpretări

Identificarea formei graficului boxplot se face prin analiza șirului compus din 5 valori (numere) Max, Q1, Q2 (mdiana), Q3, Max (fig. 2.38,a, simetrică; 2.38,b, asimetrică negativ (stânga); 2.38,c, asimetrică pozitiv (dreapta)); cuartilele Q1 și Q2 sunt medianele valorilor localizate în stânga și, respectiv, dreapta medianei centrale; cozile simetrice indică distribuție simetrică (curbă clopot); coadă mai lungă spre stânga/dreapta arată că 50% din totalul dispuse între Min și Cuartila Q1 și între Cuartila Q3 și Max, sunt distribuite asimetric în jurul mediei. Graficele boxplot pot fi folosite și pentru compararea distribuțiilor, de ex. în fig.2.39 pentru cele două distribuții 1 și 2 se evidențiază următoarele: media distribuției 1 este mai mare decât a distribuției 2; dispersia distribuției 1 este mai mică decât a distribuției 2. Valorile aberante se identifică în afara intervalului valorilor acceptabile (regula „1,5IQR”), [Q1-1,5I*QR, Q3+1,5*IQR] (fig. 2.37). Aceste valori, de obicei, nu se încadrează în distribuții normale și se impune să fie eliminate în analizele statistice ulterioare sau în cazurile când acestea sunt multe numeric este indicat să se repete măsurătorile. Determinarea valorilor aberante este o operație aproximativă care se poate face și în raport cu valorile abaterilor standard (regula “68-95-99,7”) care aproximează procentual repartizarea valorilor unui set de date în domenii limitate de valori ale abaterii standard fig.2.40). Graficele boxplot au avantajul reprezentării sintetice în spații mult reduse și pot fi folosite în favoarea reprezentărilor sub formă de poligoan, histogramă și distrubuție

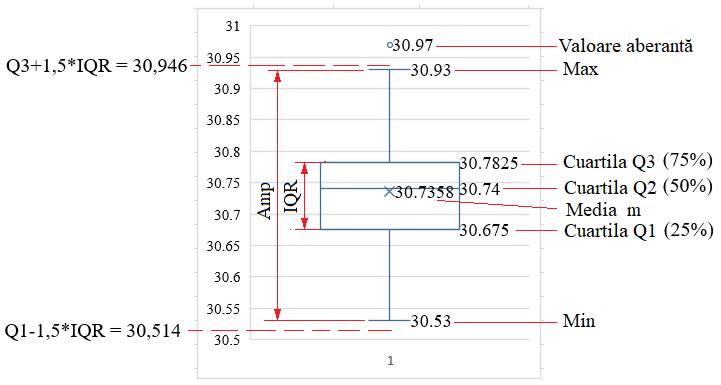
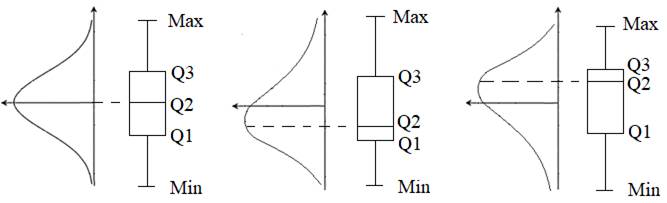
Fig. 2.37 Structura generală a graficului boxplot asociată datelor din fig. 2.33

a b c

Fig. 2.38 Forme ale graficelor boxplot asociate cu forme ale disttribuției normale în jurul mediei: a – simetrică; b – asimetrică negativ; c – asimetrică pozitiv

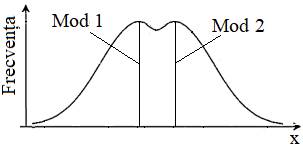
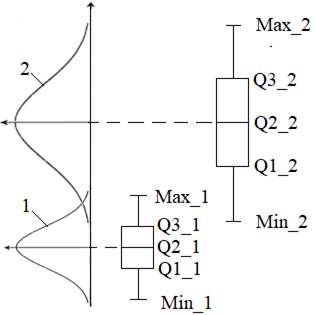
Fig.2.39 Grafice boxplot asociate cu două distribuții normale

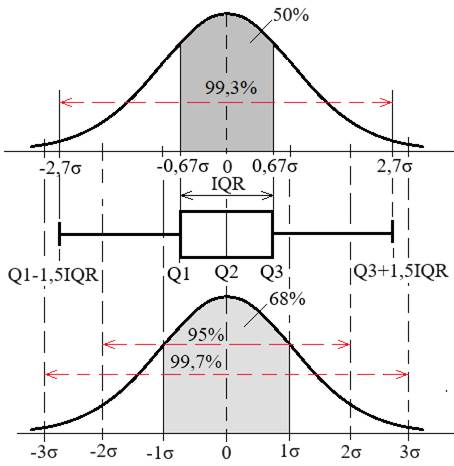
Fig.2.40 Graficul boxplot corelat cu distribuția normală dependentă de valori ale abaterilor standard

2.5.4.3 Analize statistice descriptive bazate pe reprezentări grafice a distribuției (repartiției) datelor

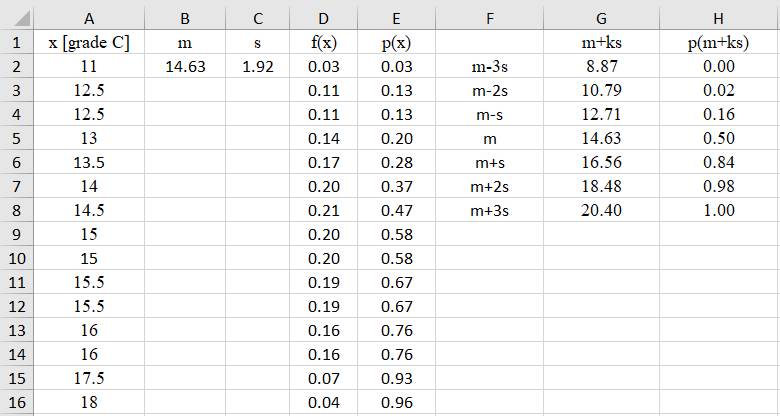
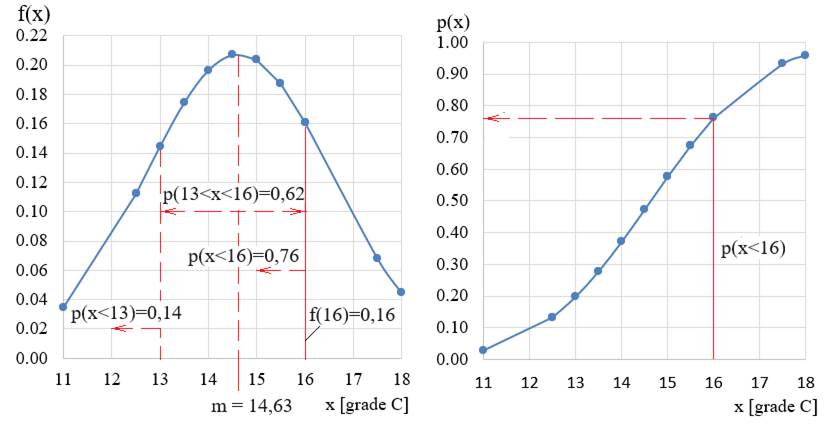
Ap.2.09 Studiul statistic bazat pe funcțiile de distribuție (repartiție) și probabilitate a unui set de date asociat temperaturilor unui corp (coloanal A, fig. 2.41) în vederea stabilirii temperaturii medii (Ghid.Ap.09).

Semnificații

Pentru acest studiu statistic se vor folosi funcțiile de distribuție (repartiție) normală efectivă, f(x), și densitate de probabilitate cumulată, p(x). Funcția de distribuție (repartiție) normală efectivă, f(x), asociată setului de date considerat (coloana A, din fig. 2.41) se determină cu funcţia Excel NORM.DIST, pentru variabila (fig. 2.42); se va adopta varianta FALSE, corespunzătoare opțiunii PMF (Probability Mass Function). Funcția densitate de probabilitae (cumulată), p(x), asociată setului de date considerat (coloana A, din fig. 2.41) se determină cu funcţia Excel, NORM.DIST, pentru variabila x (fig. 2.41); se va adopta varianta TRUE, corespunzătoare opțiunii CDF (Cumulative Density Function). Pentru determinarea acestor funcții se impune calculul valorilor indicatorilor: media (aritmetică), funcția Excel AVERAGE, și Abaterea standard (STD) cu funcția Excel, STDEV.S (pentru eșantioane, cu numere de valori reduse)

Interpretări

Valoarea funcției de repartiție corespunzătoare unei valori curente a setului de date reprezintă ponderea (contribuția) acesteia în valoarea mediei, m. Valoarile funcţiei densitate de probabilitate cumulată (aria de sub graficul de repartiție) reprezintă ponderea (probabilitatea) valorilor mai mici decât o valoare curentă a variabilei statistice x în valoarea mediei, m. Pentru evidențierea aproprierii (suprapunerii) distribuției, asociată valorilor unui eșantion, de distribuția normală de referință (Gauss), se vor compara valori efective ale funcției de repartiție, asociată eșantionului, cu valori ale distribuției normală de referință. Caracterizarea funcțiilor de repartiție și de probabilitate prin comparație cu distribuția normală de referință (teoretică) presupune urmărirea încadrării în (aproprierii de) următoarele caracteristici (v. fig. 2.12): - valorile sunt repartizate într-un domeniu de aproximativ 6σ (șase abateri standard), trei la stânga și trei la dreapta mediei (de obicei, valorile în afara acestor limite, dacă există, sunt nesemnificative (aberante); - aproximativ jumătate din valori se găsesc în dreapta mediei și cealaltă în stânga acesteia; - 68% din valori se află în intervalul [µ-σ, µ +σ]; 95% din valori se află în intervalul [µ-2σ, µ+2σ]; 99,7% din valori se află în intervalul [µ-3σ, µ+3σ]; Obs. În plus, distribuția normală de referință (teoretică) are și următoarele caracteristici: media și mediana sunt identice (fig. 2.19,a); este simetrică (Skew = 0, v. fig. 2.21) și mezocurtică (Kurt = 0, v. fig. 2.22). Pentrul setul de date considerat (coloana A, fig, 2.41) se evidențiază următoarele (fig, 2.42): - ponderea temperturii x = 13^oC în valoarea medie (m = 14,63^oC) este f(13) = 0,2 (20%); - ponderea temperturii x = 16^oC în valoarea medie (m = 14,63^oC) este f(16) = 0,16 (16%); - probabilitatea cumulată a temperaturilor mai mici de 13^oC (x < 13), în valoarea medie (m = 14,63^oC) este p(x<13) = 0,14 (14%); - probabilitatea cumulată a temperaturilor mai mici de 16^oC (x < 16), în valoarea medie (m = 14,63^oC) este p(x<16) = 0,76 (76%); - probabilitatea cumulată a temperaturilor mai mici de 16^oC (x < 16) și mai mari ca 13^oC, în valoarea medie (m = 14,63^oC) este p(13<x<16) = 0,76 – 0,14 = 0,62 (62%); În cazul reprezentării variabilei în valori m+ks (k ϵ { ± 3, ±2, ±1, 0} (scorul z) și calculul funcției de probabilitate cumulată asociată (coloanele G și H din fig. 2,41; fig. 2.43) se evidențiază următoarele: - 68% din valorile temperaturilor se află în intervalul [m-s, m+s] = [12,71; 16,56] ^oC; - 96% din valorile temperaturilor se află în intervalul [m-2s, m+2s] = [10,79; 18,48] ^oC; - 100% din valorile temperaturilor se află în intervalul [m-3s, m+3s] = [8,87; 2,40] ^oC. Concluzie. Din analiza comparativă a valorilor rezultate pentru funcțiile asociate distribuției normală efectivă, simetrică în raport cu media și cu probabilitățile de grupare 68%, 96%, 100%cu cele asociate distribuției normală de referință (68%, 96%, 99,7%) se evidențiază o “apropriere“ semnificativă și deci valoarea medie obținută se poate considera semnificativă.

Fig.2.41 Tabel cu valori ale datelor, indicatorilor și probabilităților

Fig.2.42 Valori ale probabilităților cumulate corespunzătoare unor valori distincte sau intervale

Fig.2.43 Valori ale intervalelor de încredere și probabilitățile impuse corespunzătoare

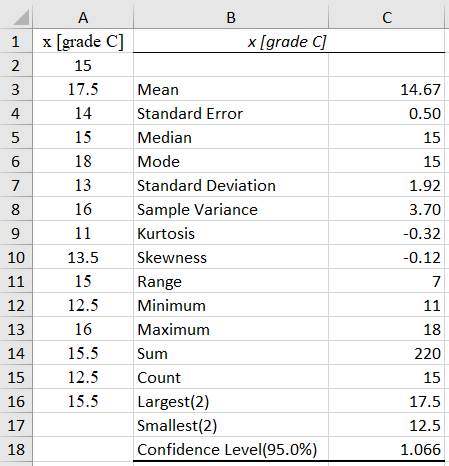
2.5.4.4 Analize statistice descriptive bazate pe valori ale indicatorilor statistici

Ap.2.10 Studiul statistic, bazat pe valori ale indicatorilor obținuți cu funcția Descripive statistics din modulul Data Analysis, a unui set de date asociat temperaturilor unui corp (coloana A, fig.2.44) în vederea stabilirii temperaturii medii (Ghid.Ap.2.10).

Semnificații

Funcția Descripive statistics din modulul Data Analysis implică determinarea pentru un set de date (coloanal A din fig. a) a indicatorilor statistici: Mean, media aritmetică; Standard Error, Eroarea standard; Median, Mediana; Mode, mod; Standard Deviation, Abaterea standard; Sample Variance, varianța; Kurtosis, boltirea; Skewness, asimetria; Range, amplitudinea; Maximum, maximul; Minimum, minimul; Sum, suma; Count, numărul valorilor. Largest(k), valoarea cea mai mare cu poziția k; Smallest(k), valoarea cea mai mică cu poziția k (k = 1…Count-1).

Interpretări

Valorile indicatorilor statistici determinați cu funcța Descripive statistics permit evaluarea aspectelor legate de: de tendința centrală: (Mean, Mediana, Mod, Sum, CountI); împrăștierea (dispersia) valorilor (Simple Variance, Standard Deviation, Min, Max, Range, Largest(k), Smallest(k)), forma curbei de distribuție (Kurtosis, Skewness). Caracterizarea unei distribuții normale de referință (teoretică) asociată unei populații (teoretic cu număr foarte mare de valori, N → ∞): - să fie unimodală, o singură valoare cu frecvența maximă; - media µ și mediana sunt identice; - curba de reparție (distribuție) este simetrică (Skew = 0) și normal boltită, mezocurtică (Kurt = 3); adică să nu fie nici prea ascuțită (foarte omogenă) și nici prea turtită (foarte eterogenă; - valorile sunt repartizate într-un domeniu de aproximativ 6σ (șase abateri standard), trei la stânga și trei la dreapta mediei (de obicei, valorile în afara acestor limite, dacă există, sunt nesemnificative (aberante); - aproximativ jumătate din valori se găsesc în dreapta mediei și cealaltă în stânga acesteia; - 68% din valori se află în intervalul [µ-σ, µ +σ]; 95% din valori se află în intervalul [µ-2σ, µ+2σ]; 99,7% din valori se află în intervalul [µ-3σ, µ+3σ]; - eroarea standard, ES = 0; media este ideal reprezentativă. Pentru aprecierea distribuției valorilor unui eșantion se pot considera următoarele categorisiri: - coieficientul de asimetrie: -0,5 ≤ Skew ≤ 0,5, curba de distribuție este ușor simetrică; -1 ≤ Skew ≤ -0,5 sau 0,5 ≤ Skew ≤ 1 – moderat simetrică; Skew ≤ -1 sau 1 ≤ Skew – puternic asimetrică. - coeficientul de boltire: Kurt < 3, formă aplatizată (platicurtică); Kurt = 3, formă oloan; Kurt > 3, formă ascuțită (leptocurtică). Pentru aprecierea estimării valorii medii a unui eșantion se pot considera următoarele: - valoarea mediei m, corespunzătoare unui eșantion cu n valori aparține intervalului de încredere , [m – Ea max, m + Ea max] cu Ea max = s unde k = 1, 2, 3 pentru valori ale pragului (nivelului) de încredere (Confidence level) 90%, 95%, respectiv 99%; - Eroarea Standard (ES) se determină cu relația, ES = s/, și reprezentă o estimare a abaterii mediei unui eșantion (numărul de valori n redus) față de media populației statistice (n → ∞), pentru care ES → 0 - coieficientul de variație (CV), definit ca raport dintre abaterea standard şi medie (numai pentru cazurile cu media diferită de 0), CV = s/m, de obicei, este exprimat în procente, indică nivelul de grupare a valorilor în jurul mediei (valori mai mici evidențiază o grupare mai bună). Obs. Intervalul de încredere reprezintă domeniul în care se bănuieşte că există valoarea reală (adevărată) a parametrului măsurat cu o probabilitatea impusă, numită prag (nivel) de încredere (siguranță), p, corespunzător unui nivel (prag) de semnificație (risc), α = 1 – p. De regulă, p > 0,9 și deci α < 0,1; astfel, dacă α = 0,05 (5%) atunci, p ≥ 1 – α = 0,95 (95%) şi deci, eroarea de estimare va fi sub 5%. Pentru estimarea mediei unei populații se pleacă de la valoarea mediei m calculată la nivel de eșantion și se determină un interval de încredere în care se găsește media populației µ. Din analiza valorilor indicatorilor statistici obținuți pentru setul de valori (coloana A, fig.2.44) rezultă următoarele: - media, m = 14,67^oC, modul, Mod = 15^oC, și mediana, Med = 15^oC, sunt cvasiidentice și arată simetria distribuției valorilor față de medie; - coeficientul de asimetrie, Skew = -0,12, indică asimetrie ușoară spre stânga; - coieficientul de boltire, Kurtosis = -0.32, indică distribuție moderat platikurtică; - amplitudinea (range), Amp = 7, este mai mică decât (6*abaterea standard), 6*s = 6* 1,92 = 11,52, indică că toate valorile sunt în domeniul de normalitate; - domeniul [Smallest(2), Largest(2)] = [12,5, 17,5] indică “aproprierea“ valorilor extreme de valorile centrale; este posibil pentru calculul mediei să se elimine valorile extreme (Max, Min) și să se obțină o valoare acesteaia mai semnificativă; - valoarea mediei m = 14,67^oC aparține intervalului de încredere, [m – Ea max, m + Ea max] cu Ea max = s = 1,92 = 0,99 ^oC; deci, valorile m ϵ [13,68, 15,66] ^oC cu o probabilitate de 95,5%; - valoarea coeficientului de variație, CV = s/m = 1,92/14,67 = 0,13 (13%) indică o grupare bună a valorilor variabilei în jurul mediei. Concluzie. Având în vedere valorile indicatorilor mai sus analizați se poate considera că valoarea mediei m este moderat reprezentativă

Fig. 2.44 Tabel cu valori ale datelor și indicatorilor

(CONTINUARE la subcap. 2.5.5)