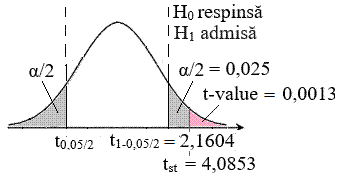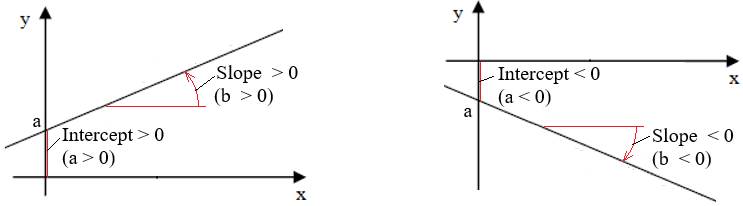Mogan Gh.L., Butnariu S.L., Buzdugan I.D. Organe de mașini. Lucrări de laborator. Universitatea Transilvania din Brașov

1. PRELUCRAREA ŞI ANALIZA STATISTICĂ A DATELOR EXPERIMENTALE

(REVENIRE la Cuprins )

2.5.5 Analize statistice inferenţiale (deductive)

2.5.5.1 Aspecte generale

În multe probleme de inginerie se pune problema acceptării sau respingerii valorilor obținute prin măsurători. Atunci cînd o investigaţie de tip statistic se efectuează bazat pe date asociate unui eşantion, orice rezultat obţinut are o valoare relativă, în sensul că datele respective nu numai că nu coincid cu cele referitoare la cazul general (populaţia statistică), dar nici măcar nu se poate afirma cu certitudine care este diferenţa dintre cele două seturi de date, asociate eșantionului și populației, care, de regulă, sunt necunoscute.

Statistica inferenţială (inductivă, deductivă) permite obţinerea de concluzii cvasiprecise (uneori, precise) despre anumite trăsături (caracteristici) ale unei mulţimi (populație, caz general, caz teoretic), de obicei, cu un număr foarte mare de valori (teoretic infinit). Analizele inferențiale de obicei au la bază o submulţime (uneori, două sau mai multe) asociată unui eșantion cu un număr finit, de regulă mult redus, de valori (frecvent, n < 30). Spre deosebire de staistica descriptivă, care trage concluzii bazat pe date (indicatori) cu valori ferme, prin statistica inferențială se ajunge la date (concluzii) noi bazat pe legi probabilistice aplicate la nivel de eșantion (eșantioane).

Concluziile (deciziile, estimările, extrapolările) ca rezultat al studiilor inferențiale sunt validate, de obicei sub rezerva unor certititudini/incertitudini (probabilități impuse/riscuri acceptate) pentru o mulţime infinită (cazul general, populație statistică), bazat pe indicatori statistici descriptivi asociați datelor unuia sau mai multor submulțimi (eșantioane) cu numere de valori, obținute prin măsurare, reduse.

Scopul inferenţelor (testelor) statistice este să determine dacă există suficiente dovezi statistice care să permită să se concluzioneze că o afirmaţie (ipoteză) despre un parametru este adevărată. Testele statistice verifică dacă una sau mai multe ipoteze formulate cu privire la o populație au șanse să fie adevărate; de ex. dacă pentru valorile unui experiment se observă concordanțe/diferențe de comportare a valorilor la nivel de eșantion, oare și la nivel de populație (caz general) apar concordanțe/diferențe; în urma testului statistic se poate răspunde: da/nu, acceptat/respins.

Metodele și tehnicile statisticii inferențiale, spre deosebire ale statisticii descriptive (de obicei, comparative), pot fi: de predicție (estimare) a unor caracteristici comune ale populației și de decizie, care implică verificarea unor ipoteze statistice la nivel de populații formulate pe baza rezultatelor obținute la nivel de eșantion. Astfel, testele statistice răspunde la întrebări (ipoteze) care se referă la comportarea (evoluția) fenomenelelor sau proceselor studiate.

Statistica deductivă are ca scop obținerea de decizii (concluzii) despre datele de analizat care pot lua diverse forme: răspunsuri da/nu la întrebări despre ipoteze asociate datelor (teste de decizie), estimarea caracteristicilor numerice ale datelor (teste de estimare), descrierea asocierii și/sau corelațiilor de date (teste de corelare).

2.5.5.2 Modelarea problemelor de statistică inferențială

În studiile experimentale (inclusiv, cele inginerești) verificarea ipotezelor ştiinţifice se face cu teste specifice bazate pe ipoteze statistice, formulate la nivel de populație (cazul general, N → ∞) pentru a arăta care sunt certitudinile ca acestea să fie adevărate. Astfel, se testează ipoteze asociate cazului general, formulate pe baza datelor obținute pentru unul sau mai multe eșantioane (cu, numărul de măsurători, n, mic).

Ipoteza statistică (parametrică) este o afirmație (presupunere) cu privire la parametri (indicatori) statistici (de obicei, media și/sau dispersia) asociați unei variabile corespunzătoare unei populații care se verifică, având la bază un set de date de măsurare (asociate unui eșantion), cu ajutorul unui test statistic; în urma rezolvării acestuia ipoteza statistică se poate accepta sau respinge cu o probabilitate (risc) impusă.

Testele statistice sunt metode prin care se iau decizii, care permit, ca pentru unul sau mai multe seturi de date experimentale, valori numerice, să se valideze anumite estimări de parametri asociați unei repartiţii probabilistice sau chiar, uneori, să se poată prezice forma legii de repartiţie a datelor. Prin aceste metode se verifică o ipoteză de nul (de obicei, cea pe care cercetătorul urmărește să fie invalidată) care dacă va fi respinsă se va accepta, ipoteza alternativă și, deci, se confirmă ipoteza de cercetare.

Ipoteza de nul presupune (intuieşte) apriori ca fiind adevărată situaţia cea mai apropiată de realitate, desigur cu admiterea caracterului întâmplător al abaterilor. Aceasta se specifică cu simbolul “=” (egalitate statistică, care ca valoare numerică poate fi diferită), adică, nu există nicio diferență, cu o probabilitae impusă, între parametrii studiați (medie, disperse). Ipoteza alternativă reprezintă o situație admisibilă contrară (opusă) cu ipoteza nulă (există diferență între parametri studiați, de obicei, conform ipotezei de cercetare). Aceasta se specifică cu simbolurile: “>”, “<” sau “≠”.

Prin respingerea ipotezei de nul (la un nivel de semnificație (risc) statistică) se indică că rezultatele observate (diferențele) nu sunt datorită întâmplărilor și SUNT semnificative statistic. Când ipoteza de nul este acceptată se indică că diferenţele observate sunt din cauza întâmplărilor şi rezultatele NU SUNT semnificative statistic.

La testarea ipotezelor statistice sunt posibile deciziile din tab.2.2; ipoteza nulă se respinge sau se acceptă (sau nu sunt motive de respingere a ei). Deci, testele statistice sunt metode (tehnici) de decizie care stau la baza validării sau invalidării cu un anumit grad de certitudine (risc) a unei ipoteze statistice. Semnificația statistică a unui test este indicată de probabilitatea de a obține o eroare de tip I. În cazul deciziilor false se pune problema minimizării erorilor posibile (de tip I și de tip II), de obicei, se minimizează eroarea cea mai dezavantajoasă (dependent de aplicație).

Tab. 2.2 Tipuri de decizii dependente de starea ipotezei de nul

Starea ipotezei, H0	Decizia (concluzia), legată de H0	Tipul deciziei	Eroare
Adevărată	Acceptată	Corectă
Adevărată	Respinsă	Falsă	De tip I
Falsă	Acceptată	Falsă	De tip II
Falsă	Respinsă	Corectă

Nivelul de semnificație (risc), de obicei, notat α, indică, pe de-o parte, probabilitatea maximă cu care se respinge ipoteza de nul (când, de fapt aceasta este adevărată) sau pe de altă parte, mărimea riscului (erorii) pe care cercetătorul este dispus să îl accepte; valori uzuale: α = 0,01 (1%), nivel puternic semnificativ, α = 0,05 (5%), nivel normal semnificativ sau α = 0,1 (10%), nivel slab semnificativ. Nivelul de încredere, de obicei notat, p = 1- α, reprezintă proabilitatea ca valorile rezultate să fie garantate (certe); corespunzător valorilor uzuale ale lui α: p = 0,99 (99%), p = 0,95 (95%), respectiv, p = 0,90 (90%).

2.5.5.3 Alegerea tipului testului statistic

Alegerea testului adecvat se face, pe de o parte, în funcţie de datele obținute prin măsurare (tipurile variabilelor), iar pe de altă parte, în funcţie de scopul urmărit. În cazul variabilelor numerice (rezultatele unor măsurători), se pot alege între două grupe de teste: parametrice şi nonparametrice. Testele parametrice au la bază presupunerea că datele provin dintr-o populaţie cu distribuţie normală (Gauss), iar testele cel mai des folosite sunt: testul z, testul t (Student), testul Fisher, de analiza a varianţei ANOVA (ANalysis Of VAriance).

Testele nonparametrice nu implică cunoașterea distribuției valorilor se bazează pe analiza ordinei valorilor, de obicei, neluând în considerare valori exacte operând cu valori arbitrare, cu grade de ambiguitate necontrolate; aceste teste, de obicei, fiind neadecvate pentru studiile experimentale inginerești nu se vor trata în continuare.

Teste statistice parametrice pentru verificarea ipotezelor statistice asupra parametrilor repartiției normale (media și/sau dispersia), frecvent, se folosesc pentru eșantioane cu:

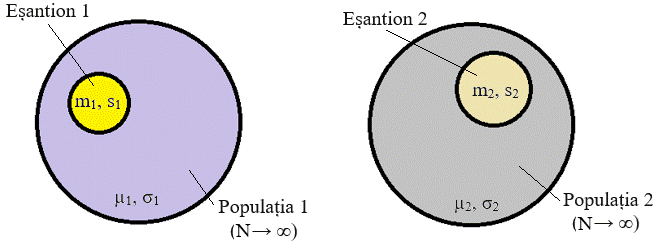
- n ≥ 30…100, cu repartiția normală; în practică se pot întâlni următoarele variante:

- testul z pentru medie (o variabilă), când NU se cunoaște dispersia populației σ²;

- testul t pentru medie (o variabilă), când se cunoaște dispersia populației σ² (este robust și mai stabil, deoarece are la bază dispersia populației);

- testul z pentru medii (două variabile, fig. 2.46), când NU se cunosc dispersiile populației , ;

- testul t pentru medii (două variabile, fig. 2.46), când NU se cunosc dispersiile populației și sunt diferite ≠ ;

- testul t pentru medii (două variabile, fig. 2.46), când NU se cunosc dispersiile populației dar se consideră egale ( = );

- testul F pentru dispersii (două variabile, fig. 2.46).

- n < 30 (eșantioane mici), chiar dacă variabila este normală, NU se folosesc testele z (deoarece rezultatele sunt alterate din cauza volumului de selecție, n, mic), se folosesc teste t indiferent dacă se cunoaște sau nu dispersia variabilei.

Fig. 2.46 Parametri principali a două populații și eșantioane asociate

Obs.

- spre deosebire de testul z care folosește și parametri de populație, fiind mai robust, testul t, bazat pe parametri de eșantion, este mai slab;

- pentru cazurile cu mai mult de două variabile se poate folosi testul ANOVA.

- în general, datele statistice legate de medie sunt înfluențate de dispersie și deci, fiind dependente de abaterea standard (σ), pun în evidență pe lângă tendința centrală (media) și variabilitatea.

2.5.5.4 Descrierea (formularea) problemei statistice

Pentru aplicarea unei analize (test) statistice deductivă de decizie, preliminar, se stabilesc următoarele:

- definirea populației statistice cu parametri µ, σ (de obicei, cu valori necunoscute);

- nivelul de semnificație (risc), α; nivelul de încredere, p = 1- α;

- volumul eșantionului (eșantioanelor): n valori;

- caractersistica (proprietatea) de interes, variabila aleatoare asociată, {x₁, x₂, …. x_n}, cu indicatorii statistici principali (m, s) cunoscuți;

- θ₀, parametrul de interes, impus (de obicei, o valoare de medie sau de dispersie);

- funcția statistică (normală (standard), Student t, Fischet F etc.) cu repartițe cunoscută;

- alegerea tipului testului statistic potrivit parametrului de interes și datelor aplicației.

2.5.5.5 Algoritm general de rezolvare a testelor statistice de semnificație

a. Formularea ipotezelor

Ipotezele statistice se stabilesc conform tab. 2.3.

Tab. 2.3 Formularea ipotezelor testelor de decizie

Ipoteza de nul, H0	Ipoteza alternativă, H1	Denumire test
θ1 = θ0 , θ1-θ0 = 0, pentru un parametru sau θ1, θ2; θ1-θ2 = 0, pentru doi parametri	θ1 < θ0	Unilateral stânga (left one-tail, coadă stânga), fig. 2.47,a
	θ1 > θ0	Unilateral dreapta (right one-tail, coadă dreapta), fig. 2.47,b
	θ1 ≠ θ2	Bilateral (two tail, două cozi), fig. 2.47,c
θ0, reprezintă valoarea impusă (de testare), de obicei, asociată mediei sau dispersiei

Obs. Ipoteza alternativă decide denumirea testului (unilateral stânga/dreapta sau bilateral). În practică sunt preferate ipotezele asociate cu testele unilaterale, deoarece conduc la rezultate mai relevante.

b. Adoptarea funcției statistice (FS), determinarea valorii acesteia și a semnificației statistice

Funcția statistică poate fi: normală (standard), Student t, Fischet F etc.; valoarea statistică u_st rezultă din ecuația FS(u) = θ₀; semnificația statistică efectivă, u-value = FS(z_st); valorile și semnificațiile statistice se pot determina cu funcții Excel.

c. Determinarea valorii critice

Se determină c_α, c_1-α sau c_α/2, c_1-α/2 din ecuația FS(c) = α; valorile se pot obține și cu funcții Excel; valoarea critică reprezintă cuantila de ordinul α egală cu aria de sub curba de reparție (probabilitatea) pentru valoarea x < c. Valoarea nivelului (pragului) de semnificație, α (0,01, 0,05 (frecvent folosit) sau 0,1), se stabilește în funcție de tipul aplicației.

Obs. valoarea critică împarte mulțimea valorilor statistice în două regiuni (fig. 2.47): critică (de respingere a ipotezei H₀, respectiv de acceptare a ipotezei alternative H₁), necritică (de acceptare a ipotezei H₀).

d. Concluzia (decizia) privind acceptarea/respingerea ipotezei de nul

Prin compararea valorii statistice u_st cu valori critice c_α sau a valorii pragului de semnificație u-value cu α, se pot obține variantele:

Cazul testului unilateral stânga (left one-tail, fig. 2.47,a)

u_st > c_α (u-value > α), ipoteza de nul H₀ este acceptată și este nesemnificativă statistic (probabilitatea p = α);

u_st < c_α (u-value < α), ipoteza de nul H₀ este respinsă și este semnificativă statistic; se acceptă H₁, ipoteza cercetării se confirmă) cu probabilitatea p = 1-α.

Cazul testului unilateral dreapta (right one-tail, fig. 2.47,b)

u_st < c_α (u-value > α), ipoteza de nul H₀ este acceptată și este nesemnificativă statistic (probabilitatea p = α);

u_st > c_α (u-value < α), ipoteza de nul H₀ este respinsă și este semnificativă statistic; se acceptă H₁, ipoteza cercetării se confirmă cu probabilitatea p = 1-α.

Cazul testului bilateral (two-tail (două cozi), fig.2.47,c)

u_st > c_α/2 sau u_st < c_1-α/2 (u-value > α/2), ipoteza de nul H₀ este acceptată și este nesemnificativă statistic (probabilitatea p = α);

u_st < c_α/2 sau u > c_1-α/2 (u-value < α/2), ipoteza de nul H₀ este respinsă și este semnificativă statistic; se acceptă H₁, ipoteza cercetării se confirmă cu probabilitatea p = 1-α.

a b c

Fig. 2.47 Cazuri posibile ale testelor de decizie: a - unilateral stânga (left one-tail, coadă stânga); b -unilateral dreapta (right one-tail, coadă dreapta); c - bilateral (two tail, două cozi)

2.5.5.6 Analize (teste) statistice de decizie/estimare

2.5.5.6.1 Aplicație testul z de medie pentru o variabilă

Ap.2.11 Să se verifice condiția de rezistența (să NU cedeze) la rupere a materialului unui lot de peste 10000 de piese, R < R₀ = 570 MPa cu probabilitatea 95% (ipoteza de cercetare), pornind de la un set de măsurători cu n =32 valori, ale tensiunilor efective (coloana A, fig. 2.48). Se consideră că distribuția valorilor variabilei, tensiunile efective, este normală (Ghid.Ap.2.11).

Descrierea problemei statistice:

- definirea populației: valorile rezistențelor (tensiunilor) efective ale pieselor lotului; se cunosc parametrii µ, σ considerați ca fiind egali cu ai eșantionului (acesta având volum mare, n ≥ 30;

- nivelul de semnificație: α = 0,05 (5%); nivelul de încredere (certitudine), p = 1- α = 0,95 (95%);

- volumul eșantionului: n = 32, valori (coloana A, fig. 2.47);

- caractersistica (proprietatea) de interes, variabila aleatoare: valorile (rezistențelor) tensiunilor efective, R, au distribuție normală (m, s);

- parametrul de interes; media m cu valoarea de referință R₀ = 570 MPa;

- funcția statistică: normală, f(x), cu dispersia s cunoscută;

- tipul testului: testul z, deoarece volumul eșantionului n ≥ 30 și repartiția valorilor este normală.

Rezolvarea testului

Semnificații

Personalizarea algoritmului general (v.subcap. 2.5.5.5)

a. Formularea ipotezelor

Ipoteza de nul, H0	Ipoteza alternativă, H1	Denumire test
R = R0	R < R0	Unilateral stânga (left one-tail), fig.2.49,a

Valoarea de referință a variabilei, R₀ = 570 MPa.

b. Adoptarea funcției statistice (FS) și determinarea valorii acesteia și a semnificației statistice asociată: normală standard, φ; din ecuația φ(z) = R₀, rezultă valoarea statistică; se determină cu funcția Excel. NORM.S.DIST sau cu funcția, din modul Excel Data

Analysis, se obține z_st = z = -3,1715 (fig. 2.48); semnificația statistică asociată, z-value, se determină cu funcția Excel, NORM.S.DIST(z_st,TRUE) sau cu = funcția, din modul Excel Data Analysis, se obține

z-value = = 0,0008;

c. Determinarea valorii critice: z_α, pentru α = 0,05 se determină pentru testul unilateral dreapta cu funcția Excel NORM.S.INV(α) sau cu opțiunea din Data Analysis z_0,05 = - = -1,6449 (fig.2.48).

d. Concluzia (decizia) privind acceptarea/respingerea ipotezei de nul (H₀): prin compararea valorii statistice z_st cu valori critice z_0,05 sau, pentru verificare, z-value cu α se pot obține: z_st < z_0,05 (-3,1715 < -1,6449), ipoteza de nul H₀ este respinsă (fig.2.48,a); această decizie este verificată și de inegalitatea: z-value < α (0,0008 < 0,05). În concluzie, se acceptă ipoteza alternativă H₁.

Interpretări

Pentru adoptarea ipotezei alternative H₁, R < R₀, s-a ținut cont de ipoteza de cercetare: verificarea rezistenței la rupere R < R₀, adică piesele să reziste (să nu apară cedarea prin rupere).

Valoarea statistică z_st s-a determinat în coordonate standard z.

Pentru luarea deciziei este suficient să se cunoască valorile funcției statistice z_st = -3,1715 și critică, z_0,05 = -1,6449 (fig.2.49,a); pe de altă parte, deciza se poate lua având la bază valoarea semnificației statistice asociată, z-value = 0,0008, și nivelul de semnificație, α = 0,05.

Respingerea ipotezei H₀, fig.2.48,a, conform testului z (personalizat mai sus)_, indică că media statistică a rezistențelor măsurate (eșantion), m =_s R₀ (550 egal statistic cu 570) cu nivelul de semnificație (risc), α = 0,05 (5%) și acceptarea ipotezei alternative H_1, indică că media statistică a rezistențelor măsurate (sintetizate în eșantion), m < R₀ (550 < 570 MPa) este semnificativă statistic cu nivelul de încredere (certitudine) p = 1-α = 0,95 (95%).

Dacă la formularea ipotezelor s-ar fi adoptat R₀ = 560 MPa prin aplicarea testului (Data Analysis) se obțin datele din fig. 2.49 (al doilea set de rezultate). În urma anlizei valorilor conform algoritmului de mai sus, se constată că z_st > z_0,05 (-1,6449 < -1,5857), respectiv, z-value > α (0,0564 > 0,05) și, deci, ipoteza de nul H₀ este acceptată fig.2.49,b cu nivelul de semnificație 0,05 (5%) și deci valoarea mediei, 550 < 560 MPa este nesemnificativă statistic cu probabilitatea de 95%.

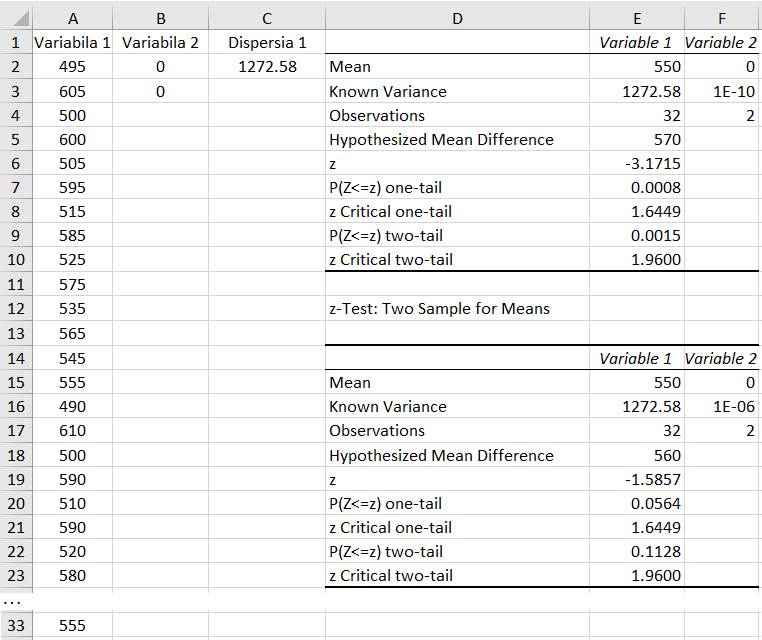
Fig. 2.48 Tabel cu valori ale datelor, indicatorilor și parametrilor statistici

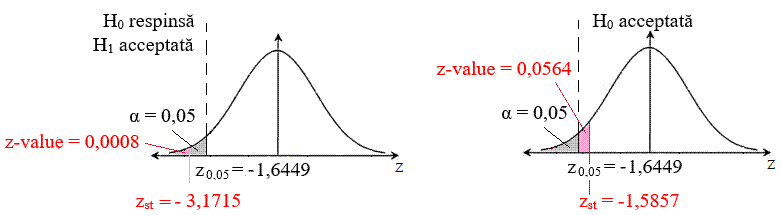
a b

Fig. 2.49 Scheme asociate testului: a – varianta ipotezei de nul respinsă; b – varianta ipotezei de nul acceptată

2.5.5.6.2 Aplicație testul t de medie pentru o variabilă

Ap.2.12 Să se determine rezistența la rupere R₀ la care cedează prin rupere piesele unui lot cu peste 10000 bucăți, cu certitudinea mai mare cu 95%, R > R₀ (ipoteza de cercetare), pornind de la un set de măsurători cu n =15 valori, ale tensiunii efective (coloana A, fig. 2.50,a). Se consideră că distribuția valorilor variabilei tensiunii efective nu este normală (Ghid.Ap.2.12).

Descrierea problemei statistice:

- definirea populației: valorile posibile ale rezistenței la rupere ale pieselor lotului; nu se cunosc parametrii µ, σ;

- nivelul de semnificație: α = 0,05 (1%); nivelul de încredere, p = 1-α = 0,95 (95%);

- volumul eșantionului: n = 15 valori (coloana A, fig. 2.50,a);

- caractersistica (proprietatea) de interes, variabila aleatoare: rezistența (tensiunea) la rupere, R;

- parametrul de interes; media m cu valoarea de referință R₀ (pentru început, se adoptă pentru R₀ o valoare din prima parte a domeniului a valorilor eșantionului, de ex. R₀ = 520 MPa; pentru valoarea R₀ egală cu minimul valorilor (de ex. 505 MPa) procentul de rezistență la rupere este maxim (spre 100%).

- funcția statistică: STUDENT;

- tipul testului: t (STUDENT), deoarece volumul eșantionului n < 30.

Rezolvarea testului

Semnificații

Personalizarea algoritmului general (v.subcap. 2.5.5.5)

a. Formularea ipotezelor

Ipoteza de nul, H0	Ipoteza alternativă, H1	Denumire test
R = R0	R > R0	Unilateral dreapta (left one-tail), fig.2.51

Valoarea de referință a variabilei, R₀ = 520 MPa.

b. Adoptarea funcției statistice (FS) și determinarea valorii acesteia și a semnificației statistice asociată: STUDENT(t); din ecuația STUDENT(t) = R₀, rezultă valoarea statistică; se determină cu funcția implementată în modul Excel Data Analysis și se obține t_st = = 2,5039 (fig.2.50,a); semnificația statistică asociată, t-value, se determină cu funcția, din modul Excel Data Analysis și se obține

t-value = = 0,0127 (fig.2.50,a);

c. Determinarea valorii critice: t_1-α pentru α = 0,05; se determină cu opțiunea din Data Analysis, t_1-0,05 = = 1,7613 (fig.2.50,a; 2.51);

d. Concluzia (decizia) privind acceptarea/respingerea ipotezei de nul (H₀): prin compararea valorii statistice t_st cu valoarea critică t_1-α se obțin: t_st > t_1-0,05 (2,5039 > 1,7613) sau t-value < α (0,0127 < 0,05), ipoteza de nul H₀ este respinsă fiind semnificativă statistic cu probabilitatea t-value = 0,0127 (1,27%).

Maximizarea preciziei rezultatului testului

Deoarece probabilitatea de respingere a ipotezei H₀ este mult prea mică (1,27%) decât nivelul de semnificație (5%) și deci eroarea (abaterea) de apreciere prea mare, se continuă testul în vederea micșorării diferenței (abaterii): se readoptă, valoarea de referință, R₀ = 530 MPa, și se vor parcurge etapele b. ( t_st = = 1,5403, t-value = = 0,0729; fig.2.50,b) și d.; ținând cont că, t_st < t_1-0,05 (1,5403 < 1,7613) sau t-value > α (0,0729 > 0,05), ipoteza de nul H₀ este admisă (caz neacceptabil din punct de vedere al ipotezei de cercetare). Astfel, în vederea aproprierii de nivelul de semnificație (5%) se continuă testul: se readoptă, valoarea de referință, R₀ = 527,5 MPa, și se vor parcurge etapele b. ( t_st = = 1,7809, t-value = = 0,0483; fig.2.50,c) și d.; deoarece, t_st > t_1-0,05 (1,7809 > 1,7613) sau t-value > α (0,0483 < 0,05), ipoteza de nul H₀ este respinsă, fiind semnificativă statistic cu probabilitatea t-value = 0,0483 (4,83%) mult apropriată de nivelul de semnificație α = 0,05 (5%); se acceptă ipoteza alternativă H₁ ( adică piesele lotului cu R > 227,5 MPa cedează prin rupere cu probabilitatea (certitudinea) de 95%.

Interpretări

Distribuția STUDENT(t) depinde de numărul de valori ale eșantionului și se aplică, cu precădere, pentru cercetările experimentale care au numărul n < 30 (v.subcap.2.4.2.3). Deci, pentru determinarea valorii funcției statistice student (distribuția t), z_st, corespunzătoare valorii de referință R₀ se va lua în considerare numărul de valori ale eșantionului n prin intermediul gradului de libertate, df = n-1, care reprezintă numărul de valori care pot varia pentru a se menține media m (de ex. pentru un set de date cu 15 valori, doar 14 (df = 14, fig. 2.50) pot varia pentru a se menține media 546 MPa).

Pentru adoptarea ipotezei alternative, R > R₀, s-a ținut cont de ipoteza de cercetare: verificarea rezistenței de cedare prin rupere. În urma studiului de mai sus se poate concluziona că pentru valori ale rezistenței la rupere R > R₀ = 527,5 MPa există posibilitatea de cedare a pieselor lotului prin rupere cu probabilitaea 95%.

a

b c

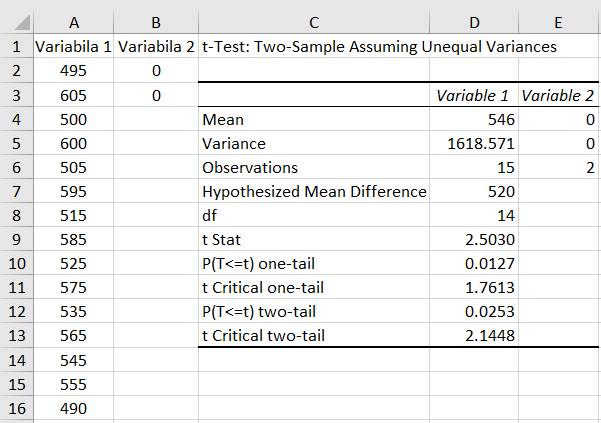
Fig. 2.50 Tabele cu valori ale datelor: a – valori măsurători și parametrii testului t cu valoarea de referință R₀ = 520 MPa; b – valori parametrii testului t cu valoarea de referință, R₀ = 530 MPa; c – valori parametrii testului t cu valoarea de referință, R₀ = 527,5 MPa

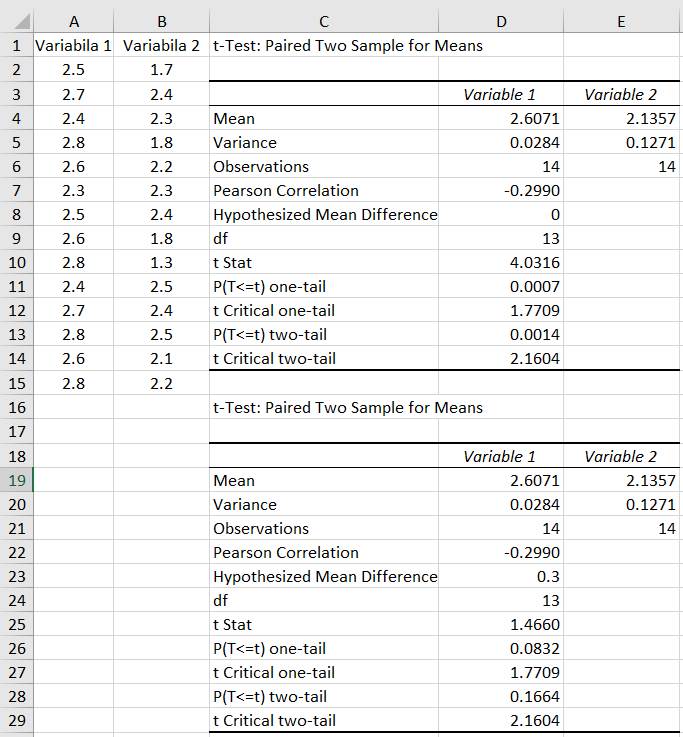
Fig. 2.51 Schemă asociată testului

2.5.5.6.3 Aplicație t-test de medie pentru două variabile pereche (dependente)

Ap.2.13 Să se determine presiunea medie a unui fluid dintr-o conductă prin măsurarea acesteia de către doi operatori, cu același instrument, în puncte diferite și în aceași perioadă de timp. Datele obținute (în urma măsurătorilor), două seturi cu câte 14 valori (coloanele A și B din fig. 2.52), se pot împerechea una câte una (Ghid.Ap.2.13).

Descrierea problemei statistice:

- definirea populației: valorile posibile ale presiunii din conducă; nu se cunosc parametrii µ, σ;

- nivelul de semnificație: α = 0,05 (5%); nivelul de încredere, p = 1-α = 0,95 (95%);

- volumul eșantioanelor: n = 14 valori fiecare (coloanele A și B din fig.2.52);

- caractersistica (proprietatea) de interes, variabila aleatoare: presiunea, p;

- parametrii de interes: mediile m₁, m₂; presiunile p_m1, p_m2;

- funcția statistică: STUDENT(t);

- tipul testului: testul t, deoarece volumul eșantionului n < 30.

Rezolvarea testului

Semnificații

Personalizarea algoritmului general (v.subcap. 2.5.5.5)

a. Formularea ipotezelor

Ipoteza de nul, H0	Ipoteza alternativă, H1	Denumire test
pm1 - pm2 = p0	pm1 - pm2 ≠ p0	Bilateral (two tail, două cozi), fig.2.53

Valoarea de referință a variabilei, p₀ = 0 (arată că presiunle medii sunt egale statistic).

b. Adoptarea funcției statistice (FS) și determinarea valorii acesteia și a semnificației statistice asociată: STUDENT(t); din ecuația STUDENT(t) = p₀, rezultă valoarea statistică; se determină cu funcția, din modul Excel Data Analysis și se obține t_st = = 4,0316 (fig. 2.53); semnificația statistică asociată, t-value, se determină cu opțiunea, din modul Excel Data Analysis și se obține

t-value = = 0,014.

c. Determinarea valorii critice: t_α/2 pentru α = 0,05; se determină cu funcția din Data Analysis, t_0,05/2 = = 2,1604 (fig.2.53).

d. Concluzia (decizia) privind acceptarea/respingerea ipotezei de nul (H₀): prin compararea valorii statistice t_st cu valori critice t_0,05/2/t_1-0,05/2 sau t-value cu α/2 se obțin: t_st > t_1-0,05/2 (4,0316 > 2,1604) ipoteza de nul H₀ este respinsă (fig.2.53,a) și se acceptă ipoteza alternativă H₁ care este admisă fiind semnificativă statistic cu probabilitatea p = 0,95 (95%); la aceași decizie se poate ajunge și ținând cont de inegalitatea, t-value < α/2 (0,014 < 0,025) (fig.2.53,a).

Obs. Luarea deciziei pentru cazurile bilaterale (cu două cozi) se ia ținând cont de una din cele două situații posibile corespunzătoare uneia dintre cozi

Interpretări

Pentru a evidenția că în urma măsurătorilor se obțin valori ale presiunilor medii egale (statistic), ipoteza de nul H₀ statuează că nu sunt diferențe între presiunile medii ale celor două eșantioane,

deci, p_m1 = p_m2 , și fiind perechi se va considera diferența, p_m1 - p_m2 = 0, deci cu variabila de referință, p₀ = 0; ipoteza alternativă (H₁) p_m1 - p_m2 ≠ 0 (p _m1 < p _m2 sau p _m1 > p _m2). Ipoteza de nul, H₀, se respinge și deci sunt diferențe semnificative (cu probabilitatea 95% sau riscul 5%) între valorile medii p_m1 = 2,0671 MPa și p_m2 = 2,1357 ale celor două eșantioane obținute prin măsurări diferite. Astfel, este contrazisă ipoteza de cercetare (asociată ipotezei alternative) și nu se poate trage concluzia că presiunile în domeniul (p_m1, p_m2) nu pot fi considerate ca fiind presiunea medie a fluidului. Deci, practic, pentru determinarea presiunii medii din conductă nu este nevoie de două seturi de măsurători, rezultatul oricărei măsurători se poate considera relevant cu certitudinea 95,5%.

Pe de altă parte, dacă ipoteza H₀ se va considera cu valoarea de referință p₀ = 0,3 (p_m1 - p_m2 = 0,3) și ipoteza alternativă, p_m1 - p_m2 ≠ 0,3 din analiza datelor obținute după aplicarea funcției din modulul Excel Data Analysis (al doilea set de date din fig. 2.52), consecință a inegalității t_st < t_1-0,05/2 (1,466 < 2,1604) sau t-value > α/2 (0,1664 < 0,025), rezultă că ipoteza de nul H₀ este acceptată (fig. 2.53,b) și deci se poate considera ca presiunea medie a fluidului din conductă poate fi în domeniul (p_m1, p_m2) când p_m1 - p_m2 = 0,3, având nivelul de semnificatie (risc) de 0,05 (5%). Deci, practic, pentru determinarea presiunii medii din conductă sunt necesare două seturi de măsurători, caz ineficient.

Distribuția STUDENT (t) depinde de numărul de valori ale eșantionului n < 30 (v.subcap.2.4.2.3). Deci, pentru determinarea valorii funcției statistice STUDENT (distribuția t), z_st, corespunzătoare valorii de referință p₀, se va lua în considerare numărul de valori ale eșantionului n prin intermediul gradului de libertate, df = n-1, numărul de valori care pot varia pentru a se menține media m (de ex. pentru un set de date cu 14 valori, doar 13 (df = 13, fig. 2.53) pot varia pentru a se menține media

Fig. 2.52 Tabel cu valori ale datelor, indicatorilor și parametrilor statistici

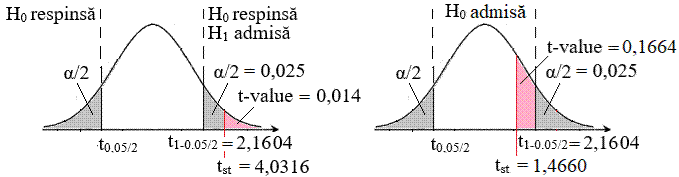
a b

Fig. 2.53 Scheme asociate testului: a – varianta ipotezei de nul respinsă; b – varianta ipotezei de nul acceptată

2.5.5.6.4 Aplicație t-test de medie pentru două variabile nepereche (independente) cu dispersiile egale

Ap.2.14 Presiunea medie a unui fluid dintr-o conductă se poate determina prin măsurarea acesteia de un singur operator, cu același instrument, într-un singur punct de lucru la perioade de timp diferite (de ex. dimineața și seara). Se poate afirma că presiunile medii măsurate sunt aceleași din punct de vedere statistic (ipoteza de cercetare) cu nivelul de semnificație (risc), α = 0,05 ? Datele obținute (în urma măsurătorilor), sunt grupate în două seturi cu câte 15 și 13 valori (coloanele A și, respectiv, B din fig. 2.54); cele două seturi de valori nu se pot împerechea una cate una (Ghid.Ap.2.14).

Descrierea problemei statistice:

- definirea populației: valorile posibile ale presiunii din conducă; nu se cunosc parametrii µ, σ;

- nivelul de semnificație: α = 0,05 (5%); nivelul de încredere, p = 1-α = 0,95 (95%);

- volumul eșantioanelor: n₁ = 15 valori, n₂ = 13 valori (coloanele A și B din fig.2.54);

- caractersistica (proprietatea) de interes, variabila aleatoare: presiunea, p;

- parametrul de interes; mediile m₁, m₂; presiunile p_m1, p_m2;

- funcția statistică: STUDENT(t);

- tipul testului: testul t, deoarece volumul eșantionului, n < 30.

Rezolvarea testului

Semnificații

Personalizarea algoritmului general (v.subcap. 2.5.5.5)

a. Formularea ipotezelor

Ipoteza de nul, H0	Ipoteza alternativă, H1	Denumire test
pm1 - pm2 = p0	pm1 - pm02 > p0 sau pm1 - pm02 < p0	Unilateral dreapta (right one-tail), sau Unilateral stânga (left one-tail),

Valoarea de referință a variabilei, p₀ = 0.

Obs. Se adoptă două variante pentru ipoteza alternativă deoarece, la început, nu se cunoaște care din ele este posibil să se întâmple.

b. Adoptarea funcției statistice (FS) și determinarea valorii acesteia și a semnificației statistice asociată: STUDENT(t); din ecuația STUDENT(t) = p₀, rezultă valoarea statistică; se determină cu funcția, din modul Excel Data Analysis, se obține t_st = = 1,8963; semnificația statistică asociată, t-value, se determină funcția, din modul Excel Data Analysis, se obține

t-value = = 0,0345 (fig. 2.57).

c. Determinarea valorii critice: t_α pentru α = 0,05; se determină cu funcția din Data Analysis, t_0,05 = = 1,7056 (fig.2.53).

e. Concluzia (decizia) privind acceptarea/respingerea ipotezei de nul (H₀): prin compararea valorii statistice t_st cu valori critice t_0,05/2/t_1-0,05/2 sau t-value cu α/2 se obțin: t_st > t_0,05 (1,8963 > 1,7056) ipoteza de nul H₀ este respinsă (fig.2.54) și se acceptă ipoteza alternativă H₁ (testul unilateral dreapta) fiind semnificativă statistic cu probabilitatea p = 0,95 (95%); aceași decizie se poate lua și ținând cont de inegalitatea, t-value < α (0,0345 < 0,005) (fig.2.54)

Interpretări

Verificarea îndepliniri ipotezei preliminare privind egalitatea dispersiilor: valorile dispersiilor (Variance, fig. 2.54) sunt cvasiiegale (0,0264 ≈ 0,0241) și, deci se respectă condiția cerută de testul t folosit ().

Obs. Dacă în urma aplicării funcției rezultată valori diferite ale dispersiilor (Variance) se va folosi funcția din modulul Excel Data Analysis.

În final, dacă ipoteza de nul (H₀) este respinsă (p_m1 - p_m2 = 0, nu este adevărată) și se admite ipoteza alternativă (H1), p_m1 - p_m2 > 0 (p_m1 > p_m2) se poate concluziona că la nivel de populație (valori posibile ale presiunii), ipoteza de cercetare (cum că presiunile medii măsurate la perioade de timp diferite sunt aceleași) NU este verificată și deci conform testului presiunea medie măsurată dimineața este mai mare ca presiunea medie măsurată seara.

Distribuția STUDENT(t) depinde de numărul de valori ale eșantionului n < 30 (v.subcap.2.4.2.3). Deci, pentru determinarea valorii funcției statistice STUDENT(t), t_st, corespunzătoare valorii de referință p₀ se va lua în considerare numerele de valori al eșantioanelor prin intermediul gradului de libertate, df = n₁-1 + n₂-1, numărul de valori care pot varia pentru a se menține media (de ex. pentru seturile de date cu 15 și 13 valori, doar 26 (df = 26, fig. 2.54) pot varia pentru a se menține media)

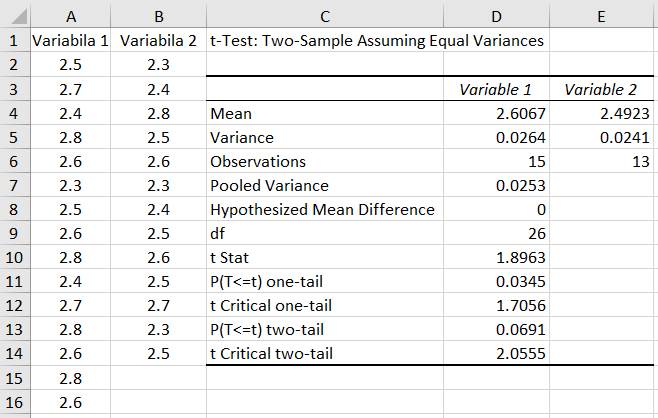
Fig. 2.53 Tabel cu valori ale datelor, indicatorilor și parametrilor statistici

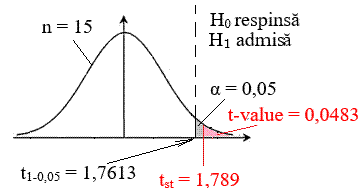
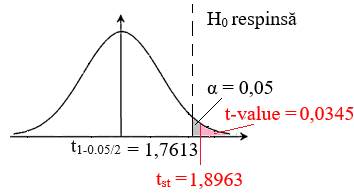
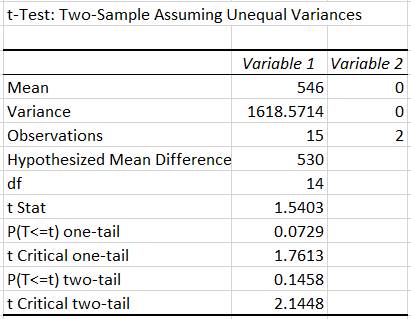
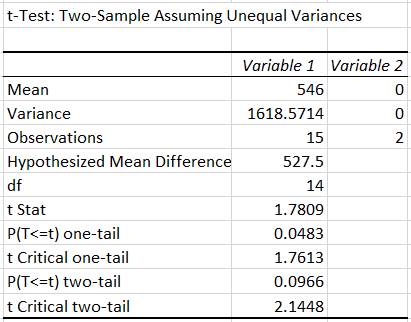
Fig. 2.54 Schemă asociată testului

2.5.5.6.5 Aplicație t-test de medie pentru două variabile nepereche (independente) cu dispersii inegale

Ap.2.15 Presiunea medie a unui fluid dintr-o conductă se poate determina prin măsurarea acesteia de doi operatori, cu același instrument, în puncte diferite la perioade de timp diferite (de ex. dimineața și seara). Se poate afirma că presiunile medii măsurate sunt diferite din punct de vedere statistic (ipoteza de cercetare) cu nivelul de semnificație (risc), α = 0,05 ? Datele obținute (în urma măsurătorilor), sunt grupate în două seturi cu câte 15 și 11 valori (coloanele A și, respectiv, B din fig. 2.55), NU se pot împerechea una câte una (Ghid.Ap.2.15).

Descrierea problemei statistice:

- definirea populației: valorile posibile ale presiunii din conducă; nu se cunosc parametrii µ, σ;

- nivelul de semnificație: α = 0,05 (5%); nivelul de încredere, p = 1-α = 0,95 (95%);

- volumul eșantioanelor: n₁ = 15 valori, n₂ = 11 valori (coloanele A și B din fig.2.55);

- caractersistica (proprietatea) de interes, variabila aleatoare: presiunea, p;

- parametrul de interes; mediile m₁, m₂; presiunile p_m1, p_m2;

- funcția statistică: STUDENT(t);

- tipul testului: testul t, deoarece volumele eșantioanelor, n < 30.

Rezolvarea testului

Semnificații

Personalizarea algoritmului general (v.subcap.2.5.5.5)

a. Formularea ipotezelor

Ipoteza de nul, H0	Ipoteza alternativă, H1	Denumire test
pm1 - pm2 = p0	pm1 - pm02 ≠ p0	Bilateral (two tail, două cozi), fig.2.56

Valoarea de referință a variabilei, p₀ = 0.

b. Adoptarea funcției statistice (FS) și determinarea valorii acesteia și a semnificației statistice asociată: STUDENT(t); din ecuația STUDENT(t) = p₀, rezultă valoarea statistică; se determină cu funcția, din modul Excel Data Analysis, se obține t_st = = 4,0835; semnificația statistică asociată, t-value, se determină funcția, din modul Excel Data Analysis, se obține, t-value = = 0,0013 (fig. 2.54).

c. Determinarea valorii critice: t_α/2 pentru α = 0,05; se determină cu funcția din modulul Excel Data Analysis, t_0,05/2 = = 2,1604 (fig.2.54).

d. Concluzia (decizia) privind acceptarea/respingerea ipotezei de nul (H₀): prin compararea valorii statistice t_st cu valorea critică t_0,05/2/t_1-0,05/2: t_st > t_1-0,05/2 (4,0835 > 2,1604) ipoteza de nul H₀ este respinsă și se acceptă ipoteza alternativă H₁ (testul bilateral) ca fiind semnificativ statistic cu probabilitatea p = 0,95 (95%); aceași decizie se poate lua și ținând cont de inegalitatea: t-value < α (0,0013 < 0,025) (fig.2.56)

Interpretări

Verificarea îndepliniri ipotezei preliminare privind inegalitatea dispersiilor:valorile dispersiilor (Variance, fig. 2.55) sunt inegale (0,0264 ≠ 0,15) și, deci se respectă condiția cerută de testul t folosit ().

Obs. Dacă în urma aplicării funcției rezultată valori cvasiegale ale dispersiilor (Variance) se va folosi funcția din modulul Excel Data Analysis.

În final, dacă ipoteza de nul (H₀) este respinsă (p_m1 - p_m2 = 0, nu este adevărată) și se admite ipoteza alternativă (H1), p_m1 - p_m2 ≠ 0 (p_m1 ≠ p_m2) se poate concluziona că la nivel de populație (valori posibile ale presiunii), ipoteza de cercetare (cum că presiunile medii măsurate la perioade de timp diferite NU sunt aceleași) este verificată și deci conform testului presiunea medie măsurată dimineața este mai mare ca presiunea medie măsurată seara).

Distribuția STUDENT(t) depinde de numărul de valori ale eșantionului n < 30 (v.subcap.2.4.2.3). Deci, pentru determinarea valorii funcției statistice STUDENT, t_st, corespunzătoare valorii de referință p₀ se va lua în considerare numerele de valori al eșantioanelor prin intermediul gradului de libertate, df = (n₁ + n₂)/2 , numărul de valori care pot varia pentru a se menține media (de ex. pentru seturile de date cu 15 și 11 valori, doar 13 (df = 13, fig. 2.55) pot varia pentru a se menține media

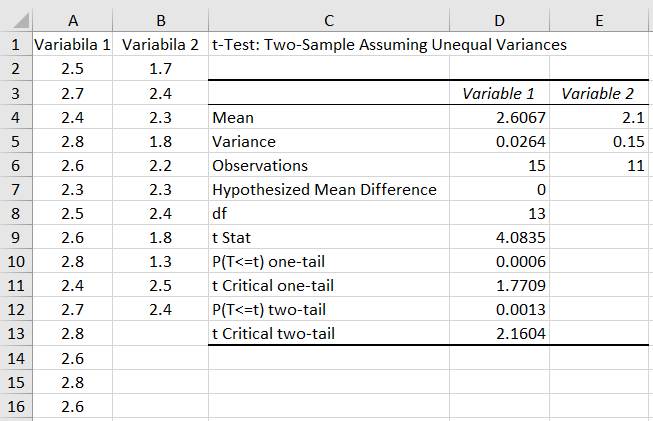
Fig. 2.55 Tabel cu valori ale datelor, indicatorilor și parametrilor statistici

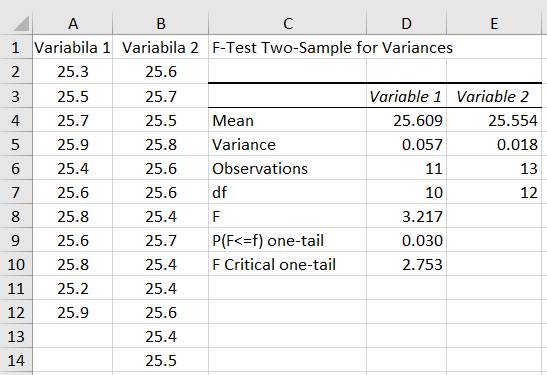
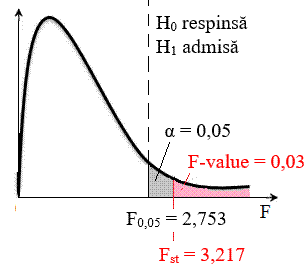
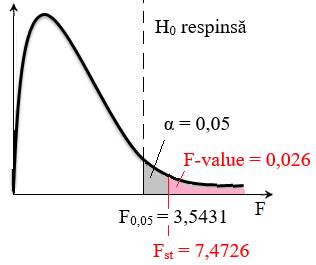
Fig. 2.56 Schemă asociată testului

2.5.5.6.6 Aplicație testul F de dispersie pentru două variabile

Ap.2.16 Să se verifice că în urma modificării unei instalații experimentale datele obținute prin măsurători s-au îmbunătățit din punct de vedere statistic, fiind mai grupate în jurul mediei pentru varianta îmbunătățită. Astfel, se va compara dispersia setului de date, variabila 1 (coloana A, fig. 2.57), obținute cu instalația experimentală inițială, cu dispersia setului de date, variabila 2 (coloana B, fig. 2.57) obținute cu instalația experimentală modificată (Ghid.Ap.2.16).

Descrierea problemei statistice:

- definirea populației: valorile posibile ale măsurătorilor; nu se cunosc parametrii µ, σ;

- nivelul de semnificație: α = 0,05 (5%); nivelul de încredere, p = 1-α = 0,95 (95%);

- volumul eșantioanelor: n₁ = 11 valori, n₂ = 13 valori (coloanele A și B din fig.2.57);

- caractersistica (proprietatea) de interes, variabila aleatoare: valori obținute prin măsurare, u;

- parametrul de interes; dispersiile, , ;

- funcția statistică: FISHER;

- tipul testului: testul F.

Rezolvarea testului

Semnificații

Personalizarea algoritmului general (v.subcap.2.5.5.5)

e. Formularea ipotezelor

Ipoteza de nul, H0	Ipoteza alternativă, H1	Denumire test
= ( - = )	> ( - > )	Unilateral dreapta (right one-tail), fig.2.58

Valoarea de referință a dispersiei, = 0.

f. Adoptarea funcției statistice (FS) și determinarea valorii acesteia și a semnificației statistice asociată: FISHER; din ecuația FISHER(s²) = ), rezultă valoarea statistică; se determină cu funcția, din modul Excel Data Analysis, se obține, F_st = F = 3,217 (fig. 2.57); semnificația statistică asociată, F-value, se determină funcția, din modul Excel Data Analysis, se obține, F-value = = 0,03 (fig. 2.57).

g. Determinarea valorii critice: F_α pentru α = 0,05; se determină cu funcția din modulul Excel Data Analysis, F_0,05 = = 2,753 (fig.2.57).

h. Concluzia (decizia) privind acceptarea/respingerea ipotezei de nul (H₀): prin compararea valorii statistice F_st cu valorea critică F_0,05: F_st > F_0,05 (3,217 > 2,753) ipoteza de nul H₀ este respinsă și se acceptă ipoteza alternativă H₁ ca fiind semnificativă statistic cu probabilitatea p = 0,95 (95%); aceași decizie se poate lua și ținând cont de inegalitatea: F-value < α (0,03 < 0,05) (fig.2.58)

Interpretări

În final, dacă ipoteza de nul (H₀) este respinsă ( - = 0, nu este adevărată) și se admite ipoteza alternativă (H1), - > 0 (0,057 > 0,018) adică dispersia setului de date obținut cu instalația experimentală modificată are disperia, s²₂ = 0,018, mai mică (îmbunătățită) decât dispersia setului de date obținut cu instalația experimentală inițială s²₁ = 0,057 cu probabilitatea de 95%

Pentru determinarea valorii funcției statistice Fischer, F_st, corespunzătoare valorii de referință se va lua în considerare numărul de valori al eșantioanelor n₁ și n2 prin intermediul gradelor de libertate, df₁ = n₁ -1 = 10 și df₂ = n₂ -1 = 12.

Obs. Utilizare t-test și F-test: t-test este utilizat pentru a determina dacă există sau nu o diferență semnificativă între mediile a două seturi de date, F – test este utilizat pentru compararea a două seturi de date din punct de vedere al dispersiilor (sânt sau nu egale)

Fig. 2.57 Tabel cu valori ale datelor, indicatorilor și parametrilor statistici

Fig. 2.58 Schemă asociată testului

2.5.5.6.7 Aplicație ANOVA cu un singur factor (one-way ANOVA, Single Factor)

ANOVA este un modul software integrat pachetul Microsoft Excel care detectează diferențele dintre seturi de date, cu precădere, legate de mediile acestora când există una sau două variabile dependente parametric și una sau mai multe variabile independente; ANOVA compară mediile a mai mult de două seturi de date (variabile aleatorii) spre deosebire de testul t care compară numai două. 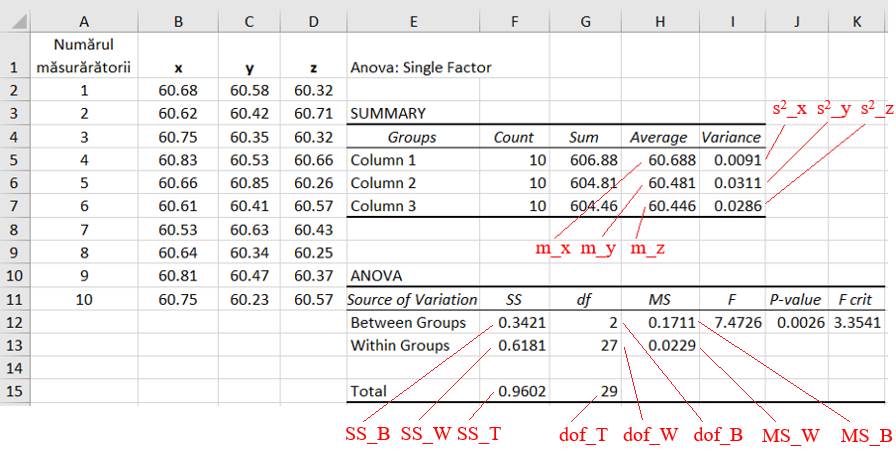Tipuri de module ANOVA: One Way ANOVA (one dependent variable, one independent variable), Two Way ANOVA (two dependent variable, two ore more independent variables)

Ap.2.17 Să se compare statistic seturile de date (x, y, z; coloanele B, C, D din fig.2.59) asociate măsurătorilor aceluiași parametru fizic oarecare (de ex. …), dar în condiții de mediu diferite (de ex. la 3 temperaturi diferite) (Ghid.Ap.2.17).

Descrierea problemei statistice:

- definirea populației: valorile posibile ale măsurătorilor; nu se cunosc parametrii µ, σ;

- nivelul de semnificație: α = 0,05 (5%); nivelul de încredere, p = 1-α = 0,95 (95%);

- volumele eșantioanelor: n_x = 9 valori, n_y = 9 valori, n_z = 9 valori (coloanele B, C și D din fig.2.59);

- caractersistica (proprietatea) de interes, variabila aleatoare: valori obținute prin măsurare, cu distribuție normală (m, s);

- parametrul de interes: mediile m_x, m_y, m_z; dispersiile s²_x, s²_y, s²_z;

- funcția statistică: FISCHER;

- tipul testului: ANOVA.

Rezolvarea testului

Semnificații

Personalizarea algoritmului general (v.subcap.2.5.5.5)

a. Formularea ipotezelor

Ipoteza de nul, H0	Ipoteza alternativă, H1	Denumire test
m_x = m_y = m_z	m_x ≠ m_y ≠ m_z	ANOVA unilateral dreapta (right one-tail), fig.2.60

b. Adoptarea funcției statistice (FS) și determinarea valorii acesteia și a semnificației statistice asociată: FISHER; din ecuația FISHER(F) = 0, rezultă valoarea statistică; se determină cu funcția, din modul Excel Data Analysis, F_st = F = 7,4726 (fig. 2.59); semnificația statistică asociată, F-value, se determină funcția, din modulul Excel Data Analysis, F-value = P-value = 0,026 (fig. 2.59).

c. Determinarea valorii critice: F_α pentru α = 0,05; se determină cu funcția din modulul Excel Data Analysis, F_0,05 = Fcrit = 3,3541 (fig.2.59).

Obs. p-value (F-value) se poate determina și cu funcția Excel F.DIST; Fcrit se poate calcula și cu funcția Excel F.INV.

d. Concluzia (decizia) privind acceptarea/respingerea ipotezei de nul (H₀): prin compararea valorii statistice F_st cu valorea critică F_0,05: F_st > F_0,05 (7,4726 > 3,5431) ipoteza de nul H₀ este respinsă și se acceptă ipoteza alternativă H₁ (există diferențe între mediile celor 3 seturi de date) ca fiind semnificativă statistic cu probabilitatea p = 0,95 (95%); aceași decizie se poate lua și ținând cont de inegalitatea: F-value < α (0,026 < 0,05) (fig.2.60)

Interpretări

Tabelul SUMMARY conține date statistice:

Liniile din coloana Groups: Column 1, reprezintă, variabila x; Column 2 – variabila y; Column 3 – variabila z;

Coloana Count reprezintă numărul total al măsurătorilor, j = 10.

Coloana Sum:

Sum_x = 606,688, suma valorilor variabilei x,

Sum_y = 604,81, suma valorilor variabilei y;

Sum = Sum_z = 604,46, suma valorilor variabilei z.

Coloana Average, reprezintă mediile valorilor variabilelor x, y, z: m_x = 60,688; m_y = 60,481; m_z = 60,466;

Coloana Variance, reprezintă dispersiile variabilelor x, y, z: s²_x = 0,091; s²_y = 0,0311; s²_z = 0,0286.

Tabelul ANOVA conține date statistice de decizie privind comportamentul statistic la nivel de factorii independenți Op1, Op2 (Sample), dependenți m_x, m_y, m_z (Columns) și interdependențe dintre aceștia (Interaction):

Coloana SS (Sum Squares, suma pătratelor abaterilor față de diverse valori de medie) permite cuantificarea dispersiei (variabilității) și are trei forme: la nivel global (SS_T), în interiorul seturilor de date (SS_W) și între seturile de date (SS_B) între care există relația, SS_T = SS_W + SS_B, unde,

SS_B = + + ) = 0,3421 (Sum Square_Between), suma pătratelor abaterilor mediilor variabilelor (m_x, m_y, m_z) față de media tuturor valorilor variabilelor, m; valorea SS_B indică cât din disperaia totală este din cauza dispersiilor seturilor de date (“Between”);

SS_W = + + ) = 0,6181 (Sum Square_Within), suma pătratelor abaterilor valorilor variabilelor (x, y, z) față de mediile variabilelor (m_x, m_y, m_z); valoarea SS_W indică cât din disperaia totală este din cauza dispersiilor din interiorul seturilor de date (“Wthin”);

SS_T = + + ) = 0,9602 (Sum Square_Total), suma pătratelor abaterilor valorilor variabilelor (x, y, z) față de media tuturor valorilor variabilelor, m.

Deci, vavorile SS_W și SS_B evidențiază cât din valoarea SS_T se datorează variației dispersiilor din interiorul fiecărui set (“Wthin”) și, respective, variației dispersiilor seturilor de date (“Between”).

Coloana dof (grade de libertate):

dof_B = k -1 = 2, pentru calculul SS_B, unde k = 3 numărul variabilelor (seturilor) aleatorii;

dof_W = k (j-1) = 3 (10 -1) = 27, pentru calculul SS_W, unde j = 10, numărul valorilor variabilelor;

dof_T = j k -1 = 10*3 – 1 = 29, pentru calculul SS_T;

dof_x = j -1, dof_y = j -1, dof_z = j -1;

Verificare: dof_B + dof_W = dof_T.

Dispersia, s² = .

Coloana MS (Mean Square), reprezintă media pătratelor dispersiilor (variabilităților) și se determină în interiorul seturilor de date MS_W (Mean Square_Within) și între seturile de date MS_B ( Mean Square_Between) cu relațiile:

MS_B = SS_B/dof_B = 0,3421/2 = 0,1711,

MS_W = SS_W/dof_W = 0,6181/27 = 0,0229.

Coloana F (funcția statistică):

F = MS_B/MS_W = 0,1711/0,0229 = 7,4726 valoarea funcției statistice FISCHER.

Obs. testul ANOVA varianta single factor (one-way) nu indică care set de date este senificativ diferit dintre seturile analizate; deoarece testul ANOVA respinge ipoteza de egalitate a mediilor (H₀) deci a mediilor temperaturilor; deoarece, nu se precizează care grupuri au mediile diferite se va performa analiza post-hoc care evidențiază seturile care diferă ca medie.

Fig. 2.59 Tabel cu valori ale datelor, indicatorilor și parametrilor statistici

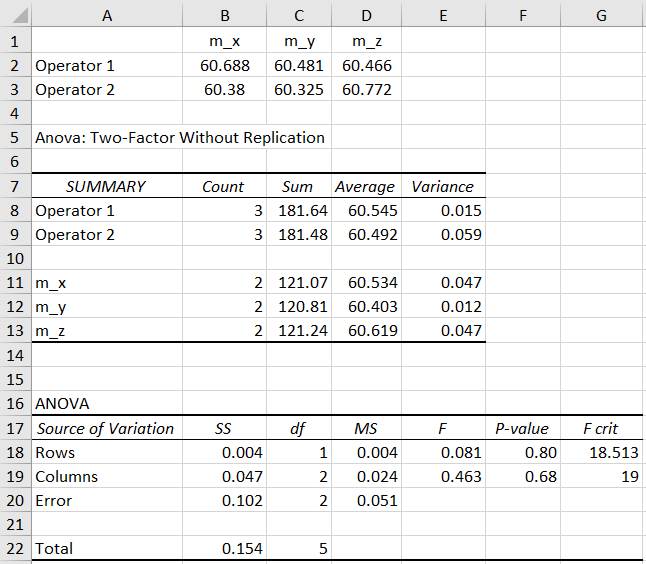
Fig. 2.60 Schemă asociată testului

2.5.5.6.8 Aplicație testul ANOVA cu doi factori fără replicație (ANOVA: Two-Factor Without Replication)

Ap.2.18 Să se compare statistic seturile de măsurători ale unui parametru fizic corespunzătoare seturilor (variabilelor) x, y, z cu mediile m_x, m_y, m_z (coloanele B, C, D din fig.2.61) efectuate de 2 operatori (Operator 1, Operator 2) dar în condiții de mediu diferite (de ex. x, y, z pot fi corespunzătoare a trei temperaturi diferite) (Ghid.Ap.2.18).

Descrierea problemei statistice:

- definirea populației: valorile posibile ale măsurătorilor; nu se cunosc parametrii µ, σ;

- nivelul de semnificație: α = 0,05 (5%); nivelul de încredere, p = 1-α = 0,95 (95%);

- volumele seturilor de medii: m_x, m_y, m_z (coloanele B, C și D din fig.2.61);

- caractersistica (proprietatea) de interes, variabila aleatoare: valorile obținute prin măsurare;

- parametrul de interes: mediile m_x, m_y, m_z; dispersiile s²_x, s²_y, s²_z;

- funcția statistică: FISCHER;

- tipul testului: ANOVA cu doi factori fără replicație (doi operatori care efectuează 3 seturi de măsurători); implică o singură valoare a fiecărei variabile pentru ce doi factori: operatorii (Oprartor 1, Operator 2) în condiții de mediu diferite cu câte trei valori asociate.

Rezolvarea testului

Semnificații

Personalizarea algoritmului general (v.subcap.2.5.5.5)

a. Formularea ipotezelor

Ipoteza de nul, H0	Ipoteza alternativă, H1	Denumire test
H01: m_x = m_y = m_z; H02: m_Op1 = m_Op2	H11: m_x ≠ m_y ≠ m_z; H12: m_Op1 ≠ m_Op2	ANOVA: unilateral dreapta (right one-tail), fig.2.62

b. Adoptarea funcției statistice (FS) și determinarea valorii acesteia și a semnificației statistice asociată: FISHER; din ecuația FISHER(F) = 0, rezultă valoarea statistică; se determină cu funcția, din modul Excel Data Analysis și se obține (fig. 2.61):

F_st = F = 0,08, pentru Operator1 și Opeartor 2 (rows);

F_st = F = 0,463, pentru m_x, m_y și m_z (columns).

Semnificația statistică asociată, F-value, se determină funcția, din modul Excel Data Analysis(fig. 2.61):

F-value = P-value = 0,80, pentru Operator1 și Opeartor 2 (rows);

F-value = P-value = 0,463, pentru m_x, m_y și m_z (columns).

c. Determinarea valorii critice, F_α pentru α = 0,05: se determină cu funcția din modulul Excel Data Analysis (fig.2.61):

F_0,05 = Fcrit = 18,513, pentru Operator 1 și Opeartor 2 (rows);

F_0,05 = Fcrit = 19, pentru m_x, m_y și m_z (columns).

d. Concluzii (decizii) privind acceptarea/respingerea ipotezelor de nul, prin compararea valorilor statistice F_st cu valorea critică F_0,05:

- F_st < F_0,05 (0,081 < 18,513), pentru Operator1 și Opeartor 2 (rows), ipoteza de nul H₀₁ este acceptată (NU există diferențe semnificative între mediile celor corespunzătoare factorilor Operator 1 și Operator 2) cu probabilitatea p = 0,95 (95%); aceași decizie se poate lua și ținând cont de inegalitatea: F-value > α (0,80 > 0,05) (fig.2.62,a).

- F_st < F_0,05 (0,463 < 19), pentru m_x, m_y și m_z (columns), ipoteza de nul H₀₂ este acceptată (NU există diferențe semnificative între mediile celor corespunzătoare factorilor m_x, m_y și m_z) cu probabilitatea p = 0,95 (95%); aceași decizie se poate lua și ținând cont de inegalitatea: F-value > α (0,68 > 0,05) (fig.2.62,b)

Interpretări

Tabelul SUMMARY (fig. 2.61)conține date statistice:

Coloana Count reprezintă numărul total al valorilor mediilor măsurătorilor: j = 3, pentru Operator 1 și Operator 2); k = 2, pentru mediile m_x, m_y și m_z.

Coloana Sum (fig. 2.61)

Sum_Op1 = 181,64, suma valorilor mediilor m_x_op1, m_y_Op1, m_z_Op1;

Sum_Op2 = 181,48, suma valorilor variabilei suma valorilor mediilor m_x_Op2, m_y_Op2, m_z_Op2;

Sum_x = 121,87, suma valorilor mediilor m_x;

Sum_y = 120,81, suma valorilor mediilor m_y;

Sum_z = 121,24, suma valorilor mediilor m_z.

Coloana Average (fig. 2.61)

Average_Op1 = 60,545, media mediilor m_x_Op1 m_y_Op1, m_z_Op3;

Average_Op2 = 60,545, media mediilor m_x_Op2, m_y_Op2, m_z_Op2;

Average_x = 60,534, media mediilor m_x;

Average_y = 60,403, media mediilor m_y;

Average_x = 60,614, media mediilor m_z.

Coloana Variance (fig. 2.61)

Variance_Op1 = 0,015, dispersia mediilor mediilor m_x_Op1 m_y_OP1, m_z_Op1;

Variance_Op2 = 0,059, dispersia mediilor mediilor m_x_Op2 m_y_Op2, m_z_Op2;

Variance_x = 0,47, dispersia mediilor m_x_OP1, m_x_OP1;

Variance_y = 0,12, dispersia mediilor m_y_Op1, m_y_Op1;

Variance_x = 0,47, dispersia mediilor m_z_Op1, m_z_Op1.

Tabelul ANOVA conține date statistice care permit luarea de decizii privind comportamentul statistic la nivel de factorii independenți Op1, Op2 (Sample), dependenți m_x, m_y, m_z (Columns) și interdependențe dintre aceștia (Interaction):

Coloasna SS (Sum Squares, suma pătratelor abaterilor față de diverse valori de medie) permite cuantificarea dispersiei (variabilității) la nivel global (SS_Total), de operatori (SS_Rows) și dependent de variabile x, y, z (SS_Columns):

SS_Rows = + + ) + + + ) = 0,04; valorea SS_Rows indică cât din disperaia totală este din cauza dispersiilor seturilor de date asociate operatorilor;

SS_Columns = + + + + + = 0,047; valorea SS_Coloumns indică cât din disperaia totală este din cauza dispersiilor asociate variabilelor x, y, z;

SS_Total = + + ) = 0,154, unde m este media tuturor valorilor variabilelor;

SS_Error = SS_Total - SS_Rows - SS_Columns = 0,154; această valoare este o măsură a dependenței (interacțiunilor) dispersiilor.

Coloana dof (grade de libertate):

dof_Rows = k -1 = 1,

dof_Columns = j - 1 = 3,

dof_Error = dof_Rows*dof_Columns = 2,

dof_Total = j*k -1 = 5.

Coloana MS (Mean Square), reprezintă media pătratelor dispersiilor (variabilităților) corespunzătoare operatorilor (MS_Rows), variablelor x, y, z (MS_Columns) și erorilor (MS_Error):

MS_Rows = SS_Rows/SS_Rows = 1,

MS_Columns = SS_Columns/ dof_Columns = 0,024,

MS_Error = SS_Error/ dof_Error = 0,051.

Coloana F (funcția statistică):

F_Rows = MS_Rows/MS_Error = 0,081,

F_Columns = MS_Columns/MS_Error = 0,463.

Coloana P-value (semnifcația statistică efectivă)

P-value_Rorws = 0,80, pentru Operator1 și Opeartor 2;

P-value_Columns = 0,463, pentru m_x, m_y și m_z.

Coloana F crit (semnificații statistice):

Fcrit_Rows = 18,513, pentru Operator1 și Opeartor 2;

Fcrit_Columns = 19, pentru m_x, m_y și m_z.

Obs. P-value (F-value) se poate determina și cu funcția Excel F.DIST.RV; F crit se poate calcula și cu funcția Excel F.INV.RT.

Ipotezele testelor ANOVA cu doi factori fără replicație:

- ipoteza de nul (H₀) pentru factorul A, NU ESTE semnificativă (mediile liniilor nu diferă semnificativ), ipoteza alternativă (H₁₁) pentru factorul A, ESTE semnificativă (mediile liniilor diferă semnificativ);

- ipoteza de nul (H₀) pentru factorul B, NU ESTE semnificativă (mediile coloanelor nu diferă semnificativ); ipoteza alternativă (H₁₂) pentru factorul B, ESTE semnificativă (mediile coloanelor diferă semnificativ).

Analiza dispersiilor bazat pe testul ANOVA cu doi factori fără replicație are ca scop evidențierea dispersiilor induse de de cei doi factori și de cele inexplicabile.

În urma analizei valorilor se evidențiază acceptarea ipotezei de nul (H₀) atât pentru mediile asociate variabilelor x, y, z (fig. 2.62,a) cât și pentru cele ale operatorilor (Opeartor 1, Operator 2) (fig. 2.62,b); astfel se evidențiază că valorile măsurătorilor x, y, z NU influențeză statistic, cu o probabilitatea 0,95 (95%), mediile măsurătorilor obținute de opeartori

Fig. 2.61 Tabel cu valori ale datelor, indicatorilor și parametrilor statistici

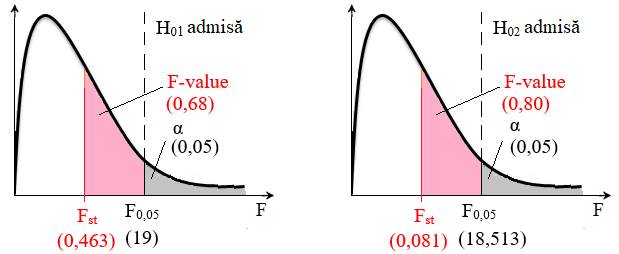
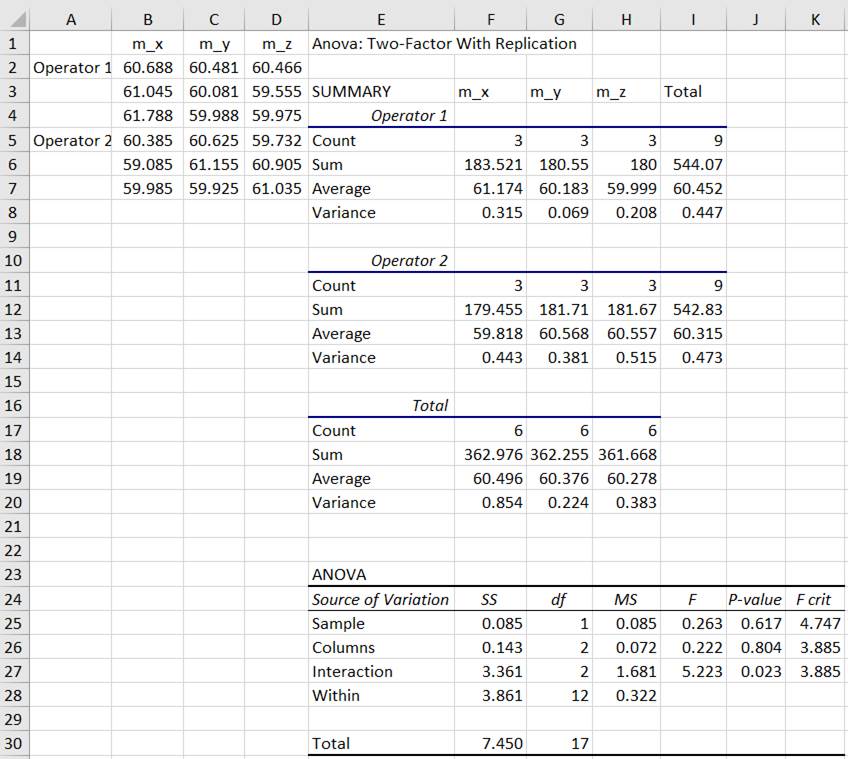
a b

Fig. 2.62 Scheme asociate ANOVA: a – varianta H₀₁ admisă; b – varianta H₀₂ admisă

2.5.5.6.9 Aplicație testul ANOVA cu doi factori cu replicație (ANOVA: Two-Factor with Replication)

Ap.2.19 Să se compare statistic seturile de măsurători ale unui parametru fizic corespunzătoare seturilor (variabilelor) x, y, z cu mediile m_x, m_y, m_z (coloanele B, C, D din fig.2.61) efectuate de 2 operatori (Operator 1, Operator 2) dar în condiții de mediu diferite (de ex. x, y, z pot fi corespunzătoare a trei temperaturi diferite) (Ghid.Ap.2.19).

Descrierea problemei statistice:

- definirea populației: valorile posibile ale măsurătorilor; nu se cunosc parametrii µ, σ;

- nivelul de semnificație: α = 0,05 (5%); nivelul de încredere, p = 1-α = 0,95 (95%);

- volumele seturilor de medii: m_x, m_y, m_z (coloanele B, C și D din fig.2.61);

- caractersistica (proprietatea) de interes, variabila aleatoare: valorile obținute prin măsurare;

- parametrul de interes: mediile m_x, m_y, m_z; dispersiile s²_x, s²_y, s²_z;

- funcția statistică: FISCHER;

- tipul testului: ANOVA cu doi factori cu replicație (doi operatori care efectuează câte 3 seturi de măsurători); implică câte trei valori ale fiecărei variabile pentru ce doi factori: operatorii (Operator 1, Operator 2) în condiții de mediu diferite cu câte trei valori asociate; există date pereche (replici) prin combinarea celor doi factori.

Rezolvarea testului

Semnificații

Personalizarea algoritmului general (v.subcap.2.5.5.5)

a. Formularea ipotezelor

Ipoteza de nul, H0	Ipoteza alternativă, H1	Denumire test
H01: m_x = m_y = m_z; H02: m_Op1 = m_Op2; H03: Nu există interdependențe între factori	H11: m_x ≠ m_y ≠ m_z; H12: m_Op1 ≠ m_Op2; H13: Există interdependențe între factori	ANOVA: unilateral dreapta (right one-tail), fig.2.64

b. Adoptarea funcției statistice (FS) și determinarea valorii acesteia și a semnificației statistice asociată: FISHER; din ecuația FISHER(F) = 0, rezultă valoarea statistică; se determină cu funcția, din modul Excel Data Analysis, se obține:

F_st = F = 0,263 (fig. 2.63), pentru factorii independenți (Op1, Op2; Sample);

F_st = F = 0,222 (fig. 2.63), pentru factorii dependenți (m_x, m_y, m_z; Columns);

F_st = F = 5,223 (fig. 2.63), pentru interdependențele dintre factorii independenți (Op1, Op2) și factorii dependenți (m_x, m_y, m_z);

Semnificația statistică asociată, F-value, se determină funcția, din modul Excel Data Analysis:

F-value = P-value = 0,617 (fig. 2.63), pentru factorii independenți (Op1, Op2; Sample);

F-value = P-value = 0,804 (fig. 2.63), pentru factorii dependenți (m_x, m_y, m_z; Columns);

F-value = P-value = 0,023 (fig. 2.63), pentru interdependențele dintre factorii independenți. (Operator 1, Operator 2) și factorii dependenți (m_x, m_y, m_z).

c. Determinarea valorii critice, F_α pentru α = 0,05; se determină cu funcția din modulul Excel Data Analysis:

F_0,05 = Fcrit = 4,747 (fig.2.63), pentru factorii independenți (Op1, Op2; Sample);

F_0,05 = Fcrit = 3,885 (fig.2.63), pentru factorii dependenți (m_x, m_y, m_z; Columns);

F_0,05 = Fcrit = 3,885 (fig.2.63), pentru interdependențele dintre factorii independenți (Op1, Op2) și factorii dependenți (m_x, m_y, m_z).

d. Concluzii (decizii) privind acceptarea/respingerea ipotezelor de nul, prin compararea valorii statistice F_st cu valorea critică F_0,05:

- F_st < F_0,05 (0,263 < 4,747), pentru factorii independenți (Op1, Op2; Sample), ipoteza de nul H₀₁ este acceptată (NU există diferențe semnificative între mediile corespunzătoare factorilor independenți (Op1, Op2; Sample) cu probabilitatea p = 0,95 (95%); aceași decizie se poate lua și ținând cont de inegalitatea: F-value > α (0,617 > 0,05) (fig.2.64,a).

- F_st < F_0,05 (0,222 < 3,885), pentru factorii dependenți (m_x, m_y, m_z; Columns), ipoteza de nul H₀₂ este acceptată (NU există diferențe semnificative între mediile corespunzătoare dependenți (m_x, m_y, m_z; Columns) cu probabilitatea p = 0,95 (95%); aceași decizie se poate lua și ținând cont de inegalitatea: F-value > α (0,804 > 0,05) (fig.2.64,b);

- F_st > F_0,05 (5,223 > 3,883), pentru interdependențele dintre factorii independenți (Op1, Op2) și factorii dependenți (m_x, m_y, m_z), ipoteza de nul H₀₃ este respinsă și se acceptă ipoteza alternativă H₁₃ (există diferențe semnificative între interdependențele dintre factorii independenți (Op1, Op2; Sample) și factorii dependenți (m_x, m_y, m_z; Columns) cu probabilitatea p = 0,95 (95%); aceași decizie se poate lua și ținând cont de inegalitatea: F-value < α (0,023 < 0,05) (fig.2.64,c)

Interpretări

Tabelul SUMMARY conține date statistice:

Liniile Count din tabelele Operator 1 și Operator 2, reprezintă numărul total al valorilor mediilor valorilor variabilelor (măsurătorilor), k = 3, pentru mediile m_x, m_y și m_z.

Liniile Sum din tabelele Operator 1 și Operator 2, reprezintă sumele valorilor mediilor m_x, m_y și m_z.

Liniile Average din tabelele Operator 1 și Operator 2, reprezintă mediile valorilor mediilor m_x, m_y și m_z.

Liniile Variance din tabelele Operator 1 și Operator 2, reprezintă dispersiile valorilor mediilor m_x, m_y și m_z.

Tabelul ANOVA conține date statistice care permit luarea de decizii privind comportamentul statistic la nivel de factorii independenți Operator 1, Operator 2 (Sample), dependenți m_x, m_y, m_z (Columns), interdependențe dintre aceștia (Interaction) și dispersiilor din interiorul seturilor de date (Wthin):

- linia Simple conține valorile asociate factorilor independenți (Operator 1, Operator 2): SS_Sample = 0,085; dof_Sample = 1; MS_Sample = SS_ Simple/dof_ Simple = 0,085; F_Simple = MS_Simple/MS_Width = 0,0847/0,3218 = 0,263; F_Simple < Fcrit_Sample (0,263 < 4,747); p-value_Sample > α (0,617 > 0.05) → NU sunt semnificative statistic, adică valorile corespunzătoare factorilor Operator 1 și Operator 2 sunt aceleași statistic;

- linia Columns conține valorile asociate factorilor dependenți (m_x, m_y, m_z): SS_ Columns = 0,143; dof_ Columns = 2; MS_ Columns = SS_ Columns/dof_Columns = 0,143/2 = 0,0072; F_Columns = MS_Columns /MS_Width = 0,0715/0,3218 = 0,222; F_ Columns < Fcrit_ Columns (0,222 < 3,885); p-value_Sample > α (0,804 > 0.05) → NU sunt semnificative statistic, adică valorile corespunzătoare factorilor dependenți m_x, m_y, m_z sunt aceleași satatistic;

- linia Interaction conține conține valorile asociate interdependențelor factorilor independenți ( Operator 1, Operator 2) de factorii dependenți (m_x, m_y, m_z): SS_Interaction = 3,361, dof_Interaction = 2 și MS_Interaction = SS_Interaction/dof_Interaction = 3,3612/2 = 1,681, F_Interaction = MS_ Interaction/MS_Width = 1,681/0,322 = 5,223; F_ Columns > Fcrit_ Columns (5,223 > 3,885); p-value_Sample < α (0,023 < 0,05) → sunt semnificative statistic, adică există interdependențe ale factorilor dependenți (m_x, m_y, m_z) de cei independenți ( Operator 1, Operator 2);

- linia Within conține valori asociate interiorului variabilelor (Within): SS_Within = 3.8610, dof_Within = 12 și MS_Wihin = SS_Within/ dof_W = 3.8610/12 = 0,3218, asociate interiorului variabilelor;

- linia Total conține valorile asociate tuturor valorilor variabilelor; SS_Total = 7,450; dof_Total = 17.

Analiza dispersiilor bazat pe testul ANOVA cu doi factori cu replicație are ca scop evidențierea dispersiilor induse de cei doi factori, de interacțiunile dintre aceștia și de cele inexplicabile.

Ipotezele testelor ANOVA cu doi factori cu interacțiune:

- ipoteza de nul (H₀₁) pentru factorii Operator 1, Operator este admisă nefiind semnificativă (mediile liniilor nu diferă semnificativ) și ipoteza alternativă (H₁₁) pentru factorii Operator 1, Operator 2, ESTE semnificativă (mediile liniilor diferă semnificativ);

- ipoteza de nul (H₀₂) pentru factorii m_x, m_y, m_z este admisă nefiind semnificativă (mediile coloanelor nu diferă semnificativ) și ipoteza alternativă (H₁₂) pentru factorii m_x, m_y, m_z, ESTE semnificativă (mediile coloanelor diferă semnificativ);

- ipoteza de nul (H₀₃) pentru interacțiunea factorilor Operator 1, Operator 2 și m_x, m_y, m_z este respinsă fiind semnificativă (factorii m_x, m_y, m_z nu se modifică funcție de factorii Operator 1, Operator 2) și este admisă ipoteza alternativă (H₁₃) pentru interacțiunea factorilor Operator 1, Operator 2 și m_x, m_y, m_z, fiind nesemnificativă (factorii m_x, m_y, m_z se modifică funcție de factorii Operator 1, Operator 2).

Obs. Numerele măsurătorilor asociate variabilelor aleatoare dependente, corespunzător factorilor independenți, trebuie să fie egale

Fig. 2.63 Tabel cu valori ale datelor, indicatorilor și parametrilor statistici

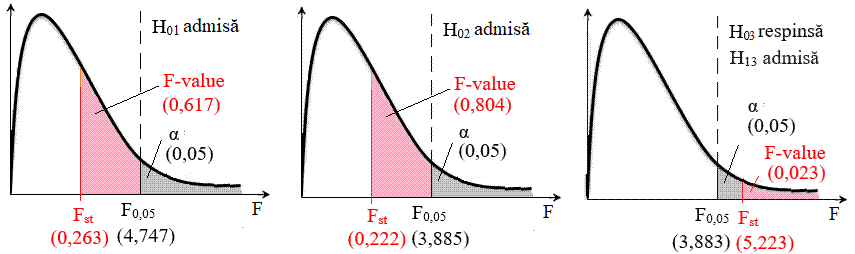
a b c

Fig. 2.64 Scheme asociate ANOVA: a – varianta H₀₁ admisă; b – varianta H₀₂ admisă; b – varianta H₀₃ respinsă

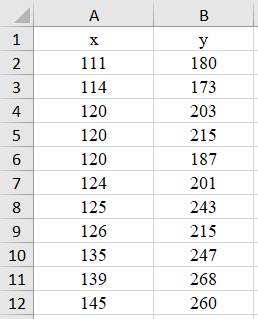
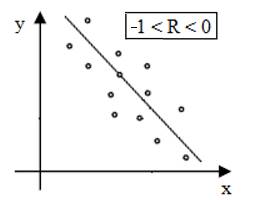
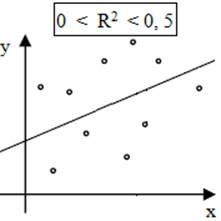
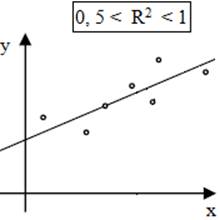
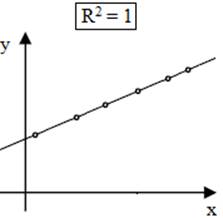
2.5.5.7 Analize inferențiale de corelare și regresie

2.5.5.7.1 Aplicație de analiza corelației a două variabile

Ap.2.20 Să se analizeze posibilitatea estimării prin regresie liniară a legăturii dintre variabilele x = {x₁, x₂, x₃ … x₁₁} și y = {y₁, y₂, y₃ … y₁₁} (coloanele A, B din fig.2.64,a). Se consideră că variabilele au repartiții normale (Ghid.Ap.2.20).

Descrierea problemei statistice de corelare:

- există două variabile la nivel de eșantion (număr redus de valori);

- analizele statistice descriptive univariate evidențiază parametrii statistici principali (ex: m_x, m_y, s_x, s_y) și normalitatea repartiției statistice;

- pornind de la ipoteza că o anumită valoare a variabilei independente x_i, mărime măsurată, y_i se supune unei distribuţii normale în jurul valorilor teoretice (estimate) y corespunzătoare celor independente x.

Rezolvarea problemei

Semnificații

Graficul Scatter-Plot (xy) care evidențiază norul de puncte și dreapta de regresie potențială (fig. 2.64,b) se folosește pentru a evalua, vizual și/sau analitic, corelaţia celor două variabile; astfel, se poate stabili posibilitatea existenţei unei dependenţe liniare între variabilele dependentă, y, şi independentă, x. Dreapta (linia) de regresie care aproximează (estimează) norul de puncte se definește cu relația, y = a + b x, în care a este ordonata în origine (valoarea variabilei y pentru variabila x = 0) și b = tgα este panta (α reprezintă unghiul dintre dreaptă și axa Ox). Pe de altă parte, această dreaptă se poate descrie similar în parametri Excel, Intercept = a, Slope = b. Astfel, în funcție de valoarea pozitivă/negativă a pantei Slope (b) se pot identifica drepte de regresie crescătoare/descrescătoare (fig.2.65,a/fig.2.65,b) Obs. Coeficienții Intercept și Slope se pot determina și cu funcțiie statistice Excel, INTERCEPT și, respectiv, SLOPE

Interpretări

Pentru a se se evidenția posibilitatea de prelucrare prin regresie liniară se impune un studiu preliminar a norului de puncte, de obicei, prin analiza coeficientului de corelație (Pearson), R ϵ [-1, 1] ca măsură a asocierii celor două variabile, pentru a se modela prin regresie liniară. Valorile pozitive/negative ale acestui coeficient de indică o corelaţie directă între variabilele y şi x care poate fi pozitivă/negativă (fig.2.66,b,c,d/fig.2.66,a). Cu cât valorile sunt mai apropiate de 1, respectiv, -1, cu atât legătura dintre cele două variabile este mai puternică, respectiv, mai slabă. Deoarece, R tinde să supraestimeze asocierea dintre y şi x, în practică, se preferă, coeficientul (gradul) de determinare, R^2ϵ [0, 1], pătratul coeficientului de corelaţie (R-square), care exprimă “tăria” asocierii (potrivirii) celor două variabile. În cazul, R^2 = 1, se evidențiază corespondenţa deplină (potrivire perfectă) a variabilei dependente y de variabila independentă x, toate punctele sunt pe dreapta de regresie (fig. 2.66,d), iar pentru, R^2 = 0, teoretic, nu există nicio dependență liniară între variabile (nefiind exclusă o dependenţă neliniară: exponențială, polinomială cu grad mai mare ca unu etc.). Pentru valori R^2 < 0,5 se poate aprecia că aproximativ mai puțin de 50% din valorile variabilei y sunt corelate cu ale variabilei x (fig. 2.66,b) spre deosebire de cazurile cu R^2 > 0,5 în care mai mult de 50% sunt corelate (fig. 2.66,c); cu cât R^2 se apropie de 1 ca atît punctele sunt mai apropiate de dreapta de regresie, de-o parte si de alta (model perecis). Coeficientul de determinare, R^2 ca măsură a concentrării (ajustării, potrivirii) punctelor experimentale în jurul dreptei de regresie exprimă cantitativ (procentual) o valoare care arată cât din dispersia (varianța) variabilei dependente se regăsește (influențează) în variabila independentă. De ex. R^2 = 0,8357 (fig. 2.64,b), arată că 83,57% din dispersia variabilei independente x influențează variații ale variabilei dependente y. Obs. În practică se pot folosi următoarele aprecieri ale corelației variabilelor x şi y: R^2 = 0…0,2 reprezintă o foarte slabă (improbabilă); R^2 = 0,2…0,4 – slabă; R^2 = 0,4…0,6 – rezonabilă; R^2 = 0,6…0,8 – de intensitate medie; R^2 = 0,8…0,95 – puternică (înaltă); R^2 = 0,95…1 – foarte puternică. În fig.2.64,a se prezintă graficul Scatter asociat variabilelor x și y (fig.2.64,a) în care se observă că alături de dreapta de regresie potențială apar: relaţia de definire, y = 2,8645 x - 141,65 , în care, 2,864 reprezintă panta dreptei (slope) şi ordonata în origine, - 141,655; coeficientul de determinare R^2 = 0,8357 evidenţiază o legătură puternică (83,57 %) a variaţiilor variabilei dependente y de ale variabilei independentă x

a	b
Fig. 2.64 Valori ale datelor și graficul de regresie: a – tabel cu valori ale variabilelor; a – dreapta de regresie potențială (tendință)

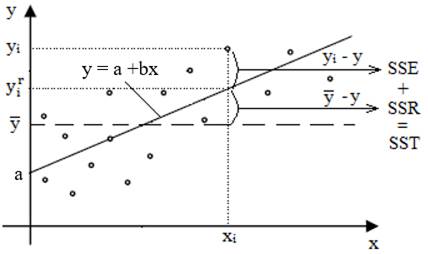
a b

Fig. 2.65 Drepte de regresie: a – crescătoare; b – descrescătoare

a	b
c	d
Fig. 2.66 Tipuri de corelații: a – negativă; b, c, d – pozitive

2.5.5.7.2 Aplicație de analiza regresiei liniare simplă

Ap.2.21 Să se analizeze posibilitatea estimării prin regresie liniară a legăturii dintre variabilele x = {x₁, x₂, x₃ … x₁₁} și y = {y₁, y₂, y₃ … y₁₁} (coloanele A, B din fig.2.71,a). Se consideră că variabilele au repartiții normale (Ghid.Ap.2.21).

Descrierea problemei statistice:

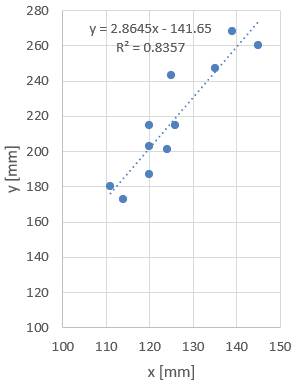
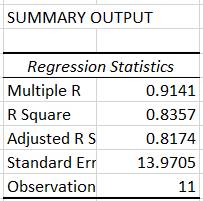
- există două variabile la nivel de eșantion: dependentă (y) care trebuie estimată (prezisă) în funcție de variabila independentă (x); eșantioanele (variabila dependentă, variabila independentă) sunt integrabile în populații;

- analizele statistice descriptive univariate evidențiază parametrii statistici principali (ex: m_x, m_y, s_x, s_y) și normalitatea repartiției (statistice);

- analiza de corelație indică o valoare a coeficeintului de determinare (R² = 0,8357; fig. 2.64,b; v. Ap.2.20) căreia îi corespunde acceptabilitatea unei regresii liniare;

- se identifică variabila dependentă ca predictor (estimată) și variabila dependentă numită și criteriu;

- se pornește de la ipoteza că valorile variabilelor (independentă și depenedentă) au distribuţii normale;

- analiza regresie va indica cât de bine măsurătorile asociate variabilei independente estimează/prezic valorile variabilei dependente.

Rezolvarea problemei

Semnificații

Pentru studiul statistic modelul de regresie Excel are la bază modulul ANOVA prin care se arată existența/inexistența de diferențe semnificative din punct de vedere statistic între valorile a două sau mai multe seturi de date independente (inversul corelației); parametri ANOVA indică că modelul este relevant adică parametrii relației de regresie diferă semnificativ de zero; prin această metodă statistică se poate verifica dacă modelul de regresie folosit este bun și în sensul estimării cât mai corecte a valorilor variabilei dependente. Acurateţea valorii estimate arată cât de bine se potriveşte dreapta de regresie cu valorile măsurate (xi,yi). Estimarea variabilei dependente se face prin intermediul coeficienților dreptei de regresie; testele efectuate precum și satabilirea intervalelor de încredere au la bază pragul de semnificație α = 0,05 (5%)

Interpretări

Tabelul SUMMARY OUTPUT conține date statistice (fig. 2.67,a): Multiple R = = = 0,914, coeficientul de corelație multiplă (mai multe variabile independente); în acest caz există o singură variabilă independentă; acest coeficient arată cât din dispersia variabilei dependente afectează dispersia variabilei independente. R Square = 0,8357 reprezintă coeficientul de determinare (R^2 = 0,8357; fig. 2.64,b; v. Ap.2.20). Ajusted R Square = 0,8174, coeficientul de determinare corectat (ajustat) este introdus pentru a contracara parțial, efectul creșterii, unori nejustificat, a lui R^2 (R Square) care apare în cazul numărului variabilelor independente mărit (pentru regresii multiple); acesta se determină ținând cont de numărul de predictori (variabile independente) integrați în modelul de regresie; valori mari ≈ 0,9 indică nivel ridicat de estimare. Standard Error = 13,9705, eroarea standard a estimaţiei (a nu se confuda cu indicatorul descriptiv eroarea standard, (v.subcap.2.5.3.5), măsoară dispersia variabilelor dependente estimate în jurul mediei; reprezintă media distanțelor punctelor din afara liniei de regresie la punctele estimate pe linia de regresie (media distanțelor SSE, din fig. 2.68); astfel cu cât punctele norului sunt mai aproape de linia de regresie cu atât valorea estimației erorii standard este mai mică. Obs. O valoare mare a erorii standard a estimației arată că punctele (obținute în urma măsurătorilor) sunt la distanță mare față de dreapta de regresie și deci, aceasta este mai puțin reprezentativă pentru datele reale și valorile prognozate sunt afectate de erori mari; valori mici ale erorii standard arată că modelul de regresie este precis. Observations = 11, numărul de valori (măsurători) ale variabilelor este egal cu numărul de puncte ale norului. Primul tabel ANOVA (fig.2.67,b) conține date statistice care evidențiază (demonstrează) statistic existența regresiei între cele două variabile: Coloana df reprezintă gradele de libertate egale cu numărul variabilelor independente mai puțin numărul de restricții la care sunt supuse: df_Regression = k = 1, numărul variabilelor independente ale regresiei (k >1, regresia liniară multiplă); df_Residual = n - k – 1 = 9, gradele de libertate pentru studiul erorilor (Residual) unde, n = 11, reprezintă numărul valorilor variabilei independente; df_Total = n – 1, gradele de libertate totale pentru studiul variabilității. Coloana SS (Sum of Square), suma pătratelor abaterilor valorilor regresiei: Linia Regression, SSR (Sum of Square Regression), suma pătratelor abaterilor valorilor estimate faţă de media (fig. 2.68), SSR = = 8932,1560; valoarea SSR evidențiază sintetic diferența dintre modelul de regresie (liniar) raportat la modelul de medie (constant, linia din fig.2.68. Linia Residual, SSE (Sum of Square Error), suma pătratelor abaterilor (reziduurilor, erorilor) valorilor măsurate în jurul dreptei de regresie; calitativ reprezintă dispersia (variația) din variabila dependentă care este inclusă în modelul de regresie; cantitativ este suma pătratelor distanțelor punctelor din afara liniei de regresie la punctele estimate de pe linia de regresie, SSE = = 1756,5712 (fig. 2.68); în general, cu cât valoarea SSE este mai mică cu atât modelul de regresie descrie mai bine dispersia norului de puncte. Linia Total, SST (Sum of Square Total), suma totală a pătratelor abaterilor (erorilor) de măsurare, SST = = SSE + SSR = 10688,7273. Obs. - Variaţia valorilor variabilelor în jurul valorii medii (SST) se descompune în doi termeni: primul (SSR) exprimă variaţia valorilor estimate în jurul mediei şi al doilea (SSE) generat de reziduurile ajustării (fig. 2.68). Prin urmare, regresia estimată va fi cu atât mai bună cu cât ultimul termen va fi mai mic, sau cu cât variaţia valorilor estimate va fi mai apropiată de variaţia valorilor observate. - Valoarea coeficientul de corelaţie se poate determina și cu relația, Multiple R = SSR/SST = 8962,1560. 10688.7273 = 0,9143. Coloana MS reprezintă media sumelor pătratelor abaterior valorilor (Means of Sum of Square), MS = SS/df: MS_Regresion = SSR/df_Regresion = 8932,1560/1 = 8932,1560, MS_Residual = SSE/df_Residual = 1756,5712/9 = 195,1746. Coloana F, indică valoarea funcției statistice FISCHER pentru testul-F, folosit pentru verificarea existenței regresiei liniare cu ipoteza de nul H0, b = 0 (nu există o relație liniară între variabila independentă și cea dependentă) și ipoteza alternativă H1, b ≠ 0. F = MS_Regresion/MS_Residual = 8932,1560/195,1746 = 45,7560; testul F se aplică pentru procesul de regresie în ansamblu. Coloana Significance F, prezintă semnificația statistică F-value (P-value) care se determină cu funcția Excel FINV în funcție de valoarea F; Significance F = 0,0001. Concluzie (decizie) test F (fig. 2.69): deoarece F-value < α (0.0001 < 0.05) testul este semnificativ, ipoteza nulă (H0) este respinsă și se acceptă ipoteza alternativă (H1) cu probabilitatea p = 0,05 (95%); astfel, b ≠ 0 și există o relație liniară (dreaptă de regresie) între variabila independentă și cea dependentă și, deci modelul de regresie este puternic semnificativ (relevant). Obs. În cazul acceptării ipotezei de nul, Significance F > α, se acceptă ipoteza de nul H0(b = 0) și nu există dreaptă de regresie (variabila dependentă y nu poate fi influențată de variabila independentă x) și nu poate identifica un model liniar valid (regresia liniară nu este adecvată pentru estimarea variabilei independente). Al doilea tabel ANOVA (fig.2.67,b) conține date statistice care evidențiază valorile parametrilor regresiei (v.fig.2.65) precum și încrederea statistică în parametrii obținuți: Linia Intercept, indică date despre ordonata în origine (a) a dreptei de regresie, Linia X variable 1, include date despr panta (b, Slope) a dreptei de regresie. Coloana Coefficients, arată valorile coeficienților dreptei de regresie: Intercept = -141,6546, X Variable 1 = 2,8645; valoarea coeficientului X Variable 1 arată cu cât crește (descrește, în cazul X Variable 1 < 0) variabila dependentă pentru creșterea cu o unitate a variabilei indepenedente; valorile coeficienților dreptei de regresie permit calculul valorilor estimate corespunzătoare valorilor variabilei independente x cu relația: Predicted y = Intercept + X Variable 1 * x (fig. 2.70). Coloana Standard Error, valorile erorilor standard asociate coeficienților dreptei de regresie: Standard Error_Intercept = 53,2504; Standard Error_X Variable 1 = 0,4234; aceste valori indică măsuri ale preciziilor coeficienților obținuți; valoarea mare a erorii standard asociată unui coeficient indică că acesta este imprecis (de ex. valoarea Error_Intercept = 53,2504 arată că coeficientul Intercept este cu imprecizie mărită față coeficientul X Variable 1 = 0,4234); un valoare a coeficientului mult mai mare decât eroarea sa standard implică probabilitatea mărită ca coeficientul să nu fie zero. Coloana t-Stat, reprezintă valorile funcției statistice t (STUDENT) și se determină cu relațiile: t-Stat_Intercept = Intercept/ Standard Error_Intercept = -141,6546/53,2504 = -2,6602; t-Stat_ X Variable 1 = X Variable 1/Standard Error_X Variable 1 = 2,8645/0,4234 = 6,7650; și aici se observă că cu valori ale coeficientului mai mari decât eroarea sa standard implică probabilitate mărită ca coeficientul să fie „departe” zero. Obs. Testul t (STUDENT) se aplică separat pentru fiecare coeficient al dreptei de regresie spre deosebire de testul F (FISHER) se aplică pentru procesul de regresie în ansamblu. Coloana p–value, arată semnificația statistică t-value (p-value): p-value_Intercept = 0,0260, p-value_ X Variable 1 = 0,0001; valoarea acestui parametru se compară cu α, pragul (nivelul) de semnificație); p-value < α arată că modelul de regresie utilizat aproximează bine datele, variabila independentă are influență cvasitotală asupra variabilei dependente; p-value > α, variabila independentă are influență parțială asupra variabilei dependente și pentru îmbunătățire se pot adăuga noi valori (măsurători). Concluzii (decizii) ale testelor t: Testul t pentru coeficientul Intercept (nivelul de semnificație, α = 0,05): ipoteza de nul H0, a = 0; ipoteza alternativă H1, a ≠ 0; decizie: deoarece p-value_Intercept < α (0,0260 < 0,05), testul este semnificativ, se respinge ipoteza de nul H0(a = 0), se acceptă ipoteza H1, a ≠ 0 și există (din perspectiva coeficientului Intercept) dreaptă de regresie cu probabilitatea p = 0,95 (95%). Testul t pentru coeficientul X Variable 1 (nivelul de semnificație, α = 0,05): ipoteza H0, b = 0; ipoteza alternativă H1, b ≠ 0; decizie: deoarece, p value_X Variable 1 < α (0,0001 < 0,05, testul este semnificativ, se respinge ipoteza de nul H0(b = 0), se acceptă ipoteza H1, b ≠ 0 și există (din perspectiva coeficientului X Variable 1) dreaptă de regresie cu probabilitatea p = 0,95 (95%). Coloana Lower 95%, indică limita inferioară a intervalului de încredere: Lower 95%_Intercept = -262,1154, Lower 95%_ X Variable 1 = 1,9067. Coloana Upper 95%, indică limita superioară a intervalului de încredere: Upper 95%_Intercept = -21,1938, Uppr 95%_X Variable 1 = 3,824. Deoarece, coeficienții Intercept şi X Variable 1 sunt semnificativi statistic (5%), aparțin intervalelor de încredere [Lower 95%, Upper 95%]: -141,6546 ϵ [- 262,1154, - 21,19838], 2,6845 ϵ [- 1,9067, - 3,8224]; intervalul de încredere arată că dreapta de regresie există cu siguranță (95%) în limitele acestui interval. Obs. În cazul în care acest interval cuprinde valoarea 0, ipotezei de nul, H0, este adevărată și se consideră că R (coeficientul de corelație) este semnificativ statistic; în cazul valorilor mici ale coeficientului de corelație este necesară testarea semnificației cu testul t (STUDENT). Tabelul RESIDUAL OUTOUT conține valori parametri statistici privind valoarea și precizia (eroarea) de estimare asociați valorilor variabilei dependente, coloana Observation, numărul valorii (măsurătorii) din setul de date prezise (fig. 2.71,a): Coloana Predicted Y, conține valorile variabilei dependente estimată (prezisă) de regresie cu relația Predicted y = Intercept + X Variable 1 * x, unde x sunt valorile variabilei dependente (coloana B din fig. 2.71,a); ex. pentru Observation 4, x = 120 și y = 215, valoarea, Predicted y = -141,6546 + 53,2504 * 120 =202,0902. Coloana Residuals, eroarea valorii prezisă (estimată); ex. pentru Observation 4, y = 215 (fig. 2.71,a), Predicted y = 202,0902 și Residuals = y – Predicted y = 215 - 202,0902 = 12,9098. În fig. 2.72 se prezintă graficul erorilor (Residuals Plot) în funcție de valorile variabilei independente (pe grafic se evidențiază 11 valori marcate cu romburi albastre); în acest grafic se evidențiază că erorile sunt împrăștiate în jurul axei “zero” sub formă de bandă uniformă (deci, regresia este “puternic“ liniară); în cazurile în care împrăștierea erorilor este după alte forme (bandă trapezoidală, circular etc.) se poate concluziona o liniaritate “slabă” (se poate încerca un model de regresie neliniar). În fig. 2.73 se prezintă graficul dreptei de regresie estimate generat în Excel. Obs. Corespunzător unei valori a variabilei dependente y apar două componente: valoarea obținută prin regresie (Predicted y) şi erorea (Residuals), inexplicabilă de modelul de regresie. Coloana Standard Residuals (fig. 2.71,b), eroarea (reziduul) standard, se determină ca raportul dintre Residuals și Abaterea standard (SD) a reziduurilor valorilor erorilor standard în raport cu media; acestea indică cum sunt împrăștiate erorile în raport cu media în unități de abateri standad (scorul z); valori în intervalul ±3 arată participarea valorilor la procesul de estimare prin regresie; valori în afara intrvalului ±3 indică că valorile variabilei dependente nu au efect în valorile estimate și sunt considerate aberante (pot fi excluse sau dacă sunt de interes se reface experimentul considerând valori suplimentare). Obs. Valorile erorilor standard ale reziduurilor se pot determina și cu funcția Excel STDEV. Tabelul PROBABILITY OUTPUT (fig.2.74), conține valori ale probabilității normale ale variabilei dependente corespunzătoare percentilelor asociate; aceste valori sunt folosite pentru evaluarea normalității distribuției valorilor acesteia. Graficul Normal Probability Plot din fig. 2.74,b indică aranjarea valorilor variabilei independente cvasiliniar ce conduce la ipoteza că valorile variabiei dependente sunt distribuite după o curbă normală (clopotul lui Gauss).

a

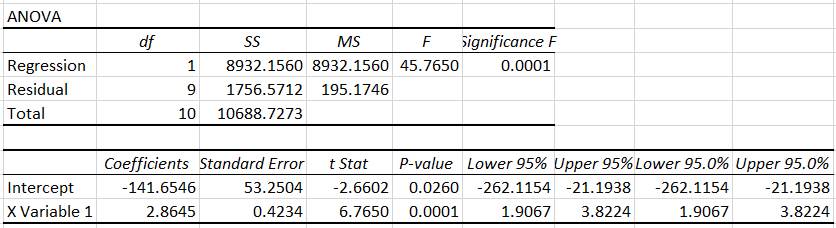
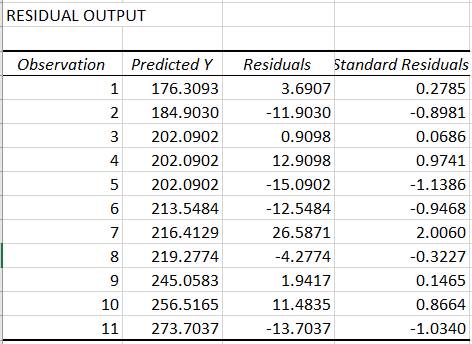
b

Fig. 2.67 Valori ale parametrilor statistici: a – tabel cu valori indicatori descriptivi; b – tabel cu valori parametri ANOVA

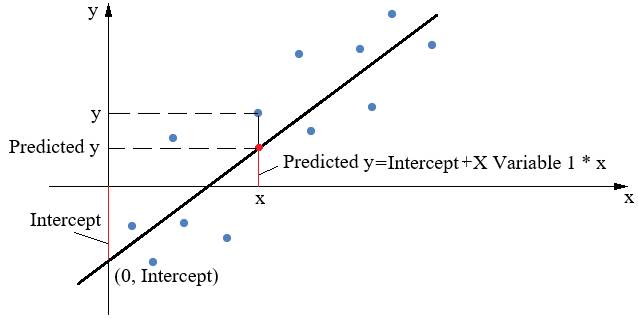
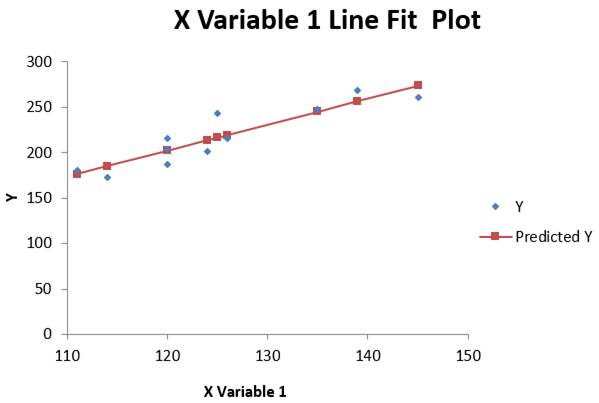
Fig. 2.68 Dreapta de regresie teoretică cu parametri caracteristici

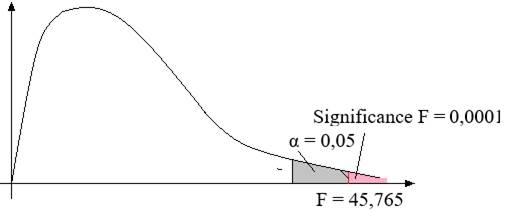
Fig. 2.69 Schema testului Fischer

Fig. 2.70 Dreapta de regresie estimată cu parametri caracteristici (Excel)

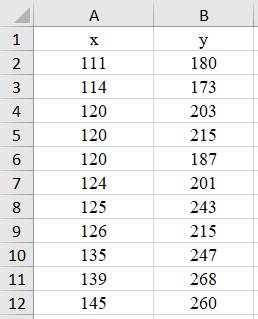
a b

Fig. 2.71 Valori seturi de date și parametri satistici de estimare: a – tabel cu valori variabile; b – tabel cu valori parametri de estimare

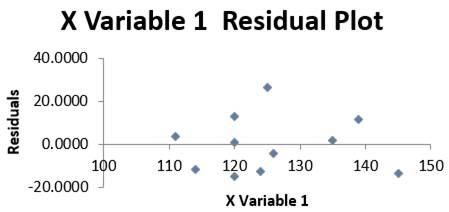
Fig. 2.72 Graficul erorilor asociate variabilei dependente

Fig. 2.73 Dreapta de regresie estimată

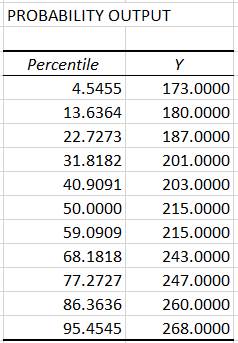
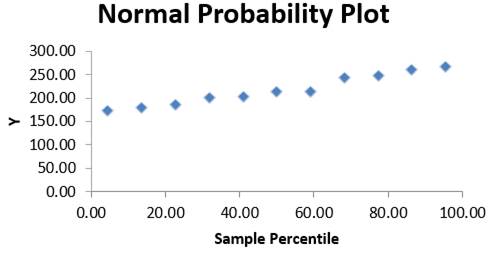
a b

Fig. 2.74 Valori și grafic de evidențiere a normalității variabilei dependente: a – valori ale probabilităților normale; b – graficul probabilităților normale

2.6 ETAPELE STUDIILOR (CERCETĂRILOR) EXPERIMENTALE PRIN MĂSURĂTORI

2.6.1 Aspecte generale

Cercetarea experimentală în inginerie este o metodă științifică care presupune un proces de generare și de testare (verificare) a unor ipoteze statistice cu scopul de a fundamenta prin legi un fenomen/proces fizic. Pentru aceasta bazat pe dovezi empirice, de obicei în inginerie exprimate printr-un număr redus de valori obținute prin măsurători, se pot lua decizii (concluzii) valabile pentru cazul general cu o infinitate de valori posibile. Cercetarea experimentală poate fi tratată ca un proces unifactorial, factorul (parametrul) studiat se modifică cu considerarea celorlați factori nemodificați (constanți) sau multifactorial, toți factorii în fiecare moment sunt luați în considerare. În practică, se întâlnesc, frecvent, cazuri în care se ia în considerare la măsurare un singur factor. Având în vedere că cercetările experimentale de laborator legate de organele de mașini, frecvent, sunt unifactoriale, considerând doar variabilitatea unui parametru în raport cu alți parametrii considerați invariabili (constanți), în continuare, se vor face referiri doar la acest tip de cercetări.

Validitatea unui cercetări experimnetale fiind dată de precizia de descriere a fenomenului fizic care se urmărește a fi studiat, răspunde la întrebarea: se măsoară cu adevărat ceea ce se intenționează să se măsoare ? Deoarece, în inginerie studiile experimentale se realizează pe eșantioane, în practică, apar amenințări legate de lipsa de reprezentativitate a acestora, care pot conduce la generalizări a rezultatelor neconcludente. Pe de altă parte, validitatea rezultatelor unei cercetări este determinată și de considerarea cu fidelitate a dependențelor de tip cauză-efect care influențează parametrul măsurat. Validitatea rezultatelor unei cerectări depinde în mare parte și de procesul de definire și planificare a etapelor cercetării. Definirea problemei care urmează a fi investigată presupune un studiu bibliografic în domeniu, din care să rezulte: ipoteze veridice, modelele robuste, instrumentele de măsurare adecvate, analiza şi interpretarea datelor riguroase, prezentarea rezultatelor etc.

2.6.2 Planificarea (proiectarea) experimentelor unifactoriale

2.6.2.1 Definirea și enunțul problemei

Proiectarea unui experiment deoarece presupune definirea cu acuratețe a relațiilor cauză-efect are implicații directe asupra validităţii rezultatelor.

Delimitarea domeniului de studiu (ce se cercetează?) presupune, preliminar, studiul biblografic de analiză a nivelul de cunoaștere a fenomenului de studiat, rezultate se urmăresc, posibilitățile de obținerie datelor (se recomandă să adoptarea unei variante mai prin care datele sunt achiziționate (colectate) cât mai rapid și cu costuri cât mai mici).

Cercetările experimentale în inginerie bazate pe măsurători, de obicei, sunt cercetări cantitative care bazat pe instrumente statistice stabilesc relații de cauzalitate și/sau testează teorii.

2.6.2.2 Scopul și obiectivele cercetării experimentale

Scopul unei cercetări reprezintă intenția generală (viziunea de ansamblu) și rezultatul principal pe care cercetătorul urmărește sale atingă.

Obiectivele unei cercetări științifice experimentele se pot referi la descrierea, modelarea și/sau predicția unui fenomen (proces) fizic urmărind:

- obţinerea de date, informaţii şi cunoştinţe noi, relevante pentru structura şi funcţionalitatea procesului/fenomenului;

- modelarea matematică analitică, empirică sau/şi numerică a dependenţelor care caracterizează procesul/fenomenul de investigat;

- simularea şi predicţia stărilor şi evoluţiei specifice.

Obiectivele cercetării experimentale conțin activitățile de realizat pentru a rezolva problema de cercetare și trebuie să fie în concordanță cu enunțul problemei atât la nivel general cât și la nivel specificitate. Obiectivul general al unei cercetări trebuie să includă scopul final al investigației pentru a dobândi noi cunoștințe folosind metode și tehnici specifice domeniului problemei. Obiectivele specifice indică etapele ce trebuie parcurse pentru atingerea obiectivului principal.

2.6.2.3 Stabilirea populației țintă (de interes) și a ipotezelor statistice

Populaţiile statistice asociate experimentelor cu măsurători se definesc prin totalitatea valorilor posibile ale mărimii măsurate având una sau mai multe caracteristici comune. De obicei, populațiile statistice asociate mărimii măsurate sunt ipotetice și infinite (există un număr foarte mare de valori posibile ale mărimii măsurate). Pentru cunoașterea caracteristicilor unei populații este necesar să se cunoască toate valorile posibile ale mărimii măsurate, fapt care deoarece pentru obținerea acestora ar fi necesare un număr foarte mare de experimente (desigur, în perioade de timp și cu costuri mult mărite), practic este imposibil. Astfel, se poate aprecia carcteristicile populației statistice numai pe baza unei mulțimi finite (eșantion, probă) de valori ale mărimi măsurate inclusă în mulțimea infinită a populației și cu proprietatea ca fiecare element din populație să aibă aceași probabbilitate de a face parte din eșantion. Deoarece, cercetarea bazată pe experimente cu măsurători, este o cercetare de eşantion, se pune problema generalizării observaţiilor obţinute pe un număr limitat de valori, la întreagul domeniu de valori posibile, obţinându-se astfel legi cu aplicare generală. Generalizarea este posibilă aplicând statistica matematică care oferă metode și tehnici științifice de analiză a variabilității valorilor măsurate la nivel de eșantion.

Ipotezele statistice au rolul de a descrie în termeni concreţi ce se aşteptă de la studiul urmărit, care, în inginerie, de obicei, este direcționat, pe de-o parte, spre testarea sau verificarea teoriei, și pe de altă parte, spre obținerea unor valori (constante) sau dependențe care ulterior stau la baza modelelor teoretico-experimentale. Ipotezele pot fi enunţuri despre posibile relaţii dintre mai multe variabile dintre care una este dependentă (cea de studiat). În practică, fiecărui fenomen (proces) de studiat i se asociază (cel puţin în mod explicit) un set restrâns de ipoteze. Pentru validitatea cercetării experimentale prin generalizare se va urmări ca în urma măsurătorilor și prelucrării statistice a datelor, nicio ipoteză să nu poată fi invalidată.

Modul clasic de testare al ipotezelor statisttice este bazat pe metoda ipotezei nule prin care dacă se demonstrează că între două variabile nu există nicio relație (se infirmară ipoteza nulă) cu un risc impus (de obicei, 5%) se poate concluziona (decide) că ipoteza contrară (alternativă) este validă, între cele două variabile există relație de dependență (de obicei, cu probabilitatea de 95%).

Este important să se formuleze ipoteze clare și distincte care să fie verificate înainte de a proceda la colectarea datelor.

2.6.2.4 Determinarea volumului (mărimii) eșantionului

Studiile experimentale, care implică măsuaraea tuturor valorilor parametrului (de obicei, infinite), sunt, de regulă, imposibil de realizat şi se impune constituirea unui eşantion (un set finit de măsurători) care se impune să fie reprezentativ, în raport cu mulţimea totală (populația), comparabil, în raport cu alte eşantioane similare, şi compatibil, în raport cu obiectivele studiului. Volumul necesar al eşantionului exprimat prin numărul valorilor măsuarte ale unui parametru are implicaţii asupra rezultatealor finale (concluzii, generalizări). Astfel, dacă volumul eşantionului este redus, rezultatele obţinute pot fi inprecise, uneori, chiar îndepărtate de cele reale, iar dacă eşantionul este numeros, rezultatatele pot fi precise, cvasiapropiate de cele reale. Altfel spus, eşantionul ca formă de bază a cercetării ştiinţifice bazată pe un număr redus valori obţinute prin măsurători repetate conduce, prin prelucrări statistice, la cunoaşterea populației (mulţimea totală) asociată parametrului măsurat. În practică, din considerente de costuri reduse, studiile statistice consideră eşantioane cu volume mult reduse decât volumul populației (foarte mare sau, deseori, infinit).

În literatura de specialitate se evidenţiază mai multe modele de determinare a numărului valorilor măsurate repetitiv (în aceleaşi condiţii). Pentru studiile experimentale în ingineria mecanică se poate folosi modele bazate pe puterea statistică care reprezintă probabilitatea de a obține rezultate semnificative statistic. La planificarea experimentului se impune determinarea volumului minim al eșantionului (numărul minim de măsurători) pentru a obține puterea statistică dorită (1- β), corespunzătoare valorilor unui nivel de semnificație (α) impus și a unui efect estimat (β). Mărimea efectului estimat se stabilește pe baza unor experimente similare, considerate teoretice, sau din documente din literatura de specialitate. Valoarea mărită a puterii statistice (de ex. 0,8) indică că volumul eșantionului conduce la rezultate relevante statistic cu un nivel de semnificație α (de ex. α =0,05) pentru a determina un efectul mai mic decât cel estimat (de ex. β = 0,2), iar dacă puterea statistică are valori reduse (de ex. mai mici ca 0,5) se poate considera că rezultatele nu sunt relevante statistic (valoarea efectului este mai mare decât cel estimat) și în consecință se impune repetarea experimentului pentru un eșantion cu volum mai mare, dacă este posibil practic. Modulul ANOVA din pachetul Microsoft Excel permite analize statistice pentru determinarea acestor parametri atât a priori cât și post-hoc. În ingineria mecanică, uzual, eșantioanele experimentelor cu măsurători au numărul de valori, n = 10…100, dependent de tipurile problemelor și metodelor de analiză statistică.

2.6.3 Realizarea experimentelor, colectarea şi/sau achiziţia datelor

Prin măsurare se atribuire valori numerice unei caracteristici a fenomenului fizic și se obțin valori ale unei variabile. Pentru aceasta este nevoie de un instrument (dispozitiv) de măsurare care să genereze valori numerice cu o unitate de măsură raportate la un punct de referință (zero).

Procesul de măsurare este influențat de factori perturbatori care, de obicei, au următoarele cauze: principiul sau metoda de masurare; mijloacele (instrumentele) de măsurare; caracteristicile mediului ambiant (temperatura, presiune, umiditate, vibrații etc.); obiectul supus masurării; operator etc. Astfel, valorile obținute prin măsurare sunt cu erori (v.subcap.2.3.2), dintre care cele aleatorii, de obicei, se iau în considerare pentru prelucrarea statistică. Aceste erori se obțin prin repetarea măsurătorilor (în condiții identice).

În procesul de pregătire a realizării măsurătorilor se vor analiza sursele de erori; se vor elimina, pe cât posibil, sursele erorilor sistematice şi se vor face evaluări ale erorii aleatorii maximale a rezultatelor pe baza erorilor maximale ale datelor iniţiale. Astfel, se vor analiza influenţele asupra măsurătorilor a diferiţilor factori exteriori (temperatură, presiune, umiditate), iar dacă aceastea sunt semnificative, se va proceda la eliminarea acestora sau la luarea în considerare la prelucrarea datelor şi la determinarea erorilor.

2.6.3.1 Colectarea datelor prin chestionare (online)

În inginerie, pentru variabile calitative, care nu se pot cuantifica numeric, se pot utiliza chestionare dedicate care pot fi accsate online.

Ap.2.22 Să se studieze statistic efectele introducerii la nivelul posturilor de conducere a autoturismelor a unui dispozitiv ADAS (Advanced Driver Assistance Sistem). Deoarece, parametrii de apreciere (confortul și siguranța) sunt calitativi și pentru aceștia nu se pot obține valori prin măsurare, se poate recurge la aprecieri subiective multiple care procesate statistic, deseori, pot da informații cvasifidele despre parametrii analizați. Pentru rezolvarea acestei probleme se propune folosirea aplicației Google Forms (Formulare Google) care prin integrarea în chestionare a răspunsurilor cu aprecieri posibile multiple (Linear Scale), conduce ușor la rezultate fezabile (Ghid.Ap.2.22).

2.6.3.2 Achiziţia automată a datelor

Sistemele de achiziție a datelor permit conectarea unui număr variabil de traductoare și senzori la o unitate centrală de procesare (calculator) pentru obținere de date numerice pentru prelucrări ulterioare (fig. 2.75).

Traductoarele au funcţia principală de transformare a unei mărimi neelectrice într-o mărime electrică. Senzorii pe lângă funcţia principală de transformare a unei mărimi neelectrice într-o mărime electrică, şi alte funcţii de prelucrare locală a datelor şi transmitere a lor sub formă de semnale numerice sistemul de achiziție a datelor sau direct la calculator. Creșterea gradului de inteligență a senzorilor, în ultimul timp, a condus la simplificarea sau chiar dispariția sistemelor de achiziție a datelor, fiind astfel legate hard sau chiar wireless la calculator. Sistemele de achiziție a datelor sunt structuri, cu precădăre, electronice care condiționează, amplifică, convertesc digitizează, semnale electrice.

Conectarea la calculator a sistemelor de achiziție, de obicei, se face pein interfețe standard de comunicare serială (RS-232, I²C) sau paralelă (IEEE 488). Pentru preluarea și prelucrarea semnalelor direct de la sezori sau prin intermediul sistemelor de achiziție de date, calculatoarele sunt echipate cu plăci de achiziție. Sistemele și plăcile de achiziție de sunt asociate cu pachete software specifice (proprii) sau specializate (LabView, MatLab)

Fig. 2.75 Structura generală a unui sistem de achiziție automată a datelor

2.6.4 Prelucrarea statistică şi analiza datelor

Procesul de măsurare este influențat de factori perturbatori care, de obicei, au următoarele cauze legate de: principiul sau metoda de masurare; mijloacele de masurare; caracteristicile mediul ambiant (temperatura, presiune, umiditate, vibratii etc. ); obiectul/procesul/fenomenul supus masurării; operator etc. Astfel, valorile obținute prin măsurare sunt cu erori (v. subcap. 2.3.2), dintre care cele aleatorii se iau în considerare pentru prelucrarea statistică.

Prin repetarea măsurătorilor (în condiții identice) valorile mărimii obținute x_i și implicit valorile erorilor (abaterilor), z_i = x_i – m, raportate la valoarea adevărată m (media), pentru cazurile experimentelor valide, respectă următoarele poprietăți: valori mici ale abaterilor (erorilor) z_i sunt mai frecvente decât valori mai mari; suma algebrică a erorilor z_i este nulă; distribuția probabilităților de apariție a erorilor z_i, p(z) să fie cât mai apropiată de cea normală (clopotul lui Gauss).

Populația statistică se acociază unui număr N mult mărit (tinde la ∞) al valorilor mărimii parametrului măsurat care verifică generalitatea (veridicitatea) modelului teoretic spre deosebire de eșantion care printr-un număr n redus de valori (de obicei, n ≤ 100) estimează mărimea adevărată asociată populației. De obicei, valorile variabilelor asociate mărimilor măsurate sunt evaluate prin intermediul unor parametri statistici de centrare (grupare, localizare): µ (media), pentru populație; m (media), pentru eșantion sau de împrăștiere (dispersie): σ², pentru populație; s², pentru eșantion.

Obs. De obicei, valorile µ = și σ² = /N, (deviație standard populație), pentru populații (cu N foarte mare), sunt constante (de referință); m = și s² = /(n-1) (deviație standard eșantion), pentru eșantioane (cu n redus) sunt variabile (de estimare, prognoză).

Datele numerice procesate de cercetător pot fi, cel mai adesea, rezultatele unor experimente proprii (măsurate într-o instalaţie de laborator) sau pot fi  preluate (adoptate) din literatura de specialitate (periodice, enciclopedii, baze de date etc).

După colectarea/achiziţia datelor experimentale, prima activitate ce trebuie desfăşurată este prelucrarea şi analiza primară, care presupune aplicarea unor metode probabilistice şi/sau statistice cu scopul verificării consistenţei, corelărilor, precum şi eliminării eventualelor valori eronate (grosolane, accidentale, sistematice). Ca urmare, uneori, analiza primară poate impune chiar necesitatea unor determinari experimentale suplimentare (repetate sau extinse), după care intreaga procedură se reia pentru noul set de date.

2.6.4.1 Analiza primară a datelor

Una din primele etape la analiza primară presupune identificarea valorilor afectate de erori aberante (grosolane) care, de obicei, sunt valorile minime sau maxime ale şirului de valori obținute experimental. Deoarece, aceste valori afectează negativ analizele statistice se impune eliminarea acestora. Dintre mai multe tehnici de identificare a valorilor aberante posibile, cea bazată pe graficul boxplot are un suport ststistic relevant (v.subcap.2.5.4.2).

Determinarea frecvenţelor valorilor unui set de date obținute prin măsurare, reprezentate tabelar, în vederea analizei frecvențelor (v.subcap.2.4.5.1) presupune parcurgerea următoarelor etape:

- organizarea valorilor într-un șir ordonat (coloană sau linie) crescător/descrescător (considerând, valori distincte);

- gruparea valorilor în subintervale (grupe, clase) cvasiegale, de obicei, prin divizarea dimensiunii intervalului, Amp = Max-Min, la numărul de de subintervale, adoptat apriori (adesea numărul claselor, cu precădere, în funcție de volumul eșantionului, este 5…15);

- identificarea numărul de apariții (frecvențe absolute) a fiecărei valori a setului de date în subdomeniile stabilite și generarea unui șir (linie sau coloană) al frecvențelor asociat șirului subdomeniilor.

- se calculează frecvențele relative (numărul de valori din fiecare clasă raportat la numărul total de valori) și sintetizarea tabelar a datelor despre subdomenii, frecvențe absolute și relative

După construirea tabelului frecvențelor, în general, analiza se continuă cu reprezentarea grafică sub formă de poligoane și/sau histograme (v.subcap.2.4.5.1). Poligoanele frecvenţelor se obţin prin reprezentarea de puncte în dreptul mijlocului fiecărei clase şi unirea acestor puncte prin linii drepte. În plus, la extremităţi, primul, respectiv ultimul punct corespunde valorii minime, respectiv maxime din şirul de date. Poligoanele de frecvenţă se utilizează, mai ales, în cazul când se doreşte compararea a două distribuţii reprezentate suprapus în acealași grafic.

Având în vedere că analizele statisice sunt aplicabile variabilelor aleatorii se impune și veificarea caracterului aleatoriu al datelor (x₁, x₂… x_n) care pentru a fi realizat cu probabilitatea α (coeficientul de încredere) implică respectarea inegalităților (testul Young),

VCI < M < VCS,

în care, M = cu = , VCI (Valoarea Critică Inferioară) și VCS (Valoarea Critică Superioară), se determină cu relațiile:

VCI = 0,491 + 0,081n - , VCS = 3,317 – 1,057 , pentru α = 0,95.

De asemenea, în practica analizelor statistice, în majoritatea cazurilor, se impune veificarea normalității distribuției (repartiției) valorilor datelor care de obicei, se poate face vizual, prin analiza graficelor frecvențelor (prin puncte, histogramă , boxplot etc.) (v.subcap.2.4.5.1), (v. subcap.2.3.2). Dacă graficul obținut are aspect de clopot (simetric cu un singur vârf), rezultatele măsurarilor se supun unei repartiții Gauss.

Normalitatea repartiției datelor experimentale se poate aprecia prin evaluarea apropiereii calitativ și/sau cantitativ de repartiţia normală prin:

- compararea graficelor: funcţia de repartiţie a datelor reale trebuie să fie cât mai apropiată de funcţia de repartiţie normală;

- compararea abaterii standard a datelor reale cu abaterea standard a repartiţiei normale care are valoarea, 1;

- analiza mărimii intervalului de împrăştiere a datelor în jurul mediei; cu cât acest interval este mai mic cu atât datele sunt mai grupate în jurul mediei.

- analiza coeficientul de formă care exprimă boltirea (ascuţirea) curbei de repartiţie (v.subcap.2.5.3.4); de obicei, pentru o formă specifică clopotului Gauss acesta are valori apropiate de 3; dacă acest coeficient este mai mare decât 3 atunci curba este mai ascuţită şi datele sunt concentrate în jurul valorii medii spre deosebire de cazurile cu valori mai mici ca 3 care conduc la curbe boltite și datele mai împrăștiate în juril mediei;

- analiza coeficientul de asimetrie care exprimă simetria curbei de repartiţie (v.subcap.2.5.3.4); valorile care indică apropiere acceptabilă de repartiția normală sunt în jurul lui 0; dacă acest coeficient este diferit de zero, curba este asimetrică, deplasată spre stânga sau spre dreapta, faţă de curba de repartiţie normală.

2.6.4.2 Prelucrarea statistică și analiza finală

Prelucrarea statistică a datelor experimentale (provenite din măsurători), în general, presupune următoarele etape:

- determinarea indicatori statistici (v.subcap.2.5.3.1);

- analize descriptive (v.subcap.2.5.4) și/sau inferențiale (v.subcap. 2.5.5.6);

- estimarea parametrilor populaţiei,

- determinarea erorilor de măsurare,

- stabilirea preciziei de măsurare etc.

Alegerea analizei descriptive și/sau a testului statistic depinde de natura datelor și de întrebarea de cercetare care este investigată. Rezultatele analizei statistice inferențiale vor furniza informații cu privire la faptul că ipoteza nulă poate fi respinsă în favoarea ipotezei alternative (care răspunde la întrebarea de cercetare).

În cazul măsurărilor indirecte se impune estimarea erorii aleatoare. De exemplu, pentru mărimea necunoscută, y = f(a, b, c …) cu a, b, c … valori măsurate direct, are valoarea medie, m_y = f (m_a, m_b, m_c …) și abaterea medie pătratică,

s_y = .

2.6.5 Interpretarea rezultatelor şi elaborarea concluziilor

Spre deosebire de legile fizice deterministe care guvernează cunoașterea unui fenomen/proces având la bază valori cunoscute ale unor mărimi la momentul inițial, legile statistice permit cunoașterea derulării viitoare a fenomenelor/proceselor doar în termeni probabilistici (probabilități, valori medii, erori statistice etc.).

Scopul interpretării rezultatelor unei cercetări statistice este de sintetiza concluzii cu referire la fenomenele/procesele studiate pentru a putea fi integrate la nivel de teorii sau date reprezentative. Procesul de interpretare a datelor care constă în stabili sensuri/fundamentări în contexte teoretice generale este diferit de cel de analiză a datelor care se face în raport cu obiectivele cercetării. O interpretare riguroasă a rezultatelor cercetării garantează faptul că acestea sunt legitime și de încredere și că contribuie la dezvoltarea cunoașterii în domeniul de studiu precizând limitele și implicațiile potențiale.

În subcap. 2.5.4 și 2.5.5. sunt prezentate aplicații de prelucrarea statistică a datelor, cu precădere obținute prin măsurări fizice, în care sunt evidențiate și aspecte de interpretarea rezultatelor