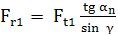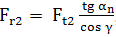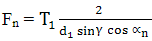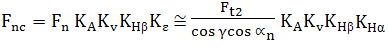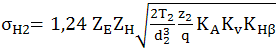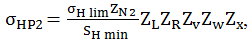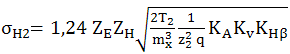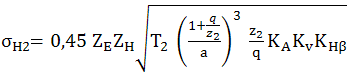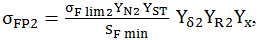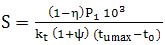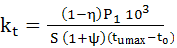AEV. ANGRENAJE EVOLVENTICE
AEV-T. STRUCTURA, CONSTRUCŢIA ŞI MODELAREA ANGRENAJELOR EVOLVENTICE
AEV-T.2 MODELAREA ANGRENAJELOR EVOLVENTICE
AEV-T.2.4 MODELAREA ANGRENAJELOR MELCATE CILINDRICE
|
CUPRINS |
|
AEV-T.2.4.1 PARTICULARITĂŢI GEOMETRICE ŞI FUNCŢIONALE ALE ANGRENAJELOR MELCATE CILINDRICE AEV-T.2.4.2 MODELAREA ÎNCĂRCĂRILOR AEV-T.2.4.3 MODEL DE CALCUL AL TENSIUNII DE CONTACT AEV-T.2.4.4 MODEL DE CALCUL AL TENSIUNILOR DE ÎNCOVOIERE AEV-T.2.4.5 MODEL DE CALCUL TERMIC |
|
Particularităţi geometrice şi constructive |
Parametrii cinematici şi geometrici principali |
|
-
Din
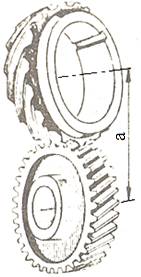
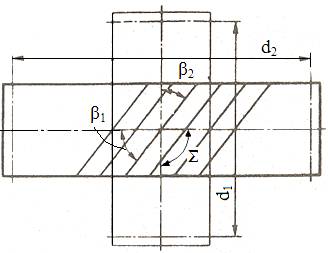
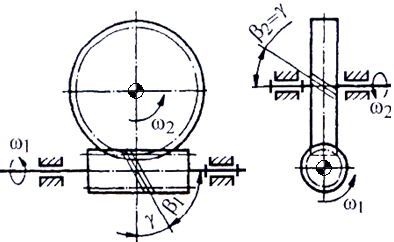
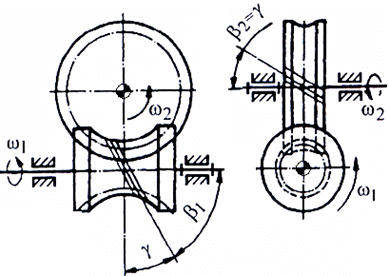
punct de vedere al poziţiei spaţiale a axelor, angrenajul melcat
este un angrenaj elicoidal (fig. AEV-T.2.4.1.1,
fig. AEV-T.2.4.1.3,a),
care are distanţa dintre axe
a şi
unghiul dintre acestea Σ = β1+
β2
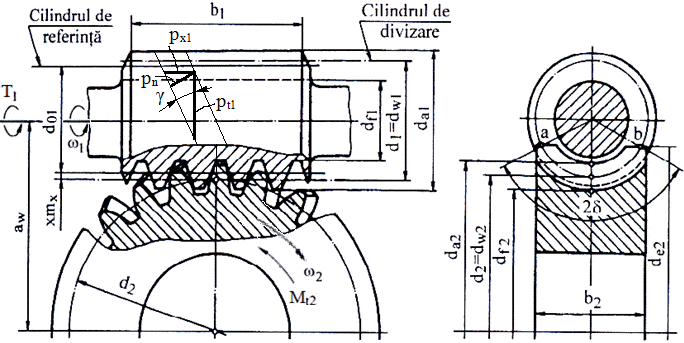
= 90o. - Angrenajul melcat cilindric are roata 1 (fig. AEV-T.2.4.1.2,a; fig. AEV-T.2.4.1.3,b) numită, melc, cu număr mic de dinţi (începuturi, z1 = 1…4) şi unghi mare de înclinare a danturii β1 = 90o – γ, iar roata conjugată, numită roată melcată, este o roată dinţată toroidală care îmbracă melcul cu unghiul de înclinare β2 = γ. - Angrenajul melcat globoidal, în plus de angrenajul melcat cilindric, are melcul cu forma globoidală (îmbracă roata melcată, fig. AEV-T.2.4.1.3, a; fig. AEV-T.2.4.1.3, c) - Datorită formei toroidale a roţii melcate danturile roţilor angrenajului melcat nu mai pot fi determnate de o cremalieră de referinţă ci de un melc de referinţă standardizat; sunt standardizate, în funcţie de procedeul de prelucrare, şase tipuri de melci de referinţă, dintre care cel mai utilizat este melcul arhimedic care, în secţiune axială, are flancul dintelui rectiliniu (fig. AEV-T.2.4.1.2,a). - Parametrii definitorii ai melcilor de referinţă standardizaţi sunt stabiliţi faţă de cilindrul de referinţă pe care grosimile plinuririlor dinţilor sunt egale cu cele ale golurilor dintre dinţi (fig. AEV-T.2.4.1.2,a). -
Modulul
standardizat este modulul axial al melcului (modulul frontal al
roţii)mx = mx1 = mt2; modulul normal, mn = mx
cosγ; modulul frontal, mt1 = mx ctgγ
(fig. AEV-T.2.4.1.2,a). - Deplsările de profil ale danturilor roţilor se face din aceleaşi considerente ca la angrenajele cilindrice, cu deosebirea că acestea se fac numai la melc.
|
-
Raportul de
angrenare
(transmitere),
unde, d1,2 sunt diametrele cercurilor de divizare ale melcului, respectiv, roţii melcate; γ - ughiul elicei melcului; ω1,2 = v1,2/ (d1,2/2) - vitezele unghiulare ale melcului, respectiv, roţii; v1,2 - vitezele periferice ale melcului, respectiv, roţii melcate în polul angrenării (din fig. AEV-T.2.4.2.1, v2 = v1 ctg γ); n1,2 - turaţiile melcului, respectiv, roţii melcate; z1,2 - numerele de dinţi (începuturi) ai melcului, respectiv, roţii melcate. -
Unghiul elicei melcului,
unde, d1 este diametrul de divizare egal cu diametrul cilindrului de referinţă al melcului pentru angrenajul cu dantură nedeplasată (d1 = d01 = mx1 q); px1 = π mx1 - pasul axial al melcului; mx1 = mx - modulul axial al melcului (valori standard); q = z1/tgγ - factorul diametral al melcului cu valori standard în funcţie de modulul axial mx (ex., q = 9, 10, 11 sau 12 pentru mx = 3...8 mm) . -
Diametrele cercurilor de divizare
(melc şi roată melcată),
unde x este coeficientul deplasării profilului melcului. Obs. Angrenajul melcat globoidal, comparativ cu angrenajul melcat cilindric, se caracterizează printr-o funcţionare mai silenţioasă şi o portanţă mărită, dar are un randament mai scăzut şi prezintă dificultăţi de ordin tehnologic în realizarea melcului şi a montajului; se utilizează în construcţia transmisiilor cu gabarit redus (de ex. în casetele de direcţie ale autovehiculelor) |
|
a b Fig. AEV-T.2.4.1.1
Angrenajul elicoidal cilindric: a – vedere spaţială; b –
vedere axială |
|
|
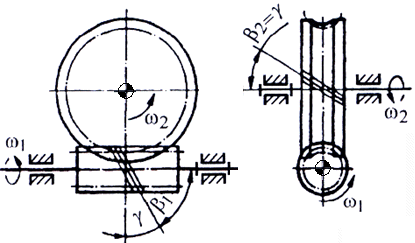
a b c Fig. AEV-T.2.4.1.3 Angrenaje cu axe încrucişate ortogonale: a – cilindric elicoidal; b – melcat cilindric; b – melcat globoidal |
|
AEV-T.2.4.2 MODELAREA ÎNCĂRCĂRILOR [Rădulescu, 1985]
|
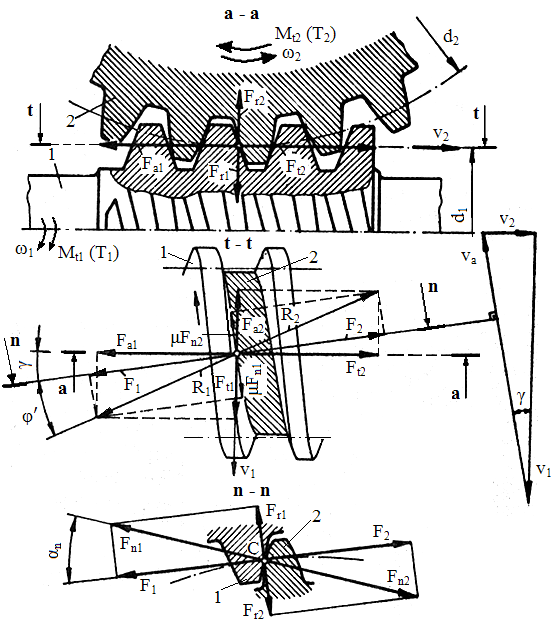
Fig. AEV-T.2.4.2.1 Schema
forţelor angrenajului melcat (a-a
secţiune axială; n-n
secţiune normală; t-t
secţiune tangenţială) |
Ipoteze simplificatoare: -
forţele
normale se consideră aplicate în polul angrenării, -
forţele
se consideră aplicate static. |
||
|
Tab. AEV-T.2.4.2.1 Relaţiile de calcul a forţelor |
|||
|
Parametrul
şi relaţia de calcul |
Direcţia
şi sensul |
||
|
Forţele tangenţiale şi axiale,
|
Direcţia, tangentă la cercul de rostogolire; Ft1,2, acelaşi sens cu viteza melcului, respectiv, roţii melcate; Fa1,2, sens opus vitezei roţii, respectiv, sens opus vitezei melcului |
||
|
Forţa normală,
|
|
||
|
Forţa radială, Fr = Fr1 = Fr2,
|
Direcţie radială; sensul spre axa melcului, respectiv, roţii |
||
|
Forţa de frecare,
Unghiul de frecare redus,
|
Forţa de frecare are aceeaşi direcţie cu viteza relativă, va, şi sensul opus acesteia |
||
|
Obs. |
a. Randamentul angrenajului,
b. În cazul simplificat, considerând frecarea neglijabilă (µ = 0, φ'=0), relaţiile de calcul a forţelor de mai sus devin:
c. Semnificaţii ale parametrilor geometrici din fig.AEV-T.2.4.2.1: γ – unghiul elicei melcului; d1,2 - diametrele cercurilor de divizare ale melcului respectiv roţii melcate; αn - unghiul de angrenare în plan normal; φ' - unghiul de frecare; ω1,2 - viteza unghiulară a melcului, respectiv, roţii melcate; Mt1,2 sau T1,2 – momentul de torsiune al melcului, respectiv, roţii melcate; v1,2 - vitezele periferice ale melcului, şi respectiv, roţii melcate (în polul angrenării) |
||
AEV-T.2.4.3 MODEL DE CALCUL A TENSIUNII DE CONTACT
Tab. AEV-T.2.4.3.1 Definirea şi parametrii modelului de calcul la contact[Jula, 1989;
Rădulescu, 1985; Moldovean, 2001]]
|
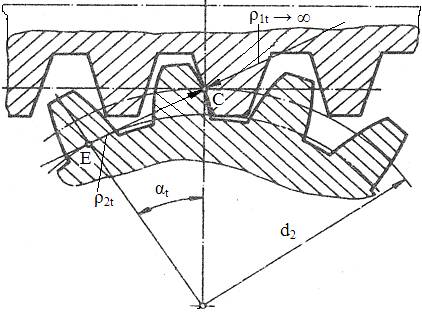
Fig. AEV-T.8.4.3.1 Modelul geometric de calcul a tensiunii de contact |
Calculul la solicitarea de contact se face prin analogie cu cel al angrenajelor cilindrice în condiţiile aceloraşi ipoteze de calcul folosind modelul lui Hertz, conform rel. (AEV-T.2.1.2.1) din subcap. AEV-T.2.1.2 în care, forţa normală de calcul (considerând forţa Fn din tab. AEV-T.2.4.2.1, fără frecare),
(KHα = 1; γ lungimea liniei de contact a unui
dinte al roţii melcate (fig.
AEV-T.2.4.1.2),
(2δ curbura redusă (fig. AEV-T.2.4.3.1) ,
|
Calculul la contact se face prin intermediul angrenajului cilindric cu dantură dreaptă. Relaţiile de calcul la contact se obţin prin înlocuirea parametrilor de calcul a angrenajului (tab. AEV-2.4.3.1) în relaţia lui Hertz de calcul a tensiuii de contact (AEV-T. 2.1.2). După efectuarea calculelor, ţinând cont şi de relaţiile de calcul a paramerrilor geometrici (subcap. AEV-T.2.4.1), se obţin relaţiile tensiunii maxime de contact a roţii melcate din tabelul următor.
Tab. AEV-T.2.4.3.2 Relaţii de calcul la contact a angrenajul melcat cilindric
|
Tensiunea de contact |
Dimensionare |
Verificare |
||
|
|
(AEV-T.2.4.3.4) |
|
(AEV-T.2.4.3.5) |
σHP2 – tensiunile admisibile la contact pentru pinion şi roată; SHmin – factorul minim de siguranţă la contact (fer. AEV-M.1); ZN2 – factorii numerelor ciclurilor de solicitare ale pinionului şi roţii (fer. AEV-F.13); ZR – factorul rugozităţilor flancurilor (fer. AEV-F.11); ZL – factorul lubrifiantului (fer. AEV-F.12); Zv – factorul de viteză (fer. AEV-F.10); Zw – factorul durităţilor (fer. AEV-F.9); Zx – factorul de mărime (fer. AEV-F.8) |
|
|
(AEV-T.2.4.3.6) |
|
(AEV-T.2.4.3.7) |
|
|
|
(AEV-T.2.4.3.8) |
|
(AEV-T.2.4.3.9) |
|
|
Obs.
|
||||
AEV-T.2.4.4 MODEL DE CALCUL AL TENSIUNILOR DE ÎNCOVOIERE
Calculul la încovoiere se face, de asemenea, prin intermediul angrenajului cilindric cu dantură înclinată. Roata melcată se consideră o roată dinţată cilindrică cu dantură înclinată. Relaţiile de calcul la încovoiere se obţin prin înlocuirea parametrilor angrenajului melcat în relaţiile de calcul a tensiunii maxime de încovoiere a roţii unui angrenaj cilindric cu dantură înclinată din tab. AEV-T. 2.2.4.2. După efectuarea calculelor, considerând Ysa2 =1, KFα = 1 şi ţinând cont şi de relaţiile de calcul a paramerrilor geometrici (subcap. AEV-T.2.4.1), se obţine relaţia de calcul a tensiunii maxime de contact a roţii melcate din tabelul următor.
Tab. AEV-T.2.4.4.1 Relaţii
de calcul
la încovoiere
a angrenajului melcat cilindric
|
Tensiunea maximă de încovoiere (2- roată
melcată) |
Verificare |
|
|
|
(AEV-T.2.4.4.1) |
σFlim2 – tensiunea limită la încovoiere pentru pinion şi roată (fer. AEV-M.1); SFmin – factorul minim de siguranţă la încovoiere (fer. AEV-F.1); YN2 – factorii numerelor ciclurilor de solicitare ale pinionului şi roţii (fer. AEV-F.13), YST – factorul tensiunii de încovoiere de refererinţă (YST=2); Yδ2 – factorii concentratorilor de tensiuni ai pinionului şi roţii (fer. AEV-F.15); YR2 – factorii rugozităţilor racordărilor pinionului şi roţii (fer. AEV-F.11), Yx – factorul de mărime petru încovoiere (fer. AEV-F.8). |
AEV-T.2.4.5 MODEL DE CALCUL TERMIC
|
Ecuaţia de
bilanţ termic,
în care,
P1 [kW] este puterea transmisă; kt [W/m2grad] – factorul de
transfer a căldurii (8…10, pentru circulaţie slabă a
aerului; 14…16, pentru circulaţie intensă a aerului; 20…26, pentru
răcire cu ventilator; 93…210, pentru răcirea uleiului cu ajutorul
serpentinei); S [m2] – suprafaţa de răcire a carcasei
(plus 50 % din suprafaţa nervurilor, dacă există); ψ – coeficientul
transmiterii căldurii prin suprafețele de rezemare a carcasei
(uzual, ψ < 0,3); tu
[oC] – temperatura uleiului; t0 [oC]
– temperatura mediului ambiant. |
Verificare |
Dimensionare |
|
Temperatura
uleiului,
unde, tumax
= 60o…70oC , temperatura admisibilă a uleiului |
Suprafaţa
carcasei necesară,
Factorul de transfer necesar,
|
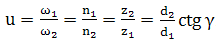
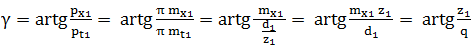

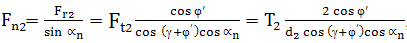
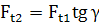 ;
;