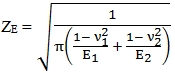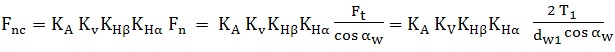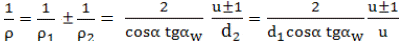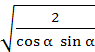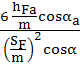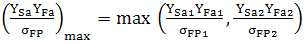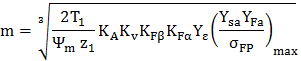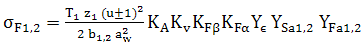AEV. ANGRENAJE EVOLVENTICE

AEV-T. STRUCTURA, CONSTRUCŢIA ŞI MODELAREA ANGRENAJELOR EVOLVENTICE

AEV-T.2 MODELAREA ANGRENAJELOR EVOLVENTICE

AEV-T.2.1 MODELAREA ANGRENAJELOR CILINDRICE CU DANTURĂ DREAPTĂ

 

            CUPRINS

AEV-T.2.1.1 MODELAREA ÎNCĂRCĂRILOR

AEV-T.2.1.2 MODEL DE CALCUL A TENSIUNII DE CONTACT

AEV-T.2.1.3 MODEL DE CALCUL A TENSIUNILOR DE  ÎNCOVOIERE 

 

 

 

 

AEV-T.2.1.1 MODELAREA ÎNCĂRCĂRILOR

 

Tab. AEV-T.2.1.1.1  Relaţii de calcul a forţelor din angrenajul cilindric cu dantură dreaptă

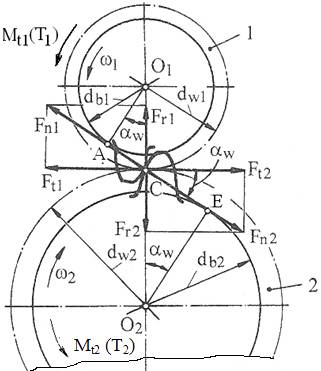
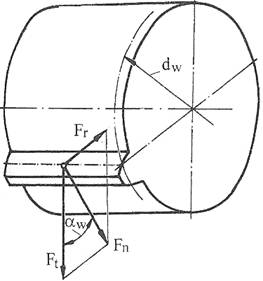
Ipoteze simplificatoare:

-         forţele normale se consideră aplicate în polul angrenării C la mijlocul roţii (fig. AEV-T.2.1.1.1,b),

-         se neglijează frecările,

-         se consideră forţele aplicate static.

Tab. AEV-T.2.1.1.1  Relaţiile de calcul a forţelor

Forţa

Relaţia

Direcţia şi sensul

Forţa tangenţială,

Ft = Ft1= Ft2

                         (AEV-T.2.1.1.1)

Direcţie tangentă la cercurile  de rostogolire; sens opus vitezei (forţă rezistentă), pentru roata conducătoare, şi acelaşi sens cu viteza (forţă motoare), pentru roata condusă

Forţa radială,

Fr = Fr1= Fr2

 (AEV-T.2.1.1.2)

 

Direcţie radială; sensul spre centrul roţii

Forţa normală,

Fn = Fn1= Fn2

Fn =  =

 

()              (AEV-T.2.1.1.3)

Direcţie după normala comună a profilelor în contact;  sens opus vitezei (forţă rezistentă), pentru roata conducătoare, şi acelaşi sens cu viteza (forţă motoare), pentru roata condusă

a

b

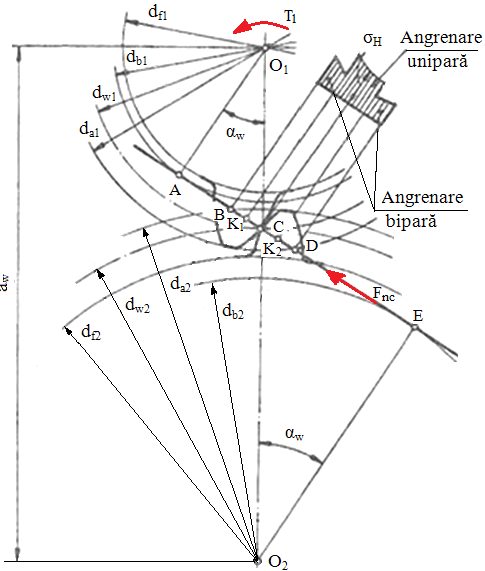
Fig. AEV-T.2.1.1.1  Schema forţelor [Moldovean, 2001]: a – în plan frontal, b - spaţial

Obs.

a.     Semnificaţiile parametrilor din fig. AEV-T.2.1.1.1: dw1,2 - diametrele cercurilor de rostogolire;   db1,2 - diametrele cercurilor de bază; αw - unghiul de angrenare real; ω1,2 - vitezele unghiulare; Mt1 sau T1 – momentul de torsiune al pinionului;  Mt2  sau T2 - momentul de torsiune al roţii.

b.     Pentru angrenajul nedeplasat (αw= α; dw1 = d1):  ,   ,    ;  α – unghiul de presiune, d1- diametrul de divizare al pinionului.

 

 

AEV-T.2.1.2 MODEL DE CALCUL A TENSIUNII DE CONTACT

 

Tab. AEV-T.2.1.2.1  Modelul şi relaţia de calcul la contact [Jula, 1989; Moldovean, 2001; Rădulescu, 1985]

a 

 

b

 c

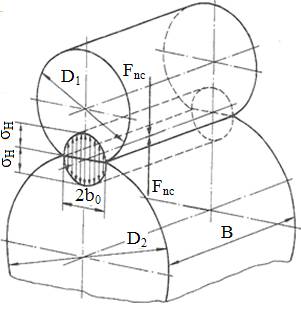
 Fig. AEV-T.2.1.2.1  Model de calcul la contact al angrenajului cilindric cu dantură dreaptă: a – modelul de calcul de referinţă (Hertz), b – modelul de calcul spaţial c – modelul de calcul în plan frontal

Modelul de calcul la contact de referinţă [Hertz, 1881] ( fig. AEV-T.2.1.2.1,a)

În zona de contact a doi cilindri cu diametrele D1,2 şi lungimi B, încărcaţi cu forţa Fnc, apar tensiuni maxime normale de contact care, conform lui Hertz, se determină cu relaţia,

  ,                                                                             (AEV-T.2.1.2.1)

 

în care, lk = B, reprezintă lungimea liniei de contact;

   =    =    ,

 

curbura redusă (ρ1,2 sunt razele de curbură ale celor doi cilindri,  semnul  (+) corespunde contactului exterior (fig. AEC-T.1,a), iar semnul  (-)  contactului interior;

,

factorul de elasticitate unde E1,2 şi ν1,2 sunt modulele de elasticitate şi,

respectiv, coeficienţii contracţiei transversale (Poisson) ai materialelor celor doi cilindri (fer. AEV-F.1).

Ipotezele modelului lui Hertz:

-         materialele cilindrilor sunt omogene, izotrope, elastice după legea lui Hooke;

-         forţa normală este aplicată static;

-         tensiunile de contact se repartizează uniform pe lungimea de contact;

-         lăţimea suprafeţei de contact 2b0, ca rezultat al deformării elastice este foarte mică în raport cu dimensiunile cilindrilor;

-         suprafeţele cilindrilor sunt perfect netede;

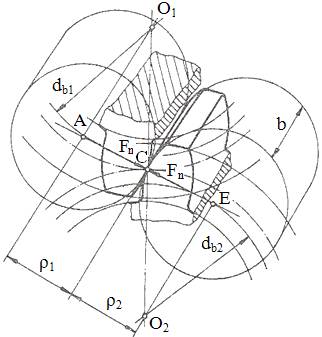
-         nu se iau în considerare forţele de frecare.

Diferenţe între modelul a doi dinţi în angrenare (fig. AEV-T.1, b ) şi modelul lui Hertz:

-         razele de curbură ale dinţilor sunt variabile (profilele sunt evolvente);

-         forţa de interacţiune dintre dinţi nu acţionează static ci variabil dependent de sarcinile dinamice exterioare şi interne;

-         tensiunile de contact nu sunt uniforme de-a lungul liniei de contact datorită impreciziilor, de execuţie şi montaj şi deformaţiilor elastice ale elementelor angrenajului;

-         există forţe de frecare;

-         flancurile nu sunt perfecte, pot avea  rugozităţi diverse.

Personalizarea parametrilor din relaţia lui Hertz pentru angrenajul deplasat  cu dinţi drepţi în contact în polul angrenării:

Forţa normală de contact,
 (AEV-T.2.1.2.2

 

KA – factorul regimului de funcţionare, ia în considerare efectul sarcinilor exterioare variabile (fer. AEV-F.2); Kv – factorul dinamic interior, ia în considerare sarcinile dinamice interioare (AEV-F.3); KHβ – factorul distribuţiei neuniforme a sarcinii de-a lungul liniei de contact, specific solicitării de contact, ia în considerare erorile de execuţie de la direcţia dintelui şi deformaţiile elastice ale elementelor subansamblului angrenajului (AEV-F.4);  KHα -  factorul repartizării neuniforme a sarcinii în plan frontal, specific solicitării de contact, ia în considerare erorile de pas (fer. AEV-F.5).

 Curbura redusă

Ţinând cont că,

  şi ;

  (d1,2 -diametrele de divizare, u=d2/d1),  rezultă,


                            (AEV-T.2.1.2.3)

 

Lungimea liniei de contact,

,                                                                                                (AEV-T.2.1.2.4)

unde b este lăţimea danturii (lungimea dintelui, grosimea roţii); Zε – factorul gradului de acoperire specific solicitării de contact (fer. AEV-F.6)

 

Tab. AEV-T.2.1.2.2 Relaţii de calcul la contact (forme extinse ale relaţiei de calcul de bază (AEV-T.2.1.2.1))

Tensiunea maximă de contact

Verificare

Dimensionare

 

(AEV- T.2.1.2.5)

 ,        (AEV-T.2.1.2.8)

 

 , 

 

σHP1,2 – tensiunile admisibile la contact pentru pinion şi, respectiv, roată;

σHlim – tensiunea limită la contact (fer. AEV-M.1);

SHmin – factorul minim de siguranţă la contact  (fer. AEV-F.14)

Zx – factorul dimensional (fer. AEV-F.8);

Zw – factorul durităţilor (fer. AEV-F.9);

Zv – factorul de viteză    (fer. AEV-F.10);

ZR – factorul rugozităţilor flancurilor (fer. AEV-F.11);

ZL – factorul lubrifiantului (fer. AEV-F.12);

ZN1,2 – factorii numerelor ciclurilor de solicitare ale pinionului şi roţii (fer. AEV-F.13);

 – tensiunea admisibilă la contact a angrenajului

 

(AEV- T.2.1.2.9)

 

(AEV- T.2.1.2.6)

 

(AEV- T.2.1.2.10)

 

(AEV- T.2.1.2.7)

 

 

(AEV- T.2.1.2.11)

Obs.

a.  În relaţiile din acest tabel  =   este factorul zonei de contact (fer. AV-F.7);    m – modulul danturii  (fer. AEV-P.1.4), z1 - numărul de dinţi ai pinionului (fer. AEV-P.1.1); ,  ,  - factori de lăţime raportaţi la distanţa dintre axe, modul şi, respectiv, diametrul pinionului (fer. AEV-P.1.3); pentru simplificarea relaţiilor de calcul se consideră cosα/cosαw  1

b.  Pentru angrenajul nedeplasat (dw1= d1; αw=α):  ;  d1= m z1 (v. fer AEV-T.8.1) ;  =   (fer. AEV-F.7).

 

 

AEV-T.2.1.3 MODEL DE CALCUL A TENSIUNIILOR DE ÎNCOVOIERE

 

Tab. AEV-T.2.1.3. Modelul şi relaţia de calcul de bază la încovoiere [Jula, 1989; Rădulescu, 1985; Moldovean, 2001]

 

 

 

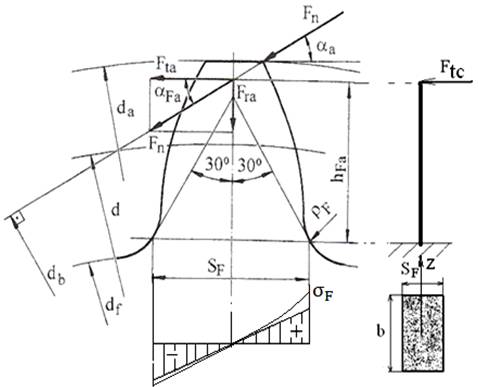
Fig. AEV- T.2.1.3.1 Model de calcul la încovoiere al angrenajului cilindric cu dantură dreaptă

Ipoteze simplificatoare:

-         dintele se consideră o bară dreaptă  solicitată la încovoiere luând în considerare concentratorul de tensiune de la baza dintelui (fig. AEV-T.2.1.3.1),

-         forţa normală se consideră concentrată la vârful dintelui,

-         se neglijează solicitarea de compresiune generată de forţa radială,

-         grosimea de calcul a dintelui se consideră determinată de două tangente la pofilele de racordare care fac 30o cu axa dintelui.

Forţa teoretică de calcul la încovoiere (fig. AEV-T.2.1.3.1),

  ,       (AEV- T.2.1.3.1)

 

unde KA – factorul regimului de funcţionare, ia în considerare efectul sarcinilor exterioare (fer. AEV-F.2); Kv – factor dinamic interior, ia în considerare sarcinile dinamice interioare (fer. AEV-F.3); KFβ – factorul distribuţiei neuniforme a sarcinii de-a lungul liniei de contact, specific solicitării de încovoiere, ia în considerare erorile de execuţie de la direcţia dintelui şi deformaţiile elastice ale elementelor subansamblului angrenajului (fer. AEV-F.4);  KFα -  factorul repartizării neuniforme a sarcinii în plan frontal, specific solicitării de încovoiere, ia în considerare erorile de pas (fer. AEV-F.5).

Relaţia de calcul de referinţă a tensiunii maxime de încovoiere, 

   =  =  ,                                    (AEV- T.2.1.3.2)

cu     , factorul de formă (fer. AEV-F.7); Yε – factorul gradului de acoperire pentru

 

solicitarea de încovoiere (fer. AEV-F.6); YSa – factorul de concentrare a tensiunilor de încovoiere la baza dintelui  (fer. AEV-F.15)

 

Tab. AEV-T.2.1.3.2  Relaţii de calcul la încovoiere (forme extinse ale relaţiei de calcul de bază (AEV- T.2.1.3.2))

Tensiunile maxime de încovoiere (1 – pinion, 2- roată)

Verificare

Dimensionare

 

 

(AEV- T.2.1.3.3)

,   (AEV- T.2.1.3.7)

 

,

 

σFP1,2 – tensiunile admisibile la încovoiere pentru pinion şi roată;

σFlim1,2 – tensiunea limită la încovoiere pentru pinion şi roată (fer. AEV-M.1);

SFmin – factorul minim de siguranţă la încovoiere (fer. AEV-F.1);

YN1,2 – factorul numerelor ciclurilor de solicitare ale pinionului şi roţii (fer. AEV-F.13),

YST – factorul tensiunii de încovoiere de refererinţă (YST=2);

Yδ1,2 – factorii concentratorilor de tensiuni ai pinionului şi roţii (fer. AEV-F.15);

YR1,2 – factorii rugozităţilor racordărilor pinionului şi roţii (fer. AEV-F.11);

Yx – factorul de mărime al angrenajului pentru încovoiere (fer. AEV-F.8)

 

(AEV- T.2.1.3.8)

 

(AEV- T.2.1.3.4)

 

 

 

 

 

(AEV- T.2.1.3.9)

 

 

(AEV- T.2.1.3.5)

 

 

(AEV- T.2.1.3.10)

Obs.

a.        Pentru angrenajul nedeplasat (dw1=d1; αw=α; aw=a): ;  d1= m z1  (fer. AEV-F.11); m – modulul danturii (fer. AEV-P.1.4), z1 - numărul de dinţi ai pinionului (fer. AEV-P.1.1); 

 

b.         În relaţiile din acest tabel: ,  ,  - factori de lăţime raportaţi la distanţa dintre axe, modul şi, respectiv, diametrul pinionului (fer. AEV-P.1.3)