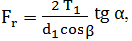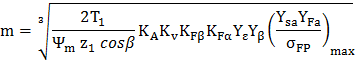AEV. ANGRENAJE EVOLVENTICE
AEV-T. STRUCTURA, CONSTRUCŢIA ŞI MODELAREA ANGRENAJELOR EVOLVENTICE
AEV-T.2 MODELAREA ANGRENAJELOR EVOLVENTICE
AEV-T.2.2 MODELAREA ANGRENAJELOR CILINDRICE CU DANTURĂ ÎNCLINATĂ
|
CUPRINS |
|
AEV-T.2.2.1 PARTICULARITĂŢI GEOMETRICE ŞI FUNCŢIONALE ALE ANGRENAJELOR CILINDRICE CU DANTURĂ ÎNCLINATĂ AEV-T.2.2.2 MODELAREA ÎNCĂRCĂRILOR AEV-T.2.2.3 MODEL DE CALCUL AL TENSIUNII DE CONTACT AEV-T.2.2.4 MODEL DE CALCUL AL TENSIUNII DE ÎNCOVOIERE |
AEV-T.2.2.1 PARTICULARITĂŢI GEOMETRICE ŞI FUNCŢIONALE ALE ANGRENAJELOR CILINDRICE CU DANTURĂ ÎNCLINATĂ
Tab. AEV-T.2.1.1.1 Particularităţi geometrice, funcţionale şi constructive [Jula, 1989; Rădulescu, 1985; Moldovean, 2001]
|
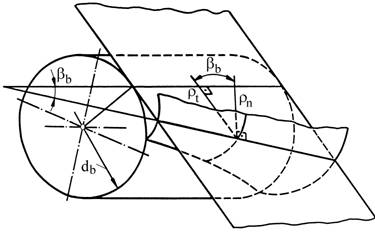
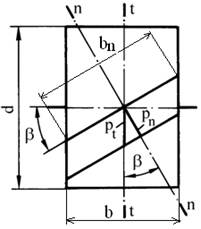
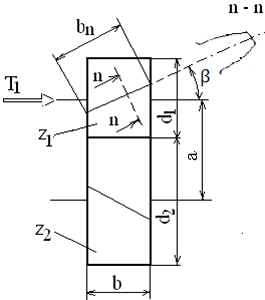
a b
Fig. AEV-T.2.2.1.1 Caracteristicile geometrice principale ale profilului evolventic înclinat: a - vedere spaţială; b – vedere axială |
Particularităţi geometrice |
|
- Flancul dintelui se generează prin deplasarea unei drepte înclinată cu unghiul βb în raport cu generatoarea cilindrului de bază (fig. AEV-T.2.2.1.1,a). Dependenţa dintre razele de curbură ale evolventei (profilului) în plan normal n-n, ρn, şi, cea în plan frontal t-t, ρt, este
ρn = ρt cosβb. (AEV-T.2.2.1.1)
- Dependenţa dintre pasul danturii în plan frontal pt şi cel în plan normal pn (fig. AEV-T.2.2.1.1,b) este pn = pt cosβ; ţinând cont că p = mt π, rezultă dependenţa dintre modulul frontal mt şi mn,
mn = mt cosβ, (AEV-T.2.2.1.2)
cu β unghiul de înclinare a danturii; Obs. în practica de proiectare, de obicei, parametrii geometrici în plan frontal nu conţin indicele t (mt = m, pt = p, ρt = ρ etc.) |
|
|
Particularităţi constructive şi funcţionale |
|
|
- Lungimea dintelui este mai mare decât lăţimea roţii (rezistenţă la încovoiere este mai mare decât în cazul dintelui drept). - Dinţii înclinaţi intră şi ies progresiv în şi, respectiv, din angrenare fapt, ce conduce la zgomote reduse şi, deci, utilizarea pentru viteze mai mari. - Există mai multe perechi de dinţi în angrenare; gradul de acoperire total, εγ = εα+ εβ, εα – gradul de acoperire în plan frontal, εβ - gradul de acoperire suplimentar, datorat înclinării danturii. |
AEV-T.2.2.2 MODELAREA ÎNCĂRCĂRILOR [Rădulescu, 1985]
|
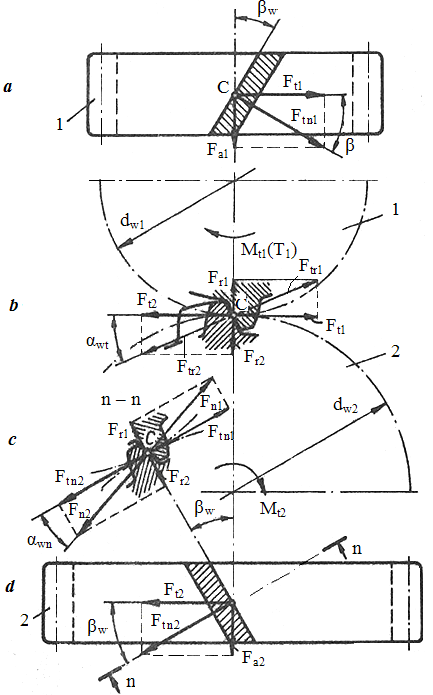
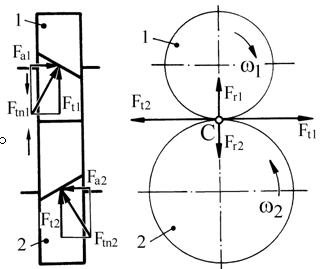
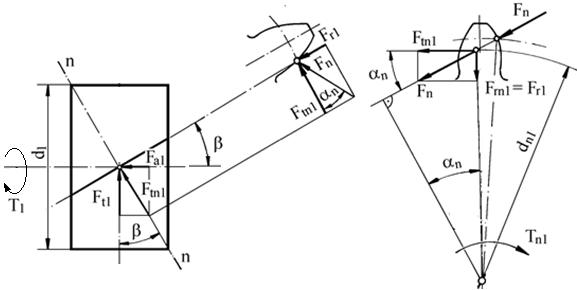
Fig. AEV-T.2.2.2.1 Schema forţelor : a – în plan axial pentru pinion, b – în plan frontal pentru angrenaj; c – în plan normal pentru angrenaj; d - în plan axial pentru roată; e – vedere spaţială |
Ipoteze simplificatoare: - forţele normale se consideră aplicate în polul angrenării C la mijlocul lăţimii roţilor (fig. AEV-T.8.2.2.1) - se neglijează frecările, - forţele se consideră aplicate static |
|||
|
Tab. AEV-T.2.2.2.1 Relaţiile de calcul a forţelor |
||||
|
Parametrul |
Relaţia |
Direcţia şi sensul (fig. AEV-T.2.2.2.2) |
||
|
Forţa tangenţială, Ft = Ft1= Ft2 |
|
Direcţie tangentă la cercurile de rostogolire; sens opus vitezei (forţă rezistentă), pentru roata conducătoare, şi acelaşi sens cu viteza (forţă motoare), pentru roata condusă |
||
|
Forţa radială, Fr = Fr1= Fr2 |
|
Direcţie radială; sensul spre centrul roţii; tgαwt = tgαwn/cosβw |
||
|
Forţa axială, Fa = Fa1= Fa2 |
|
Direcţie axială; sensul determinat de direcţia de înclinare a dintelui şi de sensul de rotaţie al roţii |
||
|
Forţa normală, Fn = Fn1= Fn2 |
Fn =
(AEV-T.2.2.2.4)
( |
Direcţie după normala comună a profilelor în contact; sens opus vitezei (forţă rezistentă), pentru roata conducătoare, şi acelaşi sens cu viteza (forţă motoare), pentru roata condusă |
||
|
e |
Obs. 1 Pentru angrenajul nedeplasat (αwn= αn = α; βw = β; dw1= d1):
α = αn – unghiul de angrenare de referinţă, d1 - diametrul de divizare al pinionului; β – unghiul de înclinare a danturii |
|||
|
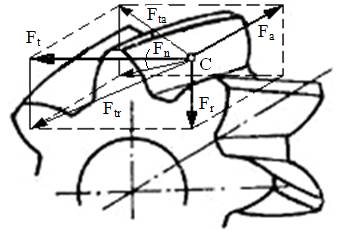
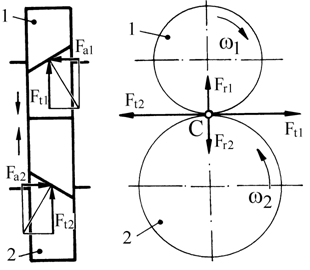
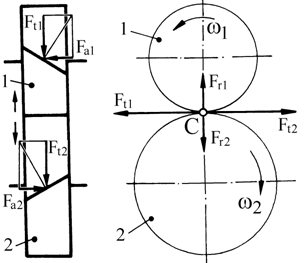
a b c Fig. AEV-T.2.2.2.2 Direcţiile şi sensurile forţelor din angrenajele cilindrice cu dantură înclinată: a – mişcarea în sens orar şi înclinarea danturii spre dreapta; b – mişcarea în sens orar şi înclinarea danturii spre stânga; c – mişcarea în sens antiorar şi înclinarea danturii spre dreapta [Moldovean, 2001]
Obs. 2 Semnificaţiile parametrilor geometrici din fig. AEV-T.2.2.2.1: dw1,2 - diametrele cercurilor de rostogolire; βw – unghiul de înclinare al danturii pe cercul de rostogolire; αwt - unghiul de angrenare în plan frontal; αwn - unghiul de angrenare în plan normal; ω1,2 - vitezele unghiulare; Mt1 sau T1 – momentul de torsiune al pinionului; Mt2 - momentul de torsiune al roţii; Ftn – forţa normală în plan tangenţial (Ftn = Ftn1 = Ftn2) |
||||
AEV-T.2.2.3 MODEL DE CALCUL A TENSIUNII DE CONTACT
Tab. AEV-T.2.2.3.1 Definirea şi parametrii angrenajului echivalent [Jula, 1989; Rădulescu, 1985; Moldovean, 2001]
|
|
|
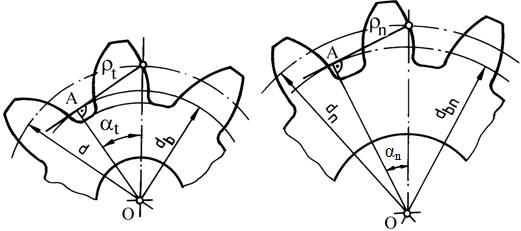
Definire angrenaj echivalent (fictiv, virtual): Deoarece în planul normal la direcţia dintelui dimensiunile sunt minime şi, în plus, în acest plan acţionează forţa de interacţiune Fn, calculul angrenajului cilindric cu dantură înclinată se realizează prin intermediul unui angrenaj cilindric echivalent cu roţi echivalente (cu dantură dreaptă, fig. AEV-T.2.2.3.1,a,b), care are aceiaşi parametri geometrici şi de încărcare ca ai angrenajului real (cu dantură înclinată) în plan normal. Roata echivalentă este roata cu dantură dreaptă care are dinţii cu aceeași formă şi dimensiuni ca şi dinţii roţii reale în plan normal (de unde şi indicele n); pentru modelarea matematică se vor considera următoarele egalităţi: raza de curbură a profilului dintelui roţii echivalente este egală cu raza de curbură a profilului dintelui roţii reale în plan normal; modulul roţii echivalente este egal cu modulul normal al roţii reale; coeficientul deplasării de profil al roţii echivalente este egal cu coeficientul deplasării de profil de la roata reală în plan normal.
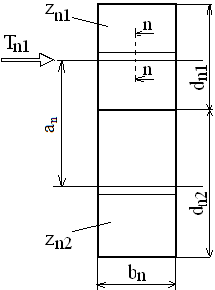
Parametrii angrenajului cilindric echivalent (pentru angrenajul înclinat nedeplasat): Diametrele cercurilor de divizare Din fig. AEV-T.2.2.3.1,c şi d rezultă d = 2 ρt sinαt şi, respectiv, dn=2 ρn sinα (relaţiile sunt generale, la nevoie, se pot personaliza pentru pinionul, 1 şi roata 2); ţinând cont de relaţia (AEV-T.2.2.1.1), rezultă
Numerele de dinţi ai roţilor Înlocuind în relaţia (AEV-T.2.2.3.1), dn = mn zn şi d = m z şi, în plus, ţinând cont de relaţia (AEV-T.2.2.1.2), rezultă
Distanţa dintre axe Ținând cont de rel. (AEV- T.2.2.3.1),
Raportul de angrenare Având în vedere rel. (AEV- T.2.2.3.3),
Momentul de torsiune al pinionului Ţinând cont de fig. AEV-T.2.2.3.2 şi relaţia (AEV-T.2.2.3.3), rezultă
Lăţimea danturii (fig. AEV-T.2.2.3.1,a,b)
|
|
a |
b |
|
|
|
||
|
c |
d |
|
|
Fig. AEV-T.2.2.3.1 Modelul de echivalare a angrenajului cilindric cu dantură înclinată cu un angrenaj cu dantură dreaptă: a - vedere axială a angrenajului cu dantură înclinată (real), b - vedere axială a angrenajului cu dantură dreaptă echivalent (virtual), c – vedere frontală pinion/roată cu dantură înclinată (reale); d – vedere frontală pinion/roată cu dantură dreaptă echivalent (virtuale)
a b Fig. AEV-T.2.2.3.2 Modelul de echivalare a momentului de torsiune: a - vedere axială şi secţiune normală a dintelui pinionului (real), b - vedere frontală a pinionului echivalent |
||
Calculul la contact al angrenajului cilindric cu dantură înclinată se face prin intermediul angrenajului cilindric cu dantură dreaptă echivalent.
Relaţiile de calcul (tab. AEV-T.2.2.3.2) la contact a angrenajului cilindric cu dantură înclinată obţinute prin înlocuirea parametrilor angrenajului echivalent (tab AEV-2.2.3.1) în relaţiile de calcul la contact a angrenajului cu dantura dreaptă din cap. AEV.T.2.1, tab. AEV-T. 2.1.2.2 sunt sintetizate în tab. AEV-T.2.2.3.2.
|
|
|||||||
|
Tensiunea de contact |
Verificare |
Dimensionare |
|||||
|
|
(AEV- T.2.2.3.7) |
σHP1,2 – tensiunile admisibile la contact pentru pinion şi roată, σHlim – tensiunea limită la contact (fer. AEV-M.1), SH min – factorul minim de siguranţă la contact (fer. AEV-F.1), ZN1,2 – factorii numerelor ciclurilor de solicitare ale pinionului şi roţii (fer. AEV-F.13), ZR – factorul rugozităţilor flancurilor (v fer. AEV-F.11), ZL – factorul lubrifiantului (fer. AEV-F.12), Zv – factorul de viteză (fer. AEV-F.10), Zw – factorul durităţilor (fer. AEV-F.9), Zx – factorul de mărime (fer. AEV-F.8)
|
|
(AEV- T.2.2.3.11) |
|||
|
|
(AEV- T.2.2.3.8) |
|
(AEV- T.2.2.3.12) |
||||
|
|
(AEV- T.2.2.3.9) |
|
(AEV- T.2.2.3.13) |
||||
|
Obs.
a.
Pentru angrenajul nedeplasat (dw1=d1;
αw =α):
b. În relaţiile din acest
tabel: c. Relaţiile de calcul pentru angrenajul cu dantură înclinată sunt cvasiaceleaşi cu cele pentru angrenajul cu dantură dreaptă cu deosebirea că, în plus, apare factorul Zβ; apar diferenţe şi în relaţiile de calcul a factorilor de corecţie (Zε, ZH) |
|||||||
AEV-T.2.2.4 MODEL DE CALCUL A TENSIUNILOR DE ÎNCOVOIERE
Calculul la încovoiere se face, de asemenea, prin intermediul angrenajului cilindric cu dantură dreaptă echivalent. Relaţiile de calcul la încovoiere (tab. AEV-T.2.2.4.1) se obţin prin înlocuirea parametrilor angrenajului echivalent (tab AEV-2.2.3.1) în relaţiile de calcul la încovoiere a angrenajului cu dantura dreaptă din cap. AEV.T.2.1, tab. AEV-T. 2.1.3.2.
Tab. AEV-T.2.2.4.1 Relaţii de calcul a tensiunilor de încovoiere
|
Tensiunile maxime de încovoiere (1 – pinion, 2- roată) |
Verificare |
Dimensionare |
||
|
|
(AEV- T.2.2.4.1) |
σFP1,2 – tensiunile admisibile la încovoiere pentru pinion şi roată; σFlim1,2 – tensiunea limită la încovoiere pentru pinion şi roată (fer. AEV-M.1); SFmin – factorul minim de siguranţă la încovoiere (fer. AEV-F.1); YN1,2 – factorul numerelor ciclurilor de solicitare ale pinionului şi roţii (fer. AEV-F.13), YST – factorul tensiunii de încovoiere de refererinţă (YST=2); Yδ1,2 – factorii concentratorilor de tensiuni ai pinionului şi roţii (fer. AEV-F.15); YR1,2 – factorii rugozităţilor racordărilor pinionului şi roţii (fer. AEV-F.11), Yx – factorul de mărime pentru încovoiere (fer. AEV-F.8); Yβ – factorul înclinării danturii pentru solicitarea de încovoiere (fer. AEV-F.9); |
|
(AEV- T.2.2.4.5) |
|
|
(AEV- T.2.2.4.2) |
|
(AEV- T.2.2.4.6) |
|
|
|
(AEV- T.2.2.4.3) |
|
(AEV- T.2.2.4.7) |
|
|
Obs.
a.
Pentru angrenajul nedeplasat (dw1=d1;
αw =α):
b.
În relaţiile din acest
tabel:
c.
Relaţiile de calcul pentru angrenajul cu dantură
înclinată sunt cvasiaceleaşi cu cele pentru angrenajul cu
dantură dreaptă cu deosebirea că, în plus, apare factorul Yβ
şi cosβ la numitorul fracţiilor. |