AEV. ANGRENAJE EVOLVENTICE
AEV-T. STRUCTURA, CONSTRUCŢIA ŞI MODELAREA ANGRENAJELOR EVOLVENTICE
AEV-T.2 MODELAREA ANGRENAJELOR EVOLVENTICE
AEV-T.2.3 MODELAREA ANGRENAJELOR CONICE (CU DANTURĂ DREAPTĂ, CURBĂ (ÎNCLINATĂ) ŞI HIPODĂ
|
CUPRINS |
|
AEV-T.2.3.1 PARTICULARITĂŢI GEOMETRICE ŞI FUNCŢIONALE ALE ANGRENAJELOR CONICE AEV-T.2.3.2 MODELAREA ÎNCĂRCĂRILOR ANGRENAJELOR CONICE AEV-T.2.3.3 MODEL DE CALCUL A TENSIUNII DE CONTACT DIN ANGRENAJELE CONICE AEV-T.2.3.4 MODEL DE CALCUL A TENSIUNILOR DE ÎNCOVOIERE DIN ANGRENAJELE CONICE AEV-T.2.3.5 PARTICULARITĂŢI DE CALCUL A ANGRENAGELOR HIPOIDE |
AEV-T.2.3.1 PARTICULARITĂŢI GEOMETRICE ŞI FUNCŢIONALE ALE ANGRENAJELOR CONICE [Rădulescu, 1985; Moldovean, 2001]
|
Aspecte generale |
Parametrii cinematici şi geometrici principali |
|
- Din punct de vedere al poziţiei spaţiale a axelor angrenajului general (tab. AEV-T.1.7.1), angrenajul conic are distanţa dintre axe a = 0 şi unghiul dintre acestea Σ ≠ 0.
-
Angrenajul conic este un
angrenaj sferic cu axoidele mişcării suprafeţe conice circulare cu
semiunghiurile δ1,2 (fig. AEV-T.2.3.1.1) şi unghiul dintre axe
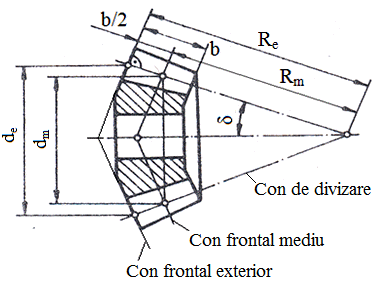
- În cazul execuţiei roţilor conice cu scule cu profil drept (muchii aşchietoare linii drepte) rezultă un profil neriguros evolventic cu cercul diametral de angrenare degenerat în octoidă, de unde şi denumirea de angrenaj octoidal. - Pentru definirea geometriei angrenajului conic, prin analogie cu a celui cilindric, se aproximează suprafaţele sferice cu suprafaţe conice frontale (desfăşurabile în plan) tangente la sfere (aproximaţia Tredgold). - Angrenajul conic, fiind un angrenaj evolventic aproximativ, poate fi numai nedeplasat sau zero-deplasat cu deplasări radiale şi/sau tangenţiale. - Parametrii geometrici de reprezentare în desenele de execuţie (cu implicaţii tehnologice) se definesc la nivelul conului frontal exterior (indice e, care în documentaţia tehnică poate lipsi), iar parametrii geometrici pentru calculul forţelor şi de rezistenţă se definesc la nivelul conului frontal mediu (indice m, fig. AEV-T.2.3.1.2). |
- Diametrele cercurilor de divizare medii (fig. AEV-T.2.3.1.2; 1 - pinion; 2 - roată conică),
cu - Modulul mediu , considerând în (AEV-T.2.3.1.2) dm1 = mm z1 şi de1 = me z1,
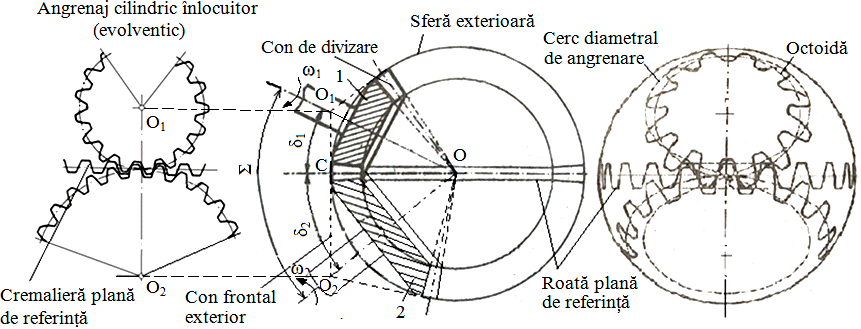
- Raportul de angrenare,
pentru angrenajul conic ortogonal cu Σ = δ1 + δ2 =90o,
u =1/tgδ1 = tg δ2 |
|
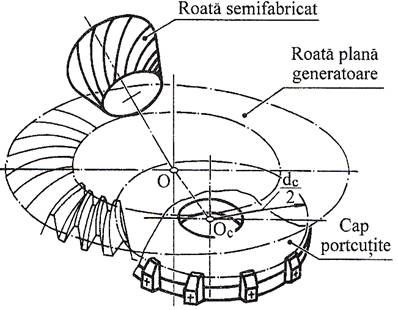
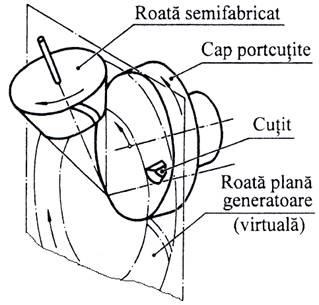
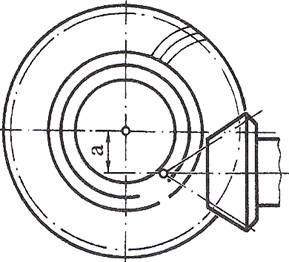
Obs. a. Angrenajele conice cu dantură dreaptă, din considerente de funcţionare fără vibraţii şi zgomote, sunt utilizate pentru viteze periferice reduse (v=2…3 m/s). b. Angrenajele conice cu dantură înclinată funcţionează la viteze periferice de până la 12 m/s, se execută pe aceleaşi maşini pe care se execută roţile cu dantură dreaptă, în condiţii de productivitate mult redusă şi, deci sunt utilizate rar în practică. c. Angrenajele conice cu dantură curbă funcţionează în condiţiii de silenţiozitate şi durabilitate mărite la viteze periferice mari (de până la 12 m/s), se execută pe maşini specializate de mare productivitate şi au parametrii geometrici dependenţi de procedeele tehnologice de danturare, de tipul maşinii şi sculei de danturat [Velicu, 2004]. - dantura curbă în arc de cerc (Gleason) se execută cu un cap portcuţite (fig. AEV-T.2.3.1.3,a) care are cuţitele de danturat cu muchii rectilinii, dispuse circular; contactul între flancurile dinţilor roţilor este teoretic punctiform; unghiul de înclinare median al danturii în arc de cerc, βm (uzual, 35o), este dependent de parametrii sculelor de danturat. - dantura curbă eloidă, uzual bazată pe procedeul Oerlikon-Spiromatic, are linia flancului dintelui roţii plane epicicloidă alungită ce se obţine prin utilizarea unui cap portcuţite care are cuţitele fixate pe spirale diferite pentru obţinerea unghiului de înclinare median al danturii, βm = 35o (fig. AEV-T.2.3.1.3,b) . d. Angrenajele conice cu axe încrucişate (hipoide) au axoidele (suprafeţele de rostogolire) hiperboloizi de rotaţie şi au raport de transmitere constant. Dantura roţilor hipoide este curbă (fig. AEVT.2.3.1.4) se prelucrează pe aceleaşi maşini de danturat ca şi pentru roţile angrenajelor concurente. |
|
|
|
Fig. AEV-T.2.3.1.2 Parametrii geometrici principali ai
unei roţii conice |
|
|
|
|
|
a |
b |
Fig. AEVT.2.3.1.4 Angrenaj hipoid |
|
Fig. AEV-T.2.3.1.3 Danturi conice curbe: a – în arc de cerc, b – eloidă [Velicu, 2004] |
||
AEV-T.2.3.2 MODELAREA ÎNCĂRCĂRILOR ANGRENAJELOR CONICE [Rădulescu, 1985]
|
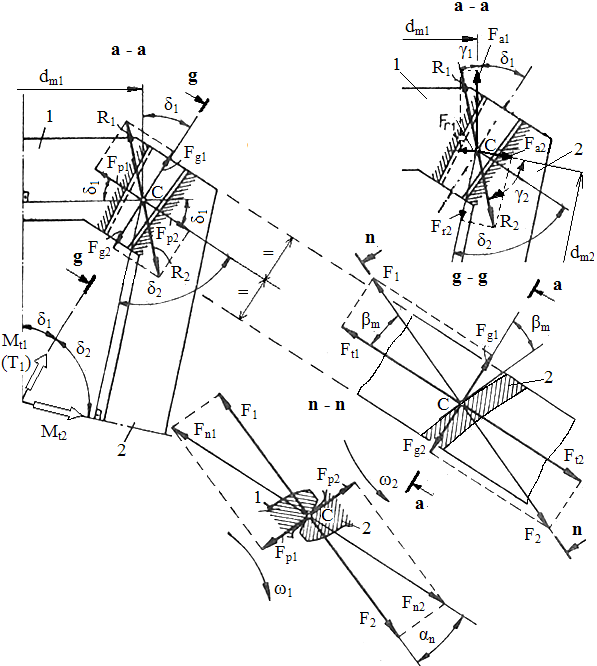
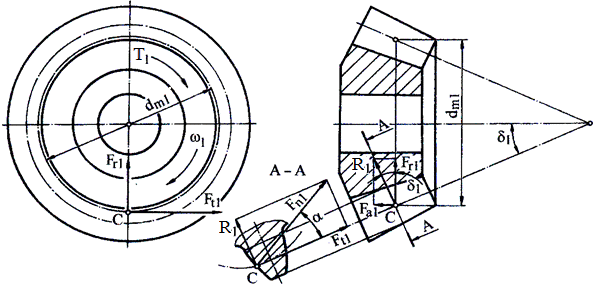
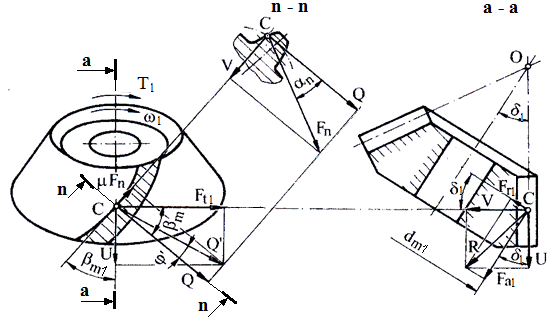
Fig. AEV-T.2.3.2.1 Schema forţelor angrenajului conic (a-a, secţiunea axială; n-n, secţiune normală; g-g, secţiune tangenţială după generatoare)
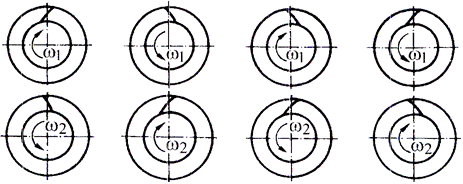
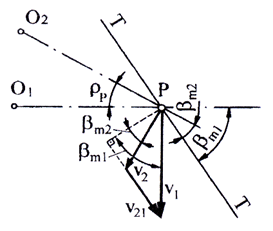
a b c d Fig. AEV-T.2.3.2.2 Sensurile de rotaţie a roţilor (pinionului) şi sensurile înclinării dinţilor acestuia: a – sensul de rotaţie orar, sensul înclinării dintelui spre dreapta; b – sensul de rotaţie antiorar, sensul înclinării dintelui spre stânga; c – sensul de rotaţie orar, sensul înclinării dintelui spre stânga; b – sensul de rotaţie antiorar, sensul înclinării dintelui spre dreapta
|
Ipoteze simplificatoare: -
forţele
normale se consideră aplicate în polul angrenării C asociat conului frontal
mediu, -
se
neglijează frecările, -
forţele
se consideră aplicate static. Tab. AEV-T.2.3.2.1 Determinarea forţelor |
||
|
Parametrul
şi relaţia de calcul |
Direcţia
şi sensul |
||
|
Forţele tangenţiale,
|
Direcţie tangentă la cercul de
rostogolire; sens opus vitezei (forţă rezistentă), pentru
roata conducătoare, şi acelaşi sens cu viteza (forţă motoare), pentru roata condusă |
||
|
Forţele radiale,
|
Direcţie radială; sensul spre axa roţii
|
||
|
Forţele axiale,
|
Direcţie
axială; sensul spre exterior |
||
|
Forţa normală,
|
Direcţie
după normala comună a profilelor în contact; sens opus vitezei, pentru roata conducătoare, şi acelaşi sens
cu viteza, pentru roata condusă |
||
|
a. Semnificaţiile parametrilor geometrici din fig. AEV-T.2.3.2.1: δ1,2 – semiunghiurile conurilor de divizare (rostogolire); dm1,2 - diametrele cercurilor de divizare medii; βm – unghiul de înclinare al danturii pe cercul de divizare mediu; αn - unghiul de angrenare în plan normal median; ω1,2- vitezele unghiulare; Mt1 (T1) – momentul de torsiune al pinionului conic; Mt2 - momentul de torsiune al roţii conice b. În relaţiile (AEV-T.2.3.2.2) ... (AEV-T.2.3.2.5): semnul superior este pentru situaţia în care sensul de rotaţie al pinionului este acelaşi cu sensul de înclinare a dinţilor acestuia (privind din vârful conului, fig. AEV-T.2.3.2.2, a,d); semnul inferior este pentru cazul în care sensul de rotaţie al pinionului este opus sensului de înclinare a dinţilor acestuia (privind din vârful conului), fig. AEV-T.2.3.2.2, b,c. În fig. AEV-T.2.3.2.1 este reprezentată schema forţelor pentru prima situaţie (sensurile aceleaşi), sensul de rotaţie a pinionului este orar şi sensul înclinării dintelui acestuia este spre dreapta; c. Cazuri particulare: |
|||
|
Angrenajul conic
neortogonal cu dantură dreaptă
( βm = 0; αn = α)
Ft1 = Ft2 = Ft; Fn1 = Fn2 = Fn |
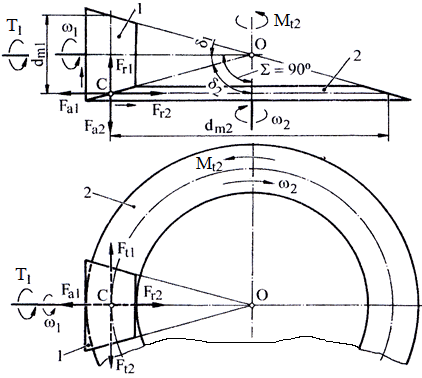
Angrenajul conic ortogonal cu dantură dreaptă ( βm = 0; αn = α; δ1+ δ2 = 90o; fig. AEV-T.2.3.2.3)
Ft1 = Ft2 = Ft; Fr1 = Fa2; Fa1 = Fr2; Fn1 = Fn2 = Fn |
||
|
a b Fig. AEV-T.2.3.2.3 Forţele angrenajului conic ortogonal cu dantură dreaptă: a – schema de încărcare a pinionului, b – schema forţelor angrenajului |
|||
Tab. AEV-T.2.3.3.1 Definirea şi parametrii angrenajului cilindric echivalent virtual
|
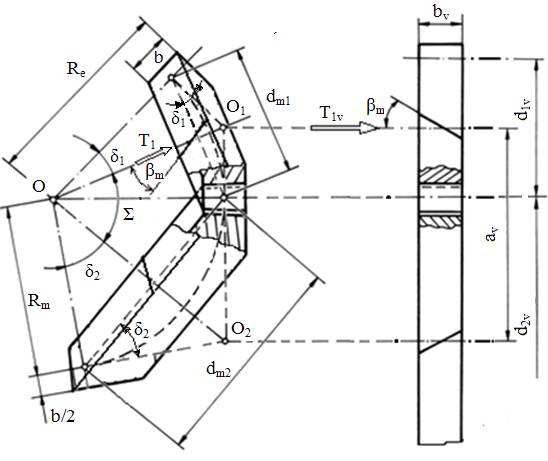
Definire angrenaj cilindric echivalent virtual şi roata echivalentă (fig. AEV-T.2.3.3.1): Calculul de rezistenţă al angrenajului conic cu dantură curbă (înclinată), considerând că în planul normal median acţionează forţa de interacţiune Fn, se efectuează în secţiunea mediană (conul frontal median) prin intermediul unui angrenaj cilindric echivalent (virtual, de unde şi indicele v) cu dantură înclinată. Roata echivalentă a angrenajului cilindric cu dantură înclinată echivalent are dinţii cu aceeași formă şi dimensiuni ca şi dinţii roţii conice reale în plan normal median; pentru modelarea matematică se vor considera următoarele egalităţi: - modulul normal al roţilor echivalente este egal cu modulul normal median al roţilor conice; - unghiul de înclinare a danturii roţilor echivalente este egal cu unghiul de înclinare de divizare median al danturii roţilor conice; - razele cercurilor de divizare ale roţilor echivalente sunt egale cu lungimile generatoarelor conurilor frontale mediane ale roţilor conice; - înălţimea dinţilor roţilor înlocuitoare este egală cu înălţimea dinţilor roţilor conice în secţiune mediană |
|
Fig. AEV-T.2.3.3.1 Modelul
de echivalare a angrenajului conic cu dantură înclinată
sau curbă cu un
angrenaj cilindric cu dantură înclinată |
Parmetrii angrenajului cilindric echivalent: Diametrele cercurilor de divizare,
Numerele de
dinţi, Înlocuind în rel.
(AEV-T.2.3.3.1), d1,2v = mm z1,2v, dm1,2 = mm z1,2 (modulul normal al roţii
echivalente este
egal cu modulul normal mediu), rezultă,
Raportul de
angrenare, Având în vedere rel.
(AEV-T.2.3.3.2),
Distanţa
dintre axe, Ţinînd cont de
rel. (AEV-T.2.3.3.2) şi, rezultă,
Momentul de
torsiune, Ținând cont de rel.
(AEV-T.2.3.3.2) rezultă,
Lăţimea danturii (fig. AEV-T.2.3.3.1),
b = bv
(AEV-T.2.3.3.6) |
Calculul la contact al angrenajului conic cu dantură curbă se face prin intermediul angrenajului cilindric cu dantură înclinată echivalent.
Relaţiile de calcul la contact (tab. AEV-T.2.3.3.2) se obţin prin înlocuirea parametrilor angrenajului echivalent (tab. AEV-2.3.3.1) în relaţiile de calcul la contact a angrenajului cilindric cu dantura înclinată din cap. AEV-T.2.2, tab. AEV-T. 2.2.3.2.
|
Tab. AEV-T.2.3.3.2 Relaţii de calcul la contact a angrenajelor conice |
||||||
|
Tensiunea de contact |
Dimensionare |
Verificare |
||||
|
Cazul general. Angrenaj conic
neortogonal cu dantură curbă (înclinată) (Σ ≠
90,
βm ≠ 0) |
σHP1,2 – tensiunile
admisibile la contact
pentru pinion şi roată; σHlim – tensiunea
limită la contact (fer. AEV-M.1); SH min – factorul
minim de siguranţă la contact (fer. AEV-F.1);
ZN1,2
– factorii
numerelor
ciclurilor de solicitare
ale pinionului şi roţii
(fer. AEV-F.13); ZR – factorul
rugozităţilor flancurilor (fer. AEV-F.11); ZL – factorul
lubrifiantului (fer. AEV-F.12); Zv – factorul
de viteză (fer. AEV-F.10);
Zw – factorul
durităţilor (fer. AEV-F.9); Zx – factorul
de mărime (fer. AEV-F.8) |
|||||
|
|
(AEV-T.2.3.3.7) |
|
(AEV-T.2.3.3.8) |
|||
|
Cazul particular 1. Angrenaj conic ortogonal cu dantură curbă (înclinată) (Σ = 90, βm ≠ 0) |
||||||
|
|
(AEV-T.2.3.3.9) |
|
(AEV-T.2.3.3.10) |
|||
|
Cazul particular 2. Angrenaj conic neortogonal cu
dantură dreaptă (Σ ≠ 90,
βm = 0) |
||||||
|
|
(AEV-T.2.3.3.11) |
|
(AEV-T.2.3.3.12) |
|||
|
Cazul particular 3. Angrenaj conic ortogonal cu dantură dreaptă (Σ = 90, βm = 0) |
||||||
|
|
(AEV-T.2.3.3.13) |
|
(AEV-T.2.3.3.14) |
|||
|
Obs. |
a.
z1 este numărul de dinţi al pinionului
(fer. AEV-P.1.1); b.
Tensiunile de contact, menţionate în coloana 1, precum
şi relaţiile de dimensionare, din coloana 2, se pot
determina în funcţie de modulul exterior, me, sau de
lungimea generatoarei exterioare, Re, ca urmare a folosirii
relaţiei
|
|||||
AEV-T.2.3.4 MODEL DE CALCUL A TENSIUNILOR DE ÎNCOVOIERE DIN ANGRENAJELE CONICE
Calculul la încovoiere al angrenajului conic cu dantură curbă se face, de asemenea, prin intermediul angrenajului cilindric cu dantură înclinată echivalent.
Relaţiile de calcul la încovoiere (tab. AEV-T.2.3.4.1) se obţin prin înlocuirea parametrilor angrenajului echivalent (tab. AEV-2.3.3.1) în relaţiile de calcul la contact a angrenajului cu dantura înclinată din cap. AEV-T.2.2 tab. AEV-T. 2.2.4.1.
Tab. AEV-T.2.3.4.1 Relaţii de calcul la încovoiere pentru angrenajul conic
|
Tensiunile maxime de încovoiere (1 – pinion, 2- roată) |
Dimensionare |
Verificare |
|||
|
Cazul general. Angrenaj conic neortogonal
cu dantură curbă (înclinată) (Σ
≠ 90, βm ≠ 0) |
σF1
σFP1,2 – tensiunile
admisibil la încovoiere pentru pinion şi roată; σFlim1,2
– tensiunea limită la încovoiere pentru pinion şi roată (fer. AEV-M.1); SFmin – factorul
minim de siguranţă la încovoiere
(fer. AEV-F.1); YN1,2 – factorul numerelor ciclurilor de solicitare ale pinionului şi roţii (fer. AEV-F.13), YST – factorul tensiunii de încovoiere de refererinţă (YST=2); Yδ1,2 – factorii concentratorilor de tensiuni ai pinionului şi roţii (fer. AEV-F.15); YR1,2 – factorii rugozităţilor racordărilor pinionului şi roţii (fer. AEV-F.11), Yx – factorul
de mărime petru încovoiere (fer. AEV-F.8) |
||||
|
|
(AEV- T.2.3.4.1) |
|
(AEV- T.2.3.4.2) |
||
|
Cazul particular 1. Angrenaj conic ortogonal cu dantură
curbă (înclinată) (Σ =90, βm ≠ 0) |
|||||
|
|
(AEV- T.2.3.4.3) |
|
(AEV- T.2.3.4.4) |
||
|
Cazul particular 2. Angrenaj conic neortogonal cu dantură dreaptă (Σ ≠ 90, βm = 0) |
|||||
|
|
(AEV- T.2.3.4.5) |
|
(AEV- T.2.3.4.6) |
||
|
Cazul particular 3. Angrenaj conic ortogonal cu dantură dreaptă (Σ = 90, βm = 0) |
|||||
|
|
(AEV- T.2.3.4.7) |
|
(AEV- T.2.3.4.8) |
||
|
Obs.
a.
z1
este numărul de dinţi al pinionului
(fer. AEV-P.1.1);
b.
Tensiunile de contact, menţionate în coloana 1, precum
şi relaţiile de dimensionare din coloana 2 se pot explicita în funcţie de modulul
exterior, me, sau de lungimea generatoarei exterioare,
Re,
ca urmare a folosirii relaţiei de1
= me z1
sau, respectiv,
de1
= 2 Re
sin δ1. |
|||||
AEV-T.2.3.5 PARTICULARITĂŢI DE CALCUL A ANGRENAGELOR HIPOIDE
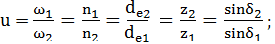
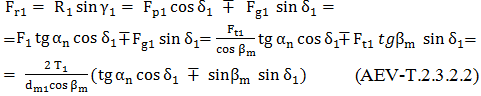
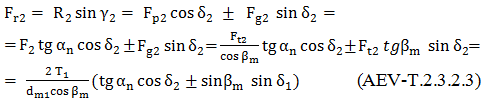
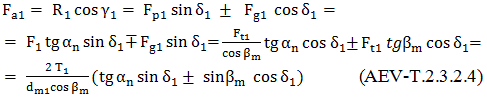
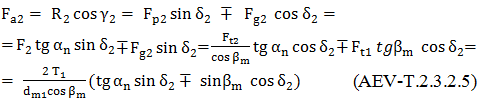
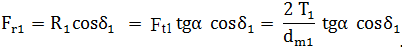 ,
,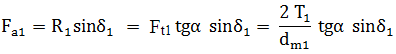
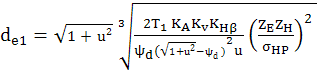
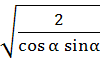
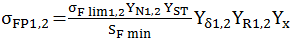
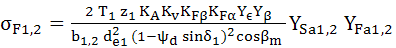
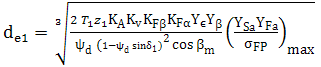
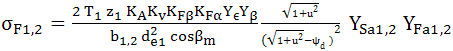
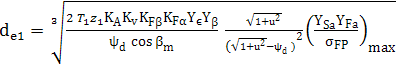
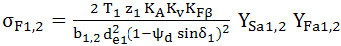
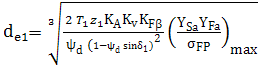
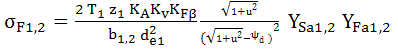
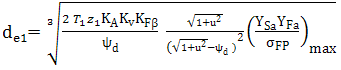
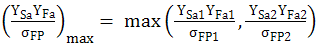 ; Y
; Y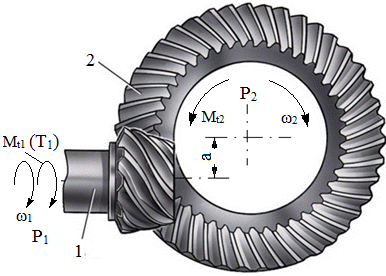
 35o,
uzual se folosesc valori apropiate de 35o , iar pentru
pinion, β
35o,
uzual se folosesc valori apropiate de 35o , iar pentru
pinion, β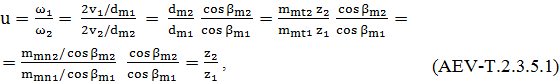
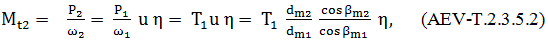
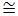 1,2…1,3
evidenţiază creşterea dimensiunilor (rigidităţii) pinionului;
1,2…1,3
evidenţiază creşterea dimensiunilor (rigidităţii) pinionului;