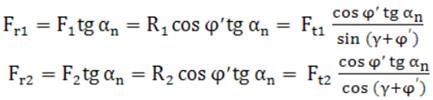…autori… Organe de Mașini. Lucrări de laborator. Universitatea Transilvania din Braşov
	Lucrarea LD.OM II.04 FORȚE ȘI MOMENTE ÎN TRANSMISII CU ANGRENAJE
CUPRINS
A. DESCRIEREA TEMATICII B. FORȚELE DIN ANGRENAJELE CU ROȚI DINȚATE C. FORȚELE DIN TRANSMISIILE CU ANGRENAJE
A. DESCRIEREA TEMATICII
A.1 Aspecte generale
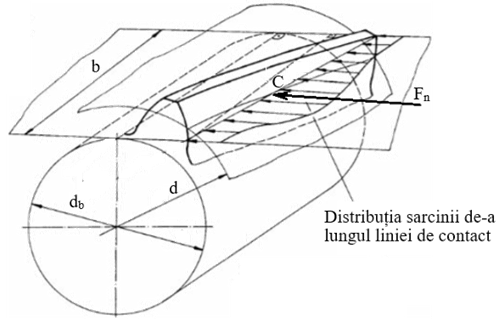
Angrenajele transmit sarcina prin contactul direct dintre dinții roților, între care apar forțe de interacțiune, normale la profilele dinților, egale şi de sens opus. Forțele normale Fn ca forțe distribuite pe linia de contact se consideră aplicate în polul angrenării C, la mijlocul lățimii roții, pe cilindrii de rostogolire (divizare). Pentru calculul arborilor şi a lagărelor (rulmenților) care susțin roțile dințate, este necesară cunoaşterea acestor forțe şi, în majoritatea cazurilor, a componentelor acestora:  tangențială, Ft, tangentă la cercul de rostogolire; radială, Fr, perpendiculară pe axa roții; axială, Fa, paralelă cu axa roții. Pentru determinarea acestor forțe, este necesar să se stabilească momentul de torsiune Mt1 la arborele de intrare (motor, antrenor) în funcție de parametrii caracteristici de antrenare: puterea motorului, P, şi turația, n.
A.2 Scopul lucrării
Prin efectuarea lucrării de laborator se urmărește cunoașterea tipurilor forțelor din angrenajele, roți dințate și arbori: - determinarea valorilor, direcțiilor și  sensurilor forțelor din angrenajele reductoarelor de turație;   - determinarea valorilor, direcțiilor și  sensurilor forțelor care încarcă arborii reductoarelor de turație
B. FORȚELE DIN ANGRENAJELE CU ROȚI DINȚATE
B.1 Forțele din angrenajele cilindrice
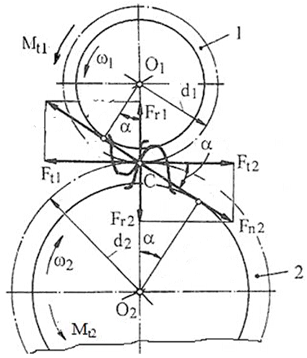
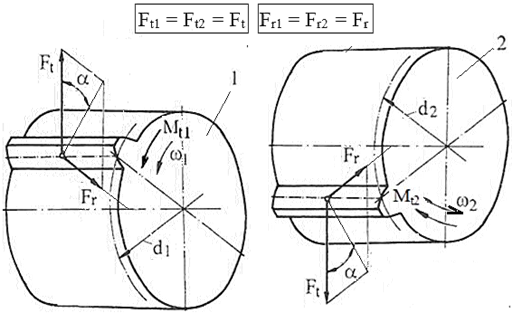
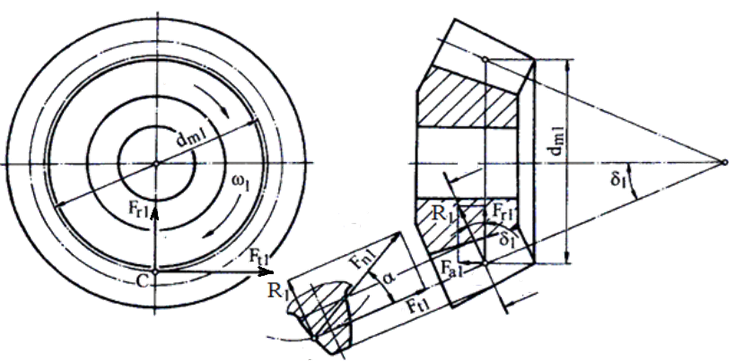
Direcțiile si sensurile forțelor din angrenajele cilindrice https://rrv.unitbv.ro/RConCil/Anexe/Anexa.7.1.1 Directiile si sensurile fortelor din angrenaje.htm Forțe în angrenajul și în roțile  dințate cilindrice cu dantură dreaptă nedeplasată  Semnificații parametrii:   1 – pinion cilindric, 2 – roată cilindrică, ω1 [rad/s] – viteza unghiulară a pinionului, ω2 [rad/s] – viteza unghiulară a roții, Ft1 [N] – forța tangențială a pinionului; Ft2 [N] – forța tangențială a roții; Fr1 [N] – forța radială a pinionului; Fr2 [N] – forța radială a roții; Fa1 [N] – forța axială a pinionului; Fa2 [N] – forța axială a roții; Mt1 [Nmm] – momentul de torsiune al pinionului; Mt2 [Nmm] – momentul de torsiune al roții; d1 [mm] – diametrul de divizare al pinionului, d2 [mm] – diametrul de divizare al roții, α [^o , grade] – unghiul de angrenare (presiune) (α = 20^o). Relații de calcul: Forța tangențială, Ft = 2Mt1/d1. Forța radială, Fr = Ft tg α. 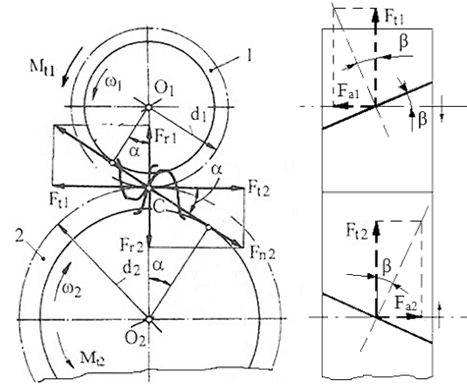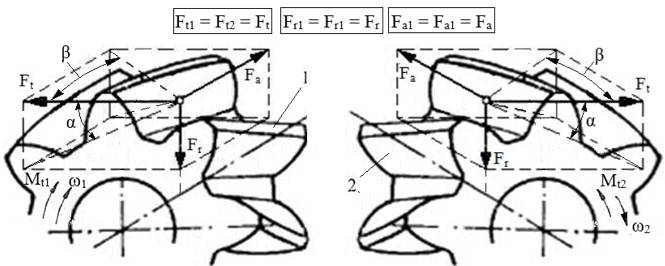Forțe în angrenajul și în roțile  dințate cilindrice cu dantură înclinată nedeplasată Semnificații notații: 1 – pinion cilindric, 2 – roată cilindrică, ω1 [rad/s] – viteza unghiulară a pinionului, ω2 [rad/s] – viteza unghiulară a roții, Ft1 [N] – forța tangențială a pinionului; Ft2 [N] – forța tangențială a roții; Fr1 [N] – forța radială a pinionului; Fr2 [N] – forța radială a roții; Fa1 [N] – forța axială a pinionului; Fa2 [N] – forța axială a roții; Mt1 [Nmm] – momentul de torsiune al pinionului; Mt2 [Nmm] – momentul de torsiune al roții; d1 [mm] – diametrul de divizare al pinionului, d2 [mm] – diametrul de divizare al roții, α [^o] – unghiul de angrenare (presiune), β [^o] – unghiul de înclinare a danturilor la nivelul cercurilor de divizare. Relații de calcul: Forța tangențială, Ft = 2Mt1/d1. Forța radială, Fr = Ft tg α =  Ft tg αn /cos β. Forța axială, Fa = Ft tg β. Obs. Pentru roțile cu dantură înclinată, unghiul de angrenare (presiune) în plan normal, αn = 20^o și tg α = tg αn /cos β. Pentru determinarea forțelor din angrenajul cilindric cu dantură înclinată deplasată se poate urmări modelul de la adresa: https://rrv.unitbv.ro/RCil/Subcapitole/Subcap.7.3 Forte in angrenajul cilindric.htm
B.2 Forțele din angrenajele conice
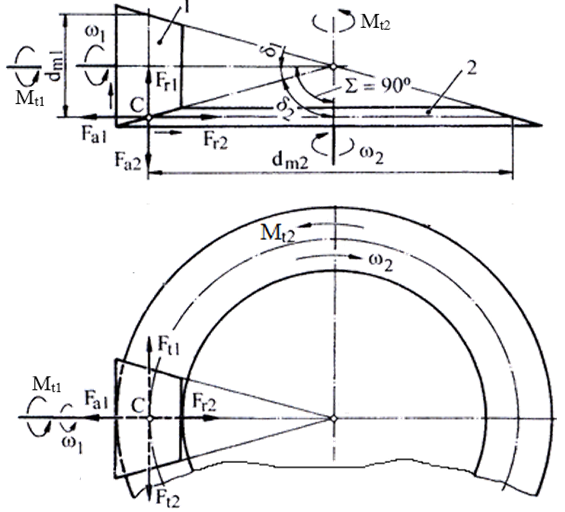
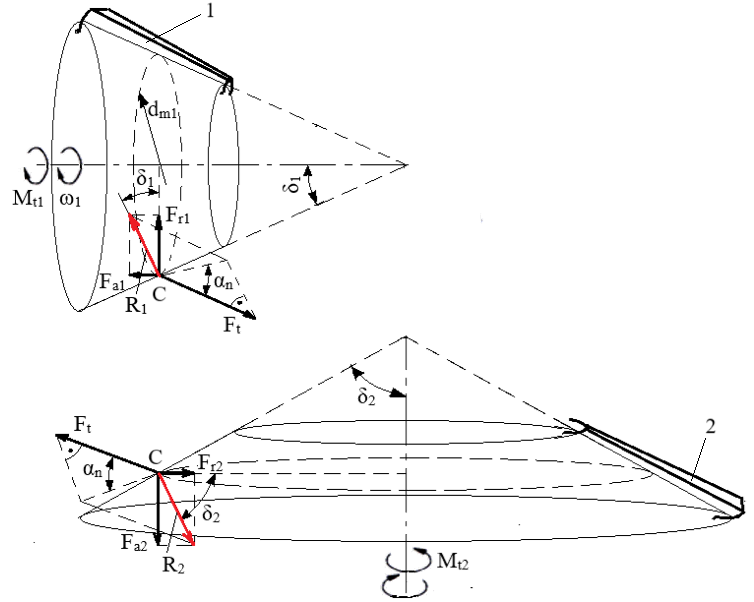
Direcțiile si sensurile forțelor din angrenajele conice https://rrv.unitbv.ro/RConCil/Anexe/Anexa.7.1.1 Directiile si sensurile fortelor din angrenaje.htm Forțe în angrenajul conic ortogonal cu dantură dreaptă Semnificații notații:   1 – pinion conic, 2 – roată conică, ω1 [rad/s] – viteza unghiulară a pinionului, ω2 [rad/s] – viteza unghiulară a roții, Ft1 [N] – forța tangențială a pinionului; Ft2 [N] – forța tangențială a roții; Fr1 [N] – forța radială a pinionului; Fr2 [N] – forța radială a roții; Fa1 [N] – forța axială a pinionului; Fa2 [N] – forța axială a roții; R1 [N] – forța normală pe generatoare conului de divizare al pinionului;  R2 [N] – forța normală pe generatoarea conului de divizare al roții; Mt1 [Nmm] – momentul de torsiune al pinionului; Mt2 [Nmm] – momentul de torsiune al roții; dm1 [mm] – diametrul de divizare mediu al pinionului, dm2 [mm] – diametrul de divizare mediual roții, αn [^o] – unghiul de angrenare (presiune) (αn = 20^o), δ1 [^o] – semiunghiul conului de divizare al pinionului, δ2 [^o] – semiunghiul conului de divizare al roții Obs. Conform principiului acțiunii și reacțiunii: Ft1 = Ft2 = Ft; Fr1 = Fa2;  Fr2 = Fa1; R1 = R2 = R. Relații de calcul: Forța tangențială, Ft = 2Mt1/dm1. Forțale radiale, Fr1 = R cos δ1 = Ft tg αn cos δ1, Fr2 = R cos δ2 = Ft tg αn cos δ2. Forțale axiale, Fa1 = R sin δ1 = Ft tg αn sin δ1, Fa2 = R sin δ2 = Ft tg αn sin δ2. Obs.  Deoarece, δ1 + δ2 =90^o, sin δ2 = cos δ1, cos δ2 = sin δ1 rezultă și matematic că: Fr1 = Fa2, Fa1 = Fr2. Forțe în angrenajul conic ortogonal cu dantură curbă https://rrv.unitbv.ro/RConCil/Subcapitole/Subcap.7.2.1 Forte in angrenajul conic.htm
B.3 Forțele din angrenajele melcate
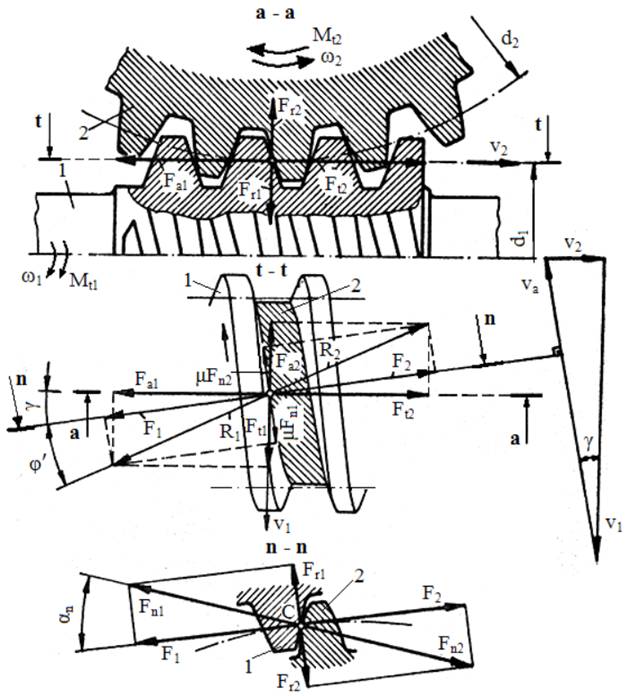
Schema forțelor din angrenajul melcat Semnificații notații:   αn [^o ]  -  unghiul de angrenare în plan normal; µ - coieficientul de frecare; φ' [^o ] - unghiul de frecare redus; ω1 [rad/s] – viteza unghiulară a melcului; ω2 [rad/s] – viteza unghiulară a roții melcate; v1 [mm/s] – viteza periferică a melcului; v2 [mm/s] – viteza periferică a roții melcate; Mt1 [Nmm] – momentul de torsiune al melcului; Mt2 [Nmm] – momentul de torsiune al roții melcate; γ [^o ] – unghiul elicei melcului; d1 [mm] – diametrul de divizare al melcului; d2 [mm] – diametrul de divizare al roții melcate; Fn1 [N] – forța normală a melcului; Fn2 [N] – forța normală a roții melcate; Fa1 [N] – forța axială a melcului; Fa2 [N] – forța axială a roții melcate;  Fr1 [N] – forța radială a melcului; Fr2 [N] – forța radială a roții melcate;  F1 [N] – forța normală a melcului în plan axial; F2 [N] – forța normală a roții melcate în plan axial; R1 [N] – rezultanta forței normale și celei de frecare asociată melcului; R2 [N] – rezultanta forței normale și celei de frecare asociată roții melcate; Obs.  Fn1 = Fn2 = Fn; Ft2 = Fa1;  Ft1 = Fa2; F1 = F2 = F;  R1 = R2 = R;  Relații de calcul: Forțele tangențiale și axiale, Ft1 = Fa2 = , Ft2 = Fa1 =  . Forțele radiale, , unde, Pentru cazul simplificat, frecarea neglijabilă (µ = 0, φ'=0), , .
C. FORȚE DIN TRANSMISIILE CU ANGRENAJE
C.1 Forțe din angrenajele reductoarelor
Forțelor din angrenajele reductoarelor cilindrice Forţele din angrenajul cilindric al RCil H: https://rrv.unitbv.ro/RCil/Subcapitole/Subcap.7.1 Schema fortelor din angrenajul RCil H.htm Forţele din angrenajul cilindric al RCil H: https://rrv.unitbv.ro/RCil/Subcapitole/Subcap.7.2 Schema fortelor din angrenajul RCil V.htm Forțe din angrenajele reductoarelor conico-cilindrice Forțele din reductorul conico-cilindric HH: https://rrv.unitbv.ro/RConCil/Subcapitole/Subcap.7.1.1 Schema fortelor din angrenajele RconCil HH.htm Forțele din reductorul conico-cilindric VV: https://rrv.unitbv.ro/RConCil/Subcapitole/Subcap.7.1.2 Schema fortelor din angrenajele RconCil VV.htm Forțele din reductorul conico-cilindric HV: https://rrv.unitbv.ro/RConCil/Subcapitole/Subcap.7.1.3 Schema fortelor din angrenajele RconCil HV.htm Forțele din reductorul conico-cilindric VH: https://rrv.unitbv.ro/RConCil/Subcapitole/Subcap.7.1.4 Schema fortelor din angrenajele RconCil VH.htm
C2.  Forțele de încărcare a arborilor
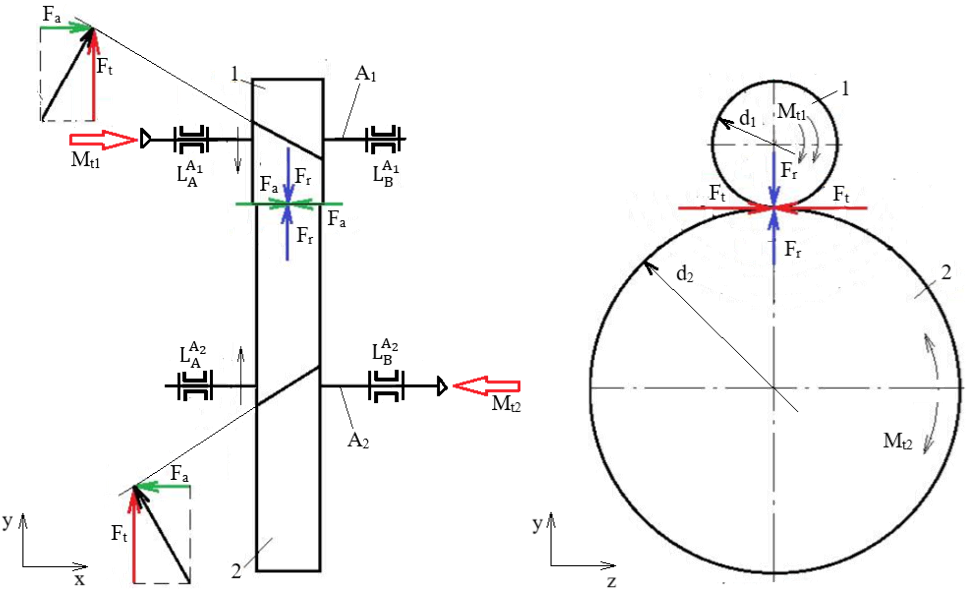
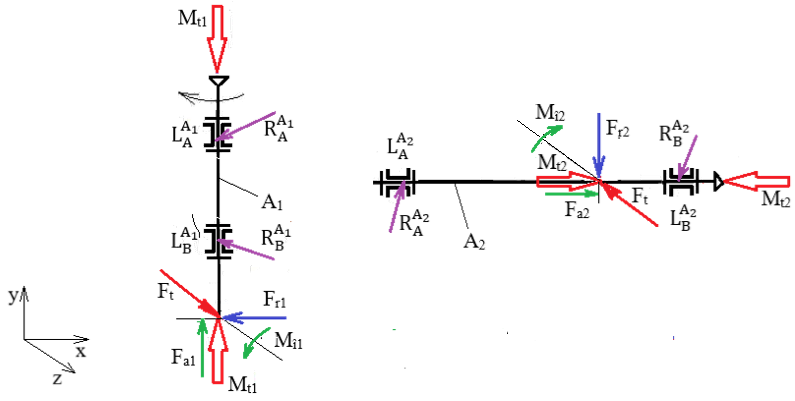
Forțele de încărcare a arborilor unui reductor cilindric cu dantură înclinată Semnificații parametrii:   1 – pinion cilindric, 2 – roată cilindrică,  A1 – arbore de intrare, A2 – arbore de ieșire,   – lagărul (rulmentul) A al arborelui A1,   – lagărul (rulmentul) B al arborelui A1, – lagărul (rulmentul) A al arborelui A2,  – lagărul (rulmentul) B al arborelui A2, Ft [N] – forța tangențială, Fr [N] – forța radială, Fa [N] – forța axială; Mt1 [Nmm] – momentul de torsiune al arborelui de intrare; Mt2 [Nmm] – momentul de torsiune al arborelui de ieșire; Mî1 [Nmm] – momentul de încovoiere al pinionului cilindric; Mî2 [Nmm] – momentul de încovoiere al roții cilindrice; [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A1,  [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A1,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A2, [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A2, d1 [mm] – diametrul de divizare al pinionului cilindric, d2 [mm] – diametrul de divizare al roții cilindrice, β [^o] – unghiul de înclinare a danturilor la nivelul cercurilor de divizare. 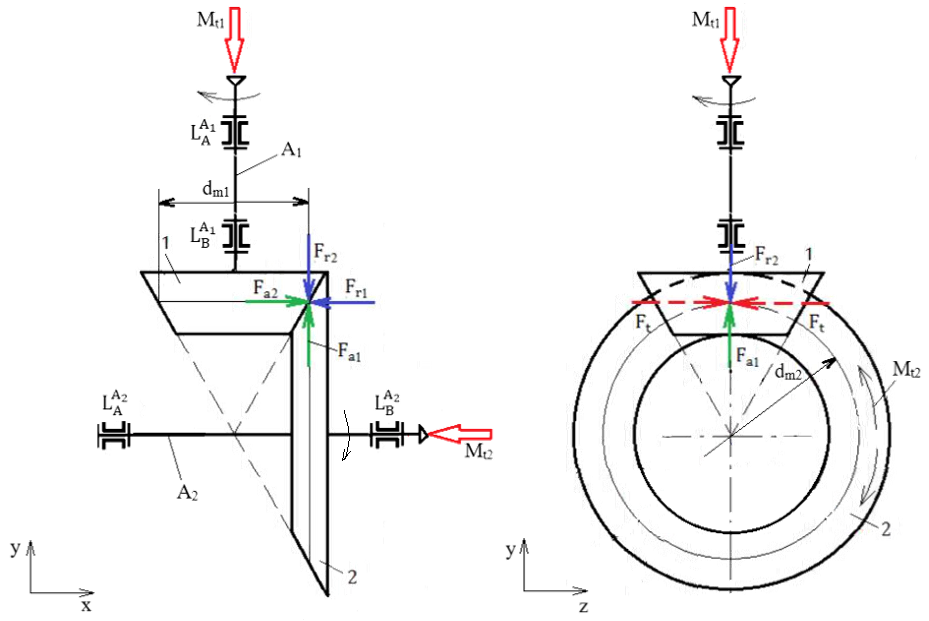Valorile momentelor de încovoiere: Mî1 =  Fa d1/2;  Mî2 =  Fa d2/2; Forțele de încărcare a arborilor unui reductor conic    Semnificații parametrii:   1 – pinion conic, 2 – roată conică,  A1 – arbore de intrare, A2 – arbore de ieșire,   – lagărul (rulmentul) A al arborelui A1,  – lagărul (rulmentul) B al arborelui A1, – lagărul (rulmentul) A al arborelui A2,  – lagărul (rulmentul) B al arborelui A2, Ft [N] – forța tangențială, Fr1 [N] – forța radială a pinionului conic, Fa1 [N] – forța axială a pinionului conic; Fr2 [N] – forța radială a roții conice (Fr2= Fa1), Fa2 [N] – forța axială a roții conice (Fa2= Fr1); Mt1 [Nmm] – momentul de torsiune al arborelui de intrare; Mt2 [Nmm] – momentul de torsiune al arborelui de ieșire; Mî1 [Nmm] – momentul de încovoiere al pinionului conic; Mî2 [Nmm] – momentul de încovoiere al roții conice; [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A1,  [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A1,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A2, [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A2, dm1 [mm] – diametrul de divizare mediu al pinionului conic, dm2 [mm] – diametrul de divizare mediu al roții conice. Valorile momentelor de încovoiere: Mî1 =  Fa1 d1/2;  Mî2 =  Fa2 d2/2.   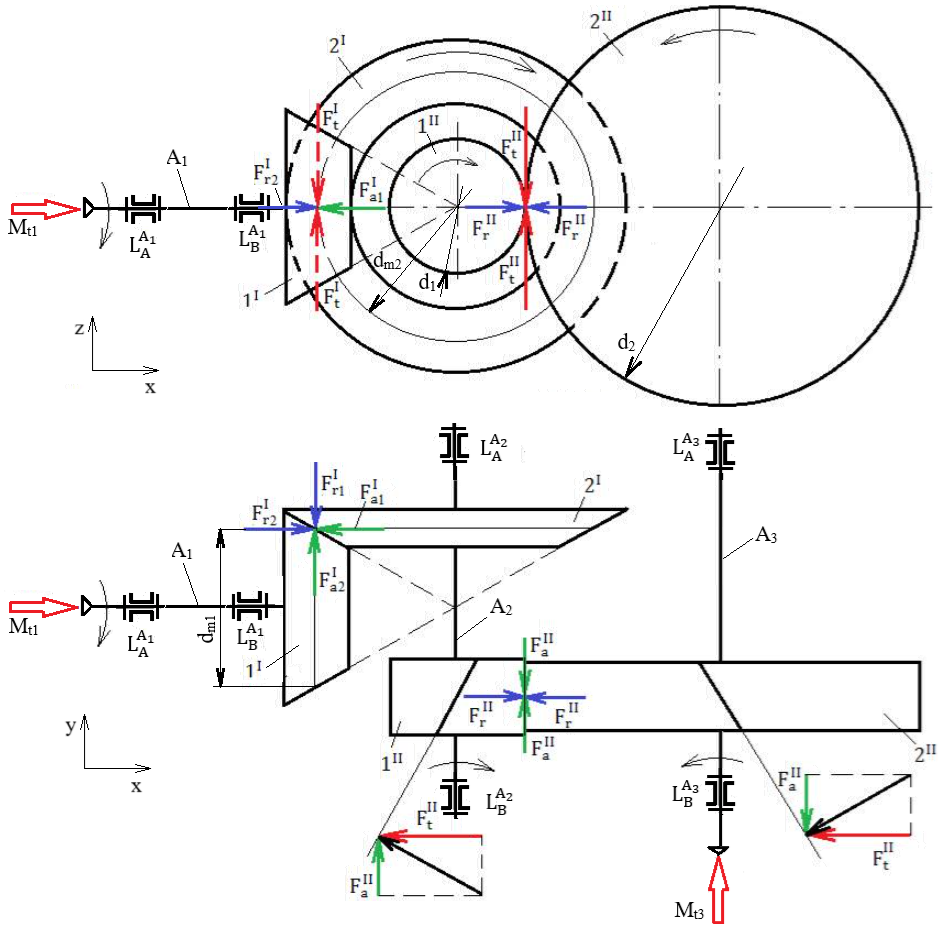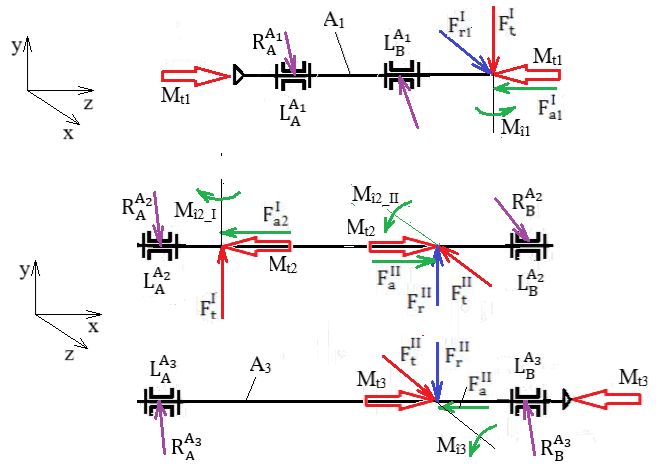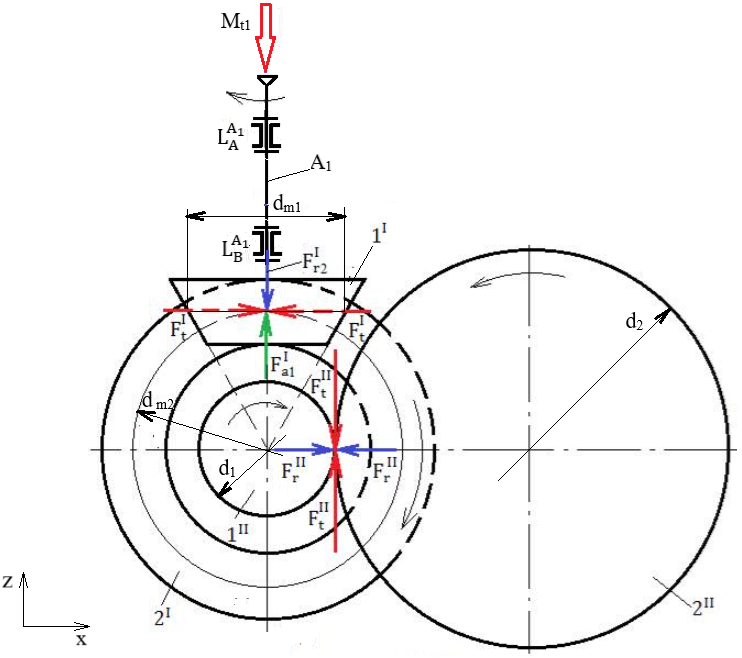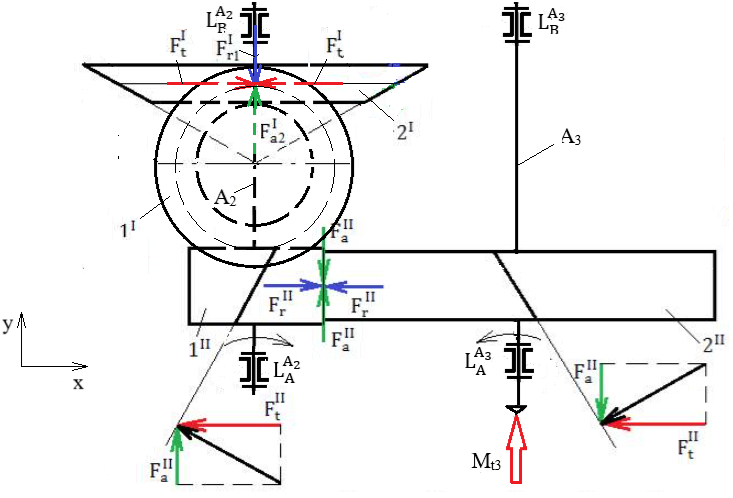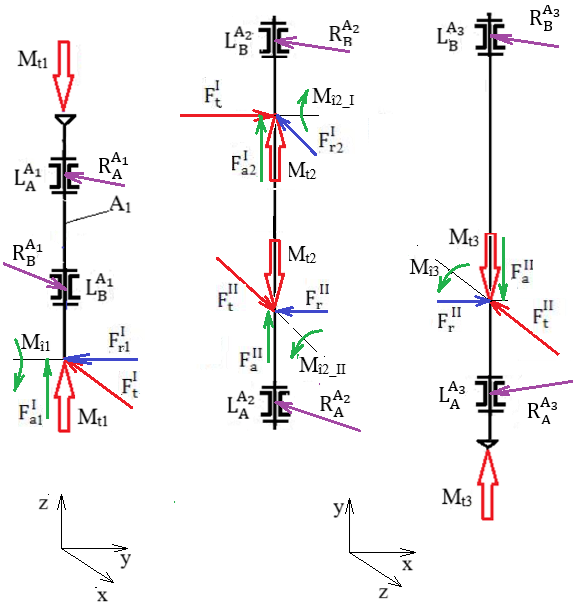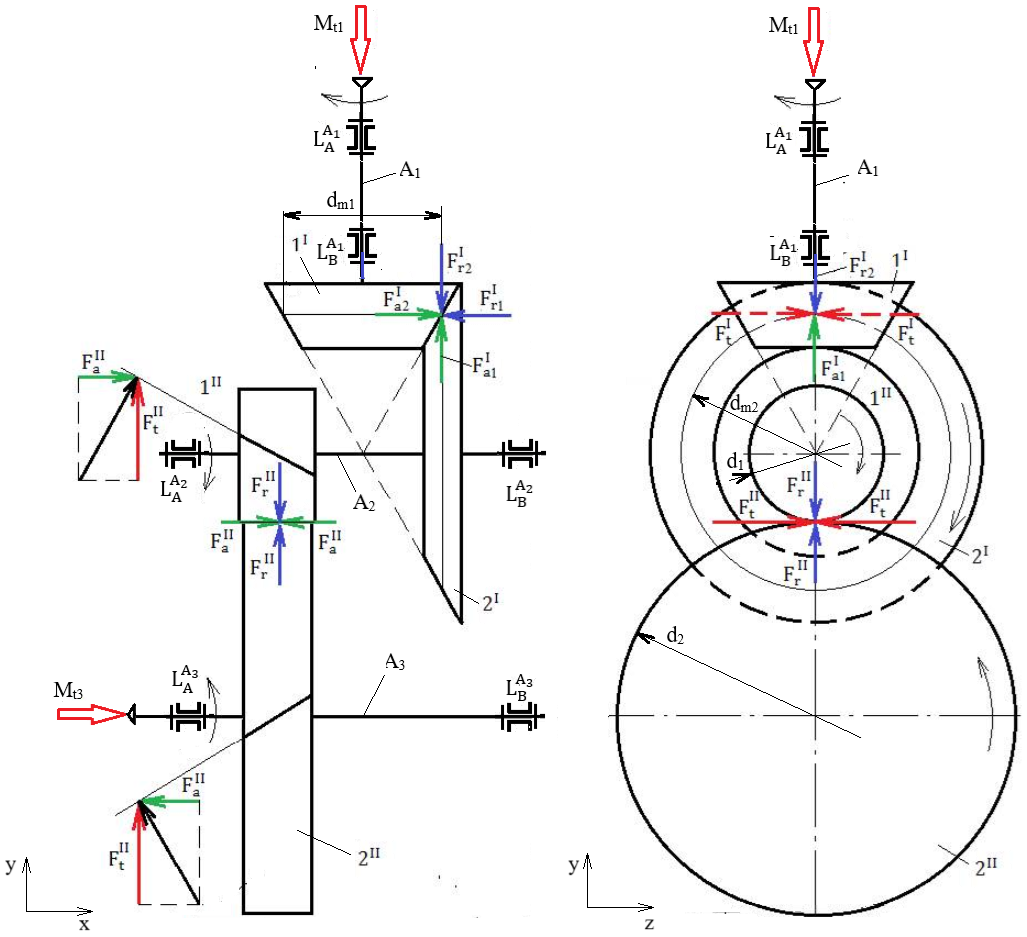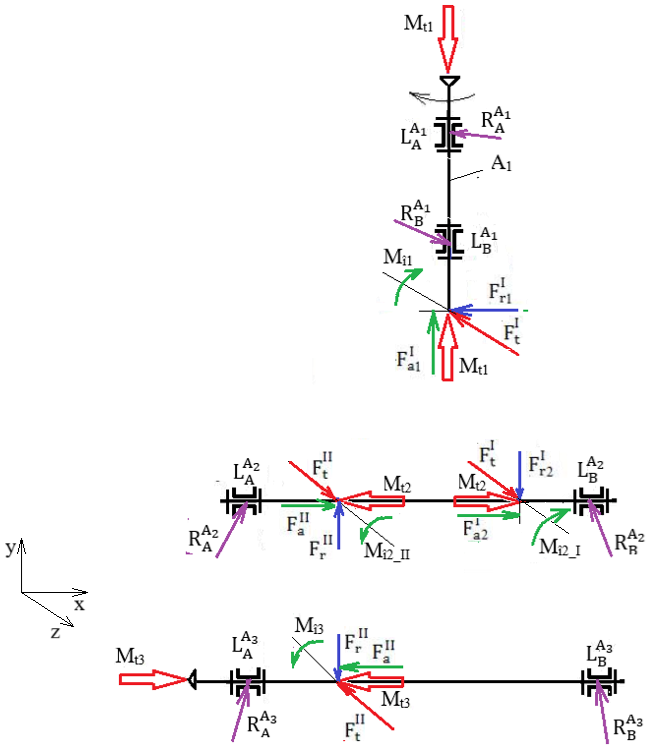Forțele de încărcare a arborilor reductoarelor conico-cilindrice Forțele de încărcare a arborilor unui reductor conico-cilindric HH Semnificații parametrii: I – angrenaj conic, II – angrenaj cilindric,  1^I – pinion conic, 2^I – roată conică,  1^II – pinion cilindric, 2^II – roată cilindrică,  A1 – arbore de intrare, A2 – arbore  intermediar,  A3 – arbore de ieșire,   – lagărul (rulmentul) A al arborelui A1,  – lagărul (rulmentul) B al arborelui A1, – lagărul (rulmentul) A al arborelui A2,  – lagărul (rulmentul) B al arborelui A2, – lagărul (rulmentul) A al arborelui A3,  – lagărul (rulmentul) B al arborelui A3,   [N] – forța tangențială din angrenajul II (conic),   Fr1^I [N] – forța radială a pinionului conic, Fa1^I [N] – forța axială a pinionului conic; Fr2^I [N] – forța radială a roții conice (Fr2^I= Fa1^I), Fa2 [N] – forța axială a roții conice (Fa2^I= Fr1^I), [N] – forța tangențială din angrenajul II (cilindric), [N] – forța radială din angrenajul II (cilindric), [N] – forța axială din angrenajul II (cilindric), Mt1 [Nmm] – momentul de torsiune al arborelui de intrare, Mt2 [Nmm] – momentul de torsiune al arborelui intermediar, Mt3 [Nmm] – momentul de torsiune al arborelui de ieșire, Mî1 [Nmm] – momentul de încovoiere al pinionului conic, Mî2_I [Nmm] – momentul de încovoiere al roții conice, Mî1_II [Nmm] – momentul de încovoiere al pinionului cilindric, Mî3 [Nmm] – momentul de încovoiere al roții cilindrice,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A1,  [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A1,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A2, [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A2,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A3, [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A3, dm1 [mm] – diametrul de divizare mediu al pinionului conic, dm2 [mm] – diametrul de divizare mediu al roții conice, d1 [mm] – diametrul de divizare al pinionului cilindric, d2 [mm] – diametrul de divizare al roții cilindrice. Valorile momentelor de încovoiere: Mî1 =  Fa1^I dm1/2;  Mî2_I =  Fa2^I dm2/2;  Mî2_II =  d1/2;  Mî3 =   d2/2. 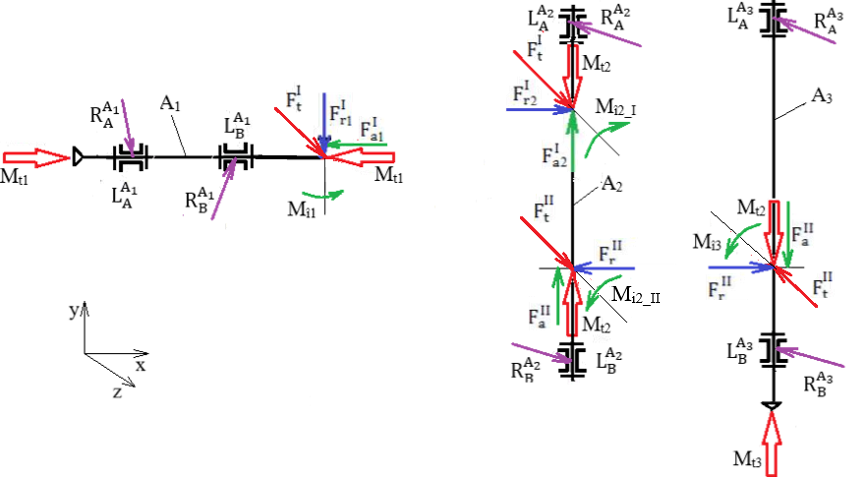Forțele de încărcare a arborilor unui reductor conico-cilindric HV      Semnificații parametrii: I – angrenaj conic, II – angrenaj cilindric,  1^I – pinion conic, 2^I – roată conică,  1^II – pinion cilindric, 2^II – roată cilindrică,  A1 – arbore de intrare, A2 – arbore  intermediar,  A3 – arbore de ieșire,   – lagărul (rulmentul) A al arborelui A1,  – lagărul (rulmentul) B al arborelui A1, – lagărul (rulmentul) A al arborelui A2,  – lagărul (rulmentul) B al arborelui A2, – lagărul (rulmentul) A al arborelui A3,  – lagărul (rulmentul) B al arborelui A3,   [N] – forța tangențială din angrenajul II (conic),   Fr1^I [N] – forța radială a pinionului conic, Fa1^I [N] – forța axială a pinionului conic; Fr2^I [N] – forța radială a roții conice (Fr2^I = Fa1^I), Fa2 [N] – forța axială a roții conice (Fa2^I= Fr1^I), [N] – forța tangențială din angrenajul II (cilindric), [N] – forța radială din angrenajul II (cilindric), [N] – forța axială din angrenajul II (cilindric), Mt1 [Nmm] – momentul de torsiune al arborelui de intrare, Mt2 [Nmm] – momentul de torsiune al arborelui intermediar, Mt3 [Nmm] – momentul de torsiune al arborelui de ieșire, Mî1 [Nmm] – momentul de încovoiere al pinionului conic, Mî2_I [Nmm] – momentul de încovoiere al roții conice, Mî1_II [Nmm] – momentul de încovoiere al pinionului cilindric, Mî3 [Nmm] – momentul de încovoiere al roții cilindrice,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A1,  [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A1,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A2, [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A2,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A3, [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A3, dm1 [mm] – diametrul de divizare mediu al pinionului conic, dm2 [mm] – diametrul de divizare mediu al roții conice, d1 [mm] – diametrul de divizare al pinionului cilindric, d2 [mm] – diametrul de divizare al roții cilindrice. Valorile momentelor de încovoiere: Mî1 =  Fa1^I dm1/2;  Mî2_I =  Fa2^I dm2/2;  Mî2_II =  d1/2;  Mî3 =   d2/2. 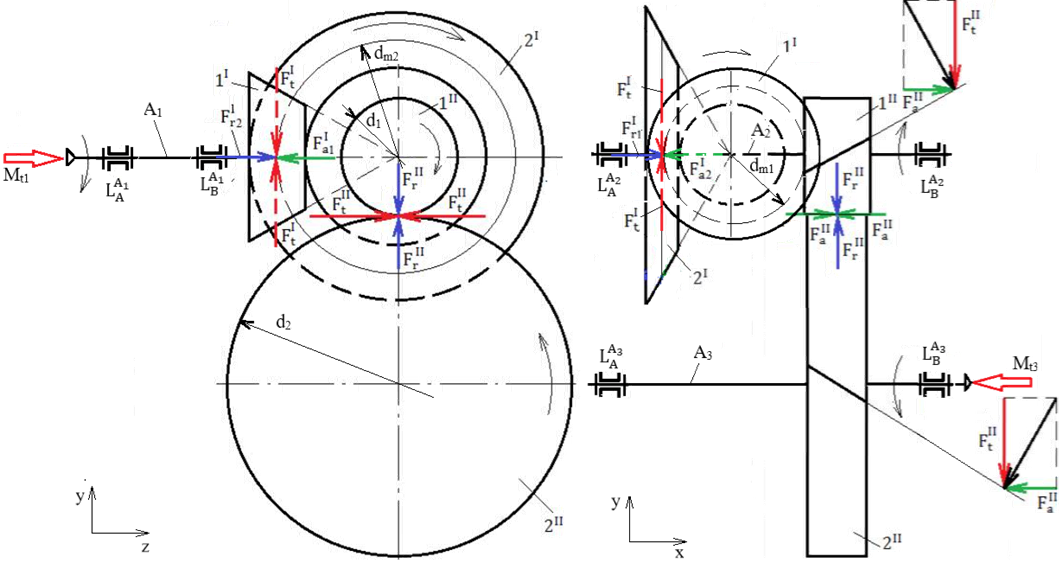Forțele de încărcare a arborilor unui reductor conico-cilindric VH         Semnificații parametrii: I – angrenaj conic, II – angrenaj cilindric,  1^I – pinion conic, 2^I – roată conică,  1^II – pinion cilindric, 2^II – roată cilindrică,  A1 – arbore de intrare, A2 – arbore  intermediar,  A3 – arbore de ieșire,   – lagărul (rulmentul) A al arborelui A1,  – lagărul (rulmentul) B al arborelui A1, – lagărul (rulmentul) A al arborelui A2,  – lagărul (rulmentul) B al arborelui A2, – lagărul (rulmentul) A al arborelui A3,  – lagărul (rulmentul) B al arborelui A3,   [N] – forța tangențială din angrenajul II (conic),   Fr1^I [N] – forța radială a pinionului conic, Fa1^I [N] – forța axială a pinionului conic; Fr2^I [N] – forța radială a roții conice (Fr2^I= Fa1^I), Fa2^I [N] – forța axială a roții conice (Fa2^I= Fr1^I), [N] – forța tangențială din angrenajul II (cilindric), [N] – forța radială din angrenajul II (cilindric), [N] – forța axială din angrenajul II (cilindric), Mt1 [Nmm] – momentul de torsiune al arborelui de intrare, Mt2 [Nmm] – momentul de torsiune al arborelui intermediar, Mt3 [Nmm] – momentul de torsiune al arborelui de ieșire, Mî1 [Nmm] – momentul de încovoiere al pinionului conic, Mî2_I [Nmm] – momentul de încovoiere al roții conice, Mî1_II [Nmm] – momentul de încovoiere al pinionului cilindric, Mî3 [Nmm] – momentul de încovoiere al roții cilindrice,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A1,  [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A1,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A2, [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A2,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A3, [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A3, dm1 [mm] – diametrul de divizare mediu al pinionului conic, dm2 [mm] – diametrul de divizare mediu al roții conice, d1 [mm] – diametrul de divizare al pinionului cilindric, d2 [mm] – diametrul de divizare al roții cilindrice. Valorile momentelor de încovoiere: Mî1 =  Fa1^I dm1/2;  Mî2_I =  Fa2^I dm2/2;  Mî2_II =  d1/2;  Mî3 =   d2/2. Forțele de încărcare a arborilor unui reductor conico-cilindric VV  Semnificații parametrii: I – angrenaj conic, II – angrenaj cilindric,  1^I – pinion conic, 2^I – roată conică,  1^II – pinion cilindric, 2^II – roată cilindrică,  A1 – arbore de intrare, A2 – arbore  intermediar,  A3 – arbore de ieșire,   – lagărul (rulmentul) A al arborelui A1,  – lagărul (rulmentul) B al arborelui A1, – lagărul (rulmentul) A al arborelui A2,  – lagărul (rulmentul) B al arborelui A2, – lagărul (rulmentul) A al arborelui A3,  – lagărul (rulmentul) B al arborelui A3,   [N] – forța tangențială din angrenajul II (conic),   Fr1^I [N] – forța radială a pinionului conic, Fa1^I [N] – forța axială a pinionului conic; Fr2^I [N] – forța radială a roții conice (Fr2^I= Fa1^I), Fa2^I [N] – forța axială a roții conice (Fa2^I= Fr1^I), [N] – forța tangențială din angrenajul II (cilindric), [N] – forța radială din angrenajul II (cilindric), [N] – forța axială din angrenajul II (cilindric), Mt1 [Nmm] – momentul de torsiune al arborelui de intrare, Mt2 [Nmm] – momentul de torsiune al arborelui intermediar, Mt3 [Nmm] – momentul de torsiune al arborelui de ieșire, Mî1 [Nmm] – momentul de încovoiere al pinionului conic, Mî2_I [Nmm] – momentul de încovoiere al roții conice, Mî1_II [Nmm] – momentul de încovoiere al pinionului cilindric, Mî3 [Nmm] – momentul de încovoiere al roții cilindrice,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A1,  [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A1,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A2, [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A2,  [N] – forța de reacțiune din lagărul (rulmentul) A al arborelui A3, [N] – forța de reacțiune din lagărul (rulmentul) B al arborelui A3, dm1 [mm] – diametrul de divizare mediu al pinionului conic, dm2 [mm] – diametrul de divizare mediu al roții conice, d1 [mm] – diametrul de divizare al pinionului cilindric, d2 [mm] – diametrul de divizare al roții cilindrice. Valorile momentelor de încovoiere: Mî1 =  Fa1^I dm1/2;  Mî2_I =  Fa2^I dm2/2;  Mî2_II =  d1/2;  Mî1 =   d2/2
C2.  Fluxuri de forțe în reductoare
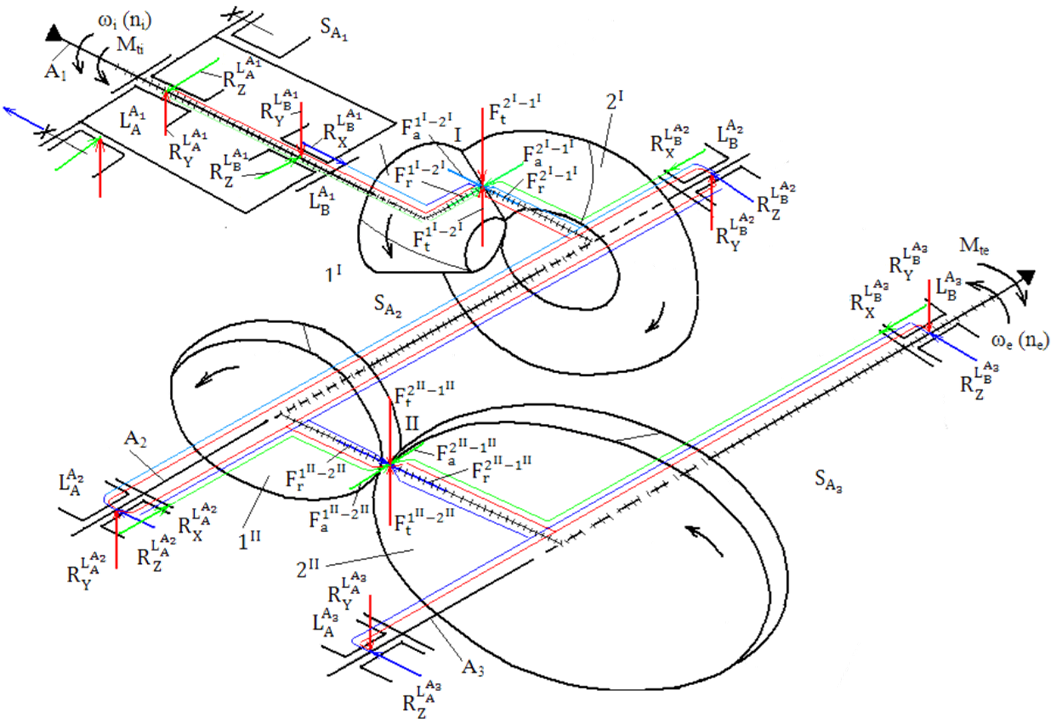
Fluxurile forțelor în reductoarele conico-cilindrice