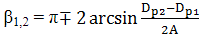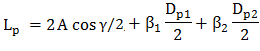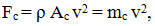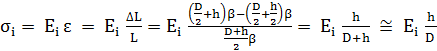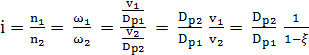TCR. TRANSMISII PRIN CURELE

TCR-T. CONSTRUCŢIA ŞI MODELAREA TRANSMISIILOR PRIN CURELE

CUPRINS

TCR-T.1 DEFINIRE

TCR-T.2 STRUCTURA CONSTRUCTIVĂ

TCR-T.3 DOMENII DE UTILIZARE, AVANTAJE ŞI DEZAVANTAJE

TCR-T.4 CLASIFICARE

TCR-T.5 MATERIALE ŞI TEHNOLOGII

TCR-T.6 FORME ŞI CAUZE DE SCOATERE DIN UZ SAU DE COMPORTARE NECORESPUNZĂTORE

TCR-T.7 PARMETRI FUNCŢIONALI ŞI CONSTRUCTIVI

TCR-T.7.1 Curele trapezoidale înguste

TCR-T.8 MODELE DE CALCUL

TCR-T.8.1 Model de calcul a transmisiilor prin curele trapezoidale înguste

TCR-T.8 MODELE DE CALCUL

TCR-T.8.1 Model de calcul a transmisiilor prin curele trapezoidale înguste fără rolă de întindere

Tab. TCR-T.8.1.1 Relaţii de calcul ale parametrilor de proiectare [STAS 1163]

Relaţii de calcul a parametrilor geometrici (fig. TCR-T.7.1.2)
Unghiul ramurilor curelei		(TCR-T.8.1.1)
Unghiurile de înfăşurare a curelei pe roţi	sau, aproximativ,	(TCR-T.8.1.2)
Lungimea curelei		(TCR-T.8.1.3)
		(TCR-T.8.1.4)
		(TCR-T.8.1.5)
Distanţa dintre axe		(TCR-T.8.1.6)
Relaţii de calcul ai parametrilor funcţionali şi constructivi
Numărul teoretic necesar de curele		(TCR-T.8.1.7)
Viteza periferică (teoretică) a curelei		(TCR-T.8.1.8)
Frecvenţa încovoierilor curelei	f = max (n₁, n₂)	(TCR-T.8.1.9)
Obs. Valorile parametrilor z_max, v_max şi f_max sunt definite de producătorii de curele

Tab. TCR-T.8.1.2 Model de calcul a forţelor

a b

d e

f g

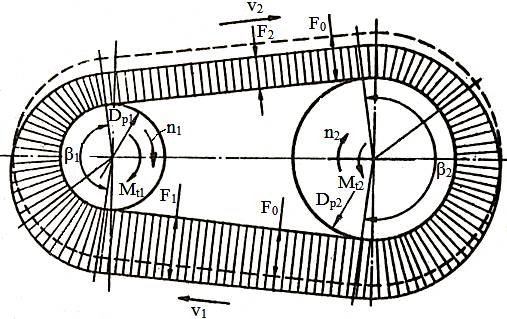
h i

Fig. TCR-T.8.1.1 Forţe în transmisia prin curele: a – încărcarea ramurilor curelei fără sarcină exterioară; b - încărcarea ramurilor curelei sub sarcina exterioară; c – schema de încărcare a curelei; d – schema de calcul a forţei din curea generată de mişcarea de rotaţie (forţa centrifugă); e – schema de calcul a forţei de încărcare a arborelui conducător; f, g, h, i – schema de calcul a forţelor din ramurile curelei

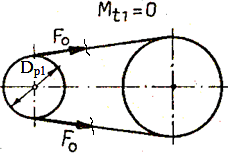
Condiţia de funcţionare: Transmiterea momentului de torsiune prin frecare de la roata conducătoare la curea şi respectiv de la curea la roata condusă presupune existenţa frecării fără alunecare între roţi şi curea şi, implicit, necesită apăsarea (tensionarea) curelei pe roţi.

Ipoteze:

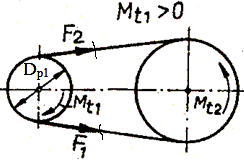
- Apăsarea generată de tensionarea curelei în cazul în care transmisia nu este încărcată cu sarcină exterioară (M_t1 = 0) produce încărcarea curelei cu forţa de tensionare F₀; în cazul transmisiei încărcată cu momentul M_t1 > 0 în ramurile curelei (activă şi pasivă) apar forţele F₁ şi, respectiv, F₂(F₁ > F₂).

- Lungimea totală a curelei fiind independentă de sarcină se poate considera că alungirea ramurii active a curelei cauzată de creşterea efortului cu F₁- F₀ este egală cu scurtarea ramurii pasive cauzată de scăderea efortului F₀-F₂; considerând că modulul de elasticitate al materialului curelei constant, din condiţia de egalitate a deformaţiilor elastice de alungire şi scurtare a curelei rezultă,

F₁- F₀ = F₀-F_2; F₁+ F₂ = 2 F₀. (TCR-T.8.1.10)

- Coeficientul de frecare în zonele de contact ale curelei cu roţile se consideră constant.

Forţe în transmisia prin curele:

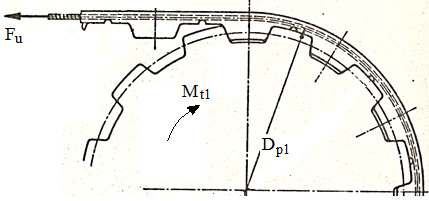
Din ecuaţia de echilibru a roţii conductoare (fig. TCR-T.8.1.1, b,c) rezultă,

(TCR-T.8.1.11)

unde F_u este forţa utilă transmisă de curea, F₁ – forţa din ramura activă (motoare), F₂ – forţa din ramura pasivă (liberă); D_p1– diametrul primitiv al roţii conducătoare.

Din relaţiile (TCR-T.8.1.10) şi (TCR-T.8.1.11) rezultă,

(TCR-T.8.1.12)

(TCR-T.8.1.13)

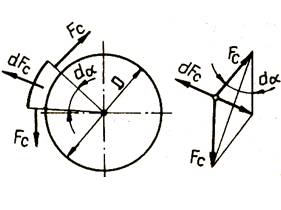
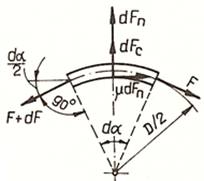
Forţa centrifugă cauzată de mişcarea de rotaţie a elementului de curea înfăşurat pe roată (fig. TCR-T.8.1.1,d) se poate calcula cu relaţia,

, (TCR-T.8.1.14)

în care, ρ este densitatea materialului curelei, v – viteza curelei, A_c - aria secţiunii curelei. Forţa centrifugă dF_c determină în cele două secţiuni ale elementului de curea (fig. TCR-T.8.1.1,d) forţa F_c care solicită suplimentar cureaua la întindere. Pe de altă parte, din condiţia de echilibru în direcţie radială a elementului de curea (fig. TCR-T.8.1.1,d),

. (TCR-T.8.1.15)

Din relaţiile (TCR-T.8.1.14) şi (TCR-T.8.1.15) rezultă relaţia,

(TCR-T.8.1.16)

unde, m_c este masa specifică (pe unitatea de lungime) a curelei.

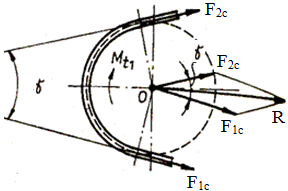
Forţa de încărcare a arborelui la funcţionarea transmisiei sub sarcină (fig. TCR-T.8.1.1,d) se determină cu relaţia,

(TCR-T.8.1.17)

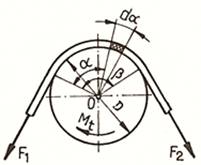
în care, F_1c = F₁ + F_c şi respectiv F_2c = F₂ + F_c; γ - unghiul ramurilor curelei.

Forţele din ramurile curelei se determină din ecuaţiile de echilibru ale elementului de curea (fig. TCR-T.8.1.1,f,g), în direcţiile radială şi tangenţială:

, (TCR-T.8.1.18)

, (TCR-T.8.1.19)

Luând în considerarea aproximările , şi din relaţiile (TCR-T.8.1.18) şi (TCR-T.8.1.19) se obţine,

(TCR-T.8.1.20)

Înlocuind relaţia (TCR-T.8.1.15) în relaţia (TCR-T.8.1.20) se obţine

. (TCR-T.8.1.21)

Prin integrarea acestei ecuaţii,

(TCR-T.8.1.22)

se obţine, relaţia lui Euler,

; . (TCR-T.8.1.23)

Pe baza relaţiilor (TCR-T.8.1.11) şi (TCR-T.8.1.23) se determină expresiile forţelor din ramurile curelei,

; . (TCR-T.8.1.24)

în care F_u este forţa utilă transmisă de curea din relaţia (TCR-T.8.1.11) şi F_c– forţa din curea generată de forţele centrifuge din relaţia (TCR-T.8.1.16).

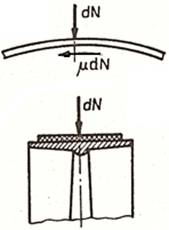
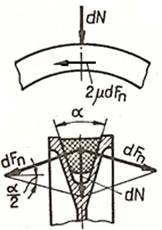
Obs.

a. Coeficientul de frecare utilizat în relaţiile de mai sus corespunde transmisiei prin curele late (fig. TCR-T.8.1.1,h).

b. La transmisiile prin curele trapezoidale, datorită formei trapezoidale a secţiunii curelei (fig. TCR-T.8.1.1,i), apare efectul de pană care conduce la creşterea frecării; astfel din relaţia forţei de frecare (fig. TCR-T.8.1.1,i),

, (TCR-T.8.1.25)

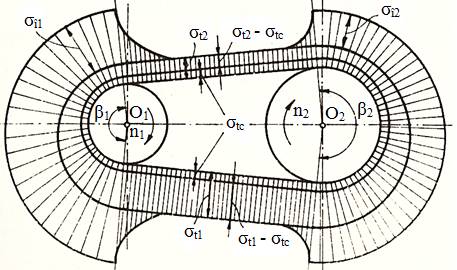
se obţine, coeficientul de frecare redus dintre cureaua trapezoidală şi roata de curea. Pentru a se evita înţepenirea curelei în canalul de pană unghiul

curelei α 34^o; pentru α = 40^o, valoarea standard pentru curelele trapezoidale, se obţine care evidenţiază o capacitate de transmitere a momentului mult mărită; consecinţă a frecărilor mărite din transmisia prin curele trapezoidale aderenţa curelei la roată este mărită şi deci unghiul de înfăşurare minim a curelei trapezoidale pe roată β_min = 110^o, faţă de β_min = 150^o unghiul de înfăşurare minim pentru cureaua lată.

Tab. TCR-T.8.1.3 Model de calcul a tensiunilor

Fig. TCR-T.8.1.2 Tensiunile din curea: a – schema de calcul a tensiunilor de încovoiere; b – schema tensiunilor sub sarcină

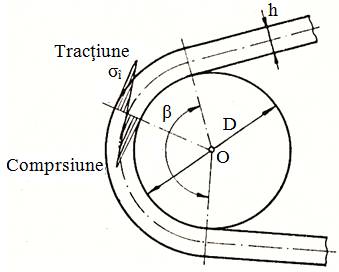
Ipoteze:

- înfăşuraea curelei cauzează tensiuni suplimentare de încovoiere în secţiunea curelei care se consideră distribuite liniar în secţiunea curelei considerând fibra media la h/2 (fig. TCR-T.8.1.2,a);

- valoarea maximă a tensiunii de încovoiere apare la înfăşurarea curelei pe diametrul roţii mici.

Tensiunea de încovoiere în curea în zonele de înfăşurare pe roată (fig. TCR-T.8.1.2,a):

, (TCR-T.8.1.26)

unde E_i este modulul de elasticitate la încovoiere al materialului curelei, ε – deformaţia (alungirea) specifică, ΔL – alungirea fibrei exterioare a curelei, L – lungimea porţiunii de curea înfăşurată pe roată, D – diametrul minim de înfăşurare a curelei, h – înălţimea curelei, β – unghiul de înfăşurare a curelei.

Tensiuni în curea sub sarcină:

Tensiunile de întindere din curea, generate de forţele F₁ şi F₂ care încarcă ramurile curelei, ţinând cont de relaţiile (TCR-T.8.1.24):

, (TCR-T.8.1.27)

, (TCR-T.8.1.28)

sau ţinând cont de relaţiile (TCR-T.8.1.12) şi (TCR-T.8.1.13),

, (TCR-T.8.1.28)

în care, σ_tu este tensiunea utilă generată de forţa utilă F_u (TCR-T.8.1.11), σ_tc – tensiunea generată de forţa F_c (TCR-T.8.1.16), σ_t0 – tensiuna determinată de forţa de tensionare, F₀.

Tensiunea maximă din curea în zona de trecere de la ramura activă la zona de înfăşurare pe roata mică (fig. TCR-T.8.1.2,b), ţinând cont de relaţia (TCR-T.8.1.26), este

. (TCR-T.8.1.29)

sau, ţinând cont de relaţiile (TCR-T.8.1.28)

(TCR-T.8.1.30)

Obs.

a. În practică se recomandă utilizarea curelelor cu înălţime h mică a secţiunii care au tensiunea de încovoiere redusă (TCR-T.8.1.25)

b. Din relaţia (TCR-T.8.1.30) se observă că pentru o valoare limtată a tensiunii maxime σ_max capacitatea de transmitere a momentului de torsiune de către curea, proporţională cu tensiunea σ_tu, este diminuată de tensiunea determinată de forţa de pretensionare, tensiunea de încovoiere şi de tensiunea determinată de forţa centrifugă.

Tab. TCR-T.8.1.4 Model de calcul cinetostatic

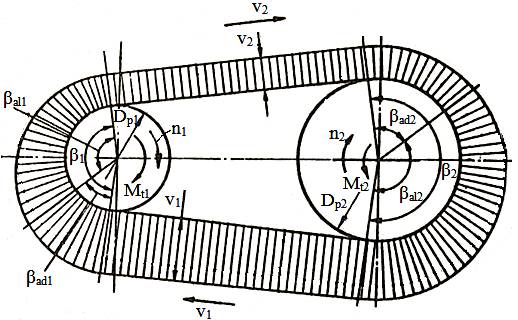
Fig. TCR-T.8.1.3 Schema de calcul a alunecării specifice

Fig. TCR-T.8.1.4 Curbele (caracteristicile) de alunecare ale curelei

Ipoteze:

- forţele diferite din ramurile curelei – F₁ din ramura activă şi F₂ din cea pasivă – determină deformaţii diferite ale curelei, mai mari în ramura activă şi mai mici în ramura pasivă;

- din cauza deformaţiilor elastice diferite la trecerea curelei peste roata conducătoare aceasta trebuie să ajungă de la o alungire mai mare la una mai mică şi deci cureaua se contractă, punctele de pe curea deplasându-se cu o viteză mai mică decât punctele corespunzătoare de pe roată şi cureaua pe o zonă unghiulară β_al1 (fig. TCR-T.8.1.3) se deplasează mai încet faţă de roată, producându-se o alunecare (patinare), şi în zona unghiulară β_ad1 = β₁ - β_al1 rămânând în contact fără alunecare (aderenţă);

- din cauza deformaţiilor elastice diferite la trecerea curelei peste roata condusă aceasta trebuie să ajungă de la o alungire mai mică la una mai mare şi deci cureaua se alungeşte, punctele de pe curea deplasându-se cu o viteză mai mare decât punctele corespunzătoare de pe roată şi cureaua pe o zonă unghiulară β_al2 (fig. TCR-T.8.1.3) se deplasează mai repede faţă de roată, producându-se o alunecare (patinare), şi în zona unghiulară β_ad2 = β₂ - β_al2 rămânând în contact fără alunecare (aderenţă);

- consecinţă a alungirilor diferite ale curelei pe cele două ramuri, vitezele deplasare în aceste zone sunt v₁, pentru ramura activă şi v_2,pentru ramura pasivă.

Alunecarea specifică

Mişcorarea vitezei punctelor curelei de pe ramura activă de la v₁la v₂ pentru punctele ramurii pasive (fig. TCR-T.8.1.3) din cauza deformaţiilor elastice se exprimă prin coeficientul de alunecare elastică,

, (TCR-T.8.1.31)

care, conform ipotezelor de mai sus, considerând ramura curelei o bară solicitată la tracţiune se determină cu relaţia,

, (TCR-T.8.1.32)

în care, ε₁ este deformaţia ramurii active, ε₂ - deformaţia ramurii pasive, E – modulul de elasticitate longitudinal al materialului curelei, A_c – aria secţiunii curelei.

Din relaţia (TCR-T.8.1.31) rezultă expresia raportului de transmitere,

, (TCR-T.8.1.33)

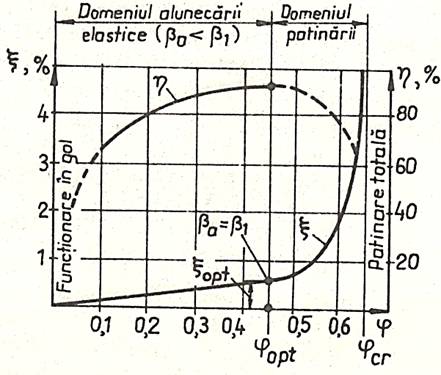
în care n_1,2 sunt turaţiile roţilor, D_p1,2 – diamterele primitive.

Curbele (cracteristile) de alunecare ale curelei

În urma cercetărilor experimentale a curelelor realizate din materiale diferite s-au stabilit dependenţele între coeficientul de alunecare elastică ξ, randamentul η şi coeficientul de tracţiune φ = F_u/2F₀ (fig. TCR-T.8.1.4); aceste curbe se folosesc pentru calculul de dimensionare a transmisei pe baza punctului optim de funcţionare cu β₁ = β_al (β_ad1 = 0) şi φ = φ_opt, determinate experimental pentru fiecare tip de curea.

Obs.

a. Mărimea unghiului de alunecare/patinare β_al1 depinde de forţa utilă F_u; dacă aceasta creşte unghiul de alunecare/patinare creşte (unghiul de adeziune β_ad1 (fig. TCR-T.8.1.3) scade); în cazul în care β_al = β₁ (β_ad1 = 0), unghiul de contact al curelei cu roata, transmisia utilizează întreaga capacitate portantă a curelei şi deci forţa F_ueste maximă; la valori mai mari ale acestei forţe (consecinţă a supraîncărcării transmisiei) se produce fenomenul de patinare totală a curelei pe roată.

b. Raportul de transmitere (TCR-T.8.1.33) nu este constant, depinde de încărcarea transmisiei prin coeficientul de alunecare (TCR-T.8.1.32).

c. Interpretarea curbelor de alunecare din fig. TCR-T.8.1.4:

- la φ = 0, transmisia funcţionează în gol;

- pentru 0< φ < φ_opt, există patinare în zona, β_al < β₁, şi creşte randamentul;

- la φ = φ_opt, există patinare pe toată zona de înfăşurare, β_al = β₁, utilizează complet capacitatea portantă a curelei şi randamentul este maxim, η_max = 0,95…0,98 (de ex. φ_opt = 0,59 pentru curelele late din piele, φ_opt = 1 pentru curelele trapezoidale);

- pentru φ_opt < φ se produce patinarea curelei pe roată, proces nedorit în funcţionare.

TCR-T.8.2 Model de calcul a transmisiilor prin curele dinţate

Tab. TCR-T.8.2.1 Model de calcul geometric (Fig. TCR-T.7.2.2)

Unghiul ramurilor curelei		(TCR-T.8.2.1)
Unghiurile de înfăşurare a curelei pe roţi		(TCR-T.8.2.2)
Lungimea curelei		(TCR-T.8.2.3)
		(TCR-T.8.2.4)
		(TCR-T.8.2.5)
Distanţa dintre axe		(TCR-T.8.2.6)
Numărul mediu de dinţi (activi) în contact cu roata 1, respectiv 2		(TCR-T.8.2.7)

Tab. TCR-T.8.2.1 Modele de calcul a eforturilor şi tensiunilor

Fig. TCR-T.8.2.1 Eforturi şi tensiuni în curea: a – schema forţei utile; b – schema tensiunilor sub sarcină

Eforturi în cureua dinţată

Din relaţia (TCR-T.8.1.11), considerând F₂ = 0, rezultă forţa din ramura activă,

(TCR-T.8.2.8)

Forţa de încărcare a arborelui la funcţionarea transmisiei sub sarcină se obţine din relaţia (TCR-T.8.1.17) considerând F_1c = F₁ + F_c şi F_2c = F_c (pentru F_c, v. rel. (TCR-T.8.1.16)),

. (TCR-T.8.2.9)

Tensiuni în curea:

Tensiunea de tracţiune din secţiunea structurii de rezistenţă, ţinând cont de relaţia (TCR-T.8.1.16), este,

. (TCR-T.8.2.10)

unde, este aria secţiunii de rezistenţă cu n numărul cablurilor (firelor) cu diametrul d.

Tensiunea de încovoiere, la înfăşurarea curelei pe roţi analog relaţiei relaţiei (TCR-T.8.1.25),

, (TCR-T.8.2.11)

unde k_i E < < E; aceste tensiuni au valori mici;

Tensiunea maximă din curea (fig. TCR-T.8.1.2) se determină cu relaţia,

σ_max = σ_tu + σ_tc+ σ_î1. (TCR-T.8.2.12)

Tensiuni în dinţii curelei:

Tensiunea maximă de încovoiere a dintelui (fig. TCR-T.8.2.1,b),

. (TCR-T.8.2.13)

Tensiunea de strivire pe flancul dintelui (fig. TCR-T.8.2.1,b),

. (TCR-T.8.2.14)

Tensiunea de forfecare a dintelui (fig. TCR-T.8.2.1,b),

. (TCR-T.8.2.15)

Obs. Valorile tensiunilor admisible la încovoiere, la strivitre şi la forfecare, σ_aî ,σ_as, şi respectivτ_af corespund materialului curelei

TCR-T.9 SISTEME DE TENSIONARE (ÎNTINDERE) A CURELELOR

Scop: Realizarea presiunilor de contact dintre curea şi roţile de curea şi implicit a forţelor de frecare necesare transmiterii sarcinii exterioare.

TCR-T.9.1 Sisteme de tensionare permanentă

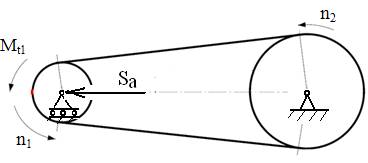
Tensionarea permanentă poate fi realizată prin aplicarea unei forţe de întindere S_a asupra unei roţi (fig. TCR-T.9.1.1,a) sau prin aplicarea unei forţe invariabilă ca intensitate pe una din ramuri (de obicei pe ramura condusă, fig. TCR-T.9.1.1,b,c); tensionarea curelei se poate face la montaj sau în timpul funcţionării.


a	b	c
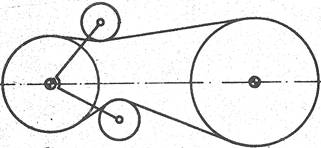
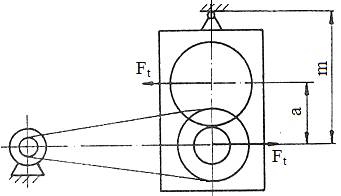
*Fig. TCR-T.9.1.1* Sisteme de tensionare (întindere) permanentă a curelei: a - cu reglarea la montaj a poziţiei unei roţi (de, obicei a celei mici, fer. TCR-S.1.1); b – cu rolă de întindere la exterior; c – cu rolă de întindere la interior [STAS 1163]

TCR-T.9.2 Sisteme de tensionare automată

Tensionarea automată presupune generarea unei forţe de tensionare variabilă în funcţie de momentul rezistent; la funcţionarea în gol sau în repaus tensiunile din ramurile curelei sunt nule, astfel, eliminându-se, dezavantajul principal al sistemelor de tensionare permanentă (asigură tensionarea la valoarea maximă a momentului rezistent). Aceste sisteme asigură funcţionarea transmisiei în zona coeficientului de tracţiune optim φ_optindiferent de sarcina transmisă. Sistemele de tensionare automată au dezavantajul că nu realizează protecţia la suprasarcini a ansamblului transmisiei.

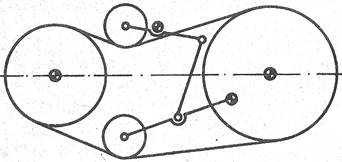
Fig. TCR-T.9.2.1 Sisteme de tensionare (întindere) automată a curelei dependente de sarcina transmisă: a - cu mecanism cu două role de întindere la exterior;

b – cu mecanism cu două role de întindere la exterior şi la interior; c – cu mecanism de întindere prin deplasarea unei roţi