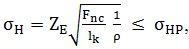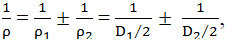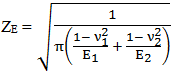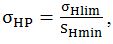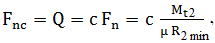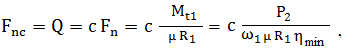TFR. TRANSMISII PRIN FRICŢIUNE
TFR-T.2 TRANSMISII PRIN FRICŢIUNE CU RAPORT DE TRANSMITERE VARIABIL (VARIATOARE)
|
CUPRINS |
|
TFR-T.2.1
DEFINIRE
TFR -T.2.2 STRUCTURI CONSTRUCTIVE
TFR -T.2.3 DOMENII DE UTILIZARE, AVANTAJE ŞI
DEZAVANTAJE
TFR -T.2.4 CLASIFICARE
TFR -T.2.5
MATERIALE ŞI TEHNOLOGII
TFR -T.2.6
FORME ŞI CAUZE DE SCOATERE DIN UZ SAU DE COMPORTARE
NECORESPUNZĂTORE
TFR -T.2.7
PARMETRII FUNCŢIONALI ŞI CONSTRUCTIVI TFR -T.2.8 MODELE DE CALCUL TFR-T.2.8.1 Modele de calcul cinetostatic TFR-T.2.8.1.1 Variatoare frontale cu role TFR-T.2.8.1.2 Variatoare sferice TFR-T.2.8.1.3 Variatoare toroidale TFR-T.2.8.1.4 Variatoare planetare TFR-T.2.8.1.5 Variatoare cu conuri deplasabile şi element (inel) rigid TFR-T.2.8.1.6 Variatoare cu conuri deplasabile şi element flexibil (curea) sau articulat (lanţ) TFR-T.2.8.1.6.1 Variatoare cu conuri deplasabile şi element flexibil (curea) sau articulat (lanţ) prin tragere
TFR-T.2.8.1.6.2
Variatoare cu conuri deplasabile şi
element flexibil metalic prin împingere (Van Doorne)
TFR-T.2.8.2 Model de calcul
la solicitarea de contact |
TFR-T.2.1 DEFINIRE
Transmisiile prin fricţiune transmit mişcarea de rotaţie şi momentul de torsiune, de la un element conducător la unul sau mai multe elemente conduse, prin intermediul forţei de frecare, în timp ce elementele active de tip roată, aflate în contact direct, sunt apăsate reciproc cu o forţă normală cu mărimea suficientă ca să se evite patinarea.
Transmisiile prin fricţiune cu raport de transmitere variabil sunt transmisii mecanice la care mişcarea de rotaţie şi momentul de torsiune se transmite, de la elementul conducător la cel condus la care se obţine o turaţie variabilă continuu între anumite limite ca urmare a posibilităţii de modificare a raportului de transmitere continuu în timpul mişcării.
TFR-T.2.2 STRUCTURI
CONSTRUCTIVE
|
|
|
|
a |
b |
|
Fig.
TFR-T.2.1 Cutie
de viteze automată cu variator de turaţie cu lanţ (http://www.cvt.co.nz) a – vedere
secţionată; b – vedere
lanţ |
|
TRV-T.2.3 DOMENII DE UTILIZARE, AVANTJE ŞI
DEZAVANTAJE
Domenii
principale de utilizare: cutii de
viteze automate (CVT - Continuously Variable
Transmission) ale vehiculelor, maşini agricole, tractoare; utilajelor
tehnologice,
Tab.
TFR-T.3.1 Avantajele şi dezavantajele variatoarelor de turaţie
|
Avantaje* |
Dezavantaje* |
|
- obţinerea unei caracteristici de transmitere a momentului de torsiune constantă; -
funcţionare
la nivel redus de vibraţii
şi zgomote -
asigură
protecţia transmisiei în cazul apariţiei a unor suprasarcini în
funcţionare |
- în cazul unui raport de transmitere fixat, acesta nu se menţine constant în timpul funcţionării ca urmare a alunecărilor (geometrice sau elastice) din zona de contact; - randamentul este mai redus; - uzuri neuniforme ale elementelor în contact; - durabilitate scăzută - necesită forţe mari de apăsare care
încarcă arborii şi lagărele şi deci, gabarite mărite |
|
* raportate la transmisiile cu raport de transmitere
constant (prin roţi dinţate, curele etc.) |
|
TFR-T.2.4 CLASIFICARE
Tab. TFR-T.2.4.1 Clasificarea variatoarelor cu fricţiune
|
Criteriul |
Tipul |
Exemple |
|
|
|
|
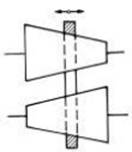
Numărul contactelor |
Mono |
Fig. TRV-T.4.1; TFR-T.2.8.1.1.3, a |
|||
|
Duo |
Fig. TRV -T. 4.2; TFR-T.2.8.1.1.3, b |
||||
|
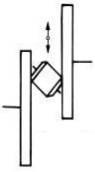
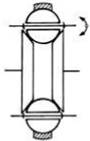
Poziţia/forma elementelor active |
Frontale |
Fig. TRV -T. 4.1,a; TFR-T.2.8.1.1.3 |
|||
|
Conice |
Fig. TRV -T. 4.1,b |
||||
|
Sferice |
Fig. TRV -T. 4.2,d; TFR-T.2.8.1.2.1 |
||||
|
Disc |
TRV -T. 4.2,c |
||||
|
Subsistemul de
generare a forţei de apăsare |
Cu apăsare constantă |
Fig. TFR-T.2.8.1.1.1 |
|||
|
a |
b |
c |
|||
|
Cu apăsare automată |
Fig.
TFR-T.2.8.1.5.1;
TFR-T.2.8.1.4.1 TFR-T.2.8.1.3.1 |
Fig. TFR-T.4.1 Scheme de variatoare mono: a – frontal; b – conic; c – cu disc |
|||
|
|
|
|
|
|
|
|
|
|
a |
b |
c |
d |
e |
f |
g |
h |
|
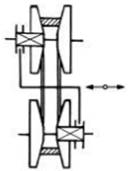
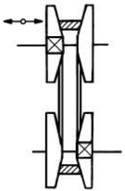
Fig. TFR-T.4.2 Scheme de variatoare duo: a – frontal; b – conic; c – cu role biconice; d – sferic; e – toroidal; f – cu inel metalic; g – cu lanţ; h – prin curele |
|||||||
TFR-T.2.5 MATERIALE
ŞI TEHNOLOGII
Cerinţele
principale pe care
trebuie să le îndeplinească materialele utilizate pentru
construcţia elementelor active ale transmisiilor prin fricţiune sunt:
rezistenţa la solicitarea de contact; rezistenţa la uzură ;
coeficient de frecare cât mai mare – pentru a se evita forţe de
apăsare mari – şi constant în timp.
Cupluri
de materialele metalice caracterizate de rezistenţe ridicate la solicitarea de contact şi
uzură:
-
oţel
călit/ oţel călit – pentru transmisiile puternic încărcate,
la care se cere o durabilitate mare şi care funcţionează cu sau
fără ungere – caracterizate prin gabarit minim ăi randament
ridicat; necesită precizii ridicate de execuţie şi montaj,
concomitent cu reducerea alunecărilor geometrice, care ar putea duce la
apariţia gripării;
-
fontă/
oţel călit – pentru transmisiile care funcţionează cu sau
fără ungere, prezentând avantajul unei rezistenţe sporite la
gripare;
-
fontă/
fontă – pentru transmisiile care
funcţionează cu ungere.
Cupluri de materialele metalice caracterizate prin coeficienţi de frecare mari şi elasticităţi mărite: textolit, cauciuc, piele etc./oţel sau fontă – pentru transmisii puţin încărcate, care funcţionează fără ungere şi se caracterizează prin dimensiuni de gabarit mari şi randament mai scăzut; materialul nemetalic se foloseşte sub formă de căptuşeli, montate pe elementul conducător, pentru asigurarea unei uzuri uniforme.
Uleiuri de tracţiune pentru transmisii prin fricţiune cu raport de transmitere variabil
|
Fig. TFR-T.2.5.1 Schema contactului cu ulei de tracţiune [https://en.wikipedia.org/wiki/Continuously_variable_transmission] |
Uleiul de tracţiune este compus din molecule cu dimensiuni mari şi cu protuberanţe în formă de pană care în condiţiile de contact cu presiuni extrem de ridicate formează o structură de molecule aliniate ordonat şi devine pentru scurt timp foarte vâscos comportându-se aproape ca un corp solid. Spre deosebire de uleiurile de transmisie care rămân tot timpul lichide şi realizează coeficienţi de frecare mici (0,05...0,06) uleiurile de tracţiune prin solidificare în zona de contact generează forţe de frecare mari (coeficienţi de frecare, aprox. 0,1) şi, în plus, se diminuează pătrunderea acestuia în microfisurile suprafeţelor în contact. Uleiul de tracţiune trebuie să asigure şi performanţele de ungere şi răcire la fel ca un ulei de transmisie. Caracteristicile uleiurilor de tracţiune: - coeficient de frecare mărit ce asigură un transfer de putere mărit; - eliminină contactele directe şi asigură funcţionare silenţioasă. - asigură randamente şi performanţe dinamice mărite; - diminuează uzarea prin pitting; - stabilitate la temperaturi ridicate; - proprietăţi de ungere cât mai apropiate de ale uleiurilor de transmisie; - comportament hidraulic cât mai constant într-un domeniu larg de temperaturi (-40...140o) |
TFR-T.2.6 FORME
ŞI CAUZE DE SCOATERE DIN UZ SAU DE COMPORTARE NECORESPUNZĂTOARE
Tab. TFR-T.2.6.1 Forme şi cauze de comportare necorespunzătoare sau de scoatere din uz
|
Forme |
Consecinţe |
Apariţie |
Cauze |
Manifestare |
Evitare |
|
Deteriorarea suprafeţelor elementelor active prin pitting |
Comportare
necorespunzătoare (cu neuniformităţi, vibraţii şi
zgomote) |
Variatoare cu ungere |
Oboseala de contact (pitting) |
Microfisuri şi ciupituri pe suprafaţele
active |
Limitarea tensiunii maxime
de contact la valori admise de cuplul de materiale |
|
Deteriorarea suprafeţelor elementelor active prin gripare |
Comportare
necorespunzătoare (cu neuniformităţi, vibraţii şi
zgomote) |
Varaiatoare
cu ungere |
Griparea |
Creşterea frecărilor, a temperaturilor locale,
apariţia de microsuduri şi zgârieturi pe suprafețele active |
Limitarea vitezei de funcţionare la valori admisibile
|
|
Deteriorarea
suprafeţelor elementelor active |
Comportare necorespunzătoare (cu neuniformităţi, vibraţii şi zgomote) |
Variatoare fără ungere |
Uzarea abrazivă |
Apariţia
de zgârieturi pe suprafețele active |
Ungerea şi etanşarea corespunzătoare |
TFR-T.2.7 PARMETRI
FUNCŢIONALI ŞI CONSTRUCTIVI
|
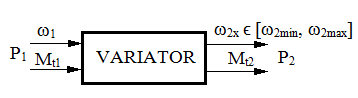
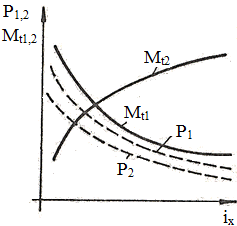
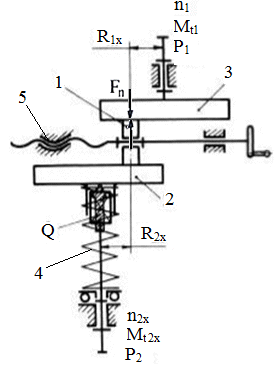
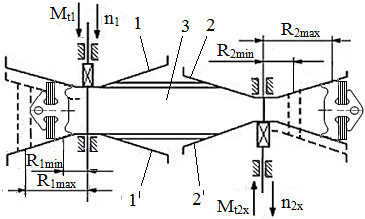
Parametrii care caracterizează cinetostatica unei transmisii prin fricţiune cu raport de transmitere variabil (variator) sunt: vitezele unghiulare sau turaţiile, momentele de torsiune şi puterile de la intrare, respectiv, ieşire (fig. TFR-T.2.7.1,a). Parametrii de intrare: viteza unghiulară ω1 [rad/s] (turaţia n1 [rot/min]); momentul de torsiune Mt1 [Nmm]; puterea P1 [kW]. Parametrii de ieşire: viteza unghiulară ω2x ϵ [ω2min, ω2max] [rad/s] (turaţia n2x ϵ [n2min, n2max] [rot/min]), variabilă; momentul de torsiune Mt2 [Nmm]; puterea P2 [kW]. Raportul de transmitere instantaneu: ix = ω1/ω2x = n1/n2x este variabil, modificabil prin reglarea unor mărimi ale variatorului, şi poate avea valoarea minimă, imin = ω1/ω2max = n1/ n2max sau maximă, imax = ω1/ω2min = n1/ n2min. Gama de reglare se defineşte ca raport al vitezelor unghiulare maximă şi minimă a elementului condus al variatorului,
Variatoarele având viteza unghiulară a elementului condus variabilă, într-un anumit interval, au parametrii care caracterizează mişcarea elementului conducător şi condus dependente de această viteză unghiulară (ω2x) sau de raportul de transmitere (ix). Astfel, considerând viteza unghiulară a elementului conducător ω1 = const. se pot scrie relaţiile:
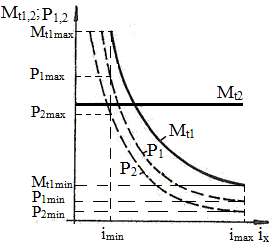
şi admiţând modul de variaţie a uneia dintre mărimi (de ex. Mt1 descrescătoare neliniar) se pot descrie variaţiile din fig. TFR-T.2.5.1,b. În aceaste relaţii s-a considerat ηx, randamentul, dependent de viteza variabilă, deci şi de raportul de transmitere ix. De obicei, în funcţionarea variatoarelor (ω1 = const., ω2x = variab.) în funcţie de destinaţie se pot întâlni două regimuri de funcţionare, care implică menţinerea constantă a unuia dintre parametrii cinetostatici ai elementului condus (Mt2 sau P2): - Mt2 = const. (situaţie frecvent întâlnită în cazul transmisiilor utilizate în construcţia sistemelor de transfer şi transport) , caz ce conduce la relaţiile:
care au formele din fig. TFR-T.2.5.1,c; în acest caz puterea motorului de intrare (antrenare) nu este folosită integral pe tot parcursul de funcţionare şi în regim staţionar se identifică valorile limită (maxime şi minime):
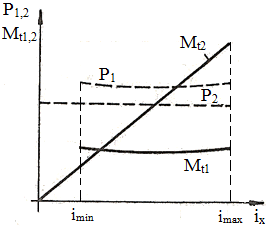
- P2 = const. (situaţie ce impune folosirea integrală a puterii motorului), caz ce conduce la relaţiile:
care au formele din fig. TFR-T.2.5.1,d; în acest caz puterea motorului de intrare (antrenare) variază relativ puţin în raport cu raportule de transmitere instantaneu ix; la majoritatea transmisiilor se poate admite ηx(ix) = const., deci, se poate considera că puterea motorului de antrenare este cvasiconsatantă şi, în consecinţă, şi momentul de torsiune de antrenare (prima relaţie din grupul (TFR-T.2.7.5)) este cvasiconstant. |
|||
|
|
|
|
|
|
a |
b |
c |
d |
|
Fig.
TFR-T.2.7.1
Scheme funcţionale ale variatoarelor: a – schema bloc; b – caracteristicile funcţionale pentru cazul general |
|||
TFR-T.2.8 MODELE DE
CALCUL
TFR-T.2.8.1 Modele de calcul cinetostatic
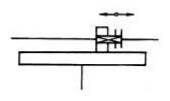
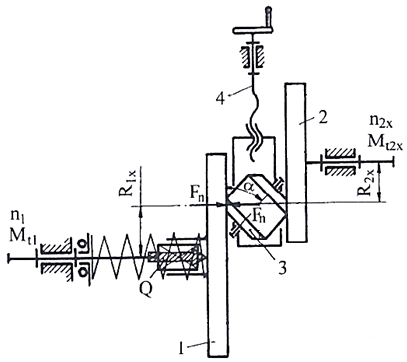
TFR-T.2.8.1.1 Variatoare frontale cu role
|
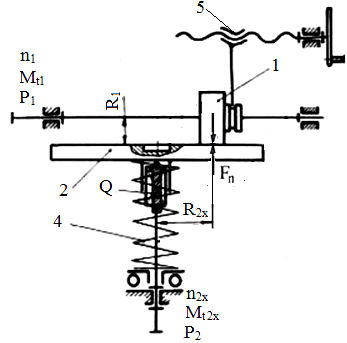
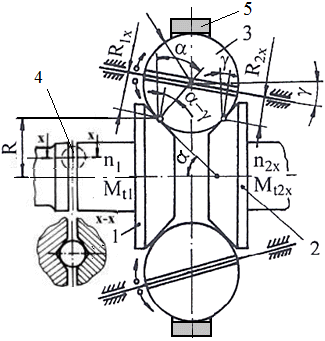
Funcţionare:
Variatorul frontal cu rolă cilindrică,
mono (fig. TRV-T.8.1.1.1,a):
Mişcarea şi momentul de torsiune de la arborele de intrare se
transmit prin canelură la rola cilindrică 1, apoi prin frecare la
discul condus 2. Forţa de apăsare constantă, Q, este
realizată de sistemul cu arc 4. Sistemul de modificare a raportului de
transmitere realizează modificarea turaţiei la ieşire ca urmare
a modificării razei de contact R2x prin
intermediul mecanismului şurub-piuliţă, 5.
Variatorul frontal cu rolă cilindrică, duo (fig. TRV-T.8.1.1.1,b): Mişcarea
şi momentul de torsiune de la arborele de intrare solidar cu discul
conducător 3 se transmiteprin frecare la rola
cilindrică 1, apoi tot prin frecare la discul condus 2. Forţa de
apăsare constantă, Q, este realizată de sistemul cu arc 4.
Sistemul de modificare a raportului de transmitere realizează
modificarea turaţiei la ieşire ca urmare a modificării razelor
de contact R1x şi R2x prin
intermediul mecanismului şurub-piuliţă, 5. Variatorul frontal cu rolă biconică, duo (fig. TRV-T.8.1.1.1,b): Mişcarea şi momentul de torsiune de la arborele de intrare se transmite la discul conducător 1, prin frecare la rola biconică 3 şi de la aceasta prin frecare la discul condus 2. Forţa de apăsare constantă Q, este realizată de sistemul cu arc de compresiune. Sistemul de modificare a raportului de transmitere realizează modificarea turaţiei la ieşire ca urmare a modificării razelor de contact R1x şi R2x prin intermediul mecanismului şurub-piuliţă, 4. În fer. TFR-S.1 se prezintă soluţia constructivă a unui variator frontal cu rola biconică cu sistem de apăsare dependent de sarcină bazat pe cuplaj cu bile. |
||
|
|
|
|
|
a |
b |
c |
|
Fig.
TFR-T.2.8.1.1.1
Variatoare frontale cu rolă: a – cilindrică, mono; b – cilindrică, duo |
||
|
|
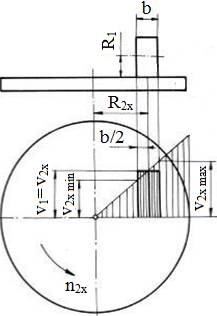
Parametri funcţionali principali: - rapoartele de transmitere (instantaneu, minim, maxim): ix = n1/n2x = R2x/R1, imin = n1/n2max = R2min/R1, respectiv, imax = n1/n2min = R2max/R1, pentru variatoarele mono; ix = n1/n2x = R2x/R1x, imin = n1/n2max = R2min/R1max, respectiv, imax = n1/n2min = R2max/R1min, pentru variatoarele duo; - gama de reglare a turaţiei,
pentru varianta mono (fig. TFR-T.2.8.1.1.1,a), în relaţiile de mai sus se consideră, R1min = R1max = R1.
-
alunecarea geometrică
(fig.
TFR-T.2.8.1.1.3),
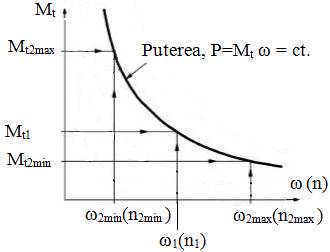
- caracteristica funcţională din fig. TFR-T.2.8.1.1.2 este definită de cazul funcţional, P2 = const. (fig. TFR-T.2.6.1,d), ce presupune folosirea integrală a puterii motorului de antrenare. Condiţia transmiterii momentului de torsiune, în cazul P2 = const.,
µ Fn max R1min = c Mt1 (TFR-T.2.8.1.1.3)
unde, µ este coeficientul de frecare de alunecare (corespunzător materialelor elementelor în contact), Fn max - forţa normală maximă din contactul de la raza R1min (R1min = R1, pentru varianta mono), c - coeficientul de siguranţă la alunecare (c = 1,15 ... 1,25). Forţa de apăsare (pentru variantele cu apăsare constantă),
asigură forţa de frecare necesară antrenării prin frecare a discului condus în orice poziţie a contactelor. Obs. Micşorarea alunecării geometrice se poate realiza prin executarea unor role cu lăţimi mici sau chiar cu profil semicircular, la care contactul teoretic este punctiform şi/sau a unor discuri conduse cu raza minimă cu valori cât mai mari posibil (deşi gabaritul creşte); utilizarea rolei biconice (fig. TFR-T.2.8.1.1.1,c) reduce substanţial alunecările geometrice ca urmare a lungimii reduse a liniei de contact |
|
Fig.
TFR-T.2.8.1.1.2
Caracteristica funcţională, Mt - ω |
|
|
|
|
|
Fig.
TFR-T.2.8.1.1.3
Schema de calcul a
alunecărilor geometrice |
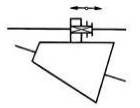
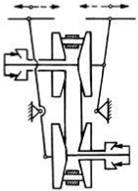
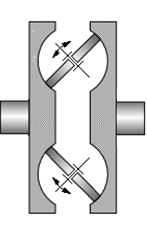
TFR-T.2.8.1.2 Variatoare sferice
|
Fig. TFR-T.2.8.1.2.1 Schema de calcul a variatorului sferic |
Funcţionare: Momentul de torsiune Mt1 se transmite de la arborele de intrare prin sistemul de apăsare 4, prin discul conic 1, prin frecare la corpurile sferice 3 (dispuse echiunghiular) şi de la acestea, de asemenea prin frecare, la discul conic condus 2. Modificarea raportului de transmitere (a celor două raze de contact) se realizează prin rotirea sincronă a braţelor suport 5. Corpurile sferice 3 sunt ţinute în contact de inelul rotitor 5. Forţa de apăsare, necesară transmiterii sarcinii prin frecare, se realizează prin sistemul de apăsare 4 care împinge axial discul 1 cu o forţă dependentă de momentul de torsiune transmis. În fer. TFR-S.2 se prezintă o soluţie constructivă a unui variatoar sferic. Parametri funcţionali principali: - rapoartele de transmitere (instantaneu, minim, maxim):
imin = n1/n2min = R1min/R2max şi, respectiv, imax = n1/n2max = R1max/R2min. unde, R1x, R2x sunt razele contactelor elementului sferic 3 cu discul 1, şi respectiv cu discul 2; R3 - raza sferei 3, γ - unghiul de înclinare a axei sferei (γ = 0, axa sferei este paralelă cu axele discurilor şi ix = 1), α - semiunghiul conurilor (α = 40o... 50o); în această relaţie se adoptă semnele poziţionate sus, când axele rolelor sunt înclinate spre stânga (variatorul este reductor), şi poziţionate jos, când acestea sunt înclinate spre dreapta (fig. TFR-T.2.8.1.2.1.1 variatorul este amplificator). - gama de reglare a turaţiei,
unde Rmax, Rmin sunt razele de contact (R1x, R2x) maximă şi minimă. |
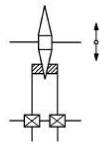
TFR-T.2.8.1.3 Variatoare toroidale
|
|
|
În funcţie de formele suprafeţelor toroidale se pot defini două variante: variatoare toroidale semicomplete (fig. TFR-T.2.8.1.3.1,a), variatoare toroidale complete (fig. TFR-T.2.8.1.3.1,b) care realizează game de reglare mai mari. Funcţionare: Momentul de torsiune Mt1 se transmite de la arborele de intrare prin sistemul de apăsare 4, prin discul toroidal 1, prin frecare la rolele 3 şi de la acestea, de asemenea prin frecare, la discul toroidal condus 2. Modificarea raportului de transmitere (a celor două raze de contact) se realizează prin rotirea sincronă a braţelor suport 5. Forţa de apăsare, necesară transmiterii sarcinii prin frecare, se realizează prin sistemul de apăsare 4 care împinge axial discul 1 cu o forţă dependentă de momentul de torsiune transmis. În fer. TFR-S.3 se prezintă soluţiile constructive ale unor variatoare care au la bază cele două variante. Parametri funcţionali principali: - rapoartele de transmitere (instantaneu, minim, maxim):
imin = n1/n2max = Rmin/Rmax şi, respectiv, imax = n1/n2min = Rmax/Rmin. unde, R1x, R2x sunt razele contactelor dintre rola 3 cu discul 1, şi respectiv cu discul 2; R - raza de curbură a zonelor active ale discurilor 1 şi 2, γ - semiunghiul rolei (constant), αmin ≤ α ≤ αmax - unghiurile poziţiilor axelor rolelor; în această relaţie se adoptă semnele de sus când axele rolelor sunt înclinate spre stânga (variatorul este amplificator) şi cele de jos când acestea sunt înclinate spre dreapta (fig. TFR-T.2.8.1.3.1,c, variatorul este reductor). - gama de reglare a turaţiei,
unde Rmax, Rmin sunt razele de contact maximă şi minimă. |
|
a |
b |
|
|
|
||
|
c |
||
|
TFR-T.2.8.1.3.1 Variatorul toroidal: a – varianta toroid semicomplet; b - varianta toroid complet; c - schema funcţională a variatorului semitoroidal |
||
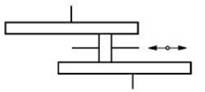
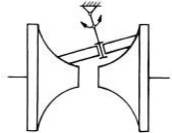
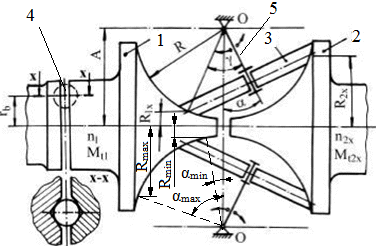
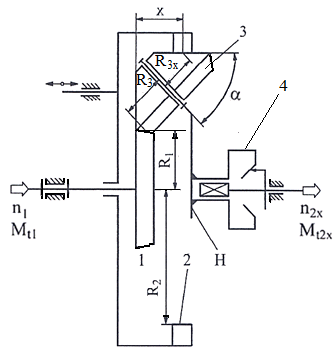
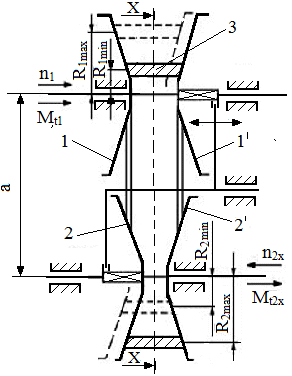
TFR-T.2.8.1.4 Variatoare planetare cu role conice
|
TFR-T.2.8.1.4.1 Schema funcţională a variatorului planetar |
Funcţionare: Momentul de torsiune Mt1 se transmite de la discul conic 1 prin frecare la rolele 3 (dispuse echiunghiular) şi de la acestea prin braţele portsatelit H şi sistemul de apăsare 4 la arborele de ieşire. Modificarea raportului de transmitere se realizează prin deplasarea axială a inelului 2. Forţa de apăsare, necesară transmiterii sarcinii prin frecare, se realizează prin sistemul de apăsare 4 care împinge axial braţele H şi rolele 3 cu o forţă dependentă de momentul de torsiune transmis. În fer. TFR-S.4 se prezintă o soluţie constructivă a unui variatoar planetar. Parametri funcţionali principali: - rapoartele de transmitere (instantaneu, minim, maxim):
imin = n1/n2max = 1 - (R3/R1)/(R2/R3min) şi, respectiv, imax = n1/n2min = 1 - (R3/R1)/(R2/R3max),
unde,
R3x
este raza rolei 3 în contact cu inelul 2,
R2
- raza inelului 2,
R3 - raza
rolei 3 în contact cu discul 1 (constantă), R1 - raza
discului 1 în contact cu rola 3 (constantă),
α - unghiul de
înclinare a rolei conice 3, x - poziţia inelului 2 în raport cu rola 3; - gama de reglare a turaţiei,
|
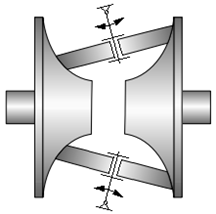
TFR-T.2.8.1.5 Variatoare cu conuri deplasabile şi element (inel) rigid
|
a
b Fig. TFR-T.2.8.1.5.1 Variator cu conuri deplasabile şi element (inel) rigid: a – schema axială; b - schema procesului de autoîmpănare |
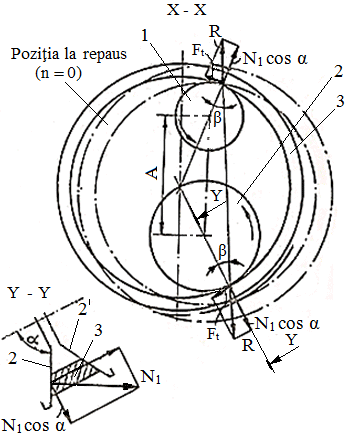
Funcţionare: Momentul de torsiune Mt1 se transmite de la discurile conice 1, 1' prin frecare la inelul rigid 3 şi de la acestea, de asemenea prin frecare, prin discurile conice 2, 2' la arborele de ieşire. Modificarea raportului de transmitere se realizează prin deplasarea axială, simultan a discurilor 2, 2'. Forţa de apăsare, necesară transmiterii sarcinii prin frecare, se realizează automat în urma îndeplinirii condiţiilor de autoîmpănare a inelului în interstiţiile dintre conurile conducătoare respectiv cele conduse. Autoîmpănarea elementului (inelului) rigid 3 se realizează consecinţă a efectului de pană rezultat ca urmare a existenţei unghiului de împănare β (cu valori mici), dintre forţele radiale (N1cos α) şi forţele rezultante, R (fig. TFR-T.2.8.1.5.1,b); ca atare, unghiul de presiune (complementul unghiului de împănare β) are valori mari şi se realizează condiţii optime de transmitere a forţei în zonele de contact dintre inelul liber 3 şi discurile conice 1, 1', 2, 2'. Greutatea proprie a elementului (inelului) rigid 3 constituie forţa de apăsare iniţială necesară iniţierii transmiterii sarcinii la pornire. În fer. TFR-S.5 se prezintă o soluţie constructivă a unui variator cu conuri deplasabile şi element (inel) rigid. Parametri funcţionali principali: - rapoartele de transmitere (instantaneu, minim, maxim):
ix = n1/n2x = R2x/R1x, imin = n1/n2max = R2min/R1max, respectiv, imax = n1/n2min = R2max/R1min;
- gama de reglare a turaţiei,
unde R1max, R1min, R2max, R2min sunt razele de contact maxime şi minime. Condiţia de transmitere a sarcinii prin frecare:
c Ft = 2 µ N1, (TFR-T.2.8.1.5.2)
unde, c este coeficientul de siguranţă la patinare (alunecare); Ft = Mt1/ R1min - forţa tangenţială utilă maximă (transmisă prin frecare); µ - coeficientul de frecare de alunecare al materialelor inelului rigid şi discurilor conice; N1 - forţa normală din contactele active. Condiţia de împănare (apăsare automată):
Ft = 2 N1 cosα tgβ (TFR-T.2.8.1.5.3)
unde, Ft = Mt1/ R1max - forţa tangenţială utilă minimă (transmisă prin frecare), N1 - forţa normală din contacte, α - semiunghiul conurilor, β - unghiul de împănare. Obs. Din relaţiile (TFR-T.2.8.1.5.2) şi (TFR-T.2.8.1.5.3) rezultă condiţia,
care evidenţiază independenţa coeficientului de siguranţă la patinare faţă de raportul de transmitere; din această relaţie se poate determina unghiul maxim de împănare β care asigură împănarea şi transmiterea sarcinii. |
TFR-T.2.8.1.6 Variatoare cu conuri deplasabile şi element flexibil de tip curea (nemetalică) sau articulat (lanţ)
|
a
b
c Fig. TFR-T.2.8.1.6.1 Scheme funcţionale: a – de multiplicare; b – de reducere; c – de forţe |
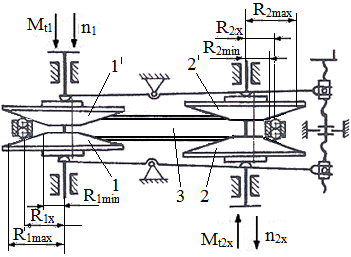
Funcţionare: Variatoarele cu conuri deplasabile se compun din două perechi de conuri montate pe arborii de intrare I (fig. TFR-T.2.8.1.6.1) şi de ieşire II. Poziţia celor două conuri, pentru modificarea raportului de transmitere, poate fi reglată prin menţinerea unui con fix şi deplasarea axială a celuilalt sau prin deplasarea axială, simultană, a ambelor conuri.
Parametri funcţionali principali: - rapoartele de transmitere (instantaneu, minim, maxim):
ix = n1/n2x = R2x/R1x, imin = n1/n2max = R2min/R1max şi, respectiv, imax = n1/n2min = R2max/R1min,
unde, R1x, R2x sunt razele contactelor. - gama de reglare a turaţiei,
unde, R1max, R1min, R2max, R2minsunt razele de contact maxime şi minime.
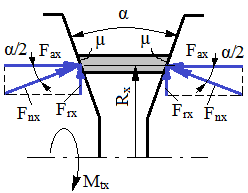
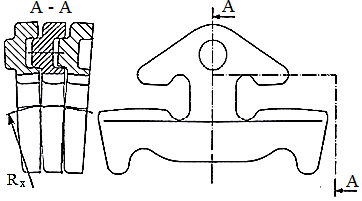
Condiţia de transmitere a sarcinii prin frecare într-o poziţie oarecare a elementului flexibil:
2µ Fnx Rx = c Mtx, (TFR-T.2.8.1.6.1.2)
unde, c este coeficientul de siguranţă la patinare (alunecare); Fnx - forţa normală de apăsare; µ - coeficientul de frecare de alunecare al materialelor elementului flexibil şi discurilor conice; Mtx - momentul de torsiune transmis; Rx - raza de contact. Din relaţia (TFR-T.2.8.1.6.1.2), ţinând cont de fig. TFR-T.2.8.1.6.1, rezultă forţa axială de apăsare a discurilor,
şi forţa radială de încărcare a arborelui,
|
TFR-T.2.8.1.6.1 Variatoare cu conuri deplasabile şi element flexibil de tip curea (nemetalică) sau articulat (lanţ) prin tragere
|
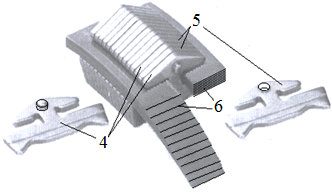
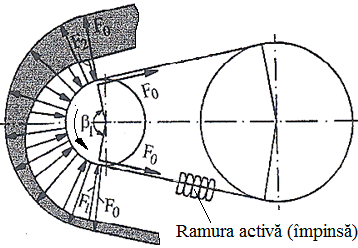
Funcţionare: Momentul de torsiune Mt1 se transmite de la discurile conice 1, 1' prin frecare la elementul flexibil (lanţ) 3 şi de la acestea, de asemenea prin frecare, prin discurile conice 2, 2' la arborele de ieşire. Modificarea raportului de transmitere se realizează prin deplasarea axială, simultan a discurilor 1, 1' şi 2, 2'. În fer. TFR-S.6 se prezintă o soluţie constructivă a unui variatoar cu element flexibil de tip curea sau articulat de tip lanţ prin tragere. Aceste variatoare sunt caracterizate de forţe mărite (mai mari decât forţa de pretensionare, fig. TFR-T.2.8.1.6.1.1) în ramura activă şi forţe reduse în ramura pasivă (mai mici decât forţa de pretensionare). Elementele articulate metalice de tip lanţ, frecvent utilizate în practică, pot avea diverse configuraţii. În fig. TFR-T.2.8.1.6.1.2 se prezintă trei soluţii constructive care se diferenţiază prin nivelul de implementare a soluţiilor ce implică frecări de rostogolire (randamente ridicate). |
|
|
|
|
|
a |
b |
|
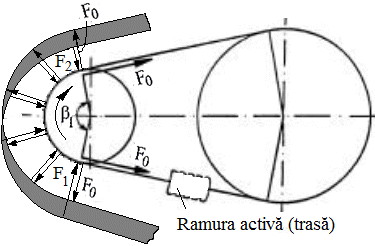
Fig. TFR-T.2.8.1.6.1.1 Variator cu conuri deplasabile şi element flexibil articulat metalic prin tragere: a – schema funcţională; b - schema forţelor |
|
|
|
|
|
|
a |
b |
c |
|
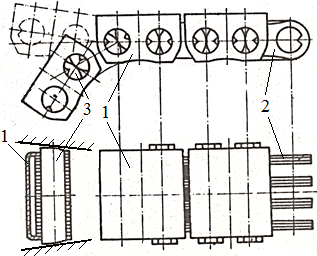
Fig. TFR-T.2.8.1.6.1.2 Elemente metalice articulate (lanţuri) : a – lanţuri cu bolţuri şi eclise decupate (1 - eclisă exterioară, 2 - eclisă interioară, bolţ); b – lanţuri cu inele (1 - inel, 2 - eclisă, 3 - inel elastic, 4 - bolţ); c – lanţuri cu role (1 - eclisă exterioară, 2 - rolă, 3 - eclisă interioară, 4 - bolţ) |
||
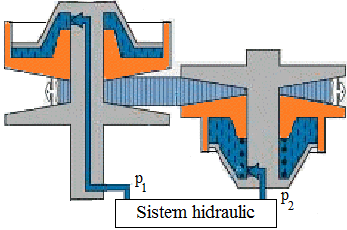
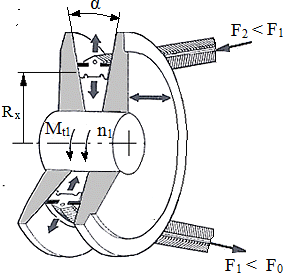
TFR-T.2.8.1.6.2 Variatoare cu conuri deplasabile şi element flexibil metalic prin împingere (Van Doorne)
|
a b
c d
e f
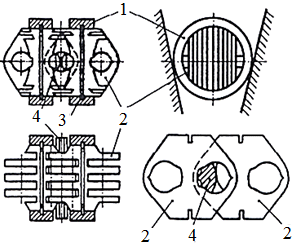
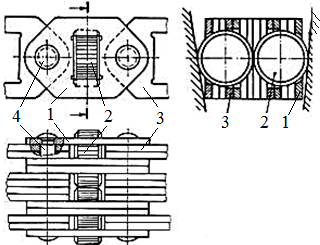
Fig. TFR-T.2.8.1.6.2.1 Variator cu conuri deplasabile şi element flexibil metalic prin împingere: a – schema funcţională; b - schema sistemului de modificare a raportului de transmitere şi de apăsare; c - structura constructivă a elementului flexibil de împingere (3 - segment cu proeminenţă, 2 - segment cu altezaj, 3 - benzi metalice circulare); d - asamblarea segmenţilor; e, f - schemele forţelor |
Funcţionare: Momentul de torsiune Mt1 se transmite de la discurile conice 1, 1' prin frecare la elementul flexibil de împingere 3 şi de la acestea, de asemenea prin frecare, prin discurile conice 2, 2' la arborele de ieşire. Modificarea raportului de transmitere se realizează prin deplasarea axială cu motoare hidraulice, simultan a discurilor 1 şi 2'. Transmiterea forţei prin elementul flexibil 3 se realizează prin contactul direct (formă) dintre segmenţii 4 şi 5 (fig. TFR-T.2.8.1.6.2.1,c,d) susţinuţi cele două seturi de benzi metalice 6. Parametri funcţionali principali: - rapoartele de transmitere (instantaneu, minim, maxim): ix = n1/n2max = R2x/R1x, imin = n1/n2max = R2min/R1max, respectiv, imax = n1/n2min = R2max/R1min. unde, R1x, R2x sunt razele contactelor - gama de reglare a turaţiei,
(TFR-T.2.8.1.6.2.1) unde, R1max, R1min, R2max, R2min sunt razele de contact maxime şi minime. - forţele statice: Momentul la arborele conducător transmis prin ramura activă (comprimată) se determină cu relaţia, Mt1 = (F1 - F2) R1min (TFR-T.2.8.1.6.2.2) în care, F1 este forţa din ramura activă (comprimată), F2 - forţa din ramura pasivă; pentru o bună funcţionare ramura activă (împinsă) trebuie să rămână întinsă F1 < F0 şi se consideră F1 = Ks F0, cu Ks =1,2 ...1,4 - factor de siguranţă şi F0, - forţa de întindere iniţială a elementului flexibil. Din relaţia lui Euler (v. cap. Transmisii prin curele), aplicată pentru acest caz,
ţinând cont de relaţia (TFR-T.2.8.1.6.2.2) se oţine valoarea forţei maxime de împingere,
şi a forţei de întindere iniţială,
unde µ = µr/cos(α/2) - coeficientul de frecare redus, µr - coeficientul de frecare asociat cuplului de materiale în contact, α - unghiul segmenţilor elementului flexibil, β1 - unghiul de înfăşurare a elementului flexibil pe discurile conducătoare. |
|
Obs. Asigurarea unei apăsări foarte mari pentru menţinerea unui contact ferm între elementele de frecare vor conduce la pierderi mai mari de putere în cureaua metalică şi în lagăre. Astfel, în toate punctele de funcţionare a variatorelelor va exista un conflict între necesitatea asigurării unei presiuni de contact suficiente pentru transmiterea sarcinii prin frecare , pe de-o parte, şi necesitatea minimizării pierderilor de putere ce afectează randamentul şi a eforturilor de contact ce afectează durabilitatea, pe de altă parte. În fer. TFR-S.7 se prezintă o soluţie constructivă de utilizare a variatorului de tip Van Dorne în transmisiile automobilelor. |
|
TFR-T.2.8.2 Model de
calcul la solicitarea de contact
|
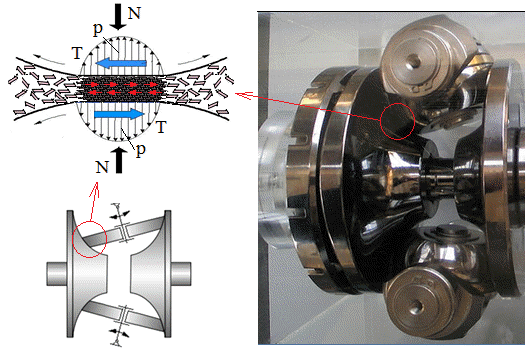
a
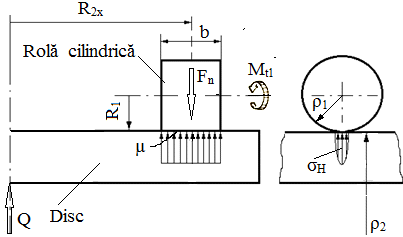
b Fig. TFR-T.2.8.2.1 Schema de calcul la contact: a – modelul lui Hertz; b – modelul de calcul la contact al variatorului frontal cu rolă cilindrică |
Pentru variatoarele prin fricţiune care
funcţionează cu ungere, forma principală de deteriorare este
oboseala de contact (pitingul) şi pentru evitarea acesteia este necesar
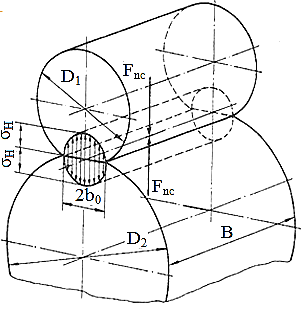
calculul la solicitarea de contact. Modelul de calcul la solicitarea de contact liniar de referinţă [Hertz, 1881] ( fig. TRV-T.8.1,a) În zona de contact a doi cilindri cu diametrele D1,2
şi lungimi B, încărcaţi cu forţa Fnc,
apar tensiuni maxime normale de contact care, conform lui Hertz, se
determină cu relaţia,
factorul de elasticitate, unde E1,2 şi ν1,2
sunt modulele de elasticitate şi, respectiv, coeficenţii
contracţiei transversale (Poisson) ai materialelor celor doi
cilindri şi
tensiunea admisibilă la
contact, unde
σHlim – tensiunea limită la contact, SHmin – coeficientul minim de
siguranţă la oboseala de contact a materialului. Ipotezele
modelului lui Hertz: materialele
corpurilor sunt omogene, izotrope, elastice după legea lui Hooke;
forţa normală este aplicată static; tensiunile de contact se
repartizează uniform pe lungimea de contact; suprafeţele
cilindrilor sunt perfect netede; nu se iau în considerare forţele de
frecare. Calculul la solicitarea de contact a transmisiilor prin fricţiune cu raport de transmitere variabil
Personalizarea
parametrilor modelului lui Hertz pentru contactul variatorului frontal ( fig. TFR-T.2.8.2.1,b; TFR-T.2.8.1.1,a ): ρ1 = R1, ρ2 = ∞, lk = b,
pentru cazul, momentul rezistent Mt2 = const. (v. fig. TFR-T.2.6.1, c) sau
pentru cazul, puterea rezistentă P2 = const. (v. fig. TFR-T.2.6.1, d; rel. (TFR-T.2.7.5) ). În aceste relaţii, µ este coeficientul de frecare de alunecare dintre suprafeţele în contact, c – coeficientul de siguranţă la alunecare, ηmin - randamentul minim. |


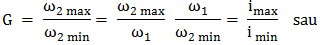
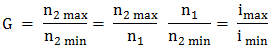
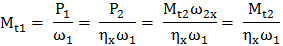
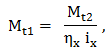
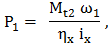
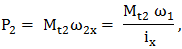
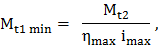
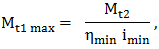
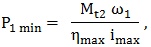
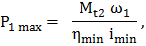
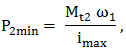
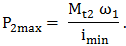
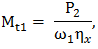
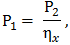
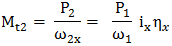
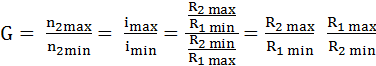
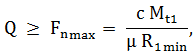
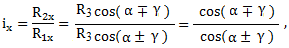
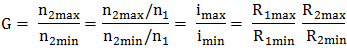
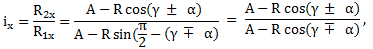
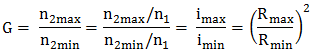
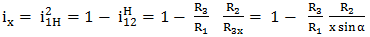 ,
, 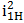 -
raportul de transmitere a mişcării de la discul 1 la braţul portsatelit 4 cu
inelul 2 fix (transmisie prin fricţiune cu axă mobilă);
-
raportul de transmitere a mişcării de la discul 1 la braţul portsatelit 4 cu
inelul 2 fix (transmisie prin fricţiune cu axă mobilă);
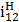 -
- 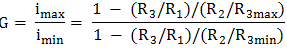
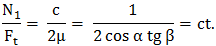
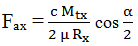
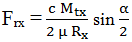
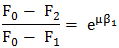
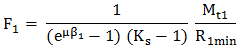 ,
,
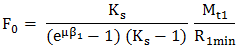 ,
,