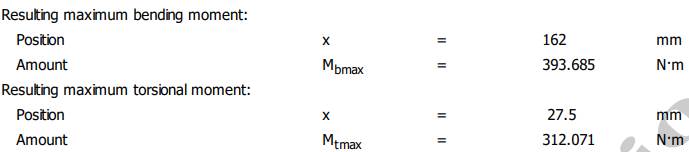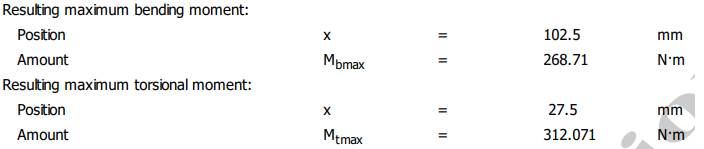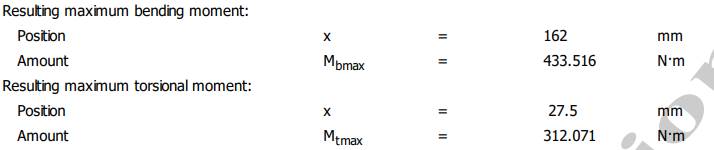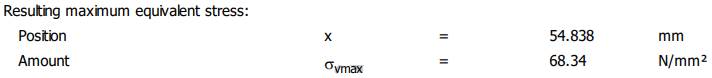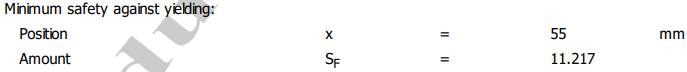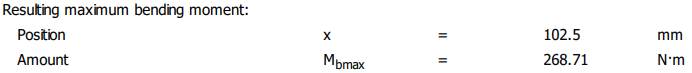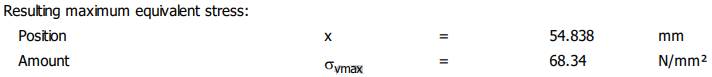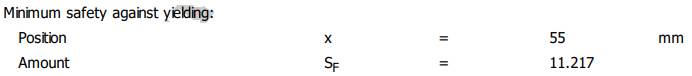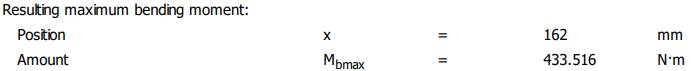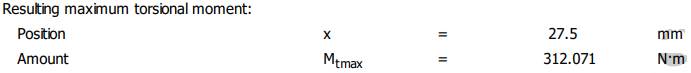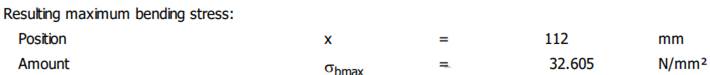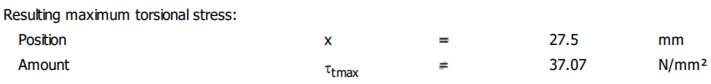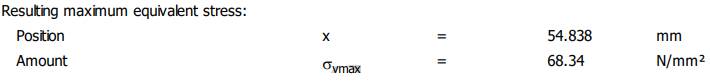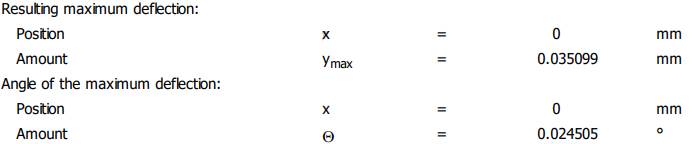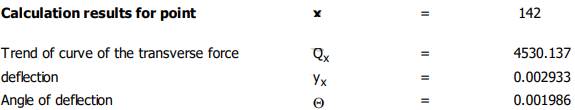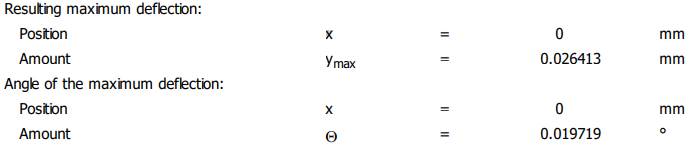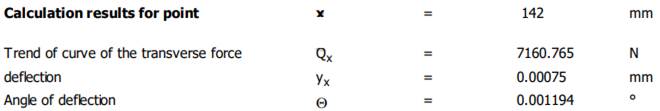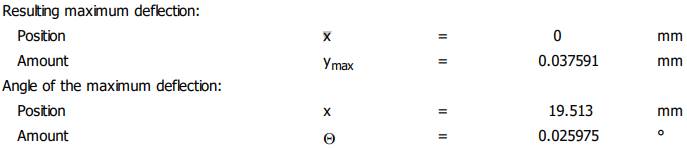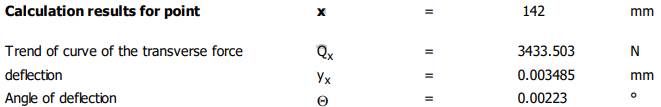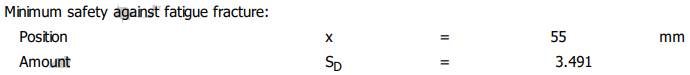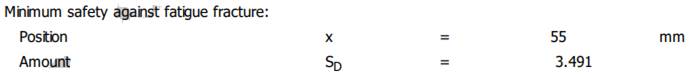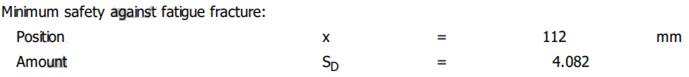Mogan Gh.L., Butilă E.V., Buzdugan I.D. Proiectarea reductoarelor cilindrice. Universitatea Transilvania din Brașov

Ghid 13.1 Verificare arbore de intrare cu MDESIGN

1. SCHEME DE ÎNCĂRCARE A ARBORELUI DE INTRARE

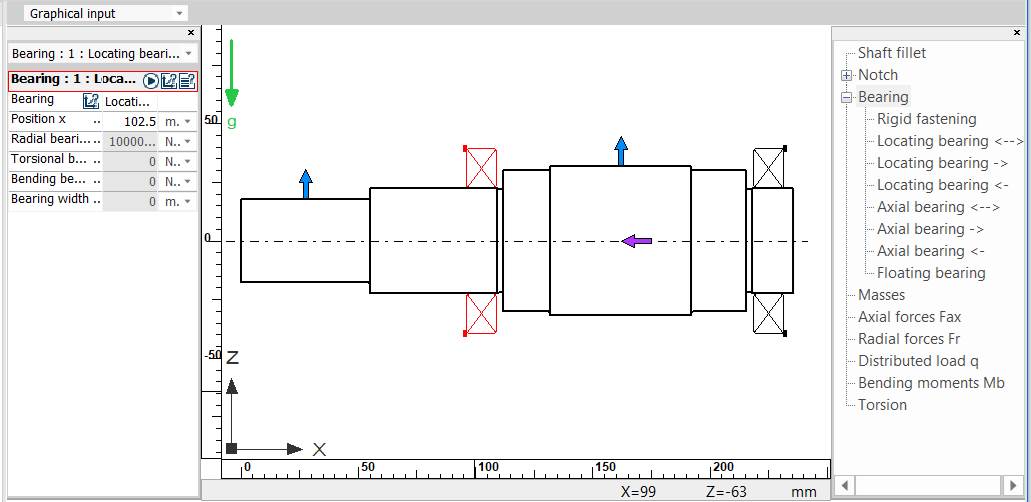
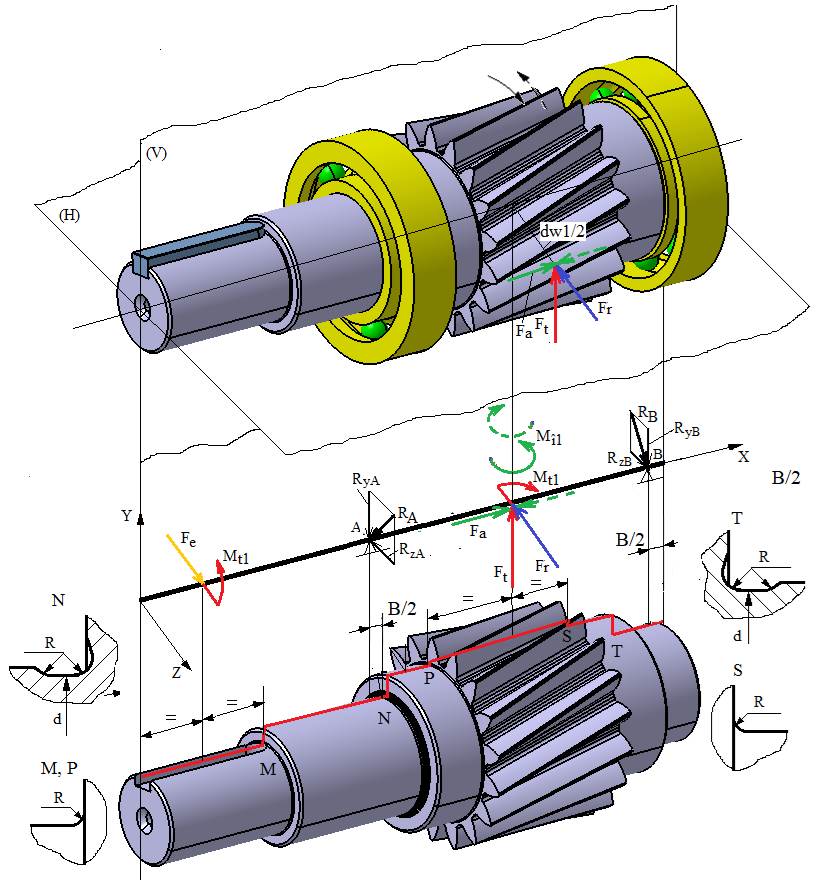
1.1 Schema de încărcare a arborelui de intrare al RCil H

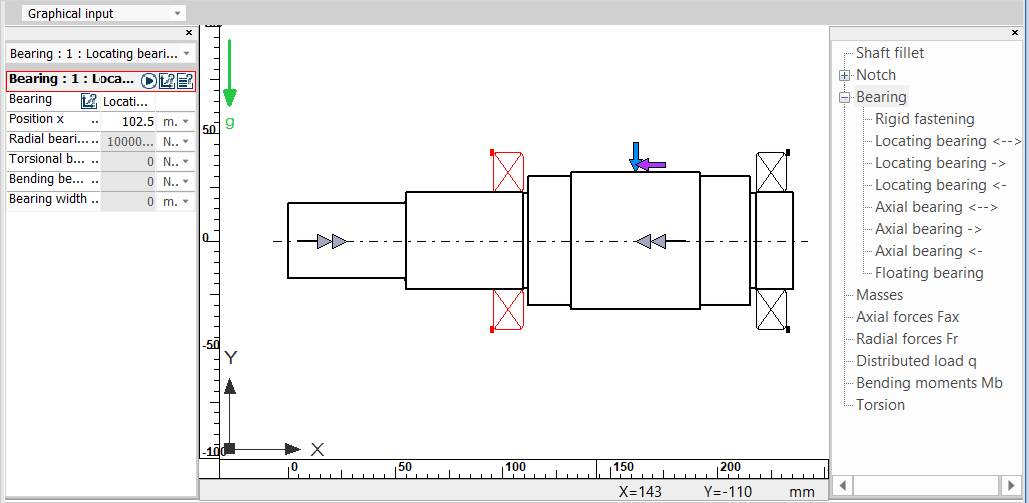
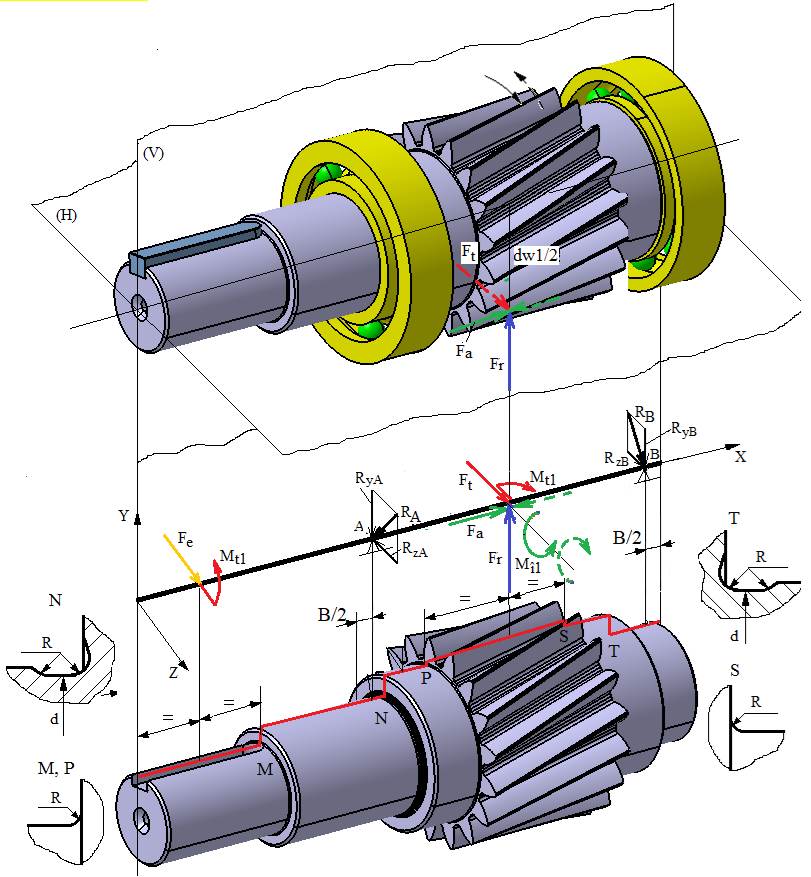
1.2 Schema de încărcare a arborelui de intrare al RCil Vs

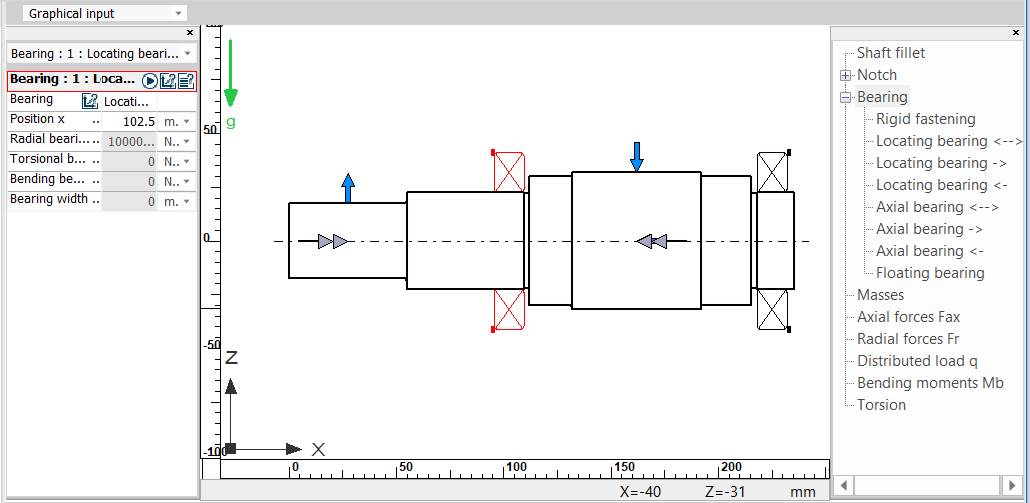
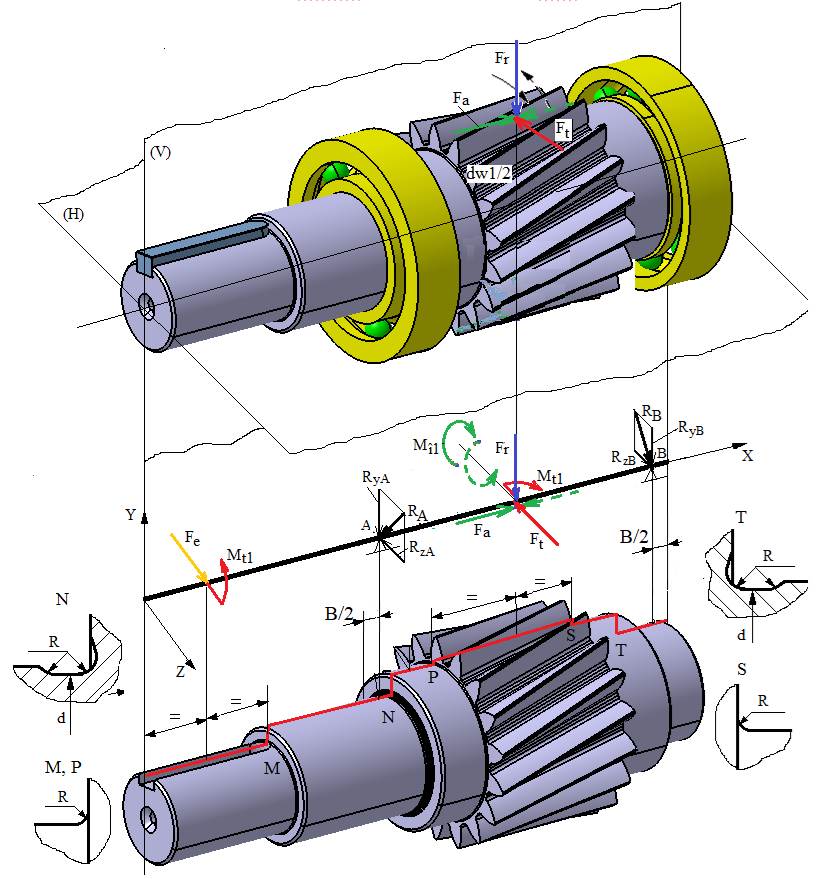
1.3 Schema de încărcare a arborelui de intrare al RCil Vj

2. DATE DE INTRARE

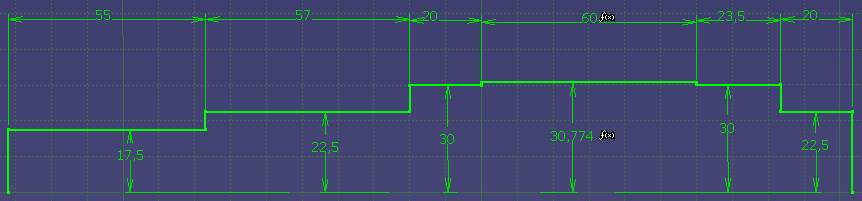
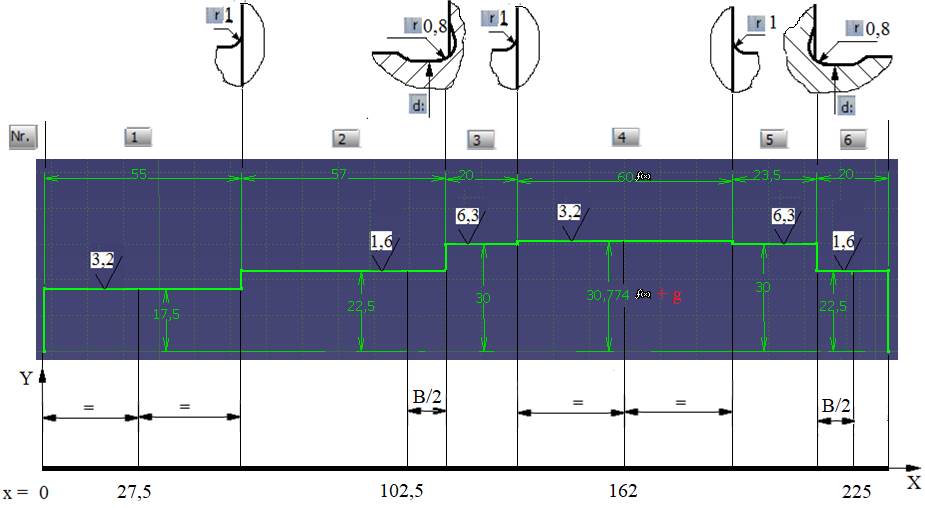
Schema geometriei arborelui, conform schiță CATIA

Valori diametre şi lungimi

Diametrele și lungimile tronsoanelor: conform schiței CATIA (v. schema de mai sus).

Distanțe de poziţionare a reacţiunilor (v. schemele 1.1, 1.2 și 1.3), B = 19 mm, din catalogul de rulmenţi (Ex.4.3);

Grosimea coroanei dinţate, g = 1 mm (v. Ghid.9.1).

Diametrul de rostogolire al pinionului, d_w1 = 71,1628 mm (v. Ex.6.1).

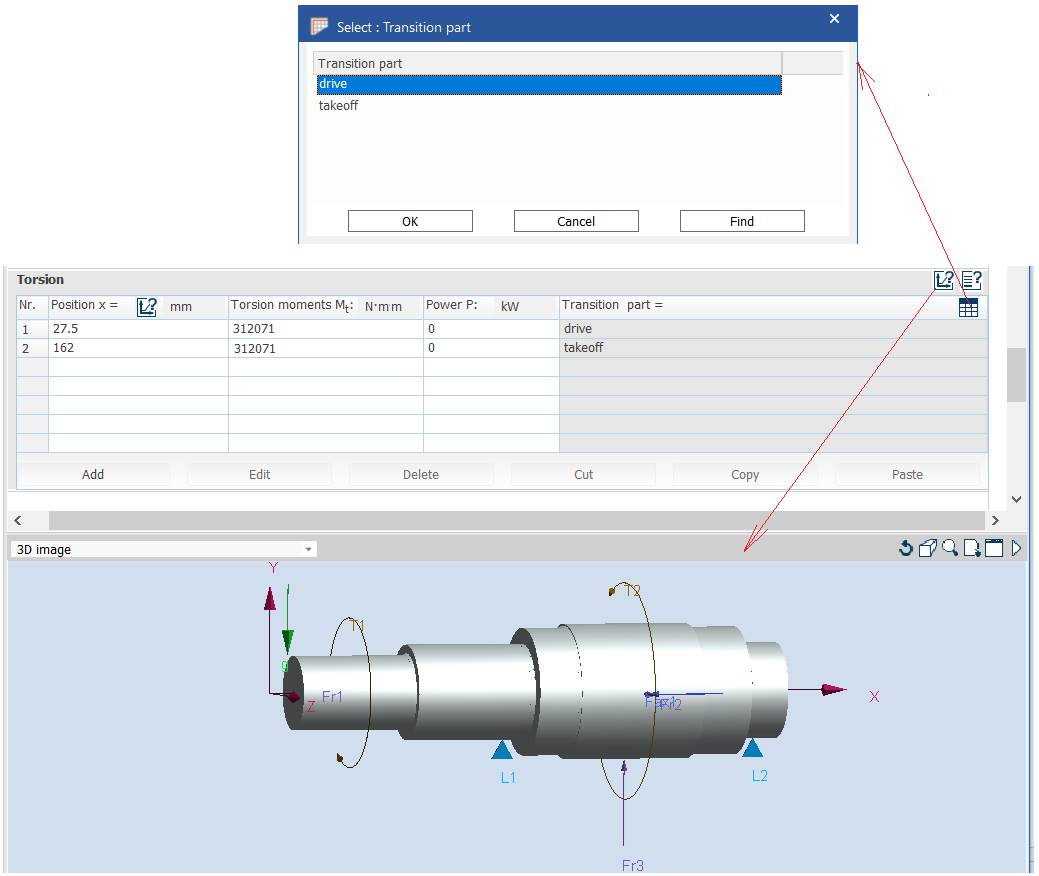
Valori forţe şi momente

Momentul de torsiune, M_t1 = 312071 Nmm (Ex.2.2).

Forţele de încărcare a pinionului cilindric: tangenţială, = 8770,6 N; radială, = 3582,8 N; axială, F_a = 2350 N (Ex.7).

Forţa de încărcare a capului arborelui, se adoptă ca ex. F_e = = 3582,8 N.

Obs. Această valoare poate fi modificată în funcție de încărcarea exterioară a capului arborelui de intrare (de ex. încărcare prin intermediul unei transmisii prin curele, dințate etc.).

Momentele de încovoiere, M_î1 = d_w1/2 = 83616,29 mm (Calc.0).

Turația arborelui

n = 625 rot/min, turaţia arborelui de intrare (Ex.2.2).

Valori parametri geometrici și tehnologici, conform MDESIGN

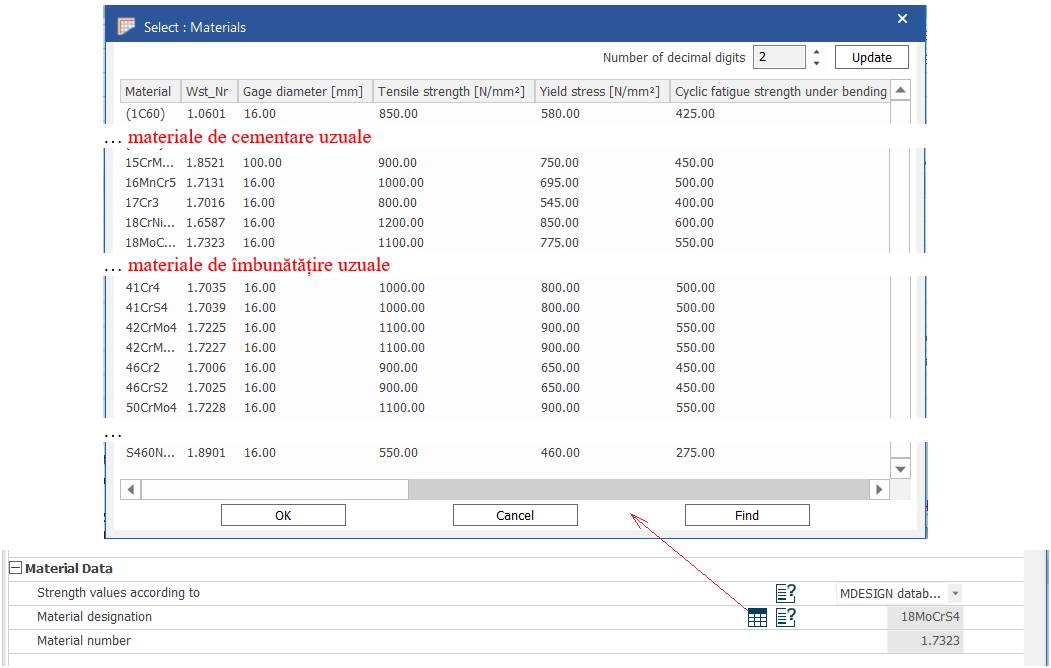
Date despre material

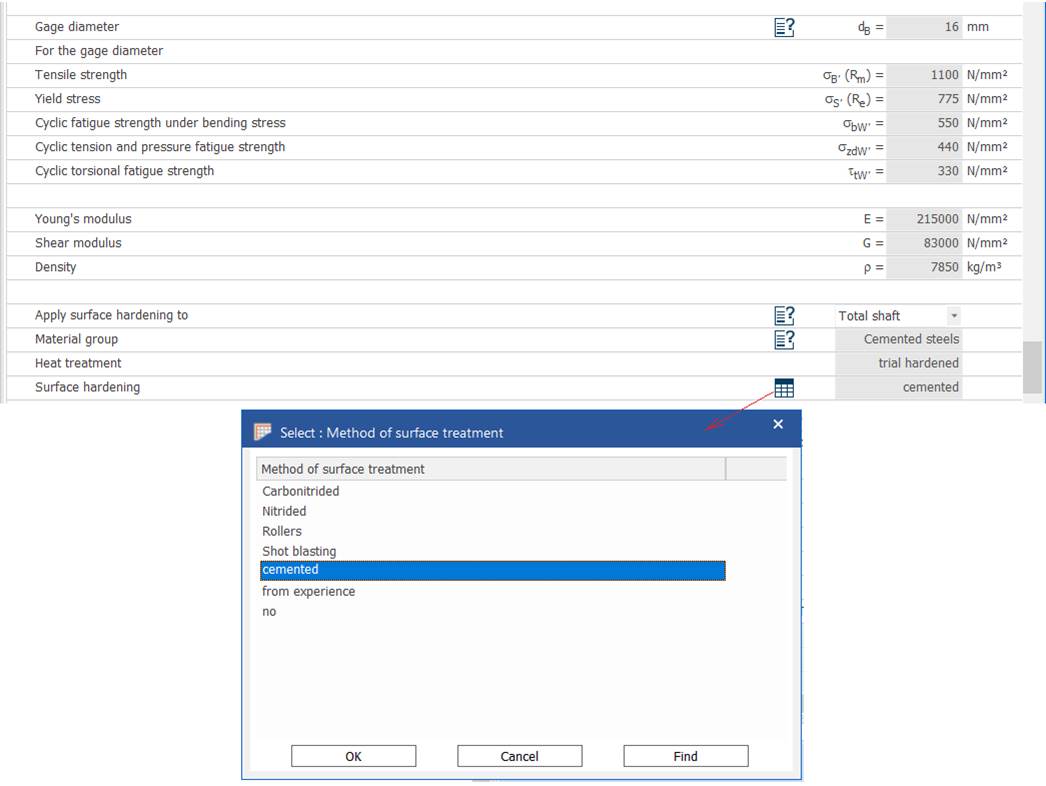
Tipul oţelului şi tratamentul termic: 18MoMnNi13, Cementare (carburare+călire+revenire înaltă) (Ex.4.2.1).

3. INTRODUCERE DATE ÎN MDESIGN

(Anexa.13.1.1 Descrierea modulului MDEIGN de calcul a arborilor drepţi)

3.1 Lansarea aplicaţiei MDESIGN

Deschiderea modulului MDESIGN shaft (extins)

¿

®

¿

sau Shaft, Standard

¿

®

¿

®

¿

®

¿

Salvarea aplicației

¿ (, ) ® : [ se va selecta folderul în care se va salva aplicația], [ se va introduce numele fișierului Arbore intrare H], [: ], ¿ [în titlul feresteri principale apare: ].

Deschiderea aplicației (generată și salvată anterior)

[se va selecta folderul în care a fost salvată aplicația] ® ¿

3.2 Selectarea ferestrei Input și setări generale

(Anexa.13.1.1 Descrierea modulului MDEIGN de calcul arbori)

Selectare pagina Input

Setări generale

Obs.

- opțiunea se va selecta pentru vizualizarea datelor obținute după etapa de rezolvare (calcul, v. cap. 4);

opțiunea se va selecta pentru vizualizarea datelor de intrare (v. subcap. următor).

3.2 Introducere parametri geometrici şi tehnologici

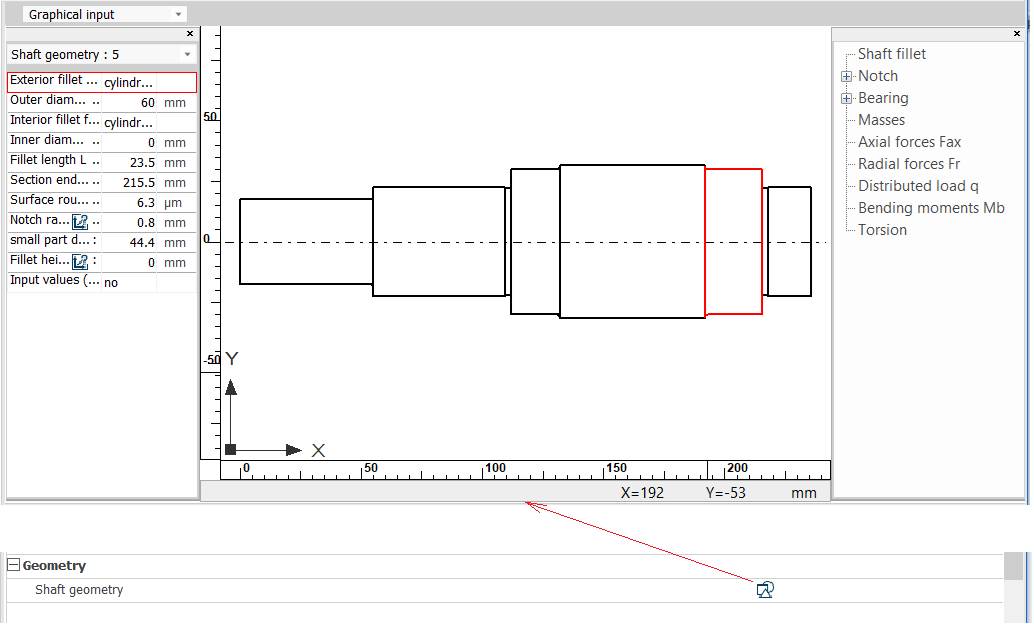
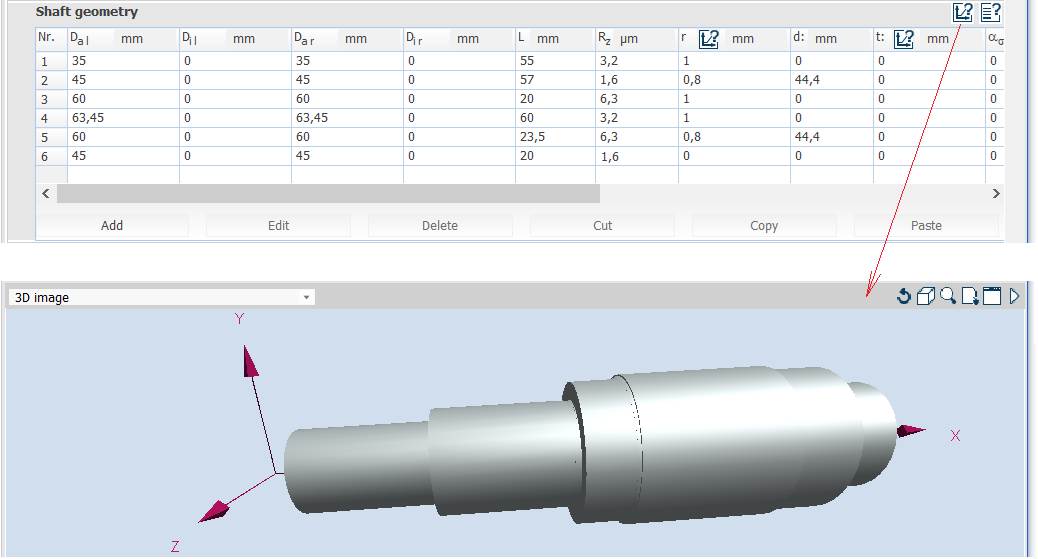
Introducere date în tabelul Shaft geometry

: ¿, [se introduc valori pentru tronsonul nr. 1: D_al (diametrul din stânga), D_ar (diametrul din dreapta), L (lungimea tronsonului), R_z (rugozitatea), r (raza racordării), d (diametrul arborelui în zona racordării) ].

[se repetă această succesiune și pentru celelalte tronsoane].

Obs. Vizualizarea modelului obținut se poate face în fereastrele și . Manipularea modelului se poate folosind:

¿ (, proiecție în plan, 2D;, vedere în perspectivă, 3D); ¿ + ¿ (pentru mărire) sau (pentru micșorare); ¿+ drag, pentru translatare; + drag, pentru rotire. După vizualizare se va revenei la pagina Input, v. subcap. 3.2).

Introducere date privind poziția punctului de calcul a săgeții la încovoiere; turația; considerarea greutății proprii, efectui giroscopic și rigidității rulmentului

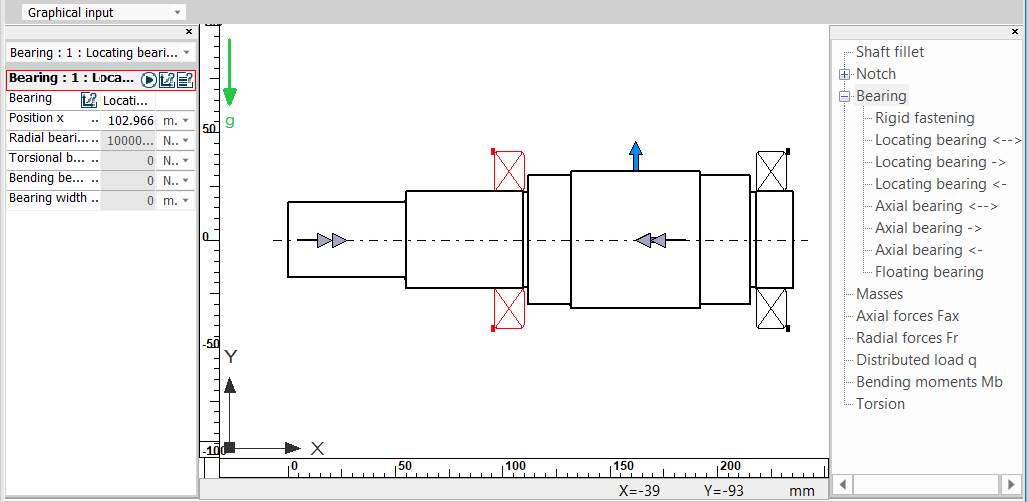
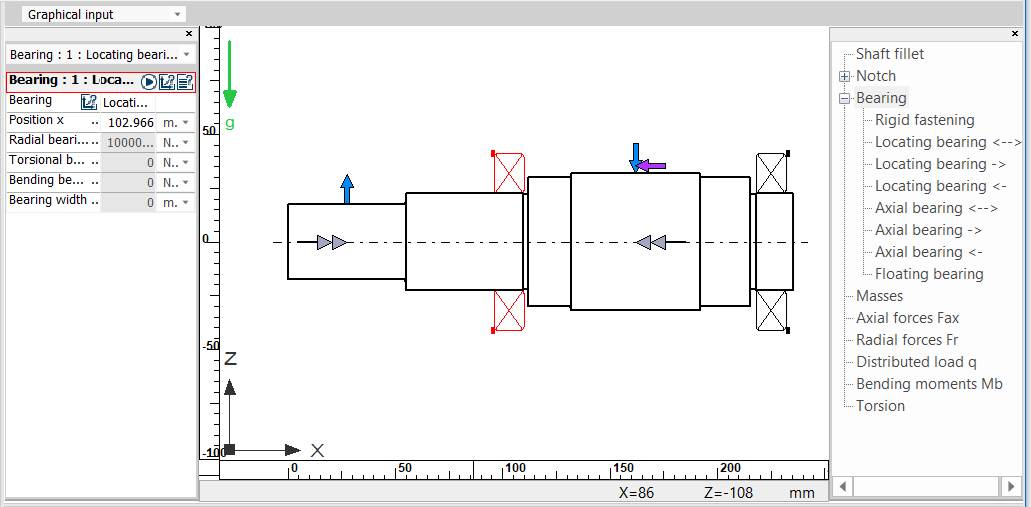
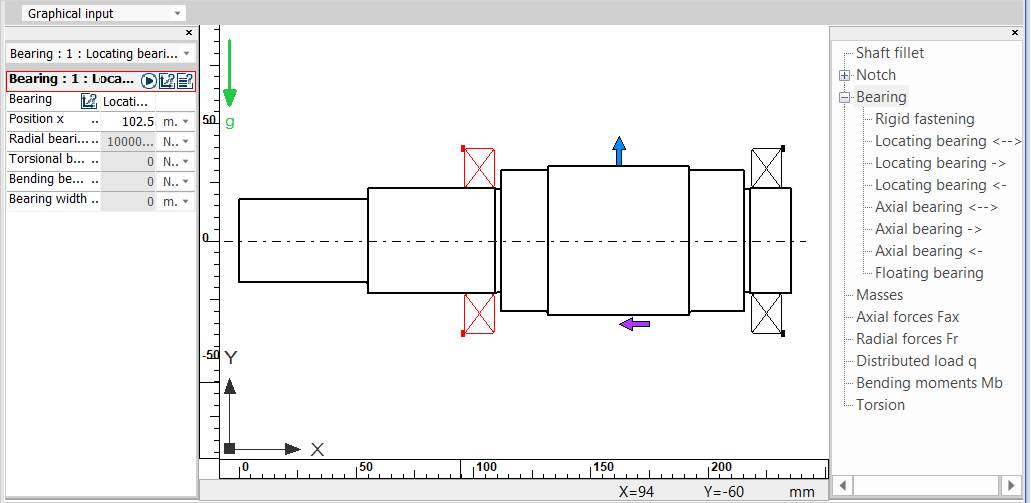
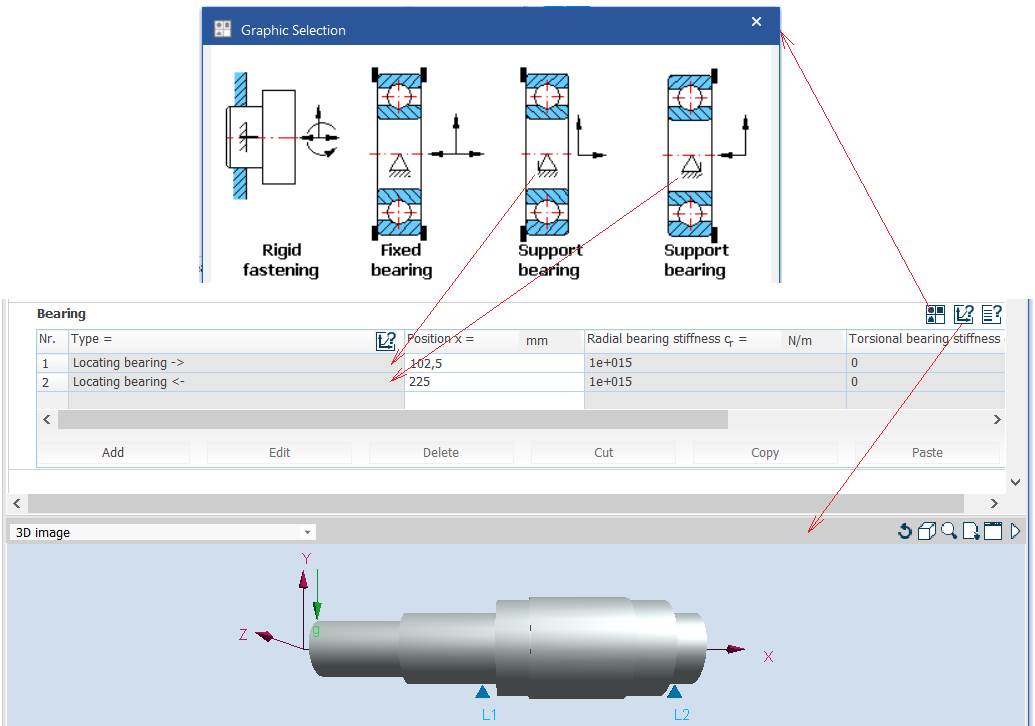
Obs.

- punctul de calcul a săgeților la încovoiere va fi mijlocul tronsonului cu dantură cilindrică;

- turația este egală cu turația arborelui;

- toți arborii RCil sunt orizontali;

- având în vedere că arborii ai RCil sunt scurți cu mase reduse se neglijează efectele giroscopice;

- deoarece rulmenții aleși au rigidități mărite, nu se iau în considerare efectul acestora.

Introducere date despre reazeme in tabelul Bearing

: ¿, ¿ ® : [se selecta cu ¿ pictograma cu rezemare în partea din stânga] : [se introduce valorea x (poziție), de ex. 102,5].

: ¿, ¿ ® : [se selecta cu ¿ pictograma cu rezemare în partea din dreapta] : [se introduce valorea x (poziție), de ex. 225].

Obs.

- tipurile rezemărilor se iau în considerare și corelat cu schema de montaj adoptată (v. Ex.4.3);

- valoarea rigidității radiale se va genera automat ca urmare a neluării în considerare a acesteia (v. mai sus).

Introducere date privind caracteristicile încărcărilor

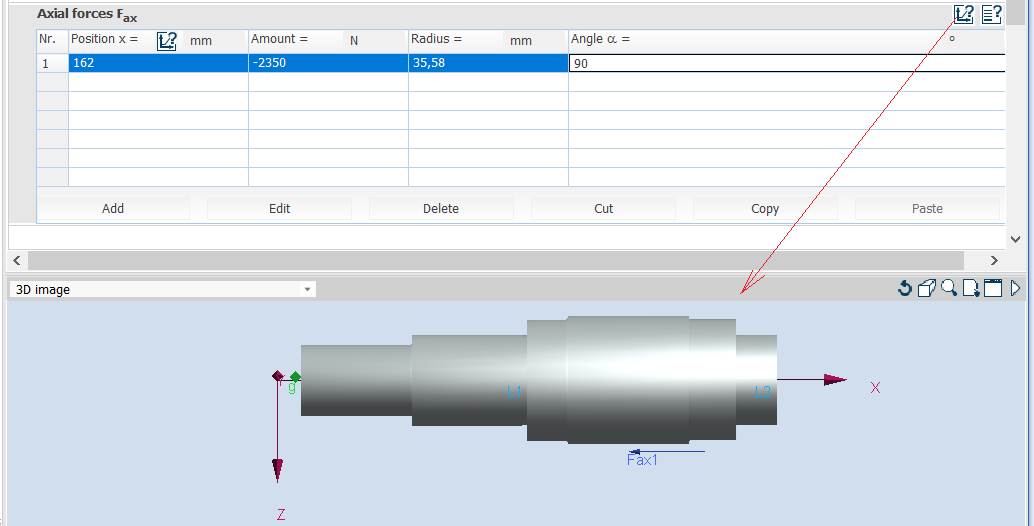
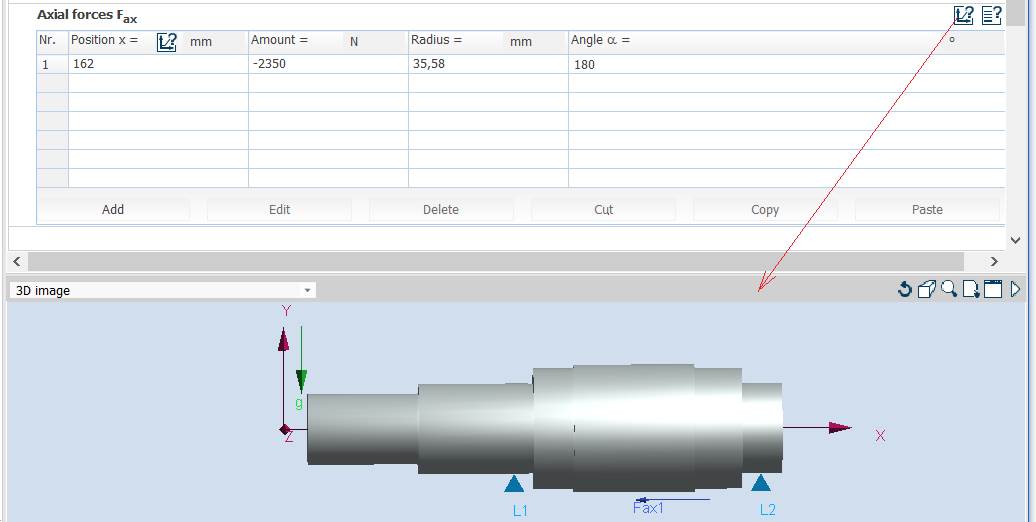
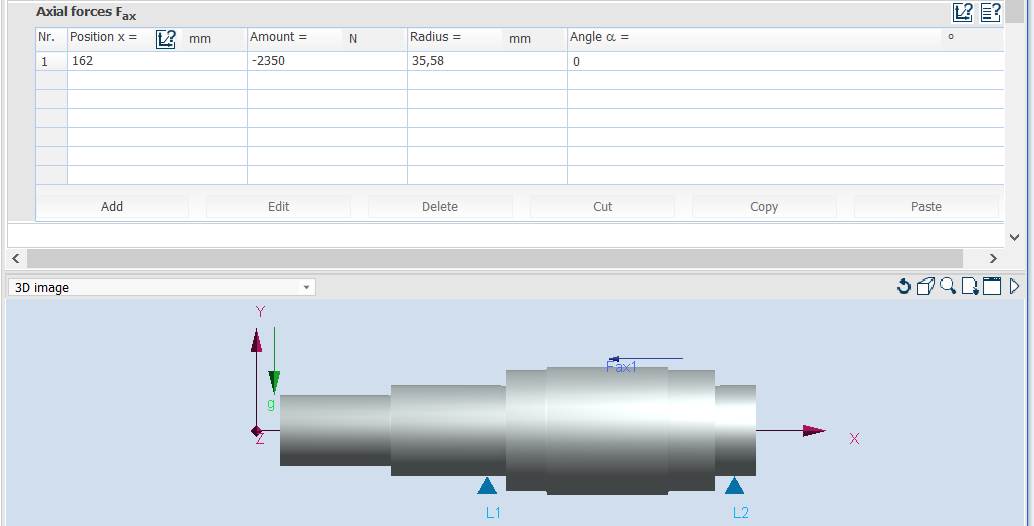
Introducere date despre încărcarea cu forțe axiale în Tabelul Axial Forces F_ax

- pentru arborele de intrare al RCil H:

: ¿, [se introduc valorile în casetele (poziția, la jumătatea danturii)], (valoarea, cu semnul -, opus axei x), (raza, distanța față de axa X), (unghiul în planul YZ, față de axa Y, v. Anexa.13.1.1).

\

- pentru arborele de intrare al RCil Vs:

: ¿, [se introduc valorile în casetele (poziția, la jumătatea danturii)], (valoarea, cu semnul -, opus axei x), (raza, distanța față de axa X), (unghiul în planul YZ, față de axa Y, v. Anexa.13.1.1).

- pentru arborele de intrare al RCil Vj:

: ¿, [se introduc valorile în casetele (poziția, la jumătatea danturii)], (valoarea, cu semnul -, opus axei x), (raza, distanța față de axa X), (unghiul în planul YZ, față de axa Y, v. Anexa.13.1.1).

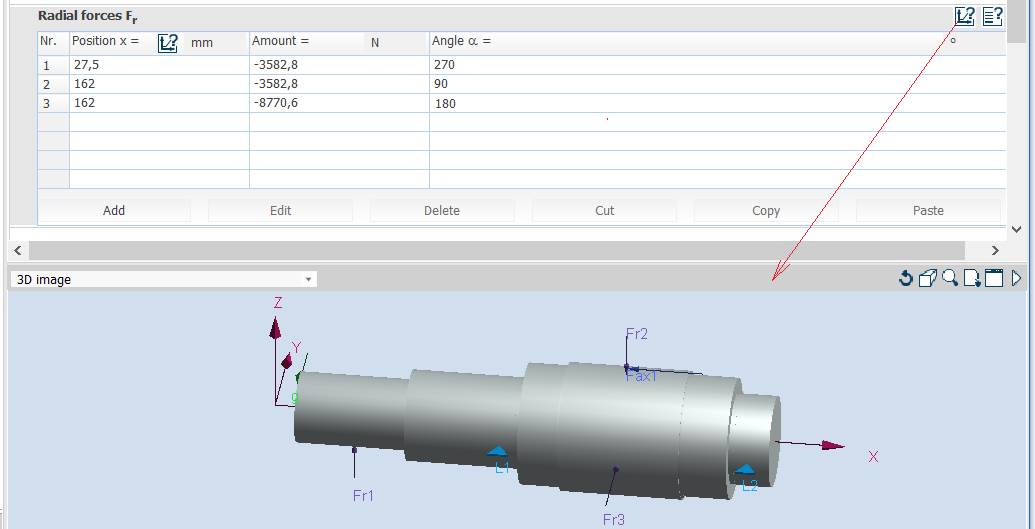
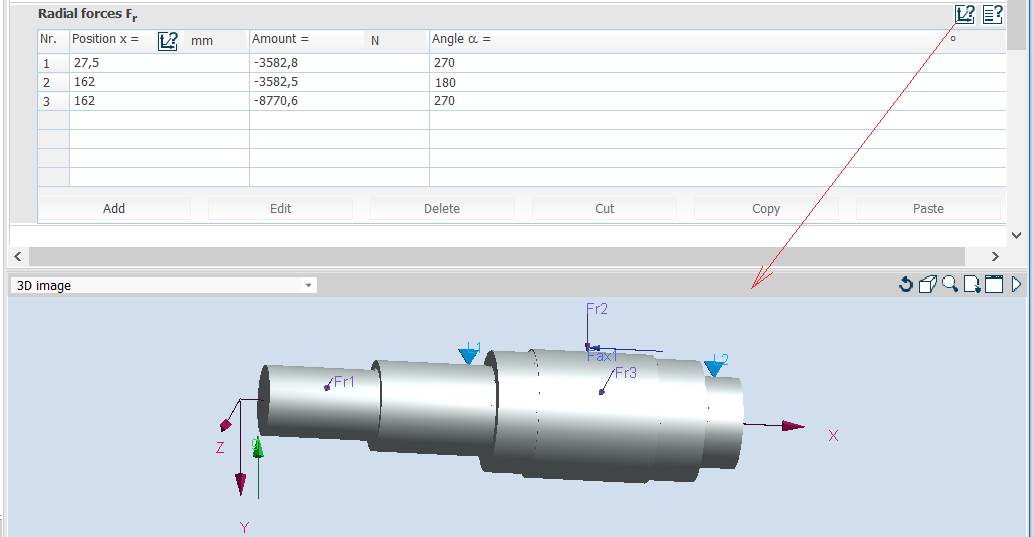
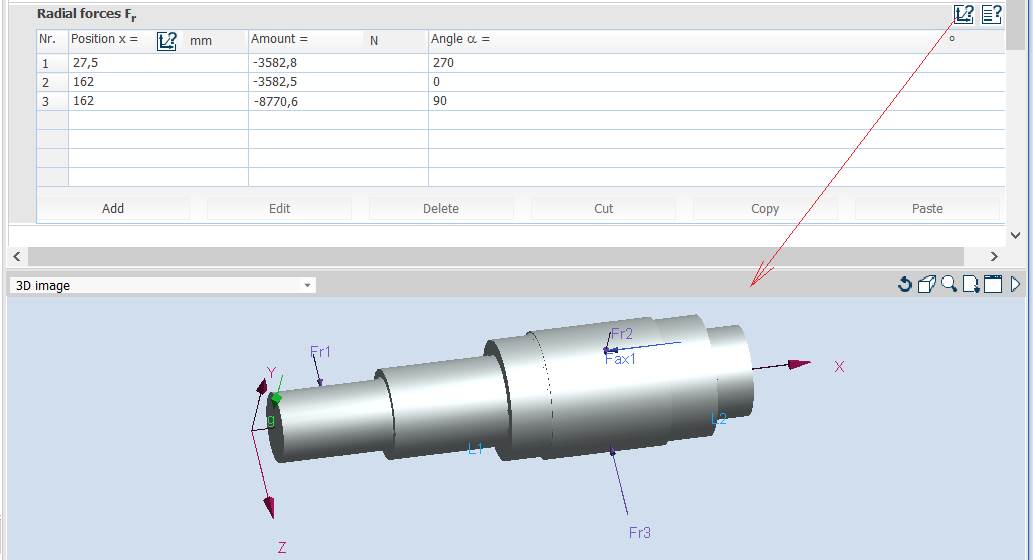
Introducere date despre încărcarea cu forțe radiale în tabelul Radial Forces F_r

- pentru arborele de intrare a RCil H:

: ¿, [se introduc valorile în casetele (poziția)], (valoarea, cu semnul -, opus axei x), (unghiul în planul YZ, față de axa Y, v. Anexa.13.1.1).

- pentru arborele de intrare al RCil Vs:

: ¿, [se introduc valorile în casetele (poziția)], (valoarea, cu semnul -, opus axei x), (unghiul în planul YZ, față de axa Y, v. Anexa.13.1.1).

- pentru arborele de intrare al RCil Vj:

: ¿, [se introduc valorile în casetele (poziția)], (valoarea, cu semnul -, opus axei x), (unghiul în planul YZ, față de axa Y, v. Anexa.13.1.1).

Introducere date despre încărcarea cu momente de încovoiere în tabelul Bending moments M_b

Obs. Pentru verificarea arborelui s-au considerat că forța axială acționează excentric (la nivelul cilindrului de rostogolire) și momentul de încovoiere va fi calculat de MDESIGN.

: ¿, [se introduc valorile în casetele (poziția), (valoarea momentului de torsiune) ] ® ¿ ® : ¿ (conducător) sau ¿ (condus), ¿.

, v. Anexa.13.1.1).

Introducere date despre încărcări, calculul la oboseală și coeficienți de siguranță

Introducere date despre material

¿ ® : [se va selecta linia cu materialul (18MoC…) ¿.

Verificare date de intrare

[se va selecta cu ¿ opțiunea ] ® ¿ și ¿

- pentru arborele de intrare a RCil H:

și

- pentru arborele de intrare a RCil Vs:

și

- pentru arborele de intrare a RCil Vj:

și

4. REZOLVAREA MODELULUI ȘI SALVAREA REZULTATELOR

¿

sau ¿ sau F10

®

Corectare neconcordanţe sau erori în datele de intrare (numai dacă apar ferestre de avertizare)

®

¿

sau ¿ sau F10

®

¿

®

Shaft.pdf

® ¿

5. REZULTATE Și VERIFICĂRI

5.1 Rezultate generale

Selectare pagina Output

Date generale despre arbore

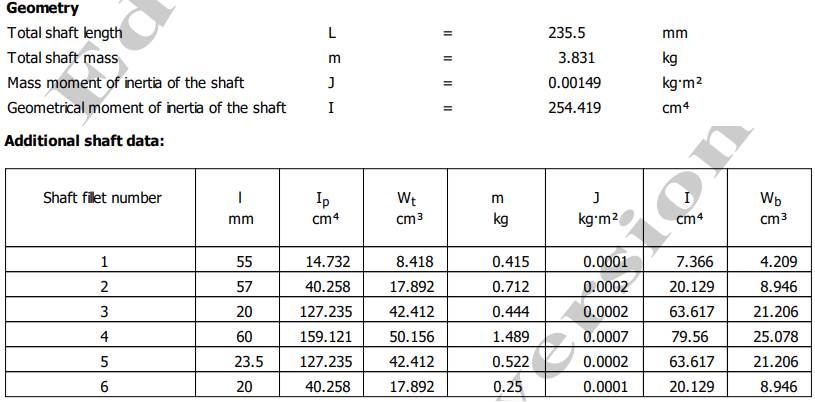
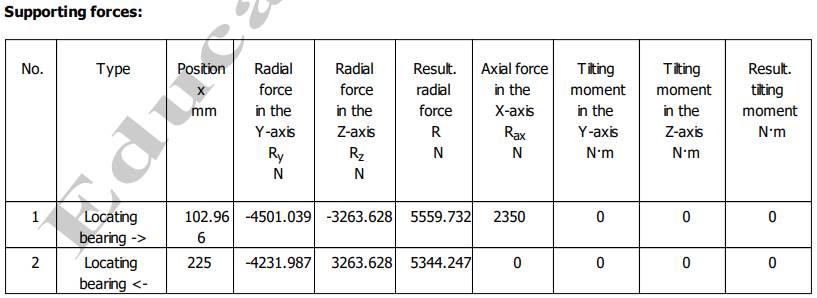
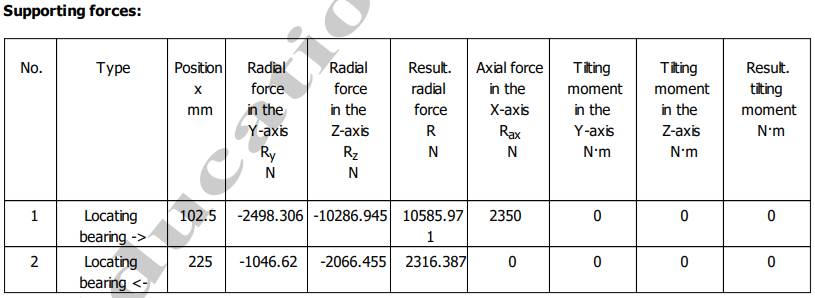
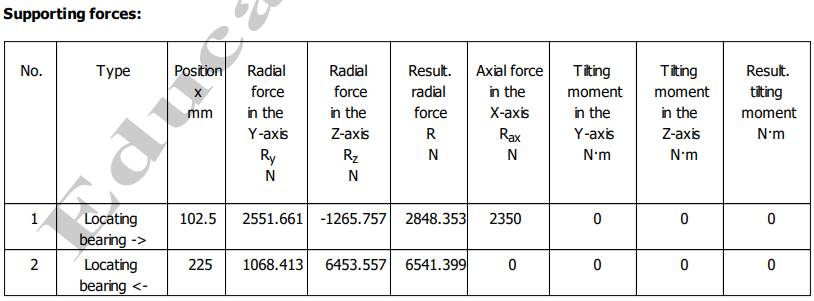
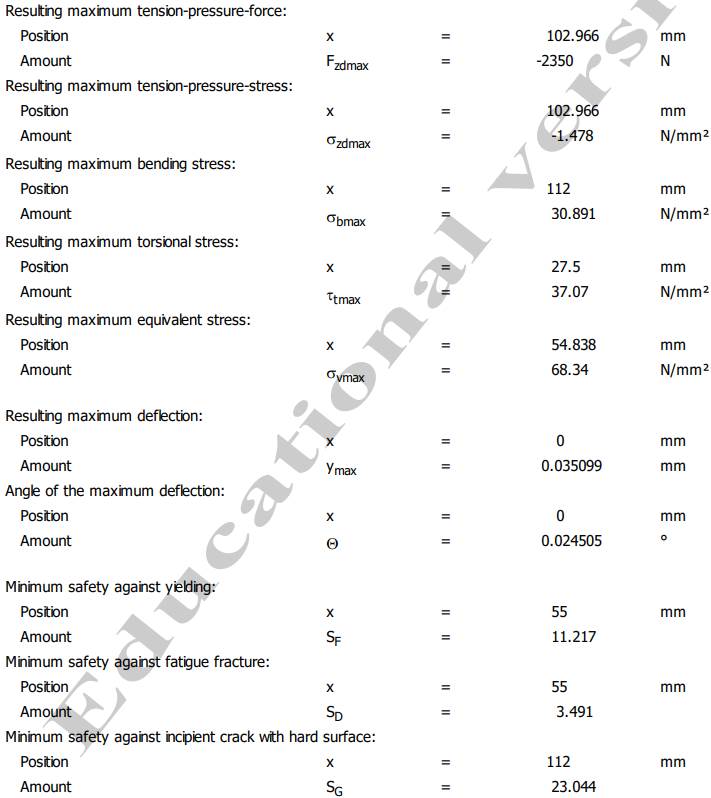
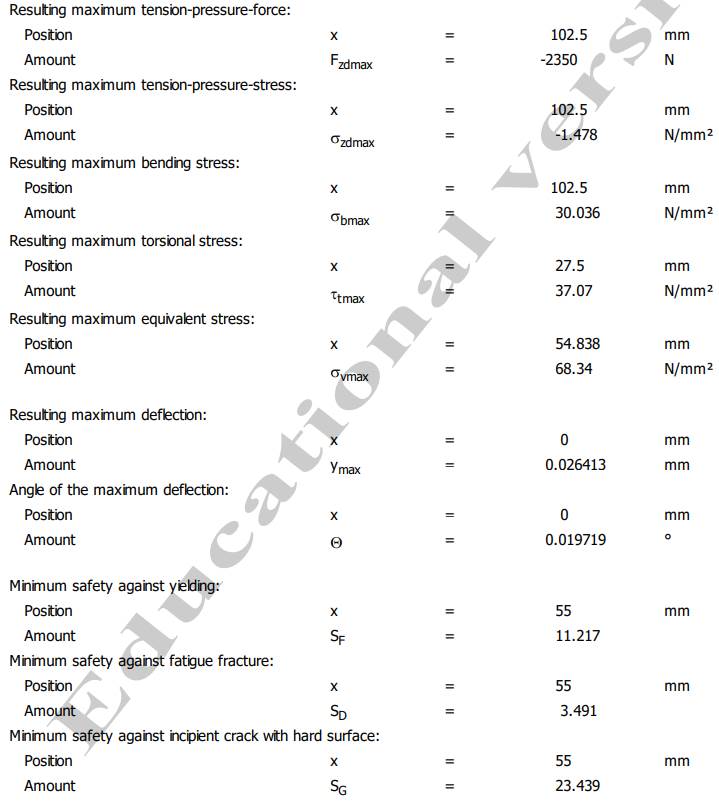
Semnificații: L - Total shaft length (lungimea totală a arborelui); m – Total shaft mass (masa totală a arborelui; J – Mass moment of inertia of the shaft (momentul de inerție masic al arborelui), I – Geometrical moment of inertia of the shaft (momentul de inerție geometric); x_s – Position of the centre of gravity in the X-axis (poziția centrului de greutate pe axa X), I_p – momentul de inerie polar, W_t – momentul static, W_t – modulul de rezistență axial.

Valorile reacțiunilor din reazeme (lagăre cu rulmenți)

- pentru arborele de intrare al RCil H:

- pentru arborele de intrare al RCil Vs:

- pentru arborele de intrare al RCil Vj:

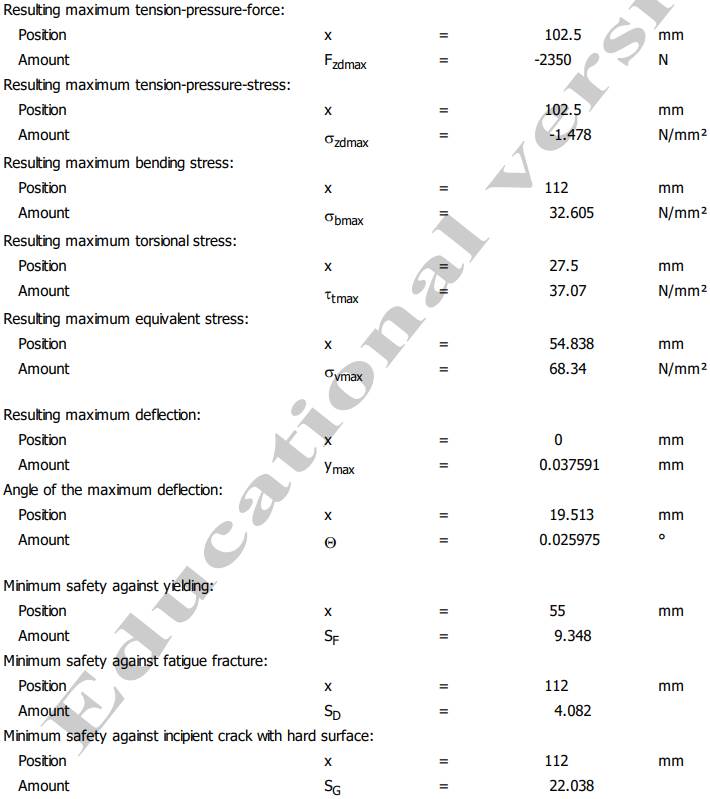
Obs. Valorile forțelor de reacțiune R (rezultanta) se folosesc pentru calculul rulmenților (v. Subcap.14.1)

Valorile extreme (maxime sau minime) ale parametrilor de verificare

- pentru arborele de intrare al RCil H:

- pentru arborele de intrare al RCil Vs:

- pentru arborele de intrare al RCil Vj:

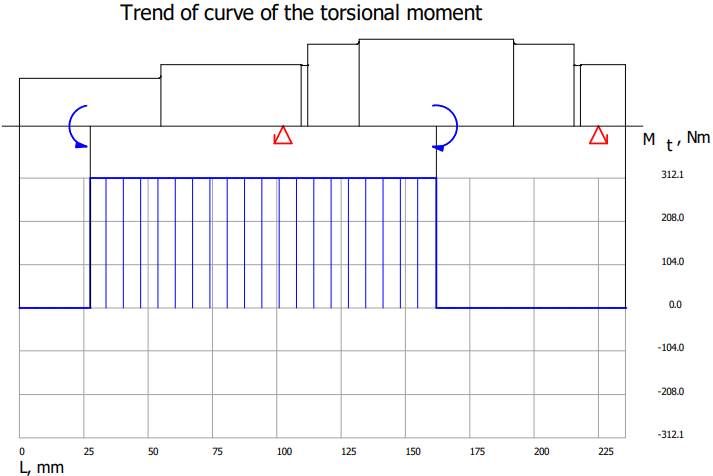
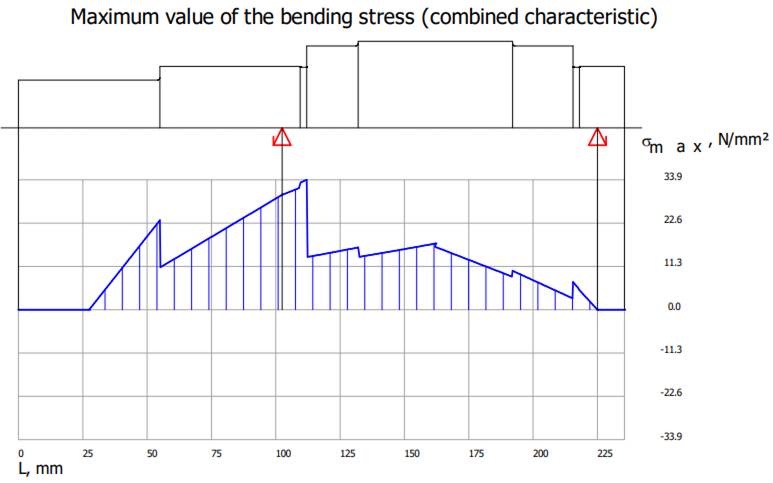
Semnificații: M_bmax – Resulting maximum bending moment ( momentul maxim de încovoiere rezultant), M_tmax – Resulting maximum torsional moment (momentul maxim de torsiune rezultant), F_zdmax - Resulting maximum tension-pressure force (forța de tracțiune-compresiune maximă rezultantă), σ_zdmax - Resulting maximum tension-pressure stress (tensiunea de tracțiune-compresiune maximă rezultantă), σ_bmax – Resulting maximum bending stress ( tensiunea maximă de încovoiere rezultantă), τ_tmax – Resulting maximum torsional stress (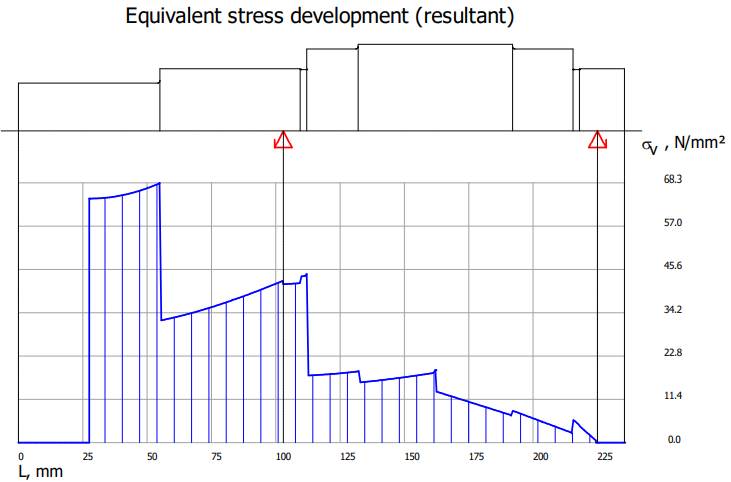tensiunea maximă de torsiune rezultantă), σ_vmax – Resulting maximum equivalent stress (tensiunea maximă echivalentă), y_max – 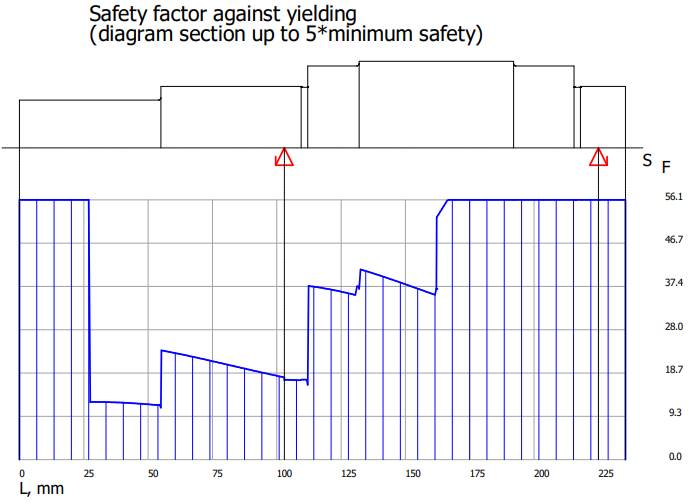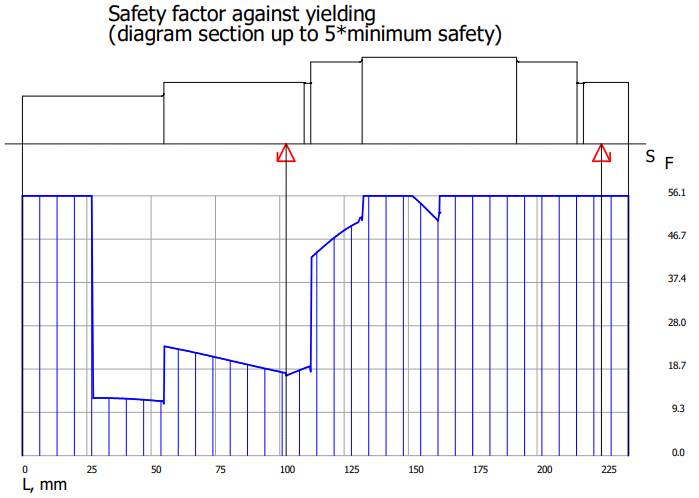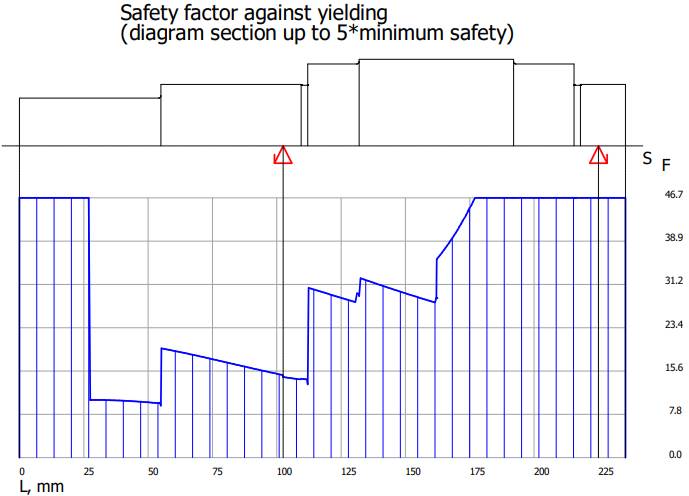Resulting maximum deflection (săgeata maximă la încovoiere), Θ – Angle of the maximum deflection (rotirea maximă la încovoiere), S_F – Minimum safty against yielding (coeficientul de siguranță minim la curgere), S_D – Minimum safty against fatigue fracture (coeficientul de siguranță minim la rupere prin oboseală), S_G – Minimum safty against incipient crack with hard surface (coeficientul de siguranță minim de inițiere a fisurii pe suprafețe 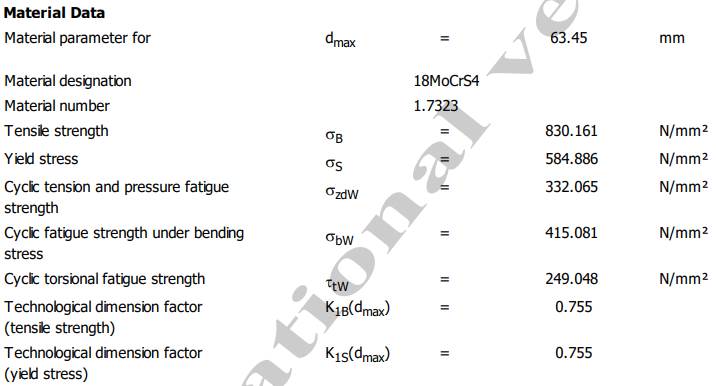durerificate).

Date despre material

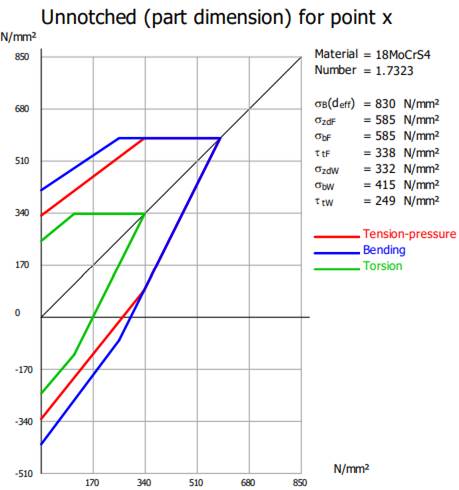
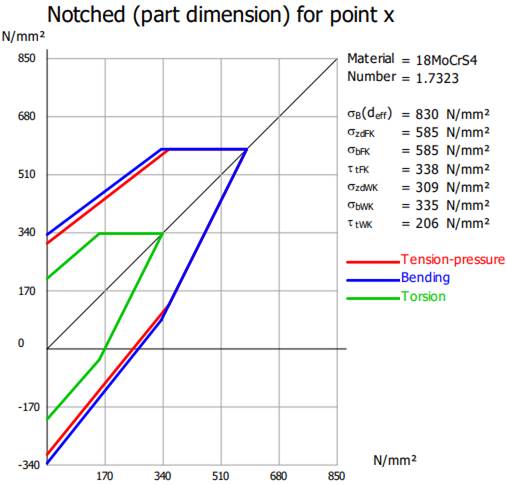
Semnificații: d_max – Material parameter for (diametrul maxim pentru parametri de material), Material desigantion (materialul adoptat), Material number (codul materialului), σ_B – Tensile strength (rezistența la tracțiune), σ_S – Yield strength (rezistența la curgere), σ_zdW – Cyclic tension and pressure fatigue (rezistența la oboseală pentru tracțiune-compresiune), σ_bW – Cyclic fatigue strength under bending stress (rezistența la oboseală pentru încovoiere), τ_tW – Cyclic torsional fatigue strength (rezistența la oboseală pentru torsiune), K_1B(d_max) – Technological dimension factor (tensile strength) (factorul dimensional tehnologic pentru rezistența la tracțiune), K_1S(d_max) – Technological dimension factor (yield strength) (factorul dimensional tehnologic pentru rezistența la curgere)

5.2. Verificare la solicitări compuse (încovoiere + torsiune)

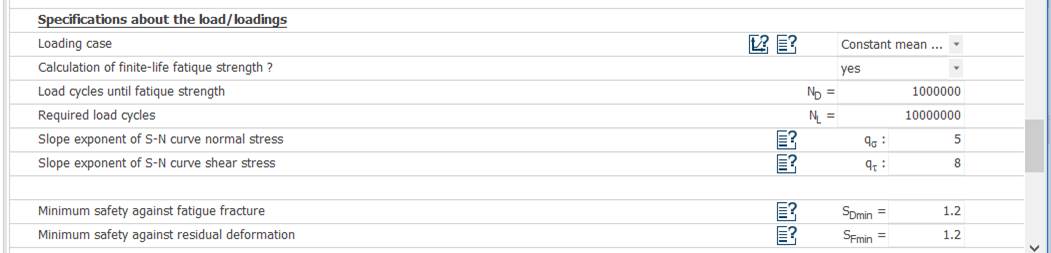
Calculului de verificare la solicitări compuse se face cu scopul evitării deformării plastice remanente în direcție radială a arborelui.

Verificarea la solicitări compuse se face cu relația,

σ_vmax ≤ σ_a,

în care, σ_vmax reprezintă tensiunea echivalentă maximă (v. subcap. 5.2.1, 5.2.2, 5.2.3, 5.2.4), σ_a = σ_S/S_F cu σ_S, rezistența la curgere și S_F, coeficientul de siguranță de rezistență admisibil (minim) la deformare plastică (s-a introdus ca dată de intrarea S_F = 1,2).

Valoarea rezistenței la curgere, σ_S = 584,886 MPa, pentru materialul ales este indicată în grupul Material Data (v. subcap. 5.1).

Din inegalitatea de mai sus se determină a doua relație de verificare la solicitări compuse,

S_Fmin ≥ S_F,

în care S_Fmin = σ_vmax/σ_S este coeficientul de siguranță minim, obținut prin calcul.

Obs. Dacă verificarea nu este îndeplinită se impune mărirea diametrelor tronsoanelor acestuia sau realegerea unui material cu performanţe mai bune

5.2.1 Verificare la solicitări compuse a arborlelui de intrare al RCil H

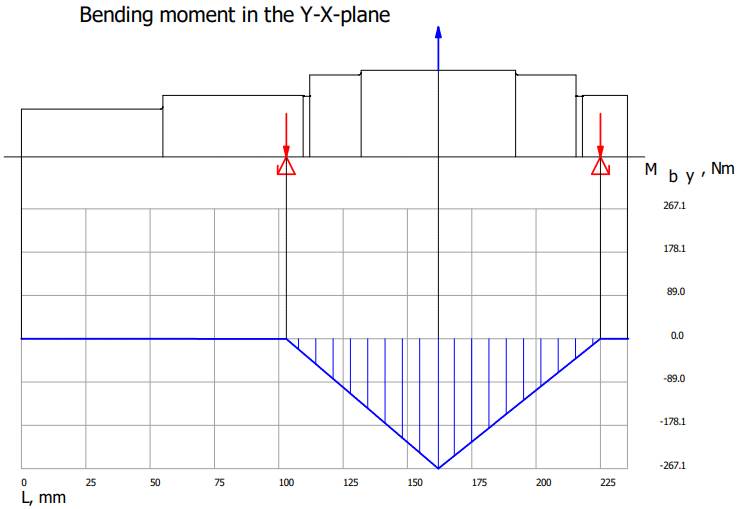
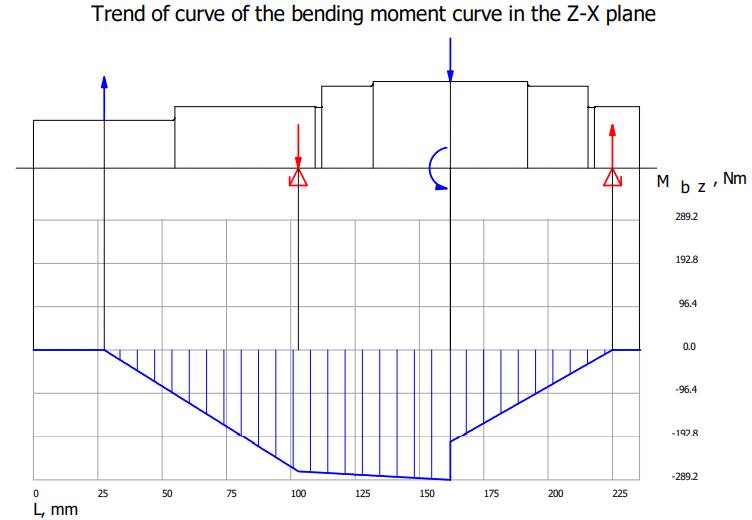
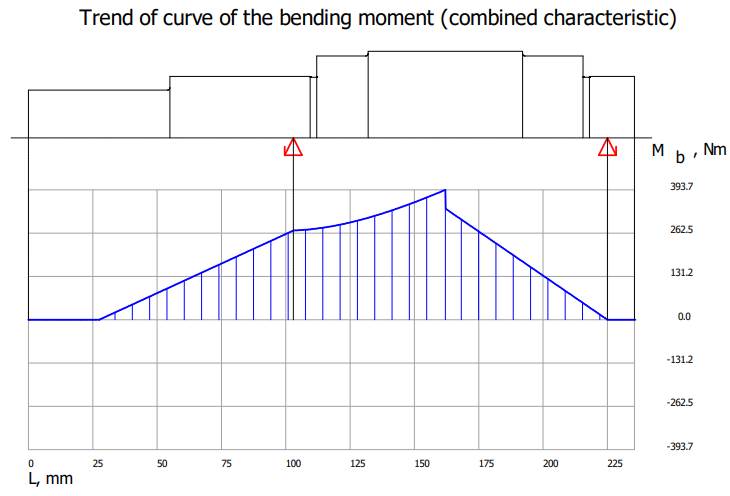
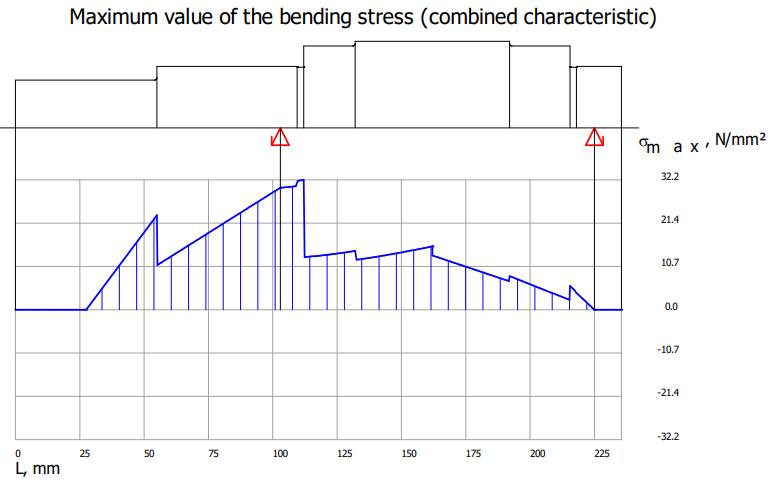
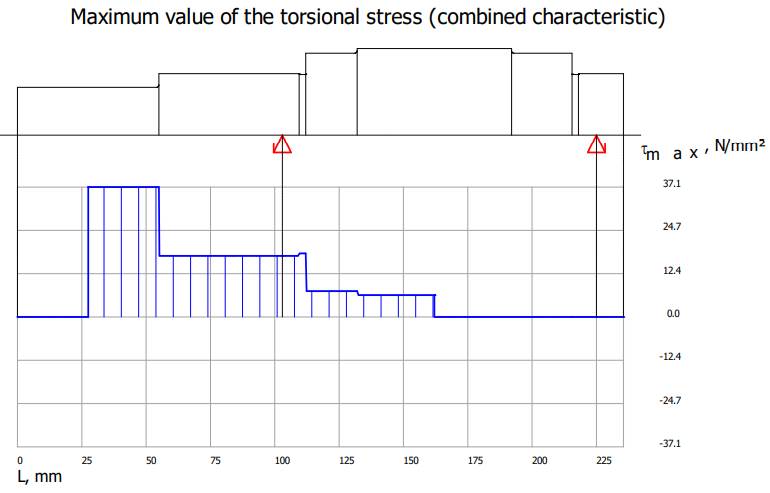
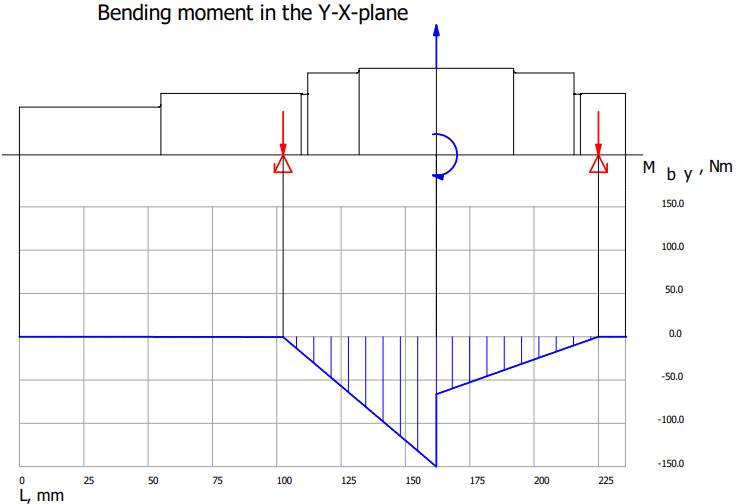
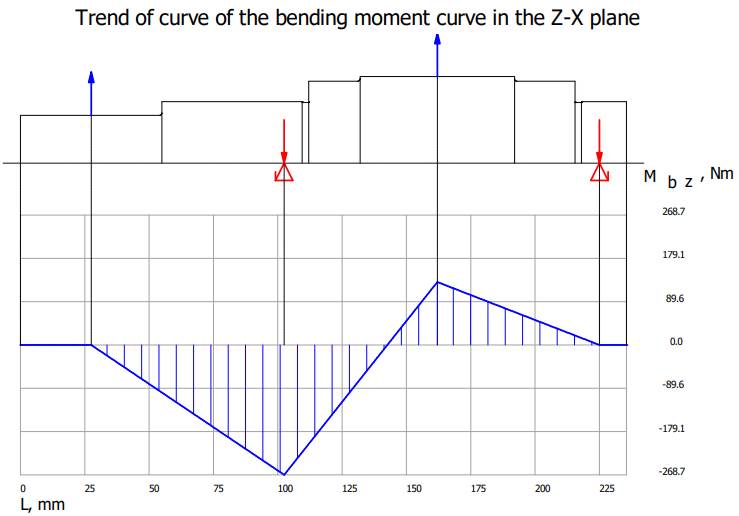
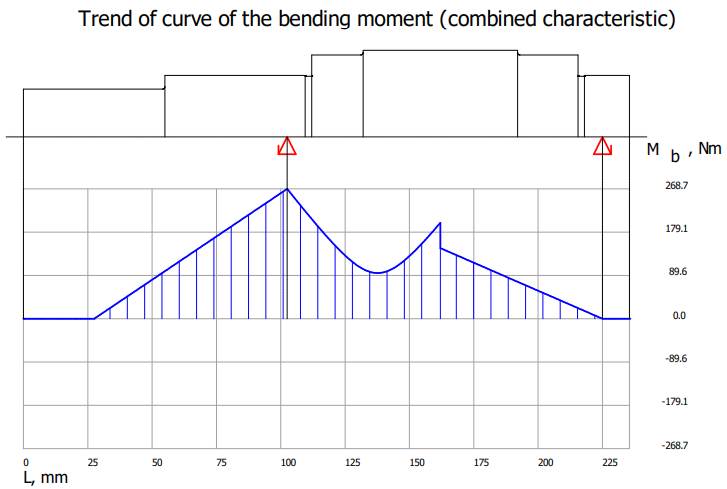
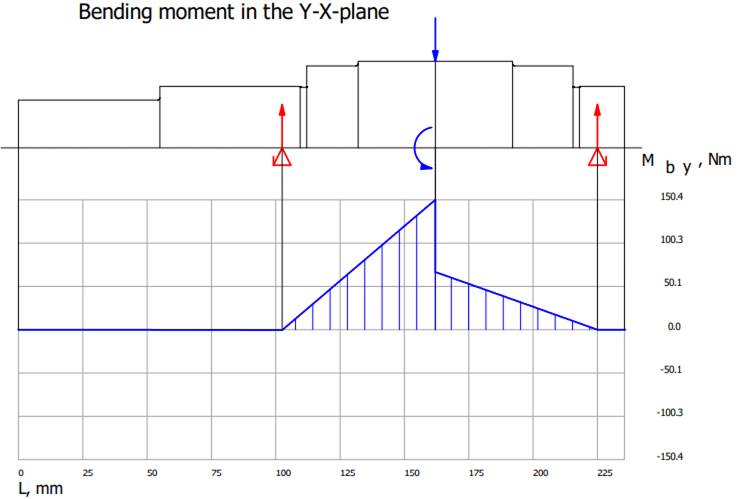
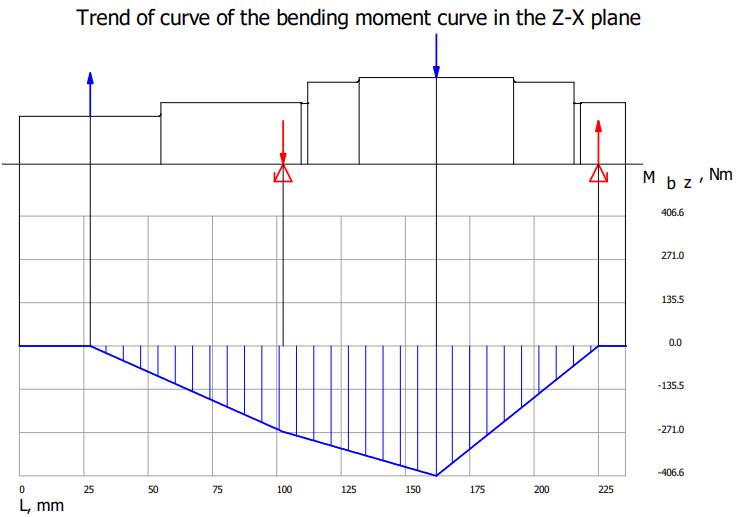
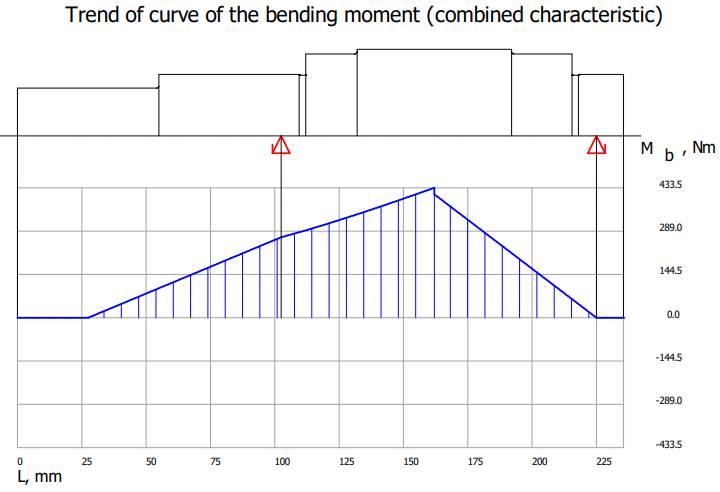
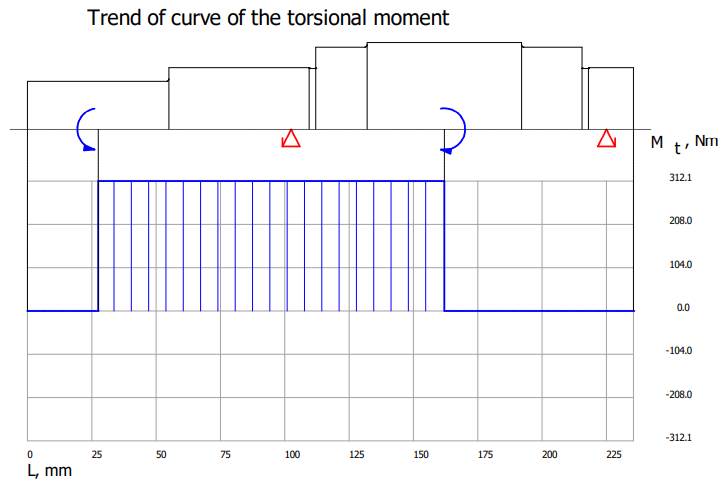
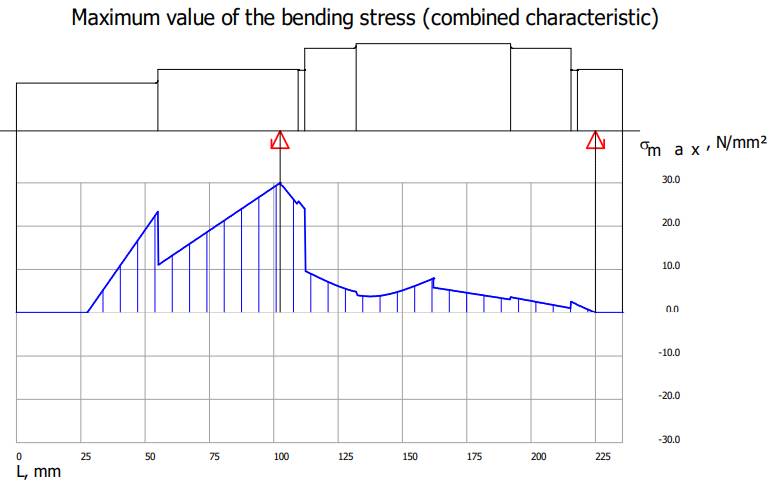
Valorile momentelor de încovoiere și de torsiune

Diagrama momentelor de încovoiere în planul YX

Diagrama momentelor de încovoiere în planul ZX

Diagrama momentelor de încovoiere rezultante

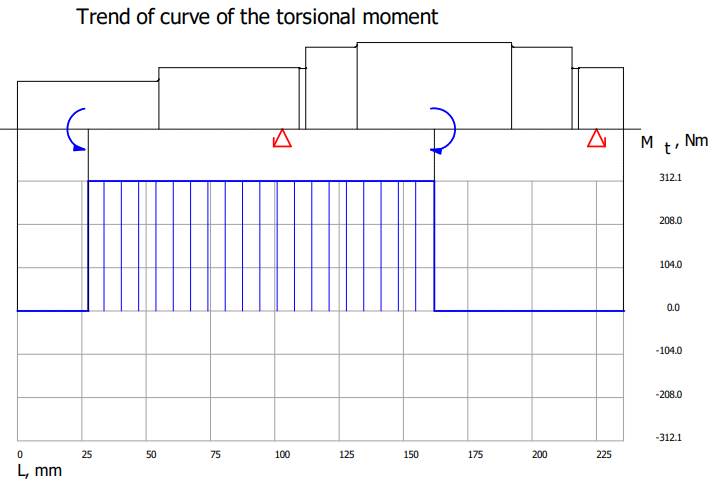
Diagrama momentelor de torsiune

Valorile tensiunilor de încovoiere, de torsiune și echivalente

Diagrama tensiunilor de încovoiere rezultante

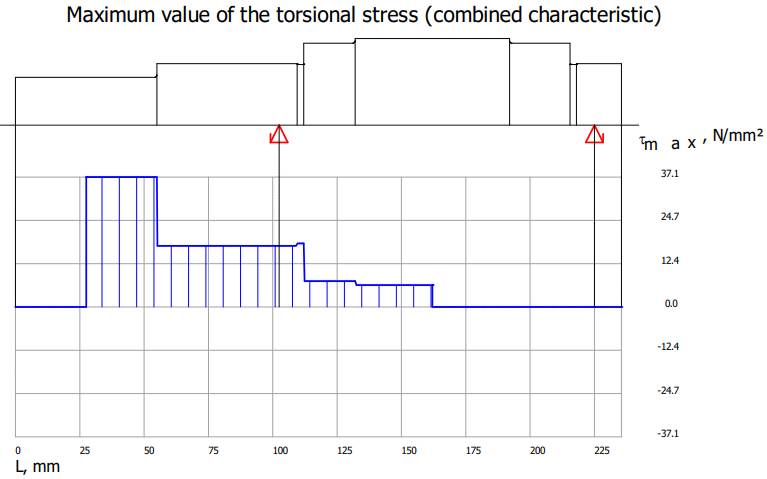
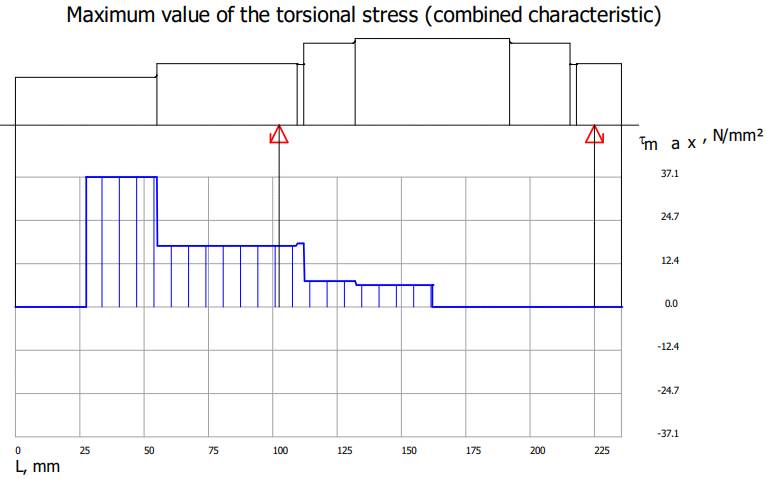
Diagrama tensiunilor de torsiune

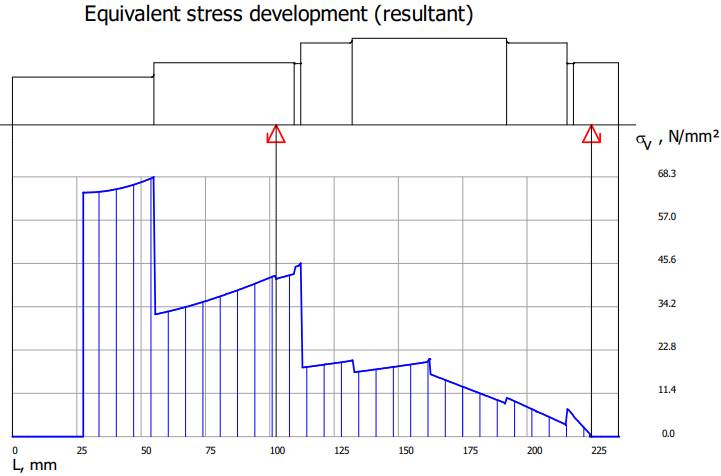
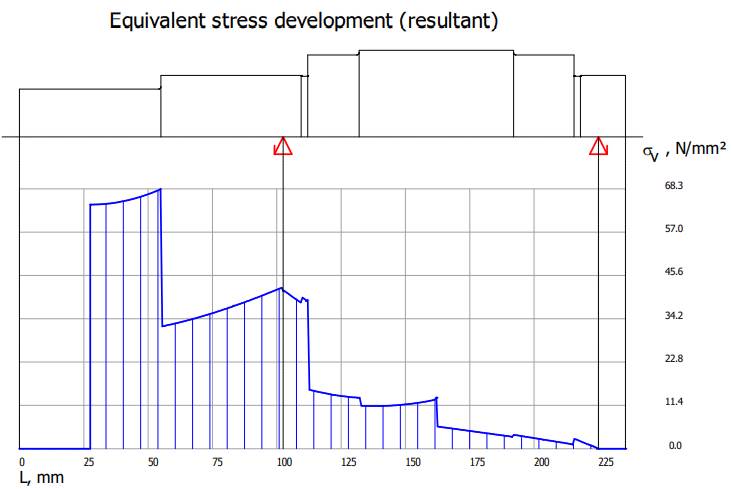
Diagrama tensiunilor echivalente

Diagrama coeficientului de siguranță la curgere

Verificarea arborelui la solicitări compuse

S_Fmin ≥ S_F cu S_Fmin = 11,217; 11,217 > 1,2 (se verifică)

5.2.2 Verificare la solicitări compuse a arborelui de intrare a RCil Vs

Valorile momentelor de încovoiere și de torsiune

Diagrama momentelor de încovoiere în planul YX

Diagrama momentelor de încovoiere în planul ZX

Diagrama momentelor de încovoiere rezultante

Diagrama momentelor de torsiune

Valorile tensiunilor de încovoiere, de torsiune și echivalente

Diagrama tensiunilor de încovoiere rezultante

Diagrama tensiunilor de torsiune

Diagrama tensiunilor echivalente

Diagrama coeficientului de siguranță la curgere

Verificarea arborelui la solicitări compuse

S_Fmin ≥ S_F cu S_Fmin = 11,217; 11,217 > 1,2 (se verifică)

5.2.3 Verificare la solicitări compuse a arborelui de intrare a RCil Vj

Valorile momentelor de încovoiere și de torsiune

Diagrama momentelor de încovoiere în planul YX

Diagrama momentelor de încovoiere în planul ZX

Diagrama momentelor de încovoiere rezultante

Diagrama momentelor de torsiune

Valorile tensiunilor de încovoiere, de torsiune și echivalente

Diagrama tensiunilor de încovoiere rezultante

Diagrama tensiunilor de torsiune

Diagrama tensiunilor echivalente

Diagrama coeficientului de siguranță la curgere

Verificarea arborelui la solicitări compuse

S_Fmin ≥ S_F cu S_Fmin = 9,348; 9,348 > 1,2 (se verifică)

5.3 Verificare la deformații (rigiditate)

5.3.1 Verificare la deformații de încovoiere (flexionale)

Calculul deformaţiilor flexionale, în general, se efectuează cu scopul preîntâmpinării funcţionărilor necorespunzătoare (cu vibraţii transversale şi zgomote) ale elementelor susţinute (în special, roţi dinţate) şi a lagărelor cu rulmenți.

Calculul la deformaţii de încovoiere (de verificare) constă în determinarea valorilor săgeţilor sub organele susţinute (roţi dinţate) şi a deformaţiilor unghiulare (rotirilor) în lagăre şi limitarea acestora la valori admisibile:

y_max  ≤  y_a,

Θ_max ≤  Θ_a.

Valorile admisibile ale deformaţiilor de încovoiere, recomandate în literatura de specialitate, sunt:

- pentru săgeţile de sub roţile dinţate montate pe arbore, y_a ≤ (0,01 ... 0,03)m_n, m_n fiind modulul normal al danturii angrenajului, în mm;

- pentru deformaţiile unghiulare, în radiani: Θ_a = 8.10^-3 – pentru lagăre cu rulmenţi radiali cu bile; Θ_a  = 2,5.10^-3 – pentru lagăre cu rulmenţi radiali cu role cilindrice; Θ_a = 1,7.10^-3 – pentru lagăre cu rulmenţi radial-axiali cu bile sau cu role conice; Θ_a=5.10^-2

- pentru lagăre cu rulmenţi radial oscilanţi cu bile sau cu role butoi pe două rînduri; Θ_a  = 10^-3 – pentru lagăre cu alunecare;

- pentru arborii reductoarelor de turație se recomandă, y_a = (2…3) 10^-4 L, unde L este distanța dintre reazeme (lagăre).

Obs. Dacă deformaţiile efective nu sunt mai mici decât cele recomandate în literatura de specialitate (nu sunt îndeplinite condiţiile de verificare), se măreşte rigiditatea arborelui la încovoiere, prin mărirea diametrelor tronsoanelor acestuia

5.3.1.1 Verificare la deformații a arborlelui de intrare al RCil H

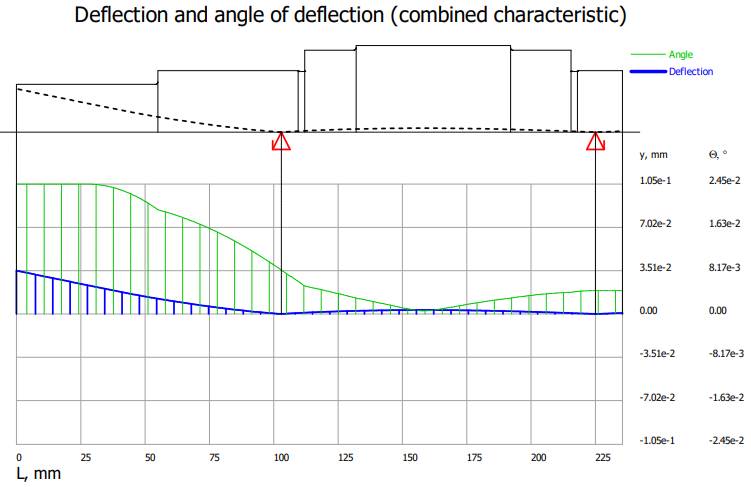
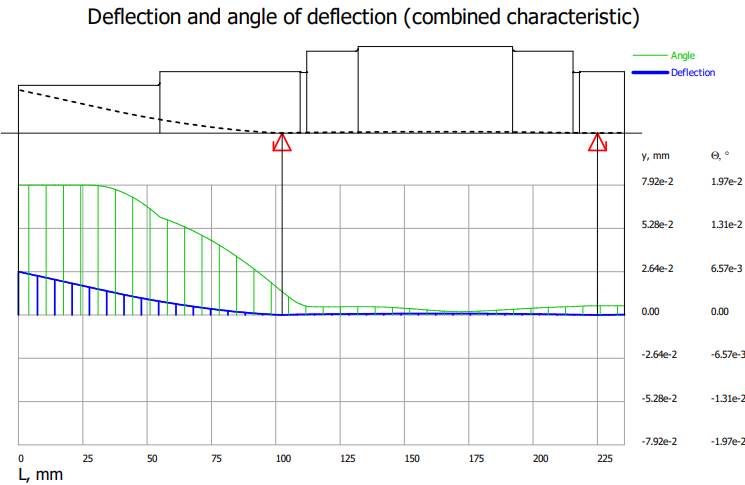
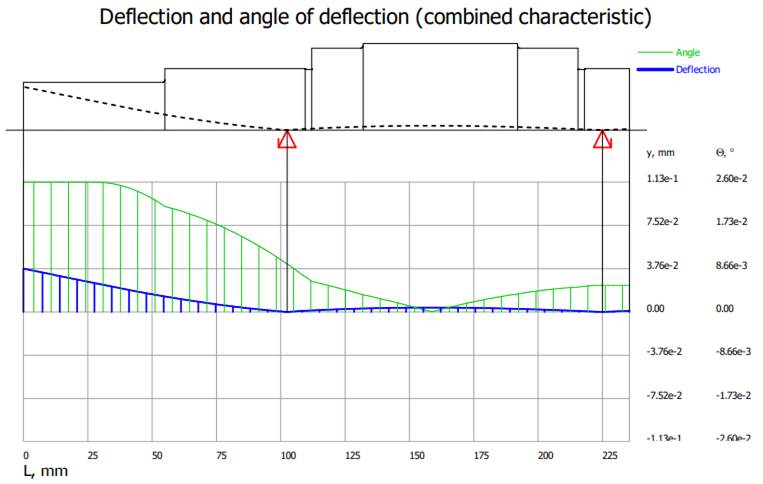
Diagramele săgeților și rotirilor

Valorile săgeților și rotirilor maxime

Valorile săgeților și rotirilor la jumătatea tronsonului cu dantura (x = 142 mm)

Verificarea arborelui la deformații flexionale

- verificarea la deformații liniare (săgeți) în zona angrenajului, y_x  ≤  y_a; y_a = (0,01…0,03) * 4 = 0,04…0,12 mm;

0,002933 < 0,04…0,12 mm (se verifică)

- verificarea la deformații liniare (săgeți) maxime: y_max  ≤  y_a; y_a = 2,5 * 10^-4 * 181 = 0,0452 mm;

0,035099 < 0,0452 mm (se verifică);

- verificare la deformații unghiulare (rotiri) maxime în lagăre: Θ_max ≤  Θ_a; θ_a = 1,7.10^-3 rad = 1,7.10^-3 180/π = 0,97^o;

0,0024505 < 0,97 ^o (se verifică)

5.3.1.2 Verificare la deformații a arborlelui de intrare al RCil Vs

Diagramele săgeților și rotirilor

Valorile săgeților și rotirilor maxime

Valorile săgeților și rotirilor la jumătatea tronsonului cu dantura (x = 142 mm)

Verificarea arborelui la deformații flexionale

- verificarea la deformații liniare (săgeți) în zona angrenajului, y_x  ≤  y_a; y_a = (0,01…0,03) * 4 = 0,04…0,12 mm;

0,00075 < 0,04…0,12 mm (se verifică)

- verificarea la deformații liniare (săgeți) maxime: y_max  ≤  y_a; y_a = 2,5 * 10^-4 * 181 = 0,0452 mm;

0,026413 < 0,0452 mm (se verifică);

- verificare la deformații unghiulare (rotiri) maxime în lagăre: Θ_max ≤  Θ_a; θ_a = 1,7.10^-3 rad = 1,7.10^-3 180/π = 0,97^o;

0,019719 < 0,97 ^o (se verifică)

5.3.1.3 Verificare la deformații a arborlelui de intrare al RCil Vj

Diagramele săgeților și rotirilor

Valorile săgeților și rotirilor maxime

Valorile săgeților și rotirilor la jumătatea tronsonului cu dantura (x = 142 mm)

Verificarea arborelui la deformații flexionale

- verificarea la deformații liniare (săgeți) în zona angrenajului, y_x  ≤  y_a; y_a = (0,01…0,03) * 4 = 0,04…0,12 mm;

0,003485 < 0,04…0,12 mm (se verifică)

- verificarea la deformații liniare (săgeți) maxime: y_max  ≤  y_a; y_a = 2,5 * 10^-4 * 181 = 0,0452 mm;

0,037591 < 0,0452 mm (se verifică);

- verificare la deformații unghiulare (rotiri) maxime în lagăre: Θ_max ≤  Θ_a; θ_a = 1,7.10^-3 rad = 1,7.10^-3 180/π = 0,97^o;

0,025975 < 0,97 ^o (se verifică)

5.3.2 Verificare la deformații torsionale (de răsucire)

Calculul de verificare la deformaţii de torsiune (răsucire)

Acest calcul presupune determinarea valorilor unghiurilor de răsucire  (rotirilor axiale) ale arborelui şi limitarea acestora la valori admisibile,

φ  ≤  φ_a.

Valorile admisibile pentru unghiul de torsiune (răsucire), determinate de destinaţia arborelui, recomandate în literatura de specialitate, sunt:  φ_a = (15 ... 25) . 10^-2 rad/m, pentru arborii diferenţialelor autovehiculelor (arborii planetari);  φ_a = (40 ... 55) 10^-4 rad/m, pentru arborii mecanismelor de deplasare ale podurilor rulante. În cazul arborilor scurţi  (reductoare de uz general, cutii de viteze etc.), în general, rigiditatea la torsiune nu are rol esenţial şi, ca urmare, pentru calculul la deformaţii torsionale se poate considera, φ_a = (25 ... 50) 10^-4 rad/m.

Obs. În cazul în care unghiurile efective de  torsiune (răsucire) depăşesc valorile recomandate în literatura de specialitate, se măreşte rigiditatea arborelui la torsiune, prin mărirea diametrelor tronsoanelor acestuia.

Verificarea arborelui la deformații torsionale

Considerând unghiul de rotire calculat,

,

rezultă: 0,015  ≤  (25…50) . 10^-4 180/π; 0,015  ≤  0,14 …2,8 ^o/m (se verifică)

5.4 Verificare la solicitări variabile (oboseală)

Calculul la solicitări variabile (oboseală), în general, se efectuează în vederea preîntâmpinării ruperii arborilor prin oboseală (fisurare), cu precădere, în zona concentratorilor de tensiune (Anexa.13.1.2).

Condiţia rezistenţei la oboseală a arborilor drepţi în zonele care există concentratori de tensiuni (canale de pană, caneluri, salturi de diametre, găuri transversale, filet, ajustaje presate etc.), cu precădere, supuşi la solicitări compuse (torsiune şi încovoiere) este dată de relaţia,

S_Dmin ≥ S_D,    

în care S_Dmin, reprezintă coeficientul de siguranță minim, obținut prin calcul, și S_D coeficientul de siguranță admisibil (s-a introdus ca dată de intrarea S_D = 1,2).           

Obs. Dacă nu se verifică la oboseală se pot modifica zonele concentratorilor de tensiune (Anexa.13.1.3)

5.4.1 Verificare la solicitări variabile (oboseală) a arborlelui de intrare al RCil H

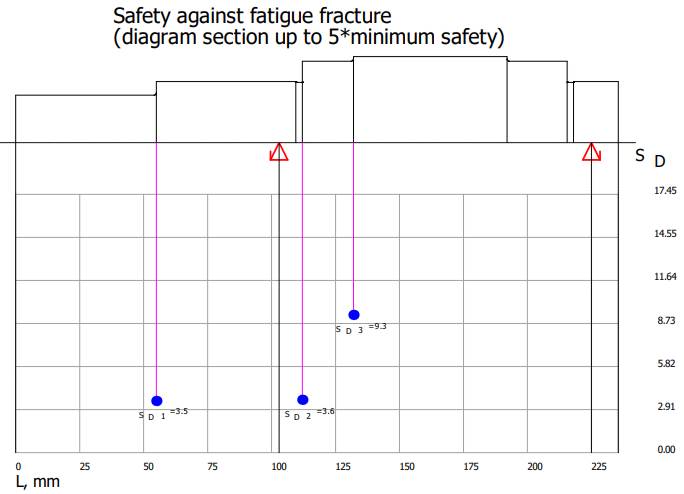
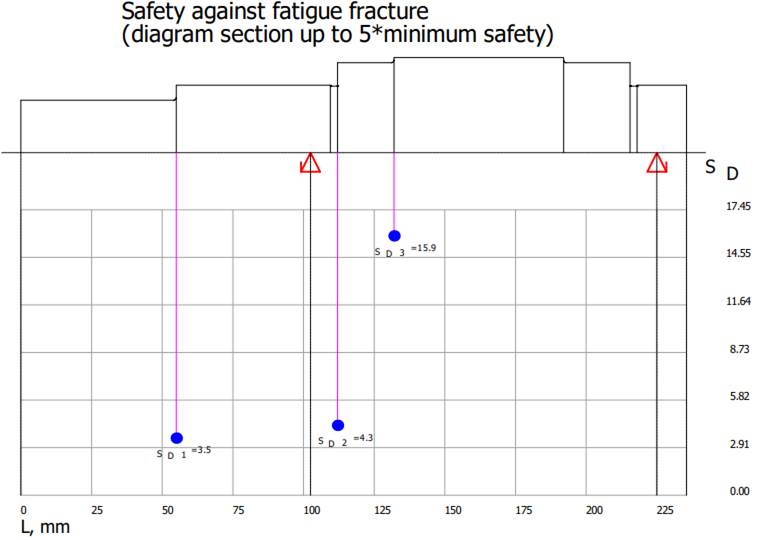
Diagrama coeficientului de siguranță la oboseală

Verificarea arborelui la solicitări variabile (oboseală)

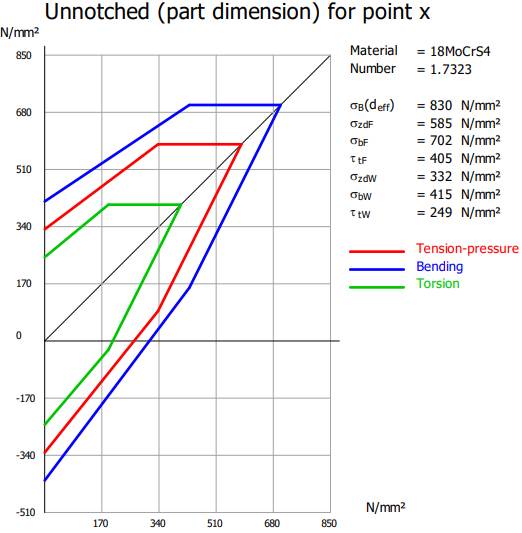
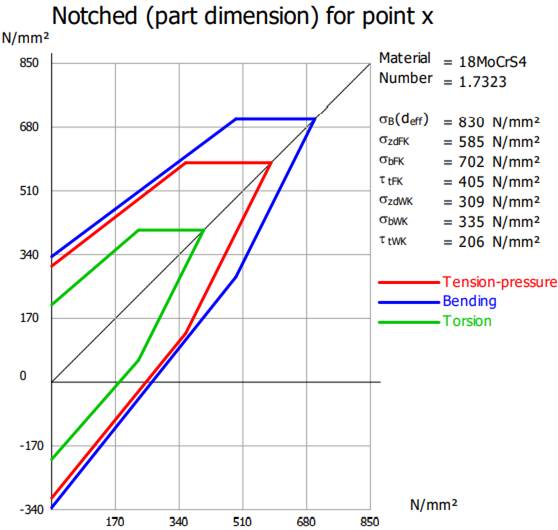
S_Dmin ≥ S_D: 3,491 > 1,2 (se verifică).

Diagramele Smith asociate zonei danturate fără/cu luarea în considerare a concentratorului de tensiune

5.4.2 Verificare la solicitări variabile (oboseală) a arborlelui de intrare al RCil Vs

Diagrama coeficientului de siguranță la oboseală

Verificarea arborelui la solicitări variabile (oboseală)

S_Dmin ≥ S_D: 3,491 > 1,2 (se verifică).

Diagramele Smith asociate zonei danturate fără/cu luarea în considerare a concentratorului de tensiune

5.4.3 Verificare la solicitări variabile (oboseală) a arborlelui de intrare al RCil Vj

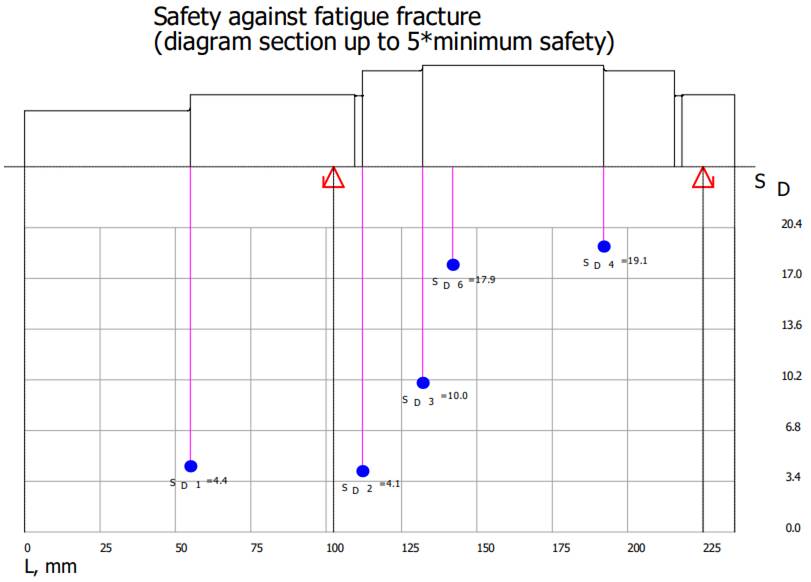
Diagrama coeficientului de siguranță la oboseală

Verificarea arborelui la solicitări variabile (oboseală)

S_Dmin ≥ S_D: 4,082 > 1,2 (se verifică).

Diagramele Smith asociate zonei danturate fără/cu luarea în considerare a concentratorului de tensiune

5.5 Verificare la vibrații

Calculul de verificare la vibraţii

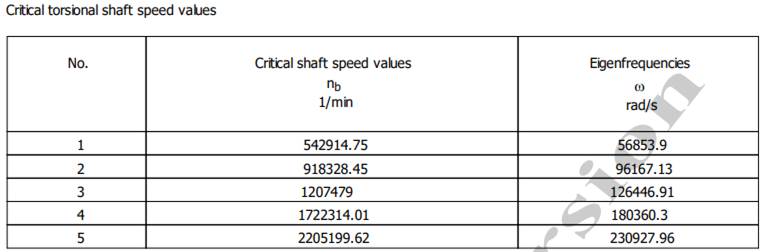
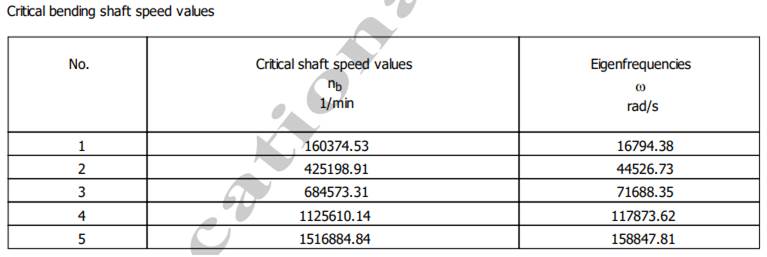
Scopul calculului de verificare la vibraţii este prevenirea ruperii arborelui din cauza eforturilor mult mărite care apar la intrarea în rezonanţă subansamblului acestuia. Calculul  constă în determinarea turaţiei critice a arborelui şi compararea acestuia cu turaţia de funcţionare.

Turaţia critică este turaţia la care arborele intră în rezonanţă ca urmare a situaţiei în care frecvenţa (pulsaţia) proprie coincide sau este multiplu al frecvenţei forţelor perturbatoare.

Frecvenţa (pulsaţia) proprie este o caracteristică a unui sistem oscilant independent de condiţiile iniţiale ale mişcării.

Verificarea la vibrații se face cu relația,

(0…n) ≠ (0,8…1,2) f₀,

unde, f₀ reprezintă prima frecvență proprie, n - turaţia.

Turațiile și vitezele unghiulare critice torsionale

Turațiile și vitezele unghiulare critice flexionale (de încovoiere)

Verificarea la vibrații

- torsionale, (0…n) ≠ (0,8…1,2)f₀;

(0…625) ≠ (0,8…1,2) 542914,75;

(0…625) ≠ (434331,8…651497,7) rot/min (se verifică).

- flexionale (de încovoiere), (0…n) ≠ (0,8…1,2)f₀; (0…625) ≠ (0,8…1,2) 160374,53;

(0…625) ≠ (128299,62…192499,44) rot/min (se verifică)