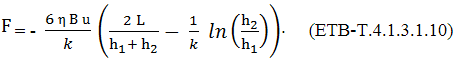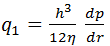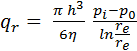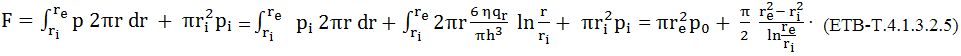ETB. ELEMENTE DE TRIBOLOGIE
ETB-T MODELAREA ŞI CONSTRUCŢIA SISTEMELOR DE UNGERE (LUBRIFICAŢIE)
ETB-T.4.1 DESCIEREA ŞI MODELAREA PROCESELOR DE UNGERE (LUBRIFICAŢIE)
|
CUPRINS |
|
ETB-T.4.1.1 DEFINIŢII ETB-T.4.1.2 CLASIFICARE ETB-T.4.1.3 MODELAREA LUBRIFIERILOR ETB-T.4.1.3.1 Modelarea lubrifierii hidrodinamice ETB-T.4.1.3.2 Modelarea lubrifierii hidrostatice ETB-T.4.1.3.3 Modelarea lubrifierii elastohidrodinamice |
ETB-T.4.1.1 DEFINIŢII
Ungerea este procesul complex de formare şi menţinere a filmului de lubrifiant portant care asigură frecarea fluidă.
Caracteristici funcționale suplimentare ale ungerii: transferul căldurii, funcționarea la turații ridicate, funcționarea la turații reduse, posibilitatea schimbării poziției de funcționare, asigurarea frecării fluide la mișcări intermitente, evitarea contaminării mediului.
ETB-T.4.1.2 CLASIFICARE
|
Criteriul |
Tipul |
Descriere |
|
Principiul generării peliculei (filmului) de lubrifiant portant |
Hidrodinamică/Gazodinamică |
Se realizează prin introducerea lubrifiantului, fără presiune sau cu presiune redusă, într-un interstițiu sub formă de pană, care odată cu creșterea vitezei relative asigură portanță |
|
Hidrostatică/Gazostatică |
Lubrifiantul este introdus forţat de o pompă exterioară la presiunea și debitul impuse pentru menținerea permanentă a filmului de lubrifiant |
|
|
Tipul fluidului |
Lichide (uleiuri) |
Lichidele sunt medii de ungere incompresibile |
|
Gaze |
Gazele sunt medii de ungere compresibile care asigură frecări foarte reduse care implică transferuri de căldură bune și uzări foarte reduse |
|
|
Semisolide |
Unsori consistente |
|
|
Considerarea deformabilității elastice a materialelor suprafețelor în contact |
Cu suprafețele în contact rigide |
În cazul în care zonele de contact sunt puternic durificate |
|
Elastohidrodinamică |
Zonele superficiale în contact sunt moi |
|
|
Grosimea filmului de lubrifiant |
Cu film subțire |
Grosimea filmului de lubrifiant 1...10 µm |
|
Cu film gros |
Grosimea filmului de lubrifiant 10…100 µm |
ETB-T.4.1.3 MODELAREA LUBRIFIERILOR
ETB-T.4.1.3.1 Modelarea lubrifierii hidrodinamice
|
a
b
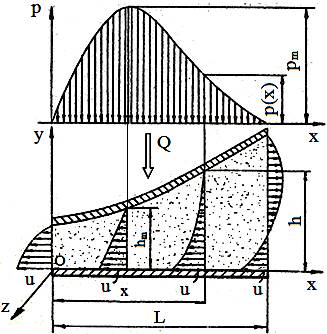
Fig. ETB-T.4.1.3.1.1 Modelul ungerii hidrodinamice bazată pe efectul de pană: a – cazul general (suprafața fixă oarecare); b – cazul particular (suprafața fixă este plană)
Fig. ETB-T.4.1.3.1.2 Modelul ungerii hidrodinamice bazată pe efectul de expulzare (squeeze)
|
Modelul de calcul al ungerii hidrodinamice cu efect de pană Ipotezele modelului de calcul bazat pe efectul de pană (fig. ETB-T.4.1.3.1.1): - procesul hidrodinamic respectă legea de bază a lui Newton, conform rel. (ETB-T.2.4.1.7), - curgerea fluidului este laminară, - fluidul este practic incompresibil, - se neglijează forțele de inerție, - vâscozitatea variază numai cu temperatura, - presiunea este constantă pe grosimea peliculei d elubrifiant, - pubrifiantul aderă la suprafețele pieselor aflate în mișcare relativă, - lungimea pe direcția z este infinită (curgerea se face într-o singură direcți). Ecuația lui Reynolds se constitue ca ecuația hidrodinamică de bază
unidirecțională
care prin integrare conduce la distribuția presiunilor hidrodinamice p în funcție de variațiile grosimii h a peliculei de lubrifiant respectiv a vitezei u și vâscozității η ale lubrifiantului. Pentru cazul particular
(fig. ETB-T.4.1.3.1,b) al interstițiului cu suprafețe plane cu
grosimea [Olaru, 2002],
unde k = tgα , relația (ETB-T.4.1.3.1.1) devine,
Prin
integrarea acestei relații se obține relația,
care prin rearanjare
devine,
Integând această relație se determină expresia presiunii,
Prin impunerea condițiilor limită, pentru x ϵ {0, L}, p= 0, care consideră că atât la intratrea cât și la ieșirea din interstițiu presiunea lubrifiantului este nulă cvasiegală cu presiunea admosferică se obțin constantele de integrare C1 și C2 și forma finală a expresiei presiunii (fig. ETB-T.4.3.1,b),
Din
condiția
Prin înlocuirea relației (ETB-T.4.1.3.1.7) în relația (ETB-T.4.1.3.1.6) se obține grosimea interstițiului (filmului de lubrifiant) în zona maximului de presiune,
Sarcina
pe care o poate susține pelicula de lubrifiant (portanța
hidrodinamică) se determină cu relația
în care B este lățimea suprafețelor plane. Prin înlocuirea relației (ETB-T.4.3.1.6) în relația (ETB-T.4.3.1.9) și calculul integralei se obține, Ungerea hidrodinamică cu efect de expulzare (squeeze) a lubrifiantului se produce în cazul apropierii suprafeţelor active ale cuplei cu viteză mare în direcție normală (fig. ETB-T.4.1.3.1.2); are caracter nestaționar și este determinată de rezistența pe care o opune lubrifiantul la expulzarea sa din interstițiul format de suprafețele cuplei; permanența filmului autoportant se asigură dacă suprafața mobilă are mișcare periodică (ex. amortizoarele hidrodinamice pentru vibrații flexionale ale arborilor)
|
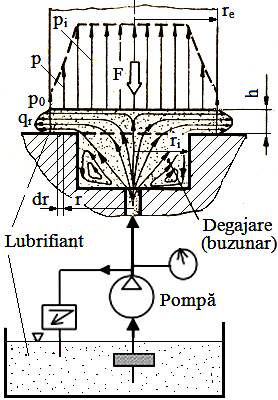
ETB-T.4.1.3.2 Modelarea lubrifierii hidrostatice
|
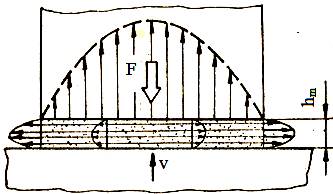
Fig. ETB-T.4.1.3.3 Modelul ungerii hidrostaatice
|
Procesul ungerii hidrostatice Se asigură filmul de lubrifiant prin alimentarea forţat a zonei de frecare la o presiunea necesară astfel încât rezultatnata câmpului de presiuni de pe suprafața activă a cuplei să egaleze sarcina exterioară (fig. ETB-T.4.1.3.3).
Modelul de calcul Debitul de lubrifiant în
direcție radială se obține prin multiplicarea debitului
unitar,
Din această relație se obține variația presiunii în direcție radială,
Astfel, expresia debitului
de lubrifiant devine,
Portanța (forța susținută de filmul de lubrifiant) se calculează ca sumă a forțelor generate de presiunea p din pelicula de lubrifiant existent pe suprafața activă inelară și de presiunea pi exercitată pe suprafața circulară inelară de rază ri:
|
ETB-T.4.1.3.3 Modelarea lubrifierii elastohidrodinamice
|
a b
c Fig. ETB-T.4.1.3.3.1 Modelul ungerii elastohidrodinamice: a – macrogeometria; b – deformarea elastică locală fără ungere; b – deformarea elastică locală cu ungere
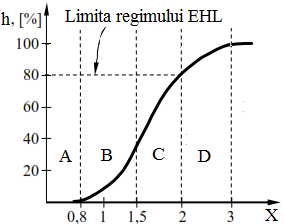
Fig. ETB-T.4.1.3.3.2 Regimuri de frecare la ungerea elstohidrodinamică |
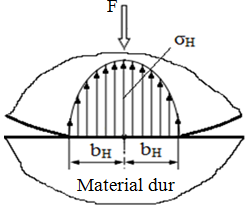
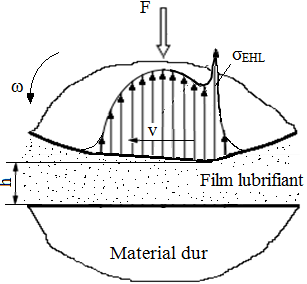
Procesul ungerii elastohidrodinamice Realizarea condițiilor de ungere hidrodinamice presupune transmiterea forțelor prin suprafețe de contact relativ mari (conforme), presiunile care apar pe suprafața de contact fiind reduse și filmul de lubrifiant dintre suprafețe este continuu. În practică există situații multiple (rulmenți, angrenaje, came etc.) în care transmiterea forțelor se face prin cuple de frecare neconforme cu contacte teoretice punctiforme sau liniare puternic încărcate (fig. ETB-T.4.1.3.3.1,a). Conform teoriei lui Hertz, pentru cazul din fig. ETB-T.4.3.3.1,a) distribuția tensiunilor are forma unui elipsoid cu semiaxele a, b, pmax. În afara tensiunilor normale, σHmax = pmax în cazul contactului hertzian nelubrifiat, apare și tensiunea tangențială al cărui maxim τmax = 0,3 σHmax Prezența forțelor de frecare modifică repartiția tensiunilor de contact şi conduce la mărirea tensiunilor de contact. Geometria, cinematica, elasticitatea materialelor contactelor neconforme (punctiforme sau liniare) asigură, în cazul existenței lubrifiantului, condiții de realizare a ungerii hidrodinamice care la sarcini de încărcare mari ca urmare a deformaţiilor elastice superficiale devine ungere (lubrificație) elastohidrodinamică (EHL – ElastoHidrodynamic Lubrification). Analiza regimului elastohidrodinamic, pentru cazul general, este o operație complexă care ia în considerare legile ungerii hidrodinamice combinate cu legile teoriei elasticității și rezolvarea analitică este foarte dificilă, reușindu-se până în prezent doar rezolvări numerice pentru cazuri particulare concrete. Modelelul de calcul al lubrifierii elastohidrodinamice Studiile teoretice și
experimentale au condus la modele obținute experimental care stabilesc
grosimea minimă a peliculei de lubrifiant,
în care, η este vâscozitaea dinamică în Poisie, v – viteza relativă în m/s și Re - raza în mm. Pentru cazurile reale se ia în considerare influența microneregularităților (rugozitățior) asupra regimului de ungere prin intermediul parametrului ,
unde,
În funcţie de valorile acestui parametru se evidenţiază următoarele regimuri de frecare (fig. ETB-T.4.1.3.3.2): - limită sau uscat, Xh < 1 (zona A), este caracteristic cuplelor care transmit sarcini mari, deteriorarea suprafeţelor fiind cauzată de uzarea abrazivă sau de gripaj; - mixt, Xh = 1,1…1,5 (zona B), distrugerea suprafeţelor fiind caracterizată de ciupituri şi exfolieri; - parţial elastohidrodinamic, Xh = 1,5…3 (zona C), pe suprafeţele în contact apar pete lucioase, zone de întrerupere a peliculei de lubrifiant. - complet elastohidrodinamic, Xh = 3 (zona D), pelicula de lubrifiant este egală cu suprafaţa de contact, uzările accidentale sunt reduse
|
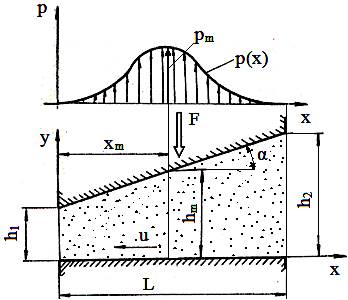

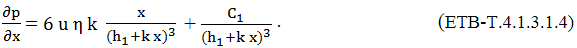
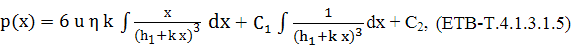
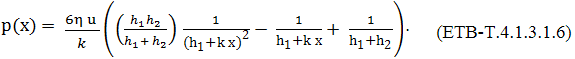
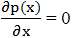 rezultă poziția maximului de presiune,
rezultă poziția maximului de presiune,