ETB ELEMENTE DE TRIBOLOGIE
ETB-T MODELAREA ŞI CONSTRUCŢIA SISTEMELOR DE UNGERE (LUBRIFICAŢIE)
ETB-T.2 DESCRIEREA ŞI MODELAREA PROCESELOR DE FRECARE
|
CUPRINS |
|
ETB-T.2.1 DEFINIŢII ETB-T.2.2 CLASIFICARE ETB-T.2.3 LEGĂTURI MECANICE CU FRECARE ETB-T.2.3.1 Legături mecanice cu mișcare relativă (cuple cinematice) cu frecare (dăunătoare) ETB-T.2.3.2 Legături mecanice fără mișcare relativă (asamblări, transmisii) cu frecare (utilă) ETB-T.2.4 MODELAREA PROCESELOR DE FRECARE DIN CUPLELE CINEMATICE ETB-T.2.4.1 Modelarea frecării uscate ETB-T.2.4.1.1 Modelarea frecării uscate de alunecare ETB-T.2.4.1.2 Modelarea frecării uscate de rostogolire ETB-T.2.4.2 Modelarea frecării fluide ETB-T.2.4.3 Modelarea frecărilor limită și mixtă |
ETB-T.2.1 DEFINIŢII
Frecarea este “un proces complex, de natură moleculară, mecanică şi energetică, care se manifestă între suprafeţele de contact cu mişcare relativă” [Rădulescu, 1981].
Frecarea, conform DIN 50323, este interacţiunea între ariile reale ale corpurilor în contact şi se opune mişcării relative sau tendinței de mișcare.
Frecarea, conform STAS 8069-87, este fenomenul fizic care are loc între două suprafeţe în contact, supuse concomitent la forţa normală de apăsare şi una tangenţială, care se opune stării relative de mişcare.
Obs. Procesele de frecare sunt disipative de energie și conduc la apariția căldurii și modificarea stării de tensiuni și deformații ale celor două elemente în contact contribuind la deformarea și/sau ruperea unui număr de particule metalice de pe suprafeţele în contact (uzarea). Reducerea frecării determină diminuarea consumurilor energetice (creşterea randamentului) şi, în acelaşi timp, mărirea duratei de viață a produselor prin micșorarea uzurilor.
ETB-T.2.2 CLASIFICARE
|
Criteriul |
Tipul |
Descriere |
|
Rolul funcţional |
Dăunătoare |
În procesele/sistemele antifricţiune prin efectele de încălzire, uzare, pierdere de energie (randamente scăzute), încălziri şi dilatări locale, şi vibraţii care conduc la funcţionări necorespunzătoare şi, în final, la scoaterea din uz |
|
Utilă |
În procesele/sistemele de fricţiune (frâne, transmisii prin frecare, cuplaje) prin capacitatea de a transmite a forţelor şi momentelor în condiţiile efectelor negative de încălzire, uzare şi vibraţii |
|
|
Zona în care apare |
Externă |
Apare în zonele suprafețelor în contact ale corpuri sistemelor mecanice |
|
Internă |
În interiorul materialelor (cauciuc); comportare cu histerezis (înmagazinare de energie) |
|
|
Grosimea peliculei de lubrifiant în zona de contact (regimurile de frecare în funcţie de starea de ungere) |
Uscată |
Fără lubrifiant |
|
Limită |
Straturi limită superficiale, rezultate prin oxidare, prin adsorbţia şi/sau chemisorbţia unor molecule |
|
|
Mixtă (semifluidă) |
Peliculă parţială de fluid şi contact direct, parţial, între corpuri. |
|
|
Fluidă |
Separare completă prin pelicula de fluid (ungere hidrodinamică sau elastohidrodinamică). |
|
|
După natura mişcării relative dintre corpuri |
De alunecare |
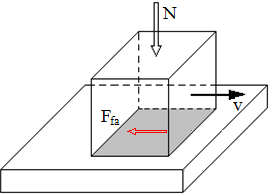
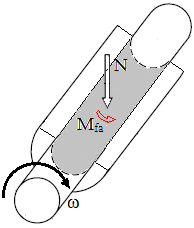
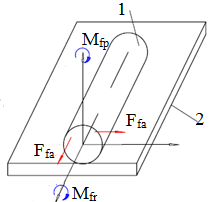
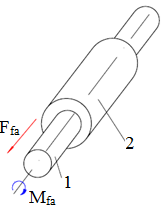
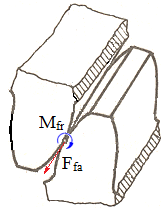
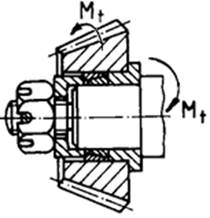
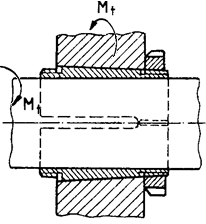
Forța de frecare de alunecare Ffa, la contactul dintre suprafețe plane (fig. ETB-T.2.1,a) sau cilindrice; momentul de frecare de alunecare Mfa, pe suprafețe cilindrice (fig. ETB-T.2.1,b) |
|
De rostogolire |
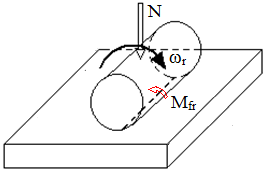
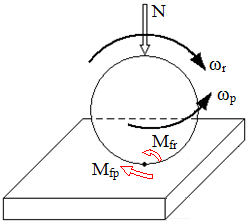
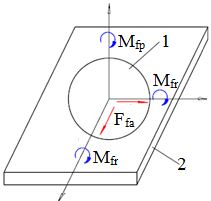
Momentul de frecare de rostogolire Mfr, la rostogolirea unui cilindru pe un plan (fig. ETB-T.2.1,c) sau la rostogolirea unei sfere pe un plan (fig. ETB-T.2.1,e) |
|
|
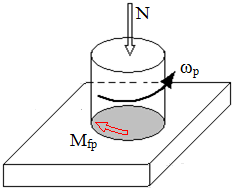
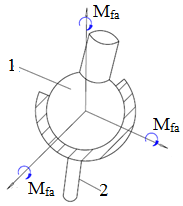
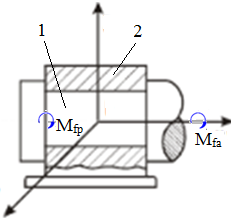
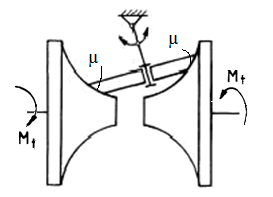
De pivotare (de spin) |
Momentul de frecare de pivotare Mfp, la contactul frontal al unui cilindru cu un plan |
|
|
Combinată |
Rostogolire cu alunecare (roţi dinţate, rulmenţi); rostogolirea cu pivotare (rulmenţi radial-axiali; fig. ETB-T.2.1,d); alunecarea cu pivotare |
|
|
Existenţa mişcării relative |
Statică (de repaus) |
Există tendinţa de mişcare (împiedică apariţia mișcării relative) |
|
Cinetică |
Există mişcare relativă |
|
|
|
|
|
|
|
a |
b |
c |
d |
e |
|
Fig. ETB-T.2.2.1 Tipuri de frecări: a – frecare de alunecare pe suprafață plană; b – frecare de alunecare pe suprafață cilindrică; c – frecare de rostogolire cilindru-plan; d – frecare de pivotare; d – frecare combinată (rostogolire și pivotare) |
||||
ETB-T.2.3 LEGĂTURI MECANICE CU FRECARE
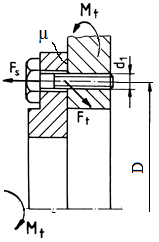
ETB-T.2.3.1 Legături mobile cu mișcare relativă (cuple cinematice) cu frecare (dăunătoare)
Legăturile mobile (cuplele cinematice) cu frecare sunt ansamble cu două sau mai multe corpuri aflate în contact cu mișcări relative (rotații și/sau translații) care au rolul de a transmite sarcini (forțe și/sau momente). Frecarea în aceste legături este dăunătoare și se urmărește, pentru creșterea randamentului, diminuarea ei, cu precădere, prin înlocuirea frecării de alunecare cu cea de rostogolire, prin folosirea de materiale antifricțiune și de sisteme de ungere.
|
Criteriul |
Tipul |
Observaţii |
|
Tipul suprafeţelor de contact |
Conforme (suprafețe conjugate; cuple inferioare) |
Suprafeţele corpurilor în contact se “potrivesc exact” şi se pot deforma împreună; aria de contact este comparabilă cu dimensiunile corpurilor; ex. ghidaje de alunecare, lagăre cu alunecare (fig. ETB-T.2.1, c, d, e, f) |
|
Neconforme (suprafețe neconjugate; contacte hertziene, cuple superioare) |
Suprafeţele în starea neîncărcată pot fi punctiforme sau liniare. La aplicarea încărcării exterioare aria de contact are dimensiuni mult mai mici decât dimensiunile corpurilor; ex. angrenaje, rulmenţi, variatoare (fig. ETB-T.2.1, a, b, h) |
|
|
Numărul mișcărilor relative suprimate |
Clasa I (1 mișcare suprimată) |
Apar 5 rezistențe (forțe și momente) (fig. ETB-T.2.1,a) |
|
Clasa a –II-a (2 mișcări suprimate) |
Apar 4 rezistențe (forțe și momente) (fig. ETB-T.2.1,b) |
|
|
Clasa a –III-a (3 mișcări suprimate) |
Apar 3 rezistențe (forțe și/sau momente) (fig. ETB-T.2.1,c) |
|
|
Clasa a –IV-a (4 mișcări suprimate) |
Apar 2 rezistențe (forțe și/sau momente) (fig. ETB-T.2.1,d) |
|
|
Clasa a –V-a (5 mișcări suprimate) |
Apare 1 rezistență (forță sau moment) (fig. ETB-T.2.1,e) |
|
|
Numărul contactelor |
Cu contact unic |
Fără lubrifiant |
|
Cu contacte multiple |
Straturi limită superficiale, rezultate prin oxidare, prin adsorbţia şi/sau chemisorbţia unor molecule |
|
|
Geometria contactului |
Punctiform |
Cuple de frecare neconforme sau cuple hertziene cu contactul de tip punctual eliptic (rulmenţi şi şuruburi cu bile, rulmenţi cu role butoi, variatoare de turaţie cu elemente intermediare toroidale |
|
Liniar |
Lagăre cu alunecare cilindrice cu joc relativ mare, rulmenţi cu role cilindrice, angrenaje cu roţi dinţate, variatoare cu role cilindrice, lanţuri, cuplaje dinţate etc. |
|
|
Plană |
Lagăre axiale, etanşări frontale, ghidaje, frâne etc. |
|
|
Cilindrică |
Lagăre de alunecare cu joc mic, bucşe pentru lanţuri, curele late, frâne cu tambur etc.), |
|
|
Conică |
Lagărele conice cu joc mic |
|
|
Sferică |
Articulaţii sferice cu joc mic |
|
|
Tipul frecării |
De alunecare |
Fig. ETB-T.2.1, c, e, g) |
|
De rostogolire |
Fig. ETB-T.2.1, a, b, h) |
|
|
De pivotare |
Fig. ETB-T.2.1, a ,b) |
|
|
Combinată |
Fig. ETB-T.2.1, a, h) |
|
|
|
|
|
|
a |
b |
c |
d |
|
|
|
|
|
|
e |
f |
g |
h |
|
Fig. ETB-T.2.3.1 Cuple cu frecare: a – sferă-plan; b – cilindru-plan; c – sferică; d – cilindrică (rototranslație); e – de translație; f – de rotație; g – elicoidală; h – de profilată (angrenaj) |
|||
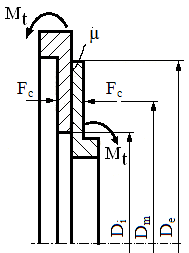
ETB-T.2.3.2 Legături fără mișcare relativă (asamblări, transmisii) prin frecare (utilă)
Legăturile cu frecare de tip ansamble cu două sau mai multe corpuri aflate în contact fără mișcări relative au rolul de a transmite sarcini (forțe și/sau momente), de obicei, active (fluxuri principale de sarcini în asamblări și transmisii). Frecarea în aceste legături este utilă și se urmărește maximizarea ei, cu precădere, prin folosirea contactelor în care apar frecări de alunecare uscate între suprafețe din materiale cu caracteristici de frecare mărite (materiale de fricțiune).
|
|
|
|
|
a |
b |
c |
|
|
|
|
|
d |
e |
f |
|
Fig. ETB-T.2.3.2 Legături prin frecare directe: a – plană; b – prin strângere elastică; c – prin strângere pe con; d – pe suprafețe frontale circulare presate; e – cu flanșe cu șuruburi montate cu joc; f – transmisiii prin elemente flexibile (curele, fire) |
||
|
|
|
|
|
|
a |
b |
c |
d |
|
Fig. ETB-T.2.3.3 Legături prin frecare indirecte (cu elemente intermediare): a – cu element elastic ondulat; b – cu inele tronconice; c – cu bucșă elastică; d – variator de turație toroidal |
|||
ETB-T.2.4 MODELAREA PROCESELOR DE FRECARE DIN CUPLELE CINEMATICE
ETB-T.2.4.1 Modelarea frecării uscate
ETB-T.2.4.1.1 Modelarea frecării uscate de alunecare
|
a b Fig. ETB-T.2.4.1 Procesul frecării uscate de alunecare: a – schema generală; b - detaliu
a b Fig. ETB-T.2.4.2 Modelul clasic al frecării uscate de alunecare: a – schema generală; b - schema forţelor
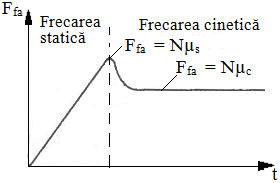
a b Fig. ETB-T.2.4.3: Variațiile parametrilor caracteristici ai frecării: a – coeficientul de frecare; b – forța de antrenare |
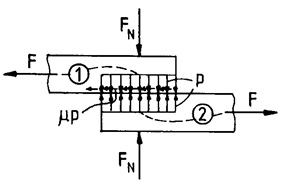
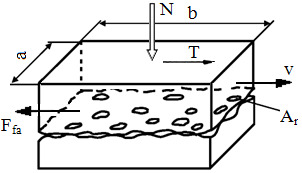
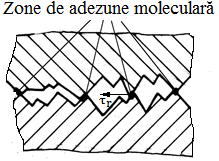
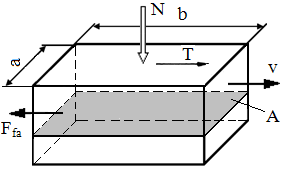
Procesul frecării uscate de alunecare. Odată cu creșterea forței de antrenare, T, în cazul existenței forței de apăsare normală, N, pe suprafețele în contact microneregularitățile se deformează elastic sau plastic și apar forţele de frecare care sunt determinate de rezistenţa la forfecare a microzonelor de adeziune (fig. ETB-T.2.4.1). În cazul mișcării relative punctele de adeziune se rup și în consecință, frecarea uscată se caracterizează prin coeficienţi de frecare mari şi uzuri importante. Legea Amontons-Coulomb,
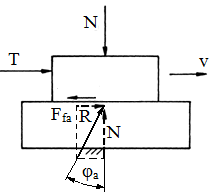
unde, N reprezintă forţa normală de apăsare, Ffa - forţa de frecare de alunecare, μa – coeficientul de frecare de alunecare dependent de tipurile materialelor şi independent de aria de contact A şi de viteza relativă v. Înclinarea reacțiunii (rezultanta dintre forței normală N și forței de frecare Ffa) se poate determina din relația (fig. ETB-T.2.4.2),
tg φa
=
din care φa = arctg µa, unghiul de frecare de alunecare.
Legea Bowden-Tabor
,
unde, N reprezintă forţa normală de apăsare, μa = τr/σc – coeficientul de frecare de alunecare; τr – rezistenţa la forfecare a materialului mai moale (fig. ETB-T.2.4.1,b), σc – tensiunea (rezistența) de curgere la compresiune a materialului mai moale, Ffa - forţa de frecare de alunecare egală cu forţa de rupere a proeminenţelor care formează aria reală de contact, Ar (mult mai mică decât aria nominală A). |
|
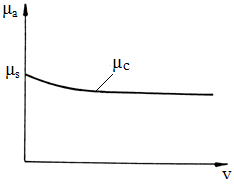
Obs. 1. Coeficientul de frecare de alunecare este variabil cu viteza relativă de deplasare a corpurilor în contact (fig. ETB-T.2.3.3,a): coeficientul de frecare static, µs, când nu există mișcare relativă (v = 0); coeficientul de frecare cinetic, µs, când există mișcare relativă (v > 0). 2. Procesul de frecare în timp (pornire-deplasare) conform variației din fig. ETB-T.2.4.1,b: la forțe de antrenare, T, mici şi crescătoare, forța de frecare crește până când, T= Ffa = µs N și unghiul φ dintre R și N devine φ = φa; după îndeplinirea acestei condiții începe mișcarea relativă și forța de antrenare T scade consecință a scăderii valorii coeficientului de frecare (µc < µs) |
ETB-T.2.4.1.2 Modelarea frecării uscate de rostogolire
|
a
b
Fig. ETB-T.2.4.4 Modele ale frecării uscate de rostogolire: a – roată în plan orizontal; b – roată în pantă |
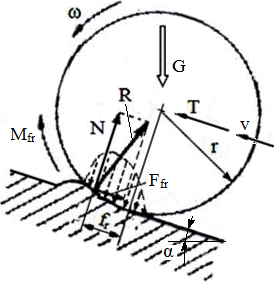
Procesul frecării uscate de rostogolire. În cazul, real corpurile în contact sunt deformabile elastic şi rezistenţa la deplasare sub acțiunea forței de antrenare T este determinată de forţa rezultantă, N, a presiunilor pe suprafaţa de contact care se concentreză într-un punct plasat în afara planului de simetrie la distanţa, fr (fig. ETB-T.2.4.4). Din ecuațiile de echilibru (fig. ETB-T.2.4.5),
T = Ffr; N fr = T r, (ETB-T.2.4.1.4)
rezultă,
Mfr = fr N, (ETB-T.2.4.1.6)
unde: Ffr reprezintă forța de frecare de rostogolire (de rezistenţă la rulare), μr = fr/r - coeficientul (factorul) rezistenţei (de frecare) la rostogolire (rulare), Mfr - momentul de frecare de rostogolire, r – raza roţii.
Stări de mișcare posibile: - Repaus: T < N fr/r, T r < Mfr;
- Mişcarea de alunecare: T > N fr/r, T r < Mfr;
- Mişcarea de rostogolire: T < N fr/r, T r > Mfr se va amorsa rostogolirea cu atât mai uşor cu cât coeficentul de frecare la rostogolire (fr/r) este mai mic;
- Mişcare combinată de rostogolire şi alunecare (cazul real): T > N fr/r, T r > Mfr.
Obs. În cazul roţilor vehiculelor , N = G (rulare pe orizontală, fig. ETB-T.2.4.4,a), sau N = G cosα, (rulare în pantă fig. ETB-T.2.4.4,b), rezistenţa la rulare devine, Ffr = µr G sau, respectiv, Ffr = µr G cosα, unde: G reprezintă greutatea pe roată, α - unghiul căii de rulare; coeficientul de rezistenţă la rulare µr , frecvent notat cu f, are valoarea medie f = 0,018, pentru cale de rulare din asfalt sau beton) |
ETB-T.2.4.2 Modelarea frecării fluide
|
a
b
Fig. ETB-T.2.4.6 Frecarea fluidă: a – schema cu parametri; b – modelul simplificat |
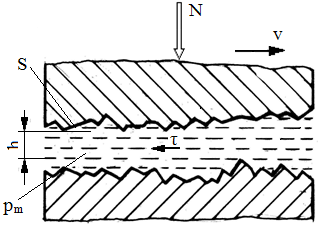
Frecarea fluidă apare în cazul în care suprafeţele în contact sunt separate de o peliculă (film) de lubrifiant h mai groasă decât înălţimile maxime a asperităţilor (fig. ETB-T.2.4.6,a). Forțele care se opun deplasării relative sunt generate de tensiunile tangenţiale din fluid, care conform legii lui Newton, se determină cu relația,
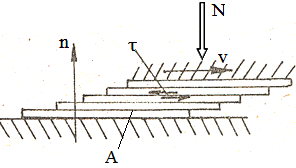
în care, η [N s/m2] reprezintă vâscozitatea dinamică a lubrifiantului; v [m/s] – viteza relativă; n [m] – distanţa în direcția normală; la limită considerând: dv = Δv = v, dn = Δh = h, rezultă forma simplificată a legii lui Newton, τ = η v/h. Procesul de frecare din interiorul fluidului se studiază conform teoriei mecanicii fluidelor. Model de calcul simplificat Convențional, se poate considera că forța de frecare este rezultatul forfecării interne a fluidului la nivelul suprafeței de contact de arie A (fig. ETB-T.2.4.6,b),
Din această relație
ținând cont de relația (ETB-T.2.4.1.7) la limită, se obține,
coeficientul de frecare din fluid,
unde pm este presiunea medie din lubrifiant, h – grosimea peliculei de lubrifiant; practic, µf = 10-4 ...10-2. Forța normală exterioară este preluată de rezultanta forțelor de presiune existente în pelicula de lubrifiant poartă denumirea de forță portantă sau portanță. Frecarea fluidă se realizează în două situații de ungere distincte: ungerea hidrodinamică și hidrostatică |
ETB-T.2.4.3 Modelarea frecărilor limită și mixtă
|
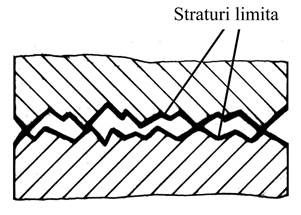
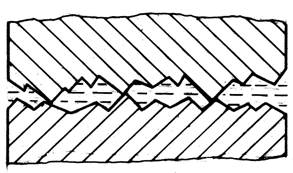
a b Fig. ETB-T.2.4.7 Schemele frecărilor intermediare: a – limită; b – mixtă
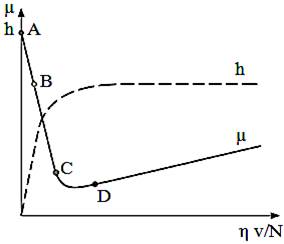
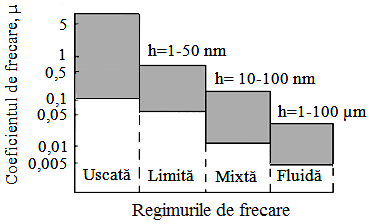
a b Fig. ETB-T.2.4.8 Variația coeficientului de frecare: a - curba Stribeck; b - valori informative [Wen, 2012] |
Frecarea limită (semiuscată) se realizează atunci când între suprafeţele în contact apar straturi subţiri (limită) de ordin molecular (fig. ETB-T.2.4.7,a), formate, ca urmare, a unor fenomene de natură fizică (adsorbția) şi/sau chimică (chemisorbția). Datorită legăturilor intermoleculare (de tip Van der Waals) din cadrul acestui strat mult mai reduse decât în cazul legaturilor de adeziune moleculară (frecarea uscată), forţele de frecare scad de 2…3 ori iar uzarea se poate micşora de sute sau chiar de mii de ori. Şi în cazul frecării limită se aplică legile frecării clasice. Frecarea mixtă (semifluidă) apare în situaţiile în care se formează un film de lubrifiant întrerupt de rugozitățile suprafețelor în contact (fig. ETB-T.2.4.7,b). Convenţional, forţele de frecare se calculează ca la frecarea uscată luând în considerare coeficienți de frecare (v. fer. ETB.P.1.1) care sunt dependenți și de rugozitatea suprafețelor. În regimul de frecare mixtă, apare frecvent fenomenul de stick-slip (prindere-alunecare), caracterizat printr-o alternanţă periodică, rapidă, între frecarea de aderenţă (statică) şi cea de alunecare, mişcarea fiind sacadată.
În fig. ETB-T.2.4.8,a se prezintă variația coeficientului de frecare, µ, și grosimii peliculei de lubrifiant, h, în funcție de produsul dintre vâscozitatea dinamică (η) și viteza relativă (v) raportat la forța de apăsare (N). Astfel, se identifică următoarele zone: AB – frecare uscată sau limită; BC – frecare mixtă; CD – frecare fluidă
|
 ,
(ETB-T.2.4.3)
,
(ETB-T.2.4.3)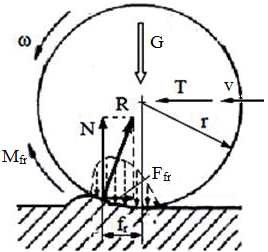
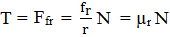 ,
,
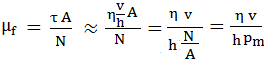 , (ETB-T.2.4.1.9)
, (ETB-T.2.4.1.9)