ARD.
ARBORI ŞI OSII
ARD-T.
CONSTRUCŢIA ŞI MODELAREA ARBORILOR ŞI OSIILOR
|
CUPRINS
|
|
ARD-T.1 DEFINIRE
ARD-T.2
STRUCTURA CONSTRUCTIVĂ
ARD-T.3 DOMENII DE UTILIZARE
ARD-T.4 CLASIFICARE
ARD-T.5 MATERIALE ŞI
TEHNOLOGII
ARD-T.6 FORME ŞI CAUZE DE
SCOATERE DIN UZ SAU DE COMPORTARE NECORESPUNZĂTORE
ARD-T.7 PARMETRII
FUNCŢIONALI ŞI CONSTRUCTIVI
ARD-T.8 MODELE DE CALCUL A ARBORILOR DREPŢI
ARD-T.8.1 Modele
de calcul a forţelor şi eforturilor
ARD-T.8.1.1 Model de calcul a forţelor şi eforturilor unui
arbore intermediar al unui reductor cilindric de turaţie
ARD-T.8.2
Modele de calcul a tensiunilor
ARD-T.8.2.1 Model de calcul a tensiunilor din arborele intermediar al
unui reductor cilindric de
turaţie
ARD-T.8.3 Modele
de calcul a deformaţiilor
ARD-T.8.3.1
Model de calcul a deformaţiilor de încovoiere
(flexionale)
ARD-T.8.3.2
Model de calcul a deformaţiilor de torsiune
(torsionale)
ARD-T.8.4 Modele
de calcul la solicitări variabile (oboseală)
ARD-T.8.5 Modele
de calcul la vibraţii
ARD-T.8.5.1
Model de calcul a la vibraţii transversale
(flexionale)
ARD-T.8.5.2
Model de calcul a la vibraţii torsionale
ARD-T.9 MODELE DE CALCUL A OSIILOR
|
ARD-T.1
DEFINIRE
Arborii drepţi sunt elemente de
maşini cu mişcare de rotaţie destinate susţinerii altor
elemente de maşini (roţi
dinţate, roţi de curea, semicuplaje, volanţi etc.) şi transmiterii momentelor
de torsiune, care, la rândul lor, se sprijină prin intermediul
lagărelor (cu alunecare sau cu rostogolire) pe structuri, de obicei, fixe
(şasiuri, batiuri, carcase etc.).
Osiile sunt organe de
maşini în mişcare de rotaţie sau fixe, destinate susţinerii altor organe de
maşini cu mişcare de rotaţie (nu transmit momente de torsiune).
ARD-T.2
STRUCTURĂ CONSTRUCTIVĂ
|
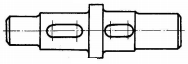 |
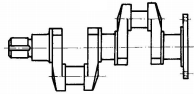 |
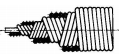 |

|
 |
 |
 |
|
a |
b |
c |
d |
e |
f |
g |
|
Fig.
ARD-T.3.1
Tipuri de arbori şi osii:
a –
arbori drepţi; b
- arbori
cotiţi; c,
d, e,
-
arbori flexibili;
f -
osie rotitoare (pentru vagon de cale ferată);
g
-
osie fixă (pentru scripete) |
|
Obs.
a. Arborii
cotiţi au două sau mai multe fusuri paliere, dispuse pe lungimea
arborelui, pentru a asigura o rigiditate mare construcţiei şi unul sau
mai multe fusuri manetoane, de legătură cu biela (bielele mecanismului
motorului);
arborii cotiţi pot fi prevăzuţi cu contragreutăţi, pentru echilibrarea
statică şi dinamică.
b. Arborii flexibili
au axa geometrică cu forme variabilă în timp; sunt confecţionaţi din
straturi de sârmă, înfăşurate strâns şi în sensuri diferite, sensul de
înfăşurare al ultimului strat fiind invers sensului de rotaţie al
arborelui, pentru a realiza, în timpul transmiterii mişcării, strângerea
straturilor interioare de către stratul exterior (ARD-T.3.1,
c); pentru protecţia arborelui
împotriva deteriorării şi a murdăriei şi pentru menţinerea unsorii
consistente între spire, arborele flexibil se introduce într-o manta
metalică (ARD-T.3.1, d)
sau executată din ţesătură cauciucată (ARD-T.3.1,
e); arborele flexibil se racordează
la elementele între care se transmite mişcarea cu ajutorul armăturilor
de capăt. |
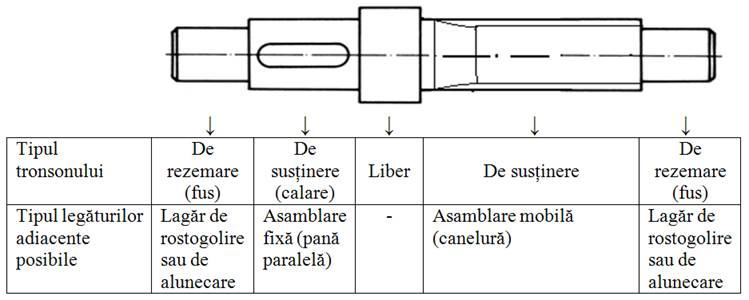
Fig.
ARD-T.2.1 Structura constructivă generală a arborilor
drepţi
ARD-T.3 DOMENII DE UTILIZARE
Arborii sunt utilizaţi în transmisiile automobilelor, tractoarelor,
maşinilor agricole, utilajelor tehnologice, maşinilor unelte, toate
transmisiile cu angrenaje, reductoarele de turaţii etc.
Arborii cotiţi se folosesc în construcţia mecanismelor de tip
bielă-manivelă, pentru transformarea mişcării de translaţie în mişcare de
rotaţie (la motoarele cu ardere internă) sau invers (la compresoare, prese,
maşini de forjat).
Arborii flexibili se folosesc pentru transmiterea momentelor de torsiune
între subansamble care îşi schimbă poziţia relativă în timpul funcţionării.
ARD-T.4 CLASIFICARE
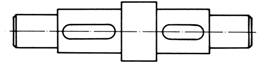
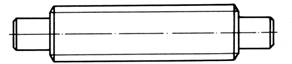
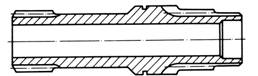
Tab. ARD-T.4.1 Clasificarea arborilor drepţi [Moldovean, 1998]
|
Criteriul
|
Tipul arborelui
|
|

|
|
|
a
|
b
|
|
|
|
|
c
|
d
|
|
Fig. ARD-T.4.1 Forme principale ale arborilor drepţi: a - cu secţiune plină; b - în trepte; c -
canelat; d - tubular
|
|
|
Variaţia secţiunii arborelui pe
lungime
|
Cu secţiune constantă (lişi) (fig.
ARD-T.4.1, a)
|
Cu secţiune variabilă, în trepte (fig.
ARD-T.4.1,b)
|
|
Forma secţiunii
transversale
|
Cu secţiune plină (fig. ARD-T.4.1,
a,b,c)
|
Tubular (fig. ARD-T.4.1,d)
|
|
Rigiditatea (regimul de funcţionare)
|
Rigid
|
Elastic
|
|
Numărul reazemelor
|
Cu două reazeme
(static determinat)
|
Cu trei sau mai multe reazeme (static nedeterminat)
|
|
Poziţia axei geometrice
|
Orizontali
|
Înclinaţi
|
Verticali
|
|
|
|
|
|
|
ARD-T.5
MATERIALE ŞI TRATAMENTE TERMICE
Pentru
execuţia arborilor drepţi se utilizează frecvent, oţelurile:
- de
uz general pentru construcţii (E295, E335, E360)
care nu necesită tratament termic, pentru cazuri cu sarcini reduse;
- carbon
de calitate de îmbunătăţire (C 45, C55 etc.) şi oţeluri aliate de
îmbunătăţire (40 Cr 10, 41 CrNi 12 etc.), pentru sarcini şi
durate medii de funcţionare;
-
carbon de calitate de cementare (C 15, C 20
etc.) şi aliate de cementare (13 CrNi 30 ), pentru sarcini puternice şi turaţii înalte.
Fontele
sunt utilizate pentru execuţia arborilor de dimensiuni mari deoarece sunt
mai puţin sensibile la efectul concentratorilor de tensiuni şi
amortizează mai bine vibraţiile.
Tratamentele termice sau termochimice aplicate depind de materialul
din care se execută arborii, putând fi: îmbunătăţire
sau îmbunătăţire şi călire superficială a
fusurilor, canelurilor, porţiunilor de calare etc.; cementare
urmată de călire a fusurilor, porţiunilor de calare şi
a canelurilor; nitrurare etc.
ARD-T.6 FORME ŞI CAUZE DE
SCOATERE DIN UZ SAU DE COMPORTARE NECORESPUNZĂTOARE
Tab. ARD-T.6.1 Forme şi cauze de scoatere din uz sau de comportare
necorespunzătoare [Moldovean, 1998]
|
Tipul
cedării
|
Forme
|
Apariţie
|
Cauze
|
Manifestare
|
Evitare
|
|
Scoatere din uz
|
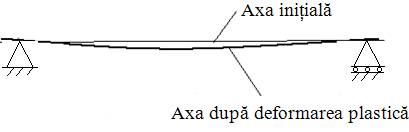
Deformarea plastică
|
Arbori din materiale moi puternic solicitaţi
|
Depăşirea limitei de curgere a
materialului
|
Modificarea permanentă a formei axei geometrice urmată de deteriorarea elementelor
adiacente (rulmenţi, roţi dinţate; fig. ARD-T.6.1, a)
|
Calcul de verificare la deformaţii
flexionale; protecţie la suprasarcini
|
|
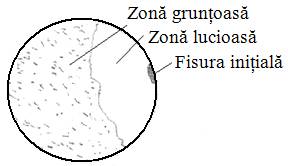
Ruperea la suprasarcini
|
Arbori din materiale dure puternic solicitaţi
|
Depăşirea limitei de rupere a materialului
|
Ruperea arborelui (fig.
ARD-T.6.1, b)
|
Calcul de
rezistenţă, protecţie
la suprasarcini
|
|
Ruperea la oboseală
|
Arbori încărcaţi cu sarcini variabile
periodic
|
Depăşirea rezistenţei la
oboseală
|
Ruperea arborelui (fig.
ARD-T.6.1, c)
|
Calculul la
oboseală; soluţii constructive de creşterea rezistenţei la oboseală
|
|
Comportare necorespunzătoare
|
Deformaţii elastice flexionale şi/sau torsionale
|
Arbori puternic solicitaţi
|
Elasticitate mărită şi sarcini
puternice
|
Săgeţi mărite la încovoiere şi torsiune care
conduc la funcţionarea necorespunzătoare a angrenajelor şi
lagărelor
|
Calculul de
verificare la
deformaţii flexionale/ torsionale; soluţii constructive
de rigidizare
|
|
Vibraţii
|
Arbori cu turaţii mari
|
Abateri tehnologice şi de montaj cu
solicitări variabile
|
Vibraţii cu amplitudini mărite
(rezonanţă) care conduc la funcţionarea necorespunzătoare
a angrenajelor şi lagărelor
|
Calculul la
vibraţii (turaţia critică);
soluţii constructive de rigidizare
|
|
Deformaţii termice
|
Arbori lungi ce lucrează în medii cu temperaturi ridicate
|
Creşterea temperaturii
|
Alungirea tronsoanelor arborelui, fapt ce
conduce la funcţionarea necorespunzătoare, mai ales, a rulmenţilor
|
Calculul termic,
soluţii de compensare
(neîmpiedicare)
a deformaţiilor termice
|
|
|
|
|
|
a
|
b
|
c
|
|
Fig. ARD-T.6.1
Forme de scoatere din uz a arborilor: a
– deformare plastică; b-
rupere la suprasarcini; c - rupere
la oboseală
|
|
|
|
|
|
|
|
|
ARD-T.7 PARAMETRI
FUNCŢIONALI ŞI CONSTRUCTIVI
Tab. ARD-T.7.1 Parametrii funcţionali şi constructivi
principali
|
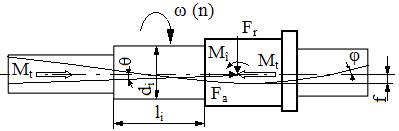
Fig. ARD-T.7.1 Schema parametrilor principali
|
Mt [Nmm] – momentul de torsiune transmis;
ω [rad/s] (n [rot/min]) – viteza
unghiulară (turaţia), ω = π n/30, n=30 ω/π;
Mî [Nmm] – momentul de încovoiere;
Fr [N] – forţa radială;
Fa [N] – forţa axială;
f [mm] –
săgeata la încovoiere;
φ [grade] – rotirea la încovoiere;
θ [grade] – rotirea la torsiune (răsucire);
di ,
li [mm] – diametrul, lungimea tronsonului i
|
ARD-T.8
MODELE DE CALCUL A ARBORILOR DREPŢI
ARD-T.8.1
Modele de calcul a forţelor şi eforturilor secţionale
Arborii drepţi au structuri spaţiale 3D care sunt
încărcate extern cu sarcini distribuite şi variabile în timp.
Ipoteze simplificatoare:
-
arborii
se consideră cu structuri
unidimensionale;
-
forţele
distribuite din zonele de interacţiune ale arborelui cu elementele
adiacente (susţinute şi de susţinere) se consideră
echivalente cu un sistem de forţe concentrate conform unor scheme de
echivalare dependente de: tipul montajului, rigiditatea
pieselor montate etc.
(fer.
ARD-P.1- angrenaje;
fer.
ARD-P.2
– curele, lanţuri);
-
schematizarea
reazemelor arborilor prin înlocuirea cu reazeme convenţionale (cu unul sau
mai multe grade de libertate) ţine cont de tipul lagărului (cu
alunecare, cu rostogolire), rigiditatea arborelui în zona de susţinere (fer.
ARD-P.3 - rulmenţi,
fer.
ARD-P.4 - lagăre cu alunecare).
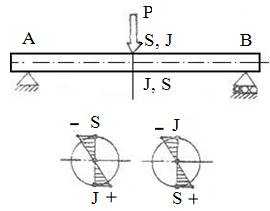
ARD-T.8.1.1 Model de calcul a forţelor
şi eforturilor secţionale ale unui arbore intermediar al unui
reductor cilindric de turaţie
Tab. ARD-T.8.1.1 Parametrii de calcul şi diagrame de eforturi
[Manea, 1970]
|
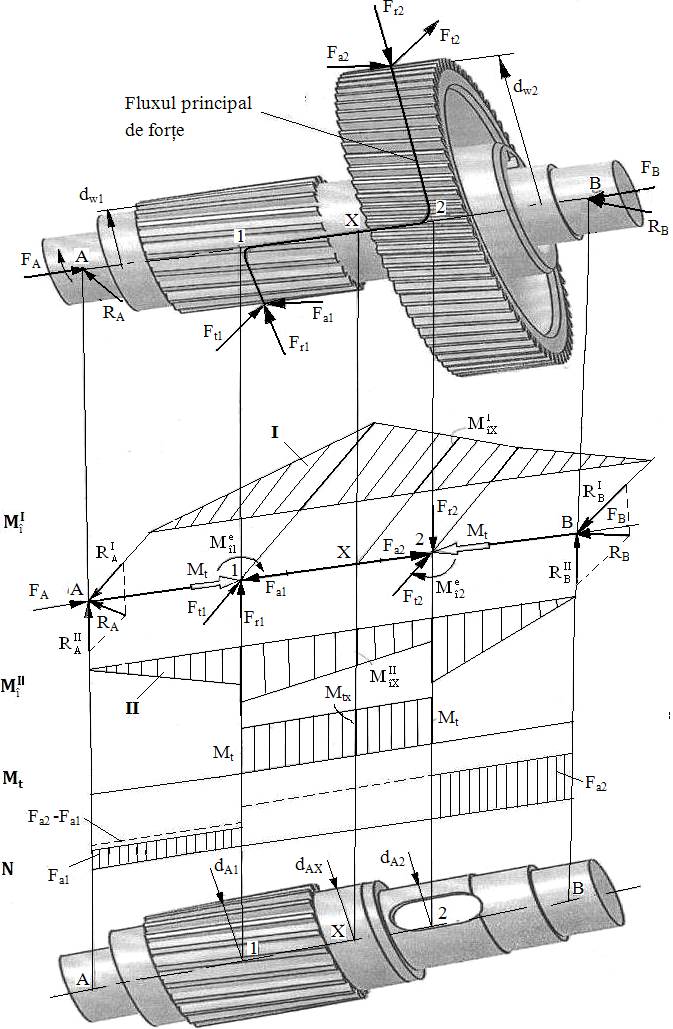
Fig. ARD-T.8.1 Model de calcul a forţelor şi
eforturilor secţionale ale arborelui intermediar
|
Modelare
geometrică
Arborele se consideră, având la
bază ipotezele simplificatoare de mai sus, o bara dreaptă, AB, cu
secţiunea în trepte (fig. ARD-T.8.1)
Încărcare externă
Pinionul 1 (conducător): forţa normală din
angrenajul treptei a II-a (v. subcap. AEV-T.7.2.2, forţe în angrenajul
cu dantură înclinată) cu componentele: forţa tangenţială, Ft1; forţa radială, Fr1;
forţa axială, Fa1.
Roata 2 (condusă): forţa normală din
angrenajul treptei I cu componentele: forţa
tangenţială, Ft2; forţa radială, Fr2; forţa axială, Fa2.
Reazemele A şi B
Bara asociată arborelui este
rezemată în zona de montaj a rulmenţilor radiali în punctele A
şi B în care se consideră, conform schemelor de rezemare simplificată
din fer. ARD-P.4, reacţiunile RA şi, respectiv, RB
– în plan transversal – şi FA
şi, respectiv, FB – în
direcţie axială.
Schema
de încărcare a arborelui cu forţe concentrate (la nivelul axei)
Secţiunea 1: forţa tangenţială, Ft1;
forţa radială, Fr1; forţa axială, Fa1;
momentele de torsiune şi de
încovoiere:
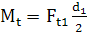 , , 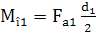 .
(ARD-T.8.1) .
(ARD-T.8.1)
Secţiunea 2: forţa tangenţială, Ft2;
forţa radială, Fr2; forţa axială, Fa2
momentele de torsiune şi de încovoiere:
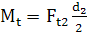 , , 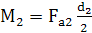 .
(ARD-T.8.2) .
(ARD-T.8.2)
Diagramele
de variaţie a eforturilor secţionale
Momentul de
torsiune, Mt ,
este constant pe porţiunea 1-2.
Momentul de încovoiere, Mî, este variabil spaţial
de-a lungul barei şi, pentru calculul clasic, în corelaţie cu
sistemul de coordonate triortogonal drept asociat forțelor, se reprezintă prin proiecţiile în
planele perpendiculare, I şi II. Relaţia de calcul a momentului de
încovoiere în secţiunea X este
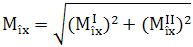 ,
(ARD-T.8.3) ,
(ARD-T.8.3)
în care, 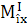 este
momentul de încovoiere în planul I şi, este
momentul de încovoiere în planul I şi, 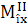 -
momentul de încovoiere în planul II. -
momentul de încovoiere în planul II.
Eforturile secţionale
axiale, N,
consecinţă a acţiunilor forţelor axiale din angrenaje au
variaţie constantă de-a lungul tronsoanelor arborelui cu valori
dependente şi de sensul de rotaţie (tab. ARD-T.8.1.2)
Tab. ARD-T.8.1.2 Eforturi secţionale axiale
|
|
Tronsonul
|
A-1
|
1-2
|
2-B
|
Reacţiunile
axiale, FA,B
|
|
Sensul
de rotaţie
|
Efortul
secţional axial, N
|
|
Antiorar
|
Fa1
|
-
|
Fa2
|
FA= Fa1; FB= Fa2
|
|
Orar
|
Fa2 - Fa1
|
Fa2
|
-
|
FA= Fa2 - Fa1; FB= 0
|
|
Forţele
tăietoare, au valori
reduse şi se neglijează
|
ARD-T.8.2
Modele de calcul a tensiunilor
ARD-T.8.2.1 Model de calcul a tensiunilor din
arborele intermediar al unui reductor cilindric de turaţie
Sub acţiunea forţelor
prezentate mai sus în structura arborelui apar solicitări (tensiuni) de
torsiune, încovoiere, compresiune şi forfecare (neglijabile), distribuite
neuniform şi, datorită dependenţei valorilor
încărcărilor de timp, variabile în timp [Moldovean, 1998; Catrina,
2002].
Tab. ARD-T.8.1.3 Relaţiile de calcul a tensiunilor din
secţiunea transversală X (fig.
ARD-T.8.1)
|
Tipul
tensiunii
|
Tensiuni
simple
|
Tensiunea
echivalentă (conform teoriei tensiunilor tangenţiale maxime)
|
|
Torsiune
|
Încovoiere
|
Compresiune/tracţiune
|
|
Relaţiile de calcul
|
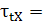 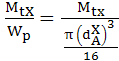
|
(ARD-T.8.4)
|
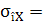 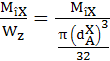
|
(ARD-T.8.5)
|
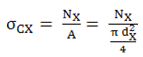
|
(ARD-T.8.6)
|
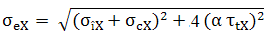
|
(ARD-T.8.7)
|
|
Obs.
a.
Semnificaţiile parametrilor din
relaţiile de calcul: Mtx, Mîx şi Nx
sunt momentul de torsiune, momentul de încovoiere şi, respectiv,
forţa axială în secţiunea X (v. rel. ARD-T.8.1, ARD-T.8.2,
ARD-T.3 şi tab. ARD-T.8.1.2); Wp, Wz şi A –
modulul de rezistenţă polar, modulul de rezistenţă axial,
şi, respectiv, aria secţiunii transversale în punctul X; 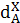 –
diametrul secţiunii circulare X; –
diametrul secţiunii circulare X; 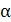 -
factorul ciclurilor de solicitare. -
factorul ciclurilor de solicitare.
b.
Tensiunile de încovoiere şi de torsiune
nu sunt constante în timp. Deoarece,
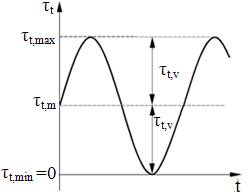
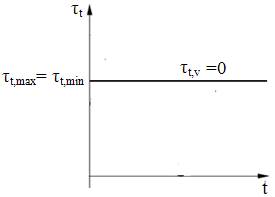
arborele este un element rotitor (fig. ARD-T.8.2) tensiunea de încovoiere
este variabilă după un ciclu alternant simetric (fig.
ARD-T.8.3,a). Pentru cazul rotirii arborelui într-un sens, variaţia
tensiunii de torsiune, în funcţie de tipurile antrenării
şi sarcinii de învins, se poate echivala cu un ciclu pulsator
(fig. ARD-T.8.3,b) sau constant (fig. ARD-T.8.3,c).
c.
Ciclurile
solicitărilor variabile se evidenţiază cu ajutorul factorului
de asimetrie R (fer.
ARD-F.1) dar, pentru calcule de proiectare, se
marchează şi cu simbolurile: I , pentru ciclul constant
(R=1); II, pentru ciclul pulsator (R=0); III, pentru ciclul
alternant simetric (R=0).
d. Factorul 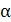 , din relaţia
(ARD-T.8.7), echivalează tensiunile componente din punct de vedere al
ciclurilor de variaţie (tensiunile variabile conform ciclurilor I
şi II cu tensiuni variabile după ciclul III), se determină cu
relaţiile: , din relaţia
(ARD-T.8.7), echivalează tensiunile componente din punct de vedere al
ciclurilor de variaţie (tensiunile variabile conform ciclurilor I
şi II cu tensiuni variabile după ciclul III), se determină cu
relaţiile:
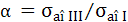 , pentru cazul momentului
de torsiune constant; , pentru cazul momentului
de torsiune constant;
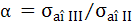 , pentru cazul momentului de torsiune pulsator. , pentru cazul momentului de torsiune pulsator.
Valorile
orientative ale tensiunilor σaîI, σaîII,
σaîIII corespunzătoare celor trei cicluri de
variaţie caracteristice, asociate materialelor uzuale pentru arbori,
sunt prezentate în
fer.
ARD-M.1
e.
În cazurile practice, pentru
calculele de proiectare, se neglijează efectul eforturilor axiale (acesta
fiind mult redus în raport cu al celorlalte eforturi) şi în relaţia (ARD-T.8.7)
se consideră σcX
= 0.
|
|
Relaţia tensiunii
echivalente (ARD-T.8.7), neglijând tensiunea de compresiune (σcx=0)
şi considerând Wp=2Wz, devine,
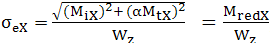 , (ARD-T.8.8) , (ARD-T.8.8)
unde MredX este numit momentul
echivalent în secţiunea X.
Tab. ARD-T.8.1.4 Parametrii şi relaţiile de calcul
|
|
Tipul calculului
|
Verificare
|
Dimensionare
|
Sarcina
capabilă
|
|
Relaţii de calcul
|
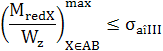
|
(ARD-T.8.9)
|
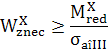
|
(ARD-T.8.10)
|
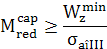
|
(ARD-T.8.11)
|
|
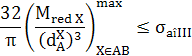
|
(ARD-T.8.12)
|
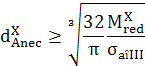
|
(ARD-T.8.13)
|
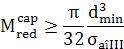
|
(ARD-T.8.14)
|
|
Obs.
Deoarece relaţia tensiunilor compuse (ARD-T.8.8) este dependentă
neliniar de Mî, Mt şi dx şi, deci,
verificarea arborelui la solicitări compuse se face în mai multe
secţiuni transversale
|
|
|
|
|
|
|
a
|
b
|
c
|
|
Fig. ARD-T.8.2 Schematizarea
variaţiei tensiunii de încovoiere în plan transversal
|
Fig. ARD-T.8.3 Ciclurile de
variaţie a tensiunilor: a –
alternant simetric (frecvent pentru încovoiere); b - pulsator (torsiune);
c
– constant (torsiune)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ARD-T.8.3
Modele de calcul la
deformaţii (rigiditate)
Sub acţiunea sarcinilor exterioare arborii
sunt supuşi deformaţiilor de încovoiere (flexionale) şi de torsiune
(torsionale).
ARD-T.8.3.1
Model de calcul a deformaţiilor de încovoiere
(flexionale)
|
a
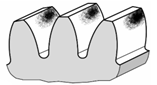
b
c
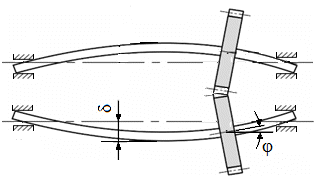
Fig. ARD-T.8.4 Angrenajul
real cu deformaţii elastice: a –
schema deformaţiilor (săgeţi δ şi rotiri
φ); b - pata de contact în cazul arborilor rigizi (ideal);
c
– pata de contact în cazul arborilor elastici |
Scop,
particularităţi de calcul şi limite |
|
Calculul deformaţiilor flexionale, în
general, se efectuează în scopul preîntâmpinării funcţionărilor
necorespunzătoare (cu vibraţii transversale şi zgomote) ale
elementelor susţinute (în special, roţi dinţate) şi a lagărelor (fig.
ARD-T.8.4).
Calculul la deformaţii de încovoiere
(de verificare) constă în determinarea valorilor săgeţilor sub
organele susţinute (roţi dinţate) şi a deformaţiilor unghiulare (rotirilor)
din lagăre şi limitarea acestora la valori admisibile (δ
≤ δa,
φ
≤
φa
).
Valorile admisibile ale deformaţiilor de încovoiere, recomandate
în literatura de specialitate, sunt: pentru săgeţile de sub roţile
dinţate montate pe arbore δa
≤ (0,01 ... 0,03)m, m fiind modulul angrenajului, în mm; pentru
deformaţiile unghiulare, în radiani:
φa
≤ 8.10-3
– pentru lagăre cu rulmenţi radiali cu bile;
φa
≤ 2,5.10-3 – pentru lagăre cu rulmenţi radiali cu role
cilindrice;
φa
≤ 1,7.10-3
– pentru lagăre cu rulmenţi radial-axiali cu bile
sau cu role conice;
φa
≤ 5.10-2
– pentru lagăre cu rulmenţi radial oscilanţi cu bile
sau cu role butoi pe două rînduri;
φa
≤ 10-3 – pentru lagăre cu alunecare.
Metodele de calcul a deformaţiilor
flexionale pot fi analitice, cu precădere, studiate la Rezistenţa
materialelor sau numerice implementate în pachetele performante actuale.
Pentru cazurile simple, în literatura de specialitate, se dau ecuaţiile
fibrei medii deformate şi expresiile săgeţilor maxime. Actual calculul
deformaţiilor se realizează cu pachete software performante (de ex.
MDESIGN) care iau în considerare arborii cu formele şi dimensiuniile
reale. Calculul clasic (manual) al deformaţiilor de încovoiere se face
pe baza schemelor folosite la calculul la solicitări compuse (tab.
ARD-T.8.1.3), deformaţia rezultantă
obţinându-se prin însumarea vectorială a deformaţiilor din cele două
plane perpendiculare de solicitare a arborelui de către forţele
exterioare.
Dacă deformaţiile
efective nu sunt mai mici decât cele recomandate în literatura de
specialitate (nu sunt îndeplinite condiţiile de verificare),
se măreşte rigiditatea arborelui la încovoiere, prin mărirea
diametrului acestuia. |
ARD-T.8.3.2
Model de calcul a deformaţiilor de
torsionale (răsucire)
|
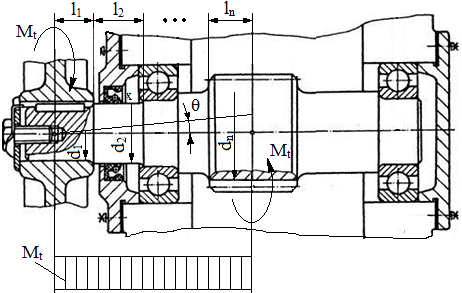
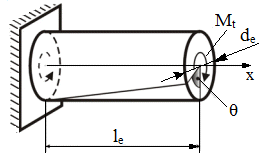
a
b
Fig. ARD-T.8.5 Scheme
de calcul a deformaţiilor torsionale:
a – arborelui în trepte; b - arborele cu secţiune constantă (echivalent)
|
Scop, model de
calcul şi limite |
|
Scop. Calculul deformaţiilor
torsionale (de răsucire), în general, se efectuează în scopul
preîntâmpinării funcţionărilor necorespunzătoare (cu vibraţii torsionale
şi zgomote) ale elementelor aflate pe fluxul de transmitere a
mişcării şi momentului de torsiune (fig. ARD-T.8.5).
Ipoteze simplificatoare:
- modelul
real (fig. ARD-T.8.5,a) cu arborele în trepte
(cu tronsoanele de diametru
di
şi lungime
li,
i = 1...n) se înlocuieşte cu un model echivalent
(fig. ARD-T.8.5,b) cu secţiune constantă
(cu
diametrul
de)
şi lungimea le;
-
diametrul
de
al arborelui echivalent
se consideră egal cu unul din
diametrele tronsoanelor arborelui real (de ex. de
= dj
cu j = 1, 2 sau n);
-
lungimea le a
arborelui echivalent se
determină din condiţiile egalităţilor rigidităţilor fiecărui tronson
al arborelui real cu a celui echivalent,
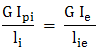 ,
(ARD-T.8.3.2.1) ,
(ARD-T.8.3.2.1)
din care, ţinând cont că momentele de
inerţie polare ale tronsoanelor i şi al tronsonului corespunzător
arborelui echivalent Ipi=
π
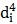 /32
şi, respectiv, Ie=
π /32
şi, respectiv, Ie=
π
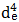 /32, rezultă lungimea
tronsonului echivalent, /32, rezultă lungimea
tronsonului echivalent,
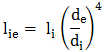 .
(ARD-T.8.3.2.2) .
(ARD-T.8.3.2.2)
Lungimea arborelui echivalent se
determină ca sumă a lungimilor tronsoanelor echivalente,
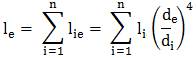 .
(ARD-T.8.3.2.3) .
(ARD-T.8.3.2.3)
Unghiul de răsucire (rotire axială)
al arborelui echivalent şi deci al arborelui real în zona solicitată la
torsiune se determină cu relaţia,
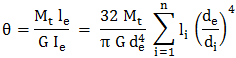 [rad],
(ARD-T.8.3.2.4) [rad],
(ARD-T.8.3.2.4)
în care, de
= dj
[mm] cu j = 1, 2 sau n;
Mt
[Nmm] - momentul de torsiune;
G [MPa] - modulul
de elasticitate transversal al materialului;
li
(i = 1...n)
[mm] - lungimile
tronsoanelor arborelui real |
|
Calculul de verificare la deformaţii de torsiune (răsucire)
constă în determinarea valorilor unghiurilor de răsucire (rotirilor
axiale) ale arborelui şi limitarea acestora la valori admisibile (θ
≤ θ
a).
Valorile admisibile pentru unghiul de
torsiune (răsucire), determinate de destinaţia arborelui,
recomandate în literatura de specialitate, sunt:
θa
≤ (15 ... 25) 10-2 rad/m, pentru arborii diferenţialelor
autovehiculelor (arborii planetari);
θa
≤ (40 ... 55) 10-4 rad/m, pentru arborii mecanismelor de
deplasare ale podurilor rulante. În cazul arborilor scurţi (reductoare
de uz general, cutii de viteze etc.), în general, rigiditatea la
torsiune nu are rol esenţial şi, ca urmare, nu este necesar calculul la
deformaţii torsionale.
În cazul în care unghiurile efective de
torsiune (răsucire) depăşesc valorile recomandate în literatura de
specialitate, se măreşte rigiditatea arborelui la torsiune, prin mărirea
diametrelor şi/sau micşorarea lungimilor tronsoanelor acestuia. |
ARD-T.8.4
Modele
de calcul la solicitări variabile (oboseală)
|
a
b
c
Fig. ARD-T.8.6 Scheme de
calcul la oboseală a arborilor: a
– schema ciclului de solicitare determinist (staţionar) b - curba
durabilitate, σ-N (Wohler) în coordonate
logaritmice;
c
– diagramele
rezistenţelor la oboseală (ciclurilor limită, pentru
R
= [-1, 1])
|
Scop,
particularităţi de calcul şi limite |
|
Scop. Calculul la solicitări variabile
(oboseală), în general, se efectuează în vederea preîntâmpinării
ruperii arborilor, cu precădere, în zona concentratorilor de
tensiune (fig. ARD-T.6.1).
Calculul obişnuit al arborilor la solicitări variabile este
de verificare la solicitări (simple sau compuse) staţionare, de regulă,
pentru durabilitate nelimitată (fig. ARD-T.8.6,b). Acest calcul se face pornind de la diagrama de
durabilitate (a ciclurilor limită a materialului,
fig. ARD-T.8.6,c) pentru care se elaborează o
diagramă schematizată, simplificată (Sodeberg, Goodman, Serensen;
fig. ARD-T.8.6,c), pe baza căreia se stabilesc relaţii de
calcul pentru coeficientul de siguranţă, ca raportul dintre rezistenţa la
oboseală a materialului (tensiunea maximă a ciclului limită,
fig. ARD-T.8.6,c;
v. Obs.,c) şi tensiunea maximă
a ciclului de solicitări variabile
(fig. ARD-T.8.6,a).
Condiţia rezistenţei la oboseală a
arborilor drepţi în zonele care există concentratori de tensiuni (canale de pană, caneluri,
salturi de diametre, găuri transversale, filet, ajustaje presate etc.;
ARD-T.8.7),
cu precădere, supuşi la solicitări compuse (torsiune şi încovoiere)
este dată de relaţia,
c ≥
ca,
(ARD-T.8.4.1)
ce presupune calculul în zonele cu
concentratori de tensiune (fig.
ARD-T.8.7)
a coeficientului de siguranţă global
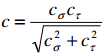 ,
(ARD-T.8.4.2) ,
(ARD-T.8.4.2)
care se determină în funcţie de
coeficienţii de siguranţă parţiali (conform schematizării
simplificată, Serensen),
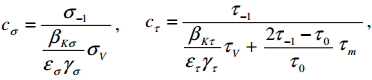 (ARD-T.8.4.3)
(ARD-T.8.4.3)
unde, σ-1,
τ-1 sunt rezistenţa la
oboseală pentru solicitarea de încovoiere, respectiv torsiune, pentru
ciclul alternant simetric; τ0
– rezistenţa la oboseală pentru solicitarea de torsiune, pentru ciclul
pulsator; τm – tensiunea medie a ciclului de solicitare la torsiune; σv,
τv – amplitudinile
ciclurilor de solicitare la încovoiere, respectiv la torsiune; βkσ,
βκτ - coeficienţi
efectivi de concentrare a tensiunilor în secţiunea considerată,
corespunzători solicitării de încovoiere, respectiv de torsiune; εσ,
ετ - coeficienţi
dimensionali, corespunzători solicitării de încovoiere, respectiv de
torsiune; γσ, γτ
- coeficienţi de calitate a
suprafeţei, corespunzători solicitării de încovoiere, respectiv de
torsiune.
Pentru coeficientul de siguranţă
admisibil, se recomandă valorile: ca
= 1,3 ... 1,5 – pentru arbori executaţi din material omogen, cu
tehnologie de execuţie corectă şi la care solicitările sunt precis
stabilite; ca
= 1,5 ... 2,5 – pentru arbori executaţi din material neomogen şi la care
solicitările sunt stabilite cu aproximaţie.
|
|
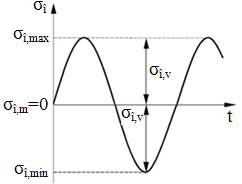
Obs.
a.
Ciclurile
de solicitare
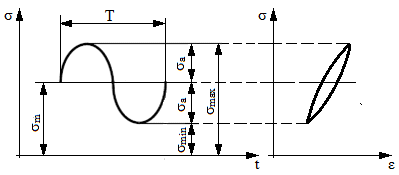
deterministe (staţionare) descrise de funcţii periodice (frecvent,
sinus) sunt caracterizate de următorii parametri caracteristici
(fig. ARD-T.8.6,a)
: tensiunea maximă, σmax;
tensiunea minimă, σmin;
tensiunea medie, σm = (σmax
+ σmin)/2;
amplitudinea ciclului, σa = (σmax
- σmin)/2;
coeficientul de asimetrie, R = σmax/σmin.
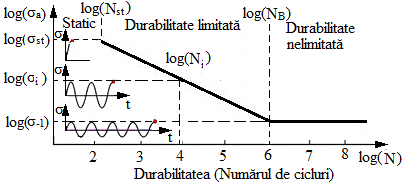
b. Stările
funcţionale
ale unui arbore din punct de vedere al rezistenţei la oboseală
sunt (fig. ARD-T.8.6,b):
cu durabilitate mică (durata de viaţă redusă, N < 102…103);
cu durabilitate (mare) limitată (102…103 <
N < 106…107); cu durabilitate (mare) nelimitată
(N > 106…107).
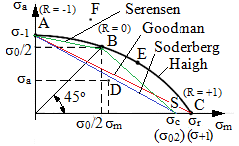
c. Ciclul
de solicitare cu coeficientul de asimetrie R şi cu tensiunea maximă σmax
egală cu rezistenţa la oboseală a materialului
(σ-1) se numeşte
ciclu limită. Efectul tensiunii medii se cuantifică cu
diagrama rezistenţelor la oboseală sau curba ciclurilor
limită (locul geometric al punctelor corespunzătoare ciclurilor
limită) care evidenţiază variaţia rezistenţei la oboseală cu
coeficientul de asimetrie, -1 < R < 1 (schematizarea Haigh,
fig. ARD-T.8.6,c).
În practică aceste diagrame permit determinarea rezistenţelor la
oboseală în funcţie de coeficienţii de asimetrie R (sau de σm
şi σa).
În fig. ARD-T.8.6,c
se prezintă diagrama High pentru solicitarea de tracţiune în care se
evidenţiază puncte corespunzătoare ciclurilor de solicitare: A –
alternat simetric, B – pulsator, C – static, E – alternant/oscilant (-1
< R < 1).
c.
Coeficienţii
βkσ,
βκτ,
γσ,
γτ,
εσ,
ετ
sunt coeficienţi de corecţie, care ţin seama de faptul că încercările
la oboseală ale materialelor se fac pe epruvete standard care se execută
fără concentratori de tensiuni şi ale căror dimensiuni şi prelucrări
diferă de cele ale arborilor proiectaţi (fer. ARD-P.1). Coeficienţii
βkσ,
βκτ, se
definesc ca raport între rezistenţa la oboseală a epruvetei lustruite,
fără concentrator, şi rezistenţa la oboseală a epruvetei cu aceleaşi
dimensiuni ca cea netedă dar prevăzută cu concentrator, pentru acelaşi
ciclu de
solicitare; valorile acestora se aleg din diagrame, în funcţie de tipul
şi caracteristicile concentratorului (fer. ARD-P.1). Coeficienţii εσ
şi ετ ţin seama de faptul că dimensiunile reale ale arborelui
diferă de cele ale epruvetei, valorile acestora fiind date în diagrame
şi sunt cuprinse în intervalul 1,4 ... 19 (fer. ARD-P.1). Coeficienţii γσ
şi γτ se definesc ca raport între rezistenţa la oboseală a
epruvetei cu suprafaţă rugoasă şi rezistenţa la oboseală a epruvetei cu
suprafaţa lustruită (fer. ARD-P.1).
c.
În cazul în care
într-o anumită secţiune condiţia impusă prin relaţia (ARD-T.8.4.1) nu este
îndeplinită, se iau măsuri constructive pentru îndeplinirea ei
prin introducerea de concentratori care induc tensiuni locale mult
reduse
(fig.
ARD-T.8.6): trecere de secţiune (salturile de diametre,
fig.
ARD-T.8.6,a...l);
canal de pană sau caneluri
(fig.
ARD-T.8.6,m,n,o); modificator al
presiunii de capăt, din zonele de contact arbore – organe susţinute
(fig.
ARD-T.8.6,p...t); filet, se recomandă folosirea filetului la capete de arbori, unde
momentele încovoietoare sunt reduse şi/sau folosirea filetelor cu pas fin. |
 |
 |
 |
 |
 |
|
a |
b |
c |
d |
e |
|
|
|
 |
 |
 |
|
f |
g |
h |
i |
j |
|
 |
 |
 |
 |
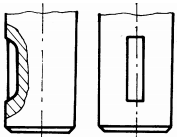 |
|
k |
l |
m |
n |
o |
|
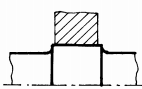 |
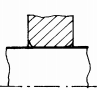 |
 |
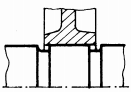 |
 |
|
p |
q |
r |
s |
t |
|
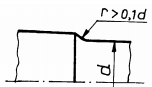
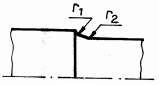
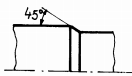
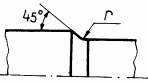
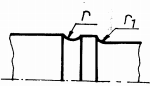
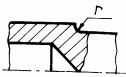
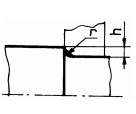
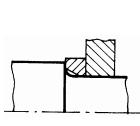
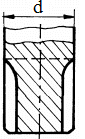
Fig. ARD-T.8.7
Măsuri
constructive pentru mărirea rezistenţei la oboseală:
a –
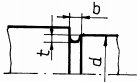
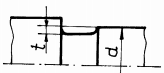
rază de racordare (în cazul când diferenţa între trepte este mică); b -
două raze de racordare diferite (în cazul arborilor foarte solicitaţi);
c -
teşirea capătului treptei de diametru mare (pentru salturi mici de
diametre); d -
teşirea capătului treptei de diametru mare, combinată cu racordare la
treapta de diametru mic (pentru salturi mari de diametre);
e -
rază de racordare, combinată cu canal de descărcare pe treapta de diametru
mare; f -
rază de racordare, combinată cu executarea unei găuri pe treapta de diametru
mare; g -
canal de trecere scurt, executat la capătul treptei de diametru mic (la
arbori de dimensiuni mici); h
-
canal de trecere lung, executat la capătul treptei de diametru mic (la
arbori de dimensiuni mari); i
-
degajare interioară, executată în treapta de diametru mare (în cazul
abaterilor reduse de perpendicularitate); j
-
canal de trecere combinat cu degajare interioară (soluţia asigură
creşterea rezistenţei la oboseală, accesul pietrei de rectificat pe toată
lungimea tronsonului de diametru mic şi un sprijin axial corect al organelor
montate pe arbore); k
-
rază de racordare mare care necesită teşirea piesei conjugate;
l -
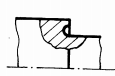
folosirea de piese (inele) intermediare; m
- caneluri
(rezistenţă la oboseală mai mare decât în cazul canalelor de pană);
n
-
canalele de pană cu capetele rotunjite (deoarece nu asigură rezistenţe la
oboseală mărite se recomandă să se poziţioneze spre capetele arborilor);
o -
canale de pană cu capetele drepte (rezistenţă la oboseală mărită, se
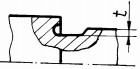
poziţionează în zonele centrale ale arborilor); p
-
îngroşarea porţiunii de calare; q
-
teşirea sau rotunjirea muchiilor butucului; r - configurarea roţii cu disc
(pentru roţile cu diametre mari); s -
executarea canalelor de descărcare în arbore; t -
executarea canalelor de descărcare în butuc |
ARD-T.8.5 Modele
de calcul la vibraţii
Scopul calculului la
vibraţii este prevenirea
ruperii arborelui din cauza eforturilor mult mărite care apar la intrarea
subansamblului acestuia în rezonanţă. Calculul constă în
determinarea turaţiei critice a arborelui şi compararea acestuia cu turaţia de
funcţionare.
Turaţia critică este turaţia
la care arborele intră în rezonanţă ca urmare a situaţiei în care frecvenţa (pulsaţia)
proprie coincide sau este multiplu al frecvenţei forţelor perturbatoare
Frecvenţa (pulsaţia) proprie
este o caracteristică a unui sistem oscilant independentă de condiţiile iniţiale
ale mişcării.
În funcţie de tipul forţelor
perturbatoare se întâlnesc vibraţii flexionale (transversale, de încovoiere), torsionale şi/sau
longitudinale (la arborii verticali unde apar sarcini axiale variabile).
ARD-T.8.5.1
Model de calcul la vibraţii transversale
(flexionale)
Vibraţiile flexionale (transversale)
sunt cauzate de erorile de execuţie şi montaj ale arborelui şi ale elementelor
montate pe acesta, de neomogenităţile materialului şi de deformaţia elastică a
acestuia sub acţiunea forţelor exterioare.
|
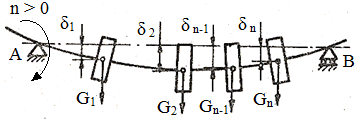
a 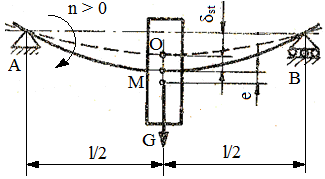
b 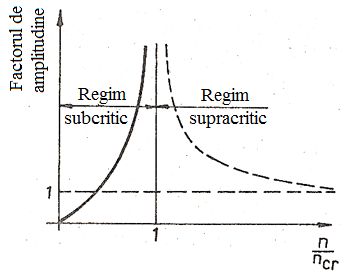
c
Fig. ARD-T.8.8 Model de
calcul la vibraţii flexionale: a –
cazul general cu n discuri; b - caz particular cu un disc simetric;
c
- regimurile de funcţionare
|
Model de calcul la
vibraţii flexionale |
|
Ipoteze
simplificatoare:
- subansamblul arbore se consideră compus
din arbore cu masa neglijabilă şi n discuri (roţi dinţate, roţi de
curea, volanţi etc.) montate pe arbore care au masele mi,
i = 1...n;
- din cauza erorilor de execuţie şi montaj
şi a neomogenităţilor materialelor centrele de masă ale discurilor sunt
excentrice (fig. ARD-T.8.8,
b) şi în timpul rotaţiei arborelui (n > 0) apar forţe centrifuge (de
excitaţie) ce conduc la oscilaţii transversale;
- fibra medie deformată (fig. ARD-T.8.8,
a), în stare de repaus (n = 0), reprezintă limita extremă a
deformaţiilor care iau naştere în timpul rotirii şi este determinată de
săgeţile δi
produse de greutăţile, Gi
= mi
g (g, acceleraţia gravitaţonală);
- considerând vibraţiile armonice,
săgeţile transversale variază în timp conform relaţie, δti =
δi
sin ωt;
- vitezele de mişcare a centrelor
discurilor,
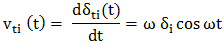
au valorile maxime, vi
= ω δi.
Relaţii de calcul:
Din condiţia de egalare a energiei
potenţiale maxime (corespunzătoare fibrei medii deformate extremă unde
energia cinetică este nulă) cu energia cinetică maximă (corespunzătoare
fibrei medii deformate mediane, linia AB, unde energia potenţială este
nulă) a subansamblului arborelui,
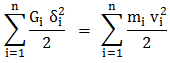 ,
(ARD-T.8.5.1) ,
(ARD-T.8.5.1)
considerând ipotezele simplificatoare,
rezultă viteza unghiulară
[rad/s]
(turaţia [rot/min]) critică (la care apare rezonanţa),
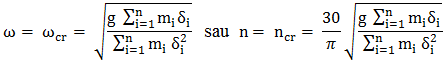 ,
(ARD-T.8.5.2) ,
(ARD-T.8.5.2)
unde, mi
[kg] sunt masele
discurilor, g [mm/s2] - acceleraţia gravitaţională, δi
[mm] - săgeţile arborelui în zonele
discurilor.
Pentru cazul particular, al
arborelui cu un singur disc (fig. ARD-T.8.8,
b) montat
simetric pe arbore, aceste relaţii devin,
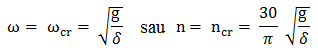 .
(ARD-T.8.5.3) .
(ARD-T.8.5.3)
Considerând, pentru acest caz, în
relaţia de mai sus,
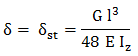 ,
(ARD-T.8.5.4) ,
(ARD-T.8.5.4)
rezultă, relaţia turaţiei critice,
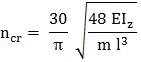 ,
(ARD-T.8.5.5) ,
(ARD-T.8.5.5)
unde, E [MPa] este modulul de
elasticitate longitudinală al materialului arborelui; Iz
[mm4]
- momentul de inerţie axial al secţiunii arborelui; m [kg] -
masa discului montat pe arbore; l [mm] - lungimea arborelui |
|
Regimurile
de funcţionare:
a.
n/ncr
< 1 (n < ncr), regimul subcritic
(fig.
ARD-T.8.8,c),
corespunzător arborilor rigizi;
b.
n/ncr
>
1 (n > ncr), regimul supracritic (fig.
ARD-T.8.8,c)
corespunzător arborilor elastici (există tendinţa de
autocentrare); se recomandă trecerea peste turaţia critică să se
facă rapid şi/sau adoptarea de măsuri constructive de limitarea
amplitudinilor vibraţiilor la rezonanţă.
Obs.
Se recomandă evitarea domeniului din
zona de rezonanţă, n/ncr
= 0,85…1,25
în
care creşterea deformaţiilor (săgeţilor) este foarte mare |
ARD-T.8.5.2
Model de calcul a la vibraţii torsionale
ARD-T.9 MODELE DE CALCUL A
OSIILOR
|
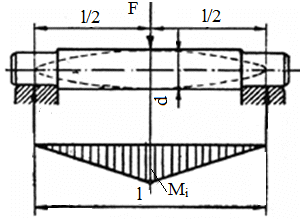
Fig. ARD-T.8.9 Schema de
calcul a unei osii |
Particularităţi de calcul
a osiilor |
|
Sub acţiunea sarcinilor exterioare osiile, în majoritatea situaţiilor,
sunt solicitate la încovoiere.
Din condiţia de
rezistenţă la încovoiere,
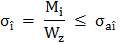 ,
(ARD-T.8.9.1) ,
(ARD-T.8.9.1)
se determină relaţia de
dimensionare,
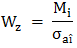 ,
(ARD-T.8.9.2) ,
(ARD-T.8.9.2)
din care se determină
diametrul osiei în zona mediană,
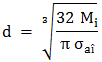 (ARD-T.8.9.3)
(ARD-T.8.9.3) |















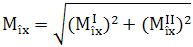
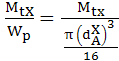
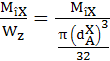
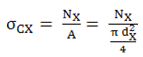
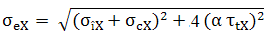
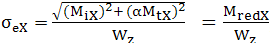
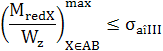
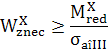
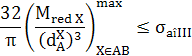
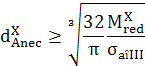









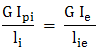 ,
,
 /32
/32 /32, rezultă lungimea
tronsonului echivalent,
/32, rezultă lungimea
tronsonului echivalent, 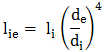 .
.
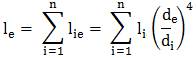 .
.
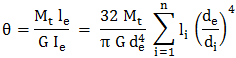 [rad],
[rad], 


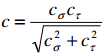 ,
(ARD-T.8.4.2)
,
(ARD-T.8.4.2)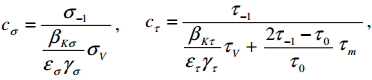 (ARD-T.8.4.3)
(ARD-T.8.4.3)






















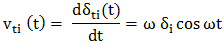
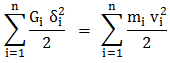 ,
(ARD-T.8.5.1)
,
(ARD-T.8.5.1)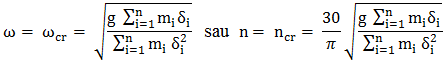 ,
(ARD-T.8.5.2)
,
(ARD-T.8.5.2)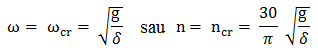 .
.
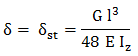 ,
,
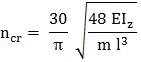 ,
(ARD-T.8.5.5)
,
(ARD-T.8.5.5)
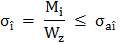 ,
(ARD-T.8.9.1)
,
(ARD-T.8.9.1)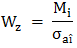 ,
(ARD-T.8.9.2)
,
(ARD-T.8.9.2)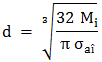 (ARD-T.8.9.3)
(ARD-T.8.9.3)