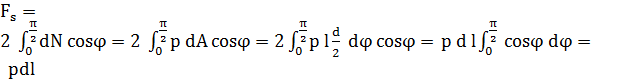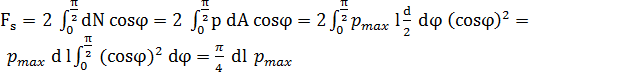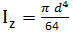PRC-T PROIECTAREA CONSTRUCTIVĂ A ELEMENTELOR PRODUSELOR TEHNICE MECANICE

 

PRC-T.3  CALCULUL DE REZISTENŢĂ ŞI DE RIGIDITATE (DEFORMAŢII) A ELEMENTELOR MAŞINILOR

 

 

            CUPRINS

PRC-T.3.1  CALCULUL DE REZISTENŢĂ AL ELEMENTELOR MAŞINILOR

PRC-T.3.1.1  STRUCTURA GENERALĂ A SISTEMELOR DE CORPURI ÎN INTERACŢIUNE

PRC-T.3.1.2  MODELAREA GEOMETRICĂ A ELEMENTELOR STRUCTURILOR MECANICE

PRC-T.3.1.3  MODELAREA LEGĂTURILOR (REAZEMELOR) DINTRE CORPURI

PRC-T.3.1.4  MODELAREA SARCINILOR

PRC-T.3.1.4.1 MODELAREA SARCINILOR EXTERIOARE (ÎNCĂRCĂRILOR)

PRC-T.3.1.4.2 MODELAREA SARCINILOR INTERIOARE (EFORTURILOR)

PRC-T.3.1.5  MODELAREA SOLICITĂRILOR

PRC-T.3.1.5.1 MODELAREA SOLICITĂRILOR  DE VOLUM                

PRC-T.3.1.5.1.1 Modelarea solicitărilor  de volum simple

PRC-T.3.1.5.1.2 Modelarea solicitărilor  de volum compuse

PRC-T.3.1.5.2 MODELAREA SOLICITĂRILOR  DE SUPRAFAŢĂ

PRC-T.3.1.5.2.1  Modelarea solicitărilor  de strivire pe suprafaţe conforme plane

PRC-T.3.1.5.2.2 Modelarea solicitărilor de strivire pe suprafaţele conforme cilindrice  

PRC-T.3.1.6 TENSIUNI ADMISIBILE ŞI COEFICIENŢI DE SIGURANŢĂ

PRC-T.3.2  CALCULUL DE RIGIDITATE (DEFORMAŢII) AL ELEMENTELOR MAŞINILOR

PRC-T.3.2.1 MODELAREA DEFORMAŢIILOR  ŞI  DEPLASĂRILOR DE VOLUM

PRC-T.3.2.2 DEPlASĂRI ADMISIBILE ŞI COEFICIENŢI DE SIGURANŢĂ

 

PRC-T.3.1  CALCULUL DE REZISTENŢĂ AL ELEMENTELOR MAŞINILOR

 

 PRC-T.3.1.1  STRUCTURA GENERALĂ A SISTEMELOR DE CORPURI ÎN INTERACŢIUNE

 

 

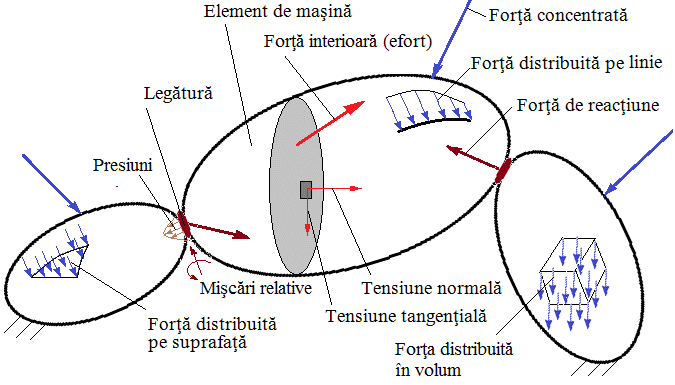
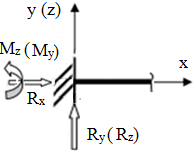
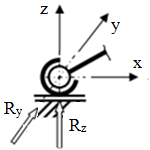
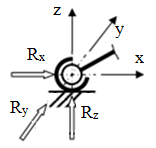
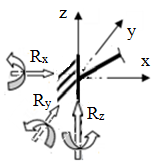
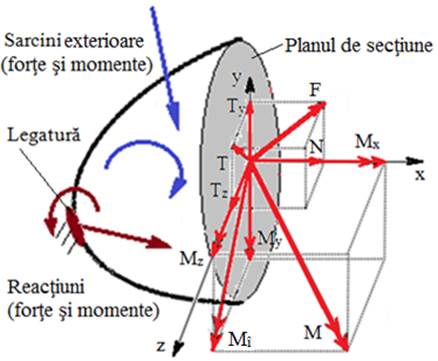
Aspecte generale despre structurile funcţionale ale produselor mecanice:

-         corpurile care îndeplinesc rol funcţional de transmitere de forţe (sarcini) în cadrul unei structuri mecanice a unui produs (maşină, instalaţie, utilaj etc.) şi sunt supuse la diverse solicitări, sunt cunoscute sub denumirea de elemente de rezistenţă sau elemente (organe) de maşină;

-         elementele maşinilor sunt în interacţiune prin intermediul legăturilor (fixe sau mobile) care se idealizeză prin reazeme şi cuple cinematice şi se materializeză prin diverse soluţii constructive (asamblări, îmbinări, lagăre etc.);

-         în reazeme şi cuple cinematice pot exista mişcări relative şi forţe de reacţiune;

-         elementele maşinilor pot fi încărcate cu sarcini exterioare, forţe şi/sau momente, concentrate sau distribuite (pe linie, pe suprafaţă şi/sau în volum);

-         consecinţă a acţiunii încărcărilor (sarcinilor) externe şi interne în interiorul corpurilor apar tensiuni (normale şi/sau tangenţiale) şi pe suprafeţele presiuni de contact;

-         tensiunile din elementele constructive se însumează în punctele din interior în  forţe interioare (eforturi) şi în punctele suprafeţelor de contact din reazeme în forţe de reacţiune

Fig. PRC-T.3.1.1.1  Modelul  general al unui sistem de corpuri în interacţiune

 

PRC-T.3.1.2 MODELAREA GEOMETRICĂ A ELEMENTELOR STRUCTURILOR MECANICE

 

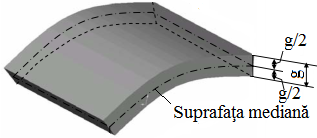
Elementele constructive ale produselor mecanice, ţinând cont de raportul dintre dimensiunile lor, se pot reduce (simplifica) la  trei categorii: bare (rigide sau flexibile), cu o dimensiune mult mai mare în comparaţie cu celelalte două; plăci  cu două dimensiuni mult mai mari decât cea de-a treia; elemente masive (blocuri) cu cele trei dimensiuni comparabile (bile, roţi, flanşe, tuburi cu pereţi groşi, volanţi etc.).

 

Tab. PRC-T.3.1.2.1  Clasificarea elementelor constructive de tip bară

Criteriul

Tipul

Schema

Descriere

Forma fibrei medii (locul geometric al centrelor de greutate ale formelor secţionale)

Drepte

Fig. PRC-T.3.1.2.2,a

Se materializează ca arbori, bolţuri, şuruburi etc.

Cotite

Fig. PRC-T.3.1.2.2,b

Se materializează ca arbori cotiţi

Curbe

Fig. PRC-T.3.1.2.2,c,d

Se materializează ca elemente rigide (cârligul de remorcare) sau flexibile

Forma secţiunii transversale

Cu secţiune plină

Fig. PRC-T.3.1.2.1,a

Pot fi cu secţiune circulară, pătrată, dreptunghiulară hexagonală etc.

Cu secţiune deschisă

Fig. PRC-T.3.1.2.1,b

Pot fi cu ptofil semcircular, U, I, L etc.

Cu secţiune cu goluri

Fig. PRC-T.3.1.2.1,c

Cu profil circular, pătrat, dreptunghiular, compus din forme simple etc.

Tipul solicitării principale

Tiranţi

Fig. PRC-T.3.1.2.1,a

Solicitarea principală este tracţiunea (întinderea)

Sarme, cabluri

Fig. PRC-T.3.1.2.1,d

Stâlpi (coloane)

Fig. PRC-T.3.1.2.1,b

Solicitarea principală este compresiunea

Grinzi

Fig. PRC-T.3.1.2.1,c

Solicitarea principală este încovoierea

Arbori

Fig. PRC-T.3.1.2.1,a,b

Solicitările principale pentru arborii rigizi sunt: torsiunea şi încovoierea

 

 

a

b

c

Fig. PRC-T.3.1.2.1 Formele secţiunilor barelor: a – plină; b – deschisă; c  – tubulară (ţeavă)

 

a

b

c

d

Fig. PRC- PRC-T.3.1.2.2 Formele fibrelor medii ale barelor: a – dreaptă (arbore drept); b – cotită (arbore cotit); c  – curbă, rigidă; d  – curbă, flexibilă (cablu);

 

 

a

b

c

d

Fig. PRC- PRC-T.3.1.2.3 Exemple de elemente constructive de tip bară: a – tirant; b – coloană (stâlp); c  – grindă; d  – bară spaţială

                           

Tab. PRC-T.3.1.2.2  Clasificarea elementelor constructive de tip placă

Criteriul

Tipul

Schema

Descriere

Forma suprafeţei mediane 

Plane

Fig. PRC-T.3.1.2.4

Suprfaţa mediană este plană

Curbe

Suprfaţa mediană este spaţială

Grosimea

Membrane (plăci subţiri)

Au grosimi mici şi nu preiau forţe transversale

Învelitori

Au grosimi foarte mici şi nu preiau momente de încovoiere

Dale (plăci groase)

Au grosimi mari şi dimensiuni ale  suprafaţei mediane reduse

 

Fig. PRC-T.3.1.2.4 Descrierea  plăcilor

 

PRC-T.3.1.3 MODELAREA LEGĂTURILOR (REAZEMELOR) DINTRE CORPURI

 

Legăturile modelează interacţiunile  dintre două elemente constructive prin reazeme  care, la rândul lor, sunt materializate prin elemente sau subansamble de legătură (asamblări, lagăre, îmbinări) specifice sau specializate; Legăturile pot fi fixe, fără mişcări relative (numai cu reacţiuni) sau mobile, cu mişcări relative (cuple cinematice în care apar reacţiuni în direcţia mişcărilor anulate.

 

Tab. PRC-T.3.1.3.1  Clasificarea reazemelor

Criteriul

Tipul

Schema

Descriere

Domeniul geometric

Plane

Fig. PRC-T.3.1.3.1,a,b,c,d

Deplasările şi rotirile după una din axele transversale sunt nule; rigidităţile elementelor în această direcţie sunt infinite

Spaţiale

Fig. PRC-T.3.1.3.1,e,f,g

Pot fi rigide sau elastice

Gradele de mobilitate anulate

Cu o constrângere

Fig. PRC-T.3.1.3.1,a,b

Permit 5 mişcări relative în cazul reazemelor spaţiale şi 2 pentru cele plane

Cu 2 constrângeri

Fig. PRC-T.3.1.3.1,c,e

Permit 4 mişcări relative în cazul reazemelor spaţiale şi una pentru cele plane

Cu 3 constrângeri

Fig. PRC-T.3.1.3.1,d,f

Permit 3 mişcări relative în cazul reazemelor spaţiale

Cu 4 constrângeri

-

Permit 2 mişcări relative în cazul reazemele spaţiale

Cu 5 constrângeri

-

Permit o mișcare relativă pentru reazemele spaţiale

Cu 6 constrângeri

Fig. PRC-T.3.1.3.1,g

Nu permit mişcări relative (sunt materializate de asamblările şi îmbinările nedemontabile)

Rigiditaea elementelor rezemate

Rigide

Fig. PRC-T.3.1.3.1,b … g

Nu se iau în considerare deformaţiile elastice din legături

Elastice

Fig. PRC-T.3.1.3.1,a

Se iau în considerare deformaţiile elastice prin intermediul unor elemente elastice

 

 

a

b

c

d

e

f

g

Fig. PRC-T.3.1.3.1 Tipuri uzuale de reazeme: a – reazem elastic mobil plan; b – reazem mobil plan; c – reazem  fix plan (articulaţie cilindrică) ; d – încastrare plană; e – reazem mobil spaţial; f – reazem fix spaţial (articulaţie sferică); g – încastrare spaţială

 

PRC-T.3.1.4 MODELAREA ÎNCĂRCĂRILOR (SARCINILOR)

 

PRC-T.3.1.4.1 MODELAREA SARCINILOR EXTERIOARE (ÎNCĂRCĂRILOR)

 

Tab. PRC-T.3.1.4.1.1  Clasificarea sarcinilor exterioare  

Criteriul

Tipul

Schema

Descriere

Domeniul în care acţionează 

Exterioare  (sarcini)

Fig. PRC-T.3.1.4.1

Sarcinile exterioare sunt rezultatul acţiunii unor câmpuri fizice (mecanice, termice, electromagnetice)

Interioare (eforturi)

Fig. PRC-T.3.1.4.2

Acţionează în interiorul corpurilor şi se determină prin însumarea tensiunilor interne

De legătură (reacţiuni)

Fig. PRC-T.3.1.3.1

Acţionează ca forţe de reacţiune şi se determină prin însumarea presiunilor de pe suprafeţele în contact

Suportului pe care acţionează

În punct (concentrat)

Fig. PRC-T.3.1.1.1

Acționează pe suprafeţe foarte mici ce se pot reduce, teoretic, la un punct

Pe linie

Acționează pe o suprafaţă cu lungime mare şi îngustă ce se poate reduce la o linie

Pe suprafaţă

Acționează pe suprafeţe exterioare şi interioare ale elementelor constructive

În volum

Pot acţiona, rareori, numai în anumite părţi ale volumului corpului  sau, frecvent, în tot volumul (forţe de greutate, centrifugă, electromagnetică etc.)

Distribuţiei pe suportul care acţionează

Distribuite uniform

Fig. PRC-T.3.1.1.1

Sunt valabile pentru sarcinile aplicate pe contururi, suprafeţe şi volume

Distribuite neuniform

Modul de aplicare în timp

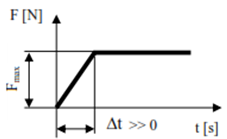
Statice

Fig. PRC-T.3.1.4.1,a

Se consideră aplicate lent şi nu implică efecte dinamice

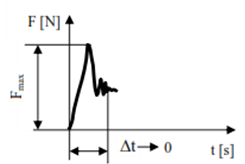
Dinamice aplicate brusc (cu şoc)

Fig. PRC-T.3.1.4.1,d

Sunt aplicate în timpi scurţi şi se consideră efectele dinamice (inerţiale)

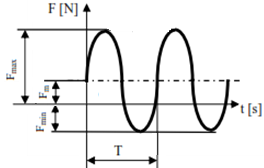
Variabile periodic

Fig. PRC-T.3.1.4.1,b

Variaţiile în timp, periodice pulsatorii sau alternante, au efecte asupra rezistenţei la oboseală în perioade de funcţionare mărite (durabilitate)

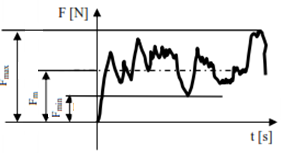
Variabile aleatoriu

Fig. PRC-T.3.1.4.1,c

Variaţiile în timp, aleatorii, au efecte asupra rezistenţei la oboseală în perioade de funcţionare mărite (durabilitate)

Mobilitatea suportului pe care acţionează

Fixe

-

Acţiunea acestor sarcini rămâne invariabilă (calcule de rezistenţă liniare)

Mobile

-

Pentru calcule de proiectare, din toate stările posibile de încărcare, se consideră cea care produce încercarea cea mai defavorabilă

Obs.  Reacţiunile din reazeme (fig.   PRC-T.3.1.3.1), ca sarcini exterioare indirecte, frecvent, se modelează ca forţe şi momente concentrate

 

a

b

c

d

Fig. PRC-T.3.1.4.1.1  Tipurile sarcinilor exterioare (forţe sau momente): a – statică; b – variabilă periodic; c – variabilă aleatoriu; d – cu şoc;

 

 

PRC-T.3.1.4.2 MODELAREA SARCINILOR INTERIOARE (EFORTURILOR)

 

Tab. T.3.1.4.1.2  Clasificarea eforturilor secţionale

Criteriul

Tipul efortului

Descriere

Poziţia în raport cu planul de secţiune

Normal (axial)

N, Mx - au direcţia după axa x, normală pe planul de secţiune

Tangenţial

Ty,z, My,z, T, Mî - au direcţia în planul de secţiune, y-z

Solicitările asociate

De tracţiune/compresiune

N – efort axial de tracţiune/compresiune

De forfecare

Ty,z – eforturi de forfecare,

 – efort de forfecare rezultant

 

De torsiune (axial)

Mx – efort axial de torsiune;

De încovoiere

My,z – eforturi de încovoiere,

 – efort de încovoiere rezultant

 

Luarea în considerare ca şi componentă sau ca rezultantă

Parţial (componentă)

Ty,z, Mx,y,z – componentele eforturilor T şi M

Rezultant

  - forţa interioară

 

  - momentul interior

 

Fig. PRC-T.3.1.4.2.1  Componentele eforturilor secţionale

 

            

PRC-T.3.1.5 MODELAREA SOLICITĂRILOR

 

   Ipotezele calculelor de rezistenţă:

-         continuităţii, conform căreia corpurile se consideră continue făcând abstracţie de structura sa cristalină;

-         izotropiei, conform căreia materialele au aceleaşi proprietăţi după oricare direcţie, (care trece printr-un anumit punct);

-         omogenităţii, corpurile considerându-se omogene, cu aceleaşi proprietăţi;

-         micilor deplasări, conform căreia deplasările diferitelor puncte ale corpului sunt mult mai mici în comparaţie cu dimensiunile sale;

-         elasticităţii perfecte, conform căreia corpurile revin la forma iniţială după încetarea încărcării exterioare;

-         dependenţei liniare dintre forţă şi deplasare F= k δ, unde  k = constantă (rigiditate);

-         suprapunerii de efecte, conform căreia starea finală de echilibru nu depinde de ordinea de aplicare a sarcinilor;

-         constanţei secţiunii transversale, pentru simplificarea relaţiilor de calcul;

-         solicitărilor neglijabie, pentru simplificarea relaţiilor de calcul se omit solicitările care se dovedesc nesmnificative;

-         lui Saint-Venant, conform căruia într-o secţiune depărtată de zona de încărcare a corpului, solicitarea nu depinde de modul încărcării;

-         lui Bernoulli conform căreia o secţiune plană şi normală pe axa elementului de rezistenţă rămâne plană şi normală şi pe axa sa deformată

 

Tab. PRC-T.3.1.5.1  Clasificarea solicitărilor  mecanice                        

Criteriul

Tipul solicitării

Schema

Descriere

Domeniul geometric în care se manifestă

De volum

Tab. PRC-T.3.1.5.1

Fac obiectul de studiu al rezistenţei materialelor

De suprafaţă

Tab. PRC-T.3.1.5.2

Fac obiectul de studiu al rezistenţei materialelor şi  tribologiei

După numărul de eforturi într-o secţiune

Simple

Tab. PRC-T.3.1.5.1.1.1

Au un singur efort (solicitări simple)

Compuse

Tab. PRC-T.3.1.5.1.2.1

Au cel puţin două eforturi (solicitări compuse)

 Tipul sarcinii

Statice

Fig. PRC-T.3.1.4.1.1,a

Sarcina se aplică lent şi se consideră independentă de timp

Dinamice

Fig. PRC-T.3.1.4.1.1,d

Sarcina este variabilă în timp; se consideră pentru perioade de timp reduse (foarte scurte), de obicei, pentru calcule în regimuri tranzitorii (şoc sau impact)

Variabile

Fig. PRC-T.3.1.4.1.1,b,c

Sarcina este variabilă în timp (periodic sau aleatoriu);  se consideră perioade de timp îndelungate (comparabile cu durata de viaţă a produsului),  pentru calculul la oboseală; în funcţie de material cedările (ruperile) se produc la tensiuni mai mici decât tensiunea corespunzătoare limitei de curgere (rupere) pentru solicitarea statică

    

PRC-T.3.1.5.1 MODELAREA SOLICITĂRILOR  DE VOLUM

                    

PRC-T.3.1.5.1.1 Modelarea solicitărilor  de volum simple

 

Solicitările simple sunt determinate de un singur efort.

 

Tab. PRC-T.3.1.5.1.1.1  Solicitări mecanice simple

Solicitarea

Schema

Modelul matematic

Semnificaţiile parametrilor

Scop

Relaţii de calcul

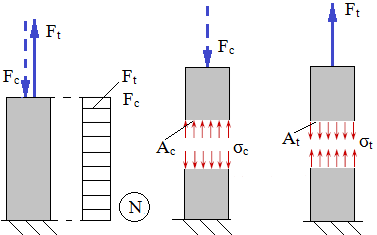
Tracţiune, compresiune

Verificare

 

Ft,c [N] –  forţa de tracţiune, compresiune;

At,c [mm2] – aria secţiunii barei solicitată la tracţiune, compresiune;

σt,c [MPa] –  tensiunea de tracţiune, compresiune maximă;

σat,c [MPa] –  tensiunea admisibilă de tracţiune, compresiune;

Ft,c cap [N] –  forţa de tracţiune, compresiune capabilă

Dimensionare

 

Sarcina capabilă

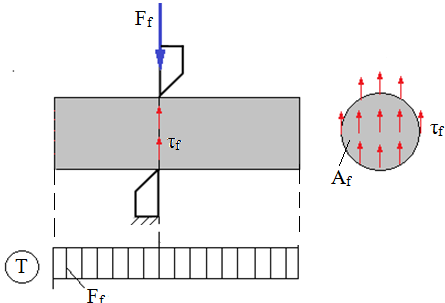
Forfecarea (tăierea) pură

Verificare

 

Ff [N] –  forţa de forfecare;

 

Af [mm2] –  aria secţiunii de forfecare;

 

τf [MPa] –  tensiunea de forfecare maximă;

 

τaf [MPa] –  tensiunea admisibilă de forfecare;

 

Ff cap [N] –  forţa de forfecare capabilă

Dimensionare

 

Sarcina capabilă

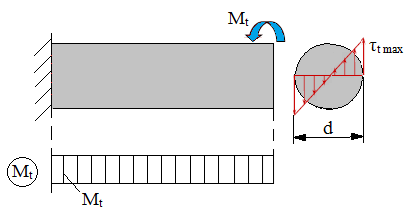
Torsiunea (răsucirea)

Verificare

 

Mt [Nmm] –  momentul de torsiune (răsucire);

Wp [mm3] –  modulul de rezistenţă polar;

, pentru secţiune circulară;

 

τt max [MPa] –  tensiunea de torsiune maximă;

τat [MPa] –  tensiunea admisibilă de torsiune;

Mt cap [Nmm] –  momentul de torsiune capabil

Dimensionare

 

Sarcina capabilă

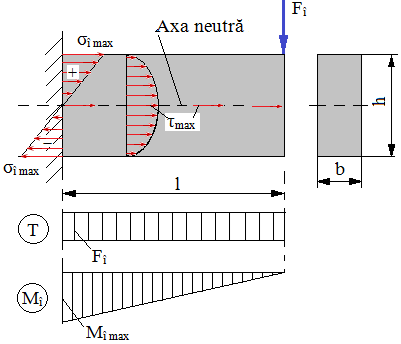
Încovoierea

Verificare

,

 

Mî max [Nmm] –  momentul de încovoierre maxim;

Fî  [N] –  forţa de încovoierre;

Wz [mm3] –  modulul de rezistenţă axial;

 , pentru secţiune circulară;

 

  , pentru secţiune dreptunghiulară;

 

σî max [MPa] –  tensiunea de încovoiere maximă, din relaţia lui Navier;

τ max [MPa] –  tensiunea de forfecare maximă, din relaţia lui Juravski;

A = b h  [mm2] – aria secţiunii barei;

σaî  [MPa]  –  tensiunea admisibilă de încovoiere;

Mî cap [MPa] –  momentul de încovoiere capabil

Dimensionare

,

Sarcina capabilă

 

 

PRC-T.3.1.5.1.2 Modelarea solicitărilor  de volum compuse

 

Solicitările compuse sunt determinate de două sau mai multe tensiuni.

 

Tab. PRC-T.3.1.5.1.2.1  Clasificarea solicitărilor compuse

Criteriul

Tipul

Schema

Descriere

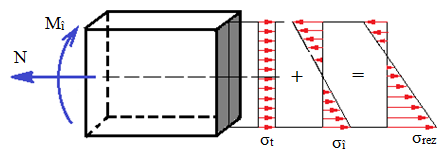
Tipul tensiunilor participante

De aceeaşi natură (σ sau τ) cu direcţii paralele

Fig. PRC-T.3.1.5.1.2.1

Dacă tensiunile au aceeaşi direcţie, tensiunea rezultantă se calculează ca suma algebrică a tensiunilor componente,

,          (PRC-T.3.1.5.1.2.1) 

 

Solicitări posibile: axială excentrică, încovoiere oblică, axială (întindere sau compresiune) şi încovoiere; forfecare cu torsiune (răsucire)

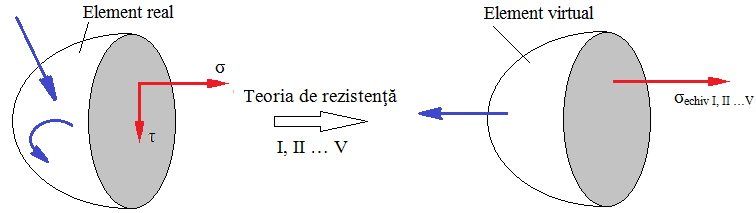
De  natură diferită (σ şi τ)  cu direcţii diferite

Fig. PRC-T.3.1.5.1.2.2

În acest caz se impune determinarea unei tensiuni echivalente  care apare într-un element imaginar (virtual) supus la întindere, din acelaşi material, şi care produce o stare de solicitare cu tensiunea σ tot atât de periculoasă (echivalentă) ca şi cea reală cu tensiuni σ şi τ.

Tensiunea echivalentă se determină, pe baza unor criterii de echivalare numite teorii de rezistenţă (tab.  PRC-T.3.1.5.1.2.2) şi se compară cu tensiuni admisibile  (PRC-T.3.1.5.1.2.1)  bazate pe tensiuni limită, uşor de determinat experimental. Solicitări compuse posibile: încovoiere şi răsucire; tracţiune, încovoiere şi răsucire

 

 

Fig. PRC-T.3.1.5.1.2.1  Însumarea  tensiunilor de aceeaşi natură (σ)

Fig. PRC-T.3.1.5.1.2.2 Echivalarea stărilor de tensiuni compuse

 

Tab. PRC-T.3.1.5.1.2.2  Teorii de rezistenţă

Nr. teoriei

Ipoteza de echivalare

Relaţia de echivalare

Descriere

1

Tensiunea normală maximă

       (PRC-T.3.1.5.1.2.1) 

S-a confirmat experimental în cazul ruperii materialelor fragile solicitate la tracţiune; în cazul stărilor compuse de tensiuni conduce la supradimensionări

2

Deformaţiei liniare maxime

 (PRC-T.3.1.5.1.2.2) 

             

Se recomandă pentru materiale fragile

3

Tensiunii tangenţiale maxime

                     (PRC-T.3.1.5.1.2.3)

              

S-a verificat experimental pentru materialele tenace la solicitările de întindere simple şi mixte; această teorie este cea mai acoperitoare, conduce la diferenţe (dimensiuni) mai mari şi se foloseşte frecvent pentru calculele de proiectare.

4

Energiei de deformaţie

                  (PRC-T.3.1.5.1.2.4)

               

-

6

Energiei de deformaţie modificatoare de formă

        (PRC-T.3.1.5.1.2.5)               

A fost verificată experimental pentru materialele tenace şi corespunde mai bine cu realitatea decât toate celelalte teorii; această teorie are o largă utilizare în proiectare deoarece conduce la diferenţe mai mici (dimensiuni apropiate de cele necesare)

 

PRC-T.3.1.5.2 MODELAREA SOLICITĂRILOR  DE SUPRAFAŢĂ

 

PRC-T.3.1.5.2.1  Modelarea solicitărilor de strivire pe suprafețe conforme plane

 

Tab. PRC-T.3.1.5.2.1.1  Calculul la strivire a suprafeţelor  conforme plane

    

 

 

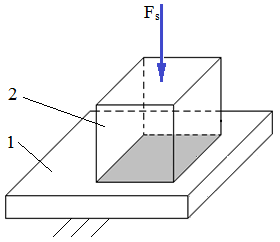
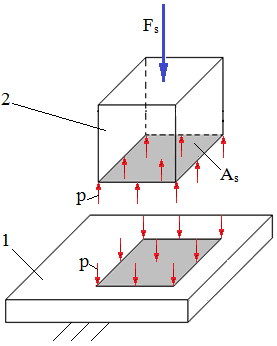
Ipoteze de calcul:

-         presiunea pe suprafaţa de contact se consideră uniform distribuită;

-         forţa se aplică perpendicular pe planul de contact

Condiţia de echilibru pe direcţia forţei exterioare:

,                     (PRC-T.3.1.5.2.1.1)   

 

unde, Fs este forţa exterioară, p - presiunea pe suprafaţa de contact, As – aria suprafeţei de contact

Relaţii de calcul:

-         de verificare,

,            (PRC-T.3.1.5.2.1.2)   

 

-         de dimensionare,

 

 ,              (PRC-T.3.1.5.2.1.3)  

 

-         sarcina capabilă,

 

 ,           (RC-T.3.1.5.2.1.4)   

 

unde, σas = min(σas1, σas2) cu σas1 şi σas2  tensiunile admisibile la strivire ale materialelor corpurilor 1 şi respectiv, 2 sau σas = pa, presiunea admisibilă a peliculei de lubrifiant, pentru cazul în care corpurile sunt în mişcare relativă cu ungere

a

b

Fig. PRC-T.3.1.5.2.1.1   Modelul de calcul la strivire a suprafeţelor conforme plane: a – schema generală; b – parametri de  calcul

Obs.

a.     Tensiunile de suprafaţă (strivire), în cazul mişcărilor relative, determină, din cauza frecării, pierderi de energie şi de material (uzură) şi deci, modificări ale suprafeţelor în contact; minimizarea acestor pierderi energetice şi de material,  sunt obiective ale tribologiei (ETB-T)

 

PRC-T.3.1.5.2.2 Modelarea solicitărilor de strivire pe suprafaţele conforme cilindrice  

 

Tab. PRC-T.3.1.5.2.2.1  Calculul la strivire a suprafeţelor conforme cilindrice

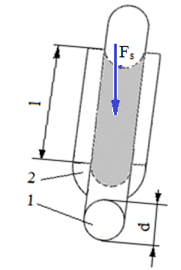
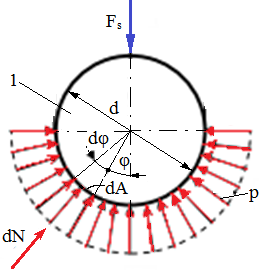
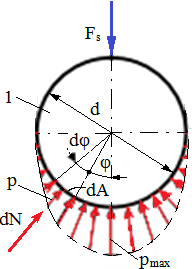
Ipoteze de calcul:

-     forţa se aplică perpendicular pe axa longitudinală a suprafeţei de contact;

-     distribuţia presiunii pe suprafaţa de contact poate fi:

-         cazul 1: bolţul este montat cu joc redus sau cu strângere şi presiunea pe suprafaţa de contact se consideră uniform distribuită pe circumferinţă şi pe generatoare;

-         cazul 2: bolţul este montat cu joc mărit şi presiunea pe suprafaţa de contact se consideră distribuită cosinusoidal pe circumferinţă după legea, p = pmax cosφ, şi uniform distribuită pe generatoare

                                 

 

 

a

b

c

Fig. PRC-T.3.1.5.2.2.1 Schema de calcul la strivire a suprafeţelor conforme cilindrice: a – parametri de calcul;  b – cazul 1, distribuţia uniformă a presiunilor de contact; c – cazul 2, distribuţia cosinusoidală a presiunilor de contact

Cazul 1. Condiţia de echilibru a forţelor:

(PRC-T.3.1.5.2.2.1)   

 

Relaţii de calcul:

-         de verificare,

,                (PRC-T.3.1.5.2.2.2)   

 

-         de dimensionare,

 ,                              (PRC-T.3.1.5.2.2.3)   

 

-         sarcina capabilă,

 ,                      (PRC-T.3.1.5.2.2.4)   

 

unde,   As = d l este aria convenţională de strivire a proiecţiei suprafeţei de contact în direcţie axială;    σas = min(σas1, σas2) cu σas1 şi σas2  tensiunile admisibile la strivire ale materialelor corpurilor 1 şi respectiv, 2 sau σas = pa [MPa], presiunea admisibilă a peliculei de lubrifiant.

Cazul 2. Condiţia de echilibru a forţelor:

=   ≈ 0,8 dl ,          (PRC-T.3.1.5.2.2.5)   

 

Relaţii de calcul:

-         de verificare,

,              (PRC-T.3.1.5.2.2.6)   

 

-         de dimensionare,

 ,                                  (PRC-T.3.1.5.2.2.7)

   

-         sarcina capabilă,

 ,                        (PRC-T.3.1.5.2.2.8)

  

unde,   As = 0,8 d l reprezintă 0,8 din aria dreptunghiului axial ca proiecţie a suprafeţei de contact în direcţie axială;   σas = min(σas1, σas2) cu σas1 şi σas2  tensiunile admisibile la strivire ale materialelor corpurilor 1 şi respectiv, 2 sau σas = pa [MPa], presiunea admisibilă a peliculei de lubrifiant.

 

 

PRC-T.3.1.6 TENSIUNI ADMISIBILE ŞI COEFICIENŢI DE SIGURANŢĂ

     

Tab. PRC-T.3.1.6.1  Condiţii de rezistenţă pentru evitarea deteriorărilor şi cedărilor

Criteriul

Relaţii

Descriere

Deteriorarea prin depăşirea limitei de curgere

 

 

;

 

 

 

σa = σ02 /c  (σa = σc /c) – tensiunea admisibilă raportată la limita de curgere pentru materiale tenace (ductile); uzual, c = 1,2…3 – coeficient de siguranţă pentru evitarea deteriorării prin deformare plastică

Deteriorarea prin depăşirea limitei de rupere

σa = σr /c – tensiunea admisibilă raportată la rezistenţa de rupere pentru materiale fragile; uzual, c = 3…4 – coeficient de siguranţă pentru evitarea cedării prin rupere

Obs.

a.     Coeficientul de siguranţă este un parametru care depinde de tipul materialului, tehnologia de obţinere a semifabricatului, mărimea şi tipul sarcinilor aplicate, regimul de funcţionare, modelul de calul (modele de calcul simple implică multe ipoteze simplificatoare şi deci coeficient de siguranţă cu valori mari), condiţiile şi mediul de lucru etc.

b.    τa = 0,8 σa, pentru o mare categorie de materiale

 

PRC-T.3.2  CALCULUL DE RIGIDITATE (DEFORMAŢII) AL ELEMENTELOR MAŞINILOR

 

Deformaţiile elastice (cu revenire la starea iniţială) şi/sau plastice (fără revenire la starea iniţială) reprezintă măsuri (valori) ale modificării (creşterii sau scăderii) distanţei dintre două puncte sau două secţiuni (deformaţii liniare), respectiv ale unghiurilor dintre două secţiuni (deformaţii unghiulare sau lunecări) ale unei structuri.

Deplasările sau săgeţile (liniare sau unghiulare) reprezintă valori ale distanţei, respectiv, unghiurilor dintre poziţiile (de obicei, iniţiale şi finale) unui punct sau ale unei secţiuni dintr-o structură; deplasările ca şi consecinţă a deformării (modificării formei) corpului pot fi: elastice (dispar după anularea sarcinii),  elasto-plastice sau plastice.

 

PRC-T.3.2.1 MODELAREA DEFORMAŢIILOR  ŞI  DEPLASĂRILOR DE VOLUM

 

Tab. PRC-T.3.1.5.1.1.1  Deformaţiile structurilor mecanice la solicitări simple

Solicitarea

Schema

Modelul matematic

Semnificaţiile parametrilor

Scop

Relaţii de calcul

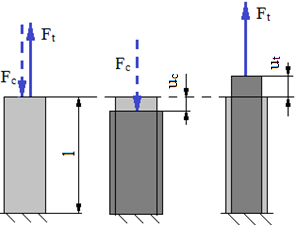
Tracţiune, compresiune

Verificare

 

Ft,c [N] –  forţa de tracţiune, compresiune;

At,c [mm2] – aria secţiunii barei solicitată la tracţiune, compresiune;

ut,c [mm] –  deplasarea (săgeta) axială;

uat,c [MPa] –  deplasarea (săgeta) axială admisibilă la tracţiune, compresiune;

Ft,c cap [N] –  forţa de tracţiune, compresiune capabilă din considerente de rigiditate;

E [MPa] – modulul de elasticitate longitudinal al materialului;

EAt,c [N] – modulul de rigiditate la tracţiune, compresiune

Dimensionare

 

Sarcina capabilă

 

 

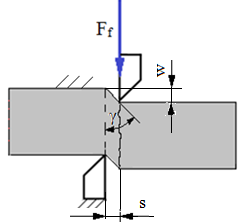
Forfecarea (tăierea) pură

Verificare

 

Ff [N] –  forţa de forfecare;

Af [mm2] –  aria secţiunii de forfecare;

w [mm] –  deplasarea (săgeta) de forfecare;

waf [mm] –  deplasarea (săgeta) de forfecare admisibilă;

γ [rad] – rotirea la forfecare;

 

Ff cap [N] –  forţa de forfecare capabilă din considerente de rigiditate;

 

G [MPa] – modulul de elasticitate transversal al materialului;

GAf [N] – modulul de rigiditate la forfecare

Dimensionare

 

Sarcina capabilă

 

 

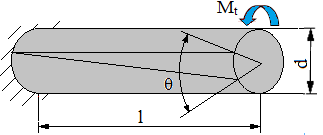
Torsiunea (răsucirea)

Verificare

 

l [mm] –  lungimea barei;

Mt [Nmm] –  momentul de torsiune (răsucire);

Ip [mm4] –  momentul de inerţie polar;

, pentru secţiune circulară;

 

θ [rad] –  deplasarea unghiulară (rotirea);

θa [rad] –  deplasarea unghiulară (rotirea) admisibilă;

G [MPa] – modulul de elasticitate transversal al materialului;

GIp  [Nmm2] – modulul de rigiditate la torsiune

Dimensionare

 

Sarcina capabilă

 

 

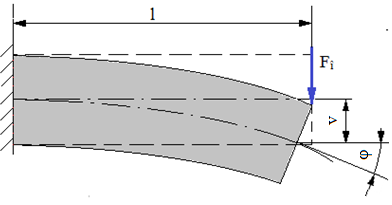
Încovoierea

Verificare

,

 

,

 

l [mm] –  lungimea barei;

v [mm] –  deplasarea (săgeta) la încovoiere;

φ [rad] –  rotirea la încovoiere;

va [mm] –  deplasarea (săgeta) la încovoiere admisibilă;

φa [rad] –  rotirea la încovoiere admisibilă;

Fî  [N] –  forţa de încovoiere;

Iz [mm4] –  momentul de inerţie axial;

–  momentul de inerţie axial al secţiunii circulare;

 [mm4] – momentul de inerţie axial necesar din condiţia deplasării, respectiv, rotirii impuse;

 

σaî  [MPa]  –  tensiunea admisibilă de încovoiere;

 

 [N] –  forţa capabilă din condiţia deplasării, respecti, rotirii impuse;

 

E [MPa] – modulul de elasticitate longitudinal al materialului;

EIz [Nmm2] – modulul de rigiditate la încovoiere

 

Dimensionare

 

 

 

 

Sarcina capabilă

 

 

 

 

Obs. Valorile deplasărilor liniare (săgeţilor) şi unghiulare (rotirilor) se determină din condiţiile de funcţionare impuse în norme şi standarde.