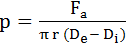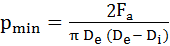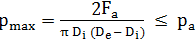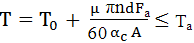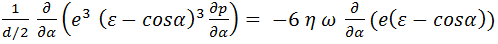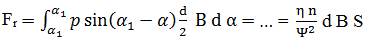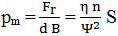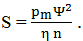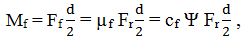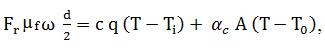LGA. LAGĂRE CU ALUNECARE

LGA-T. CONSTRUCŢIA ŞI MODELAREA LAGĂRELOR CU ALUNECARE

            CUPRINS

               LGA-T.1 DEFINIRE

                         LGA-T.2 STRUCTURI CONSTRUCTIVE

               LGA-T.3 DOMENII DE UTILIZARE, AVANTAJE ŞI DEZAVANTAJE

               LGA-T.4 CLASIFICARE

               LGA-T.5 MATERIALE ŞI TEHNOLOGII  

               LGA-T.6 FORME ŞI CAUZE DE SCOATERE DIN UZ SAU DE COMPORTARE NECORESPUNZĂTORE

               LGA-T.7 PARMETRI FUNCŢIONALI ŞI CONSTRUCTIVI            

               LGA-T.8 MODELE DE CALCUL

                               LGA-T.8.1 Modele de calcul (simplificat) a lagărelor cu frecare uscată, limită sau mixtă

                                                  LGA-T.8.1.1 Model de calcul simplificat a lagărelor radiale

                                                  LGA-T.8.1.2 Model de calcul simplificat a lagărelor axiale

                                                  LGA-T.8.1.3 Modele de calcul simplificat al lagărelor sferice

                               LGA-T.8.2 Modele de calcul a lagărelor cu frecare fluidă

                                                  LGA-T.8.2.1 Modele de calcul a lagărelor lubrifiate hidrodinamic

                                                                        LGA-T.8.2.1.1 Model de calcul a lagărelor radiale hidrodinamice

                                                                        LGA-T.8.2.1.2 Model de calcul a lagărelor axiale hidrodinamice                

                                                  LGA-T.8.2.2 Modele de calcul a lagărelor axiale lubrifiate hidrostatic

                                                                       LGA-T.8.2.2.1 Model de calcul a lagărelor radiale hidrostatice

                                                                        LGA-T.8.2.2.2 Model de calcul a lagărelor axiale hidrostatice

 

 

LGA-T.1 DEFINIRE

 

Lagărele cu alunecare sunt subansamble care materializează cuplele cinematice ce asigură rezemarea şi/sau ghidarea elementelor mobile ale maşinilor (arbori, osii)  prin intermediul unor suprafeţe de contact între care există frecare de alunecare.

 

 

LGA-T.2 STRUCTURA CONSTRUCTIVĂ

 

 

 

a

b

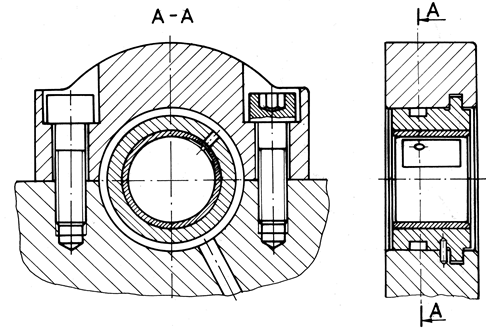
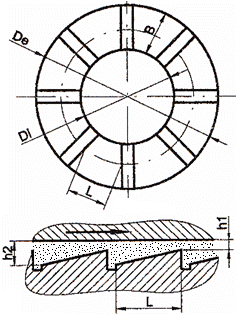
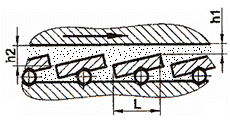
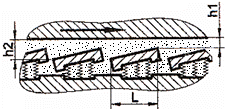
Fig. LGA-T.2.1  Structura principală a lagărelor cu alunecare [Jula,1989]: a – radial în secțiune transversală;  b – lagăre radiale în secțiune axială 

 

LGA-T.3 DOMENII DE UTILIZARE, AVANTAJE ŞI DEZAVANTAJE

 

Domenii de utilizare

Lagărele cu alunecare, comparativ cu lagărele cu rostogolire (rulmenți), sunt utilizate mai rar, în domenii și condiții specifice:

-         încărcări specifice mari (de ex. peste  2 MN) cu șocuri si vibrații importante;

-         turații foarte mari (de ex. n > 10000 rot/min) la care durabilitatea rulmenților este redusă;

-         asigurarea unor ghidări foarte precise;

-         în cazul când se impun dimensiuni de gabarit radiale foarte mari pentru care nu se execută rulmenți în serie;

-         costul unui lagăr cu alunecare este mai redus decât al unui rulment;

-         în conditii de umiditate si mediu agresiv, în care lagărele cu rostogolire nu pot fi folosite;

-         la mecanismele cu funcționare lentă (de ex. n < 10 rot/min) și puțin solicitate.

 

Tab. LGA-T.3.1 Avantajele şi dezavantajele lagărelor cu alunecare [Rădulescu, 1985]

Avantaje*

Dezavantaje*

-         viteze relative foarte mici, la care folosirea rulmenţilor poate conduce la apariţia de deformaţii locale remanente pe căile de rulare;

-         rezistenţă mare la uzare;

-         pot functiona la turaţii mari şi foarte mari, la care rulmenţii ar avea durabilităţi foarte mici;

-         funcţionare cu vibrații și zgomote reduse;

-         dimensiuni de gabarit radiale reduse și pot fi executate la dimensiuni foarte mici;

-          realizarea cuplelor cinematice care nu permit montarea axială a elementelor (arbori cotiţi)

-         Pierderi prin frecare mai mari, mai ales, la pornire

-         Gabarit în direcție axială mai mare

-          Centrare, uneori, insuficientă a elementelor care formează cupla cinematică

-         Ghidare relativ imprecisă din cauza jocului relativ mare dintre fus şi cuzinet

-         grad de standardizare mai redus

-         consum de lubrifiant mare

-         construcţii relativ complicate

-         uzarea suprafeţelor de contact ale cuplei cinematice poate conduce la înlocuirea sau remedierea unor piese complexe (arbori)

* raportate la lagărele cu rostogolire

 

LGA-T.4 CLASIFICARE

Tab. TCR-T.4.1 Clasificarea lagărelor

Criteriul

Tipul

Schema

Felul mişcării relative din cuplă

De rotaţie

Fig. LGA-T.4.1  

De translaţie (ghidaj)

Fig. LGA-T.4.2

Felul mişcării relative

Cu alunecare

Fig. LGA-T.4.1, a...d;  Fig. LGA-T.4.2,a,b,c

Cu rostogolire

Fig. LGA-T.4.1,f,g,h;  Fig. LGA-T.4.2,d,e

Hibride (cu alunecare şi rostogolire)

Fig. LGA-T.4.1,i,j;  

Tipul lubrifiantului

Cu ungere cu ulei sau unsoare consistentă

Fig. LGA-T.4.1; Fig. LGA-T.4.2

Cu ungere cu gaze

Regimul de frecare

Cu frecare limită sau mixtă

Fig. LGA-T.4.1, a...h;  Fig. LGA-T.4.2,a,b,c

Cu frecare fluidă

Fig. LGA-T.4.1;  Fig. LGA-T.4.2

Modul de realizare a frecării fluide

Hidrodinamice (HD) sau gazodinamice (GD)

Fig. LGA-T.4.1,a  

Hidrostatice (HS) sau gazostatice (GS)

Fig. LGA-T.4.1,i,j;  

Elastohidrodinamică (EHD)

Fig. LGA-T.4.1,f...i;  Fig. LGA-T.4.2,d,e

Hibride

Fig. LGA-T.4.1,i,j

Forma suprafeţei de frecare

 Cilindrice

Fig. TCR-T.4.1,a

Conice

Fig. TCR-T.4.1,c

Sferice

Fig. TCR-T.4.1,d

Plane

Fig. LGA-T.4.2,a,b,d,e

Direcţia forţei

Radiale

Fig. TCR-T.4.1,a,c...j

Axiale

Fig. TCR-T.4.1,b,e

Radial-axiale

Fig. TCR-T.4.1,c,d,f,i

Axial-radiale

Poziţia pe arbore sau osie

De capăt

Fig. LGA-T.4.1,a,c,e

Intermediare

Fig. LGA-T.4.1

Modul de rezemare

Rigidă

Fig. LGA-T.4.1

Elastică

Oscilantă

Fig. LGA-T.4.1,h

 

 

    

a

b

c

d

e

f

g

h

i

j

Fig. LGA-T.4.1  Lagăre de rotație: a – cu alunecare, radial;  b – cu alunecare, axial ;  c  – cu alunecare, conic; d  – cu alunecare, sferic; e  – cu rostogolire, axial; f  – cu rostogolire, radial-axial; g  – cu rostogolire, radial oscilant; h  – combinat cu rostogolire și frecare mixtă; i, f  – combinat cu rostogolire și alunecare hidrostatic

                                                                                                                           

a

b

c

d

e

Fig. LGA-T.4.2  Lagăre de translație (ghidaje): a – cu alunecare cu profil dreptunghiular;  b – cu alunecare cu profil triunghiular (coadă de rândunică); c – cu alunecare cu profil circular;    d – cu rostogolire cu elemente de rulare (bile sau role) nerecirculabile;  e – cu rostogolire cu elemente de rulare (bile sau role) recirculabile 

 

LGA-T.5 MATERIALE ŞI TEHNOLOGII  

 

Materiale antifricţiune pentru cuzineți

Caracteristici: rezistenţă mare la uzură; coeficient de frecare redus pentru a micşora pierderile prin frecare; să permită deformaţii plastice locale; rezistenţă mare la oboseala de contact; rezistenţă la gripare; conductibilitate termică ridicată; coeficient de dilatare termică mic; aderenţă cu lubrifiantul; rezistenţă la coroziune.

Materialele metalice feroase pentru cuzineți: fontele – cenuşii Fc, cu grafit nodular Fgn, maleabile Fma sau cele manganoase Fmn;  se obţin prin turnare; se folosesc pentru cuzineţi masivi cu ungere bogată; nu se pretează la turaţii mari şi au comportări necorespunzătoare la încărcări cu şocuri.

Materialele metalice neferoase pentru cuzineți:  bronzurile – CuSn, CuPbSn, CuPb; aliajele Cu cu Sn şi Pb se folosesc la cuzineţii multistrat obţinuţi prin turnare, iar cele ale Al – AlSn, AlPb, AlCuPb – la cuzineţi multistrat obţinuţi prin placare; se utilizează în construcţia cuzineîilor masivi pentru sarcini şi turaţii ridicate.

Materialele nemetalice pentru cuzineți: textolitul – sub formă de cuzineţi masivi este rezistent la coroziune (ungere cu apă) şi amortizează şocurile; lemn – stejar – presat şi impregnat; materiale plastice – bachelite (termorigide), pentru cuzineţi masivi şi teflon sau poliamide – cu proprietăţi autolubrifiante; cauciuc – cuzinet multistrat vulcanizat (ungere cu apă); grafit; ceramică – cuzineţi masivi din ceramică fină; pietre preţioase – în mecanica fină;

Materialele sinterizate pot fi: moi, pe bază de FeC, FeCu, CuPb, AlCuPb, utilizate la cuzineţi masivi, poroşi şi autolubrifianţi executaţi multistrat subţiri; dure, pe bază de carburi metalice, utilizate la lagăre cu gaze.

Materiale mixte: suport metalic din bandă de oţel şi strat sinterizat (bronz) şi lubrifiant solid.

 

Materiale antifricţiune pentru fusuri (patine)

În majoritatea cazurilor, fusurile (patinele) se execută din acelaşi material ca şi osia sau arborele de care aparţin, cu precădere din oţeluri carbon de cementare sau de îmbunătăţire. La condiţiile impuse materialelor arborilor şi osiilor se mai adaugă: rezistenţă mare la uzare; prelucrare corespunzătoare a suprafeţei.

Se recomandă ca duritatea fusului să fie de 3…5 ori mai mare decât a cuzinetului, acest raport asigurând o funcţionare corespunzătoare şi când ungerea este defectuoasă. Pentru materialele de cuzineţi cu duritate < 300 HB nu mai este necesară durificarea fusului. Fusurile nedurificate mai importante se vibronetezesc, iar fusurile durificate prin călire sau cementare şi călire trebuie rectificate.

 

 

LGA-T.6 FORME ŞI CAUZE DE SCOATERE DIN UZ SAU DE COMPORTARE NECORESPUNZĂTOARE

 

Tab. LGA-T.6.1 Forme şi cauze de comportare necorespunzătoare sau de scoatere din uz

Forme

Consecinţe

Apariţie

Cauze

Manifestare

Evitare

Deteriorarea suprafeţelor active

Comportare necorespunzătoare

Cu precădere, în cazul lagărelor cu ungere semiuscată

Uzarea

Mişcări neuniforme cu vibraţii și zgomote

Limitarea uzurilor

Gripare

Scoaterea din uz

Cu precădere, în cazul lagărelor cu ungere necorespunzătoare la sarcini şi turaţii mari

Uzură catastrofală

Întreruperea mişcării relative (blocare)

Limitarea temperaturilor şi a tensiunilor maxime statice sau de oboseală la valori admisibile;

Asigurarea unei ungeri corespunzătoare

 

LGA-T.7 PARAMETRI FUNCŢIONALI ŞI CONSTRUCTIVI

 

Tab. LGA-T.7.1 Forme  şi parametri funcţionali ai cuzineţilor

Forma

Tipul

Parametri

Descriere, utilizări

 

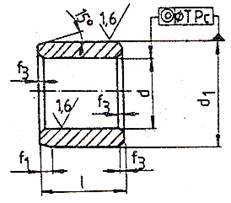
Bucşă

Monobloc cu pereți groși

d, l, d1

Se utilizează în construcția lagărelor radiale nedemontabile, de obicei, la cap de arbore;

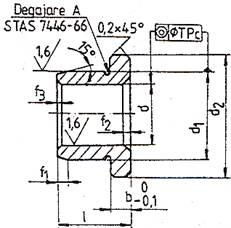
Monobloc cu pereți groși şi guler

 d, l, d1, b

Tehnologii de realizare simple – prelucrări prin așchiere a unui semifabricat turnat sau laminat; deformabilități reduse

Înfășurată cu pereți subțiri

 

 

Semibucşă

 

 

 

 

a

b

c

d

e

 

f

g

h

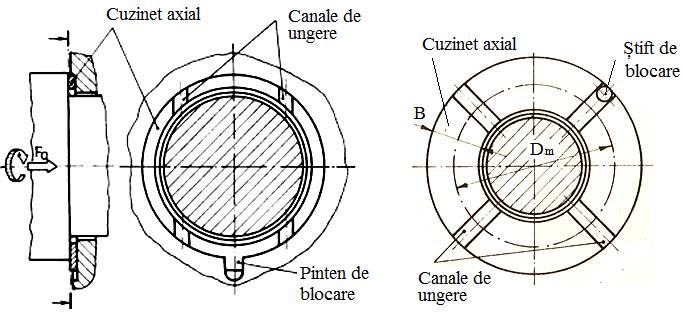
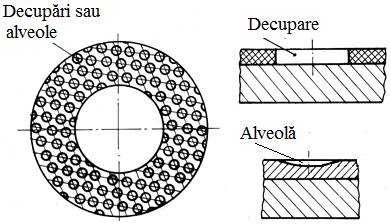
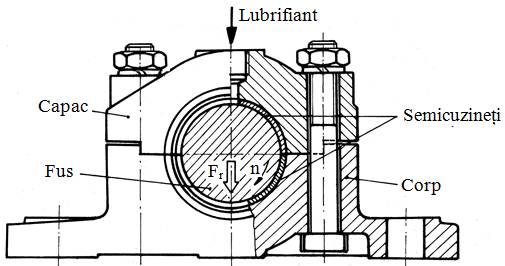
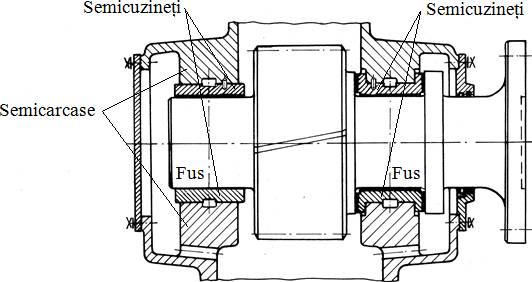
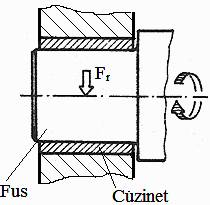
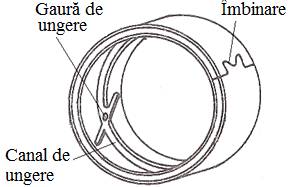
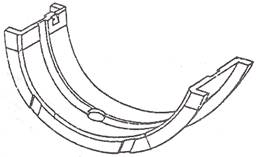
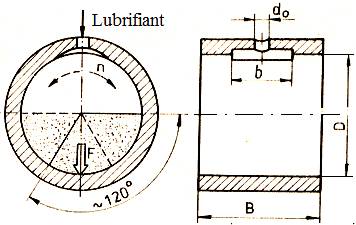
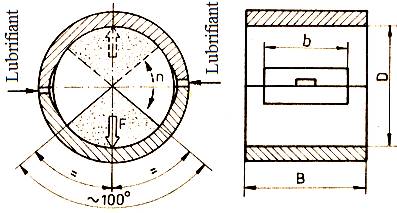
Fig. LGA-T.7.1  Forme de cuzineţi: a – bucşă; b – bucşă cu guler; c – bucşă înfăşurată subţire; d – semicuzinet; e – semicuzineţi ([http://ro.wikipedia.org/wiki/cuzinet]; f – bucşă cu alveolă de ungere; g – semicuzineţi cu alveole de ungere; b – bucşă cu canal inelar de ungere

 

LGA-T.8 MODELE DE CALCUL

                                                                              

LGA-T.8.1 Modele de calcul (simplificat) a lagărelor cu frecare uscată, limită sau mixtă 

 

LGA-T.8.1.1 Model de calcul simplificat a lagărelor radiale

 

Pentru un volum de material Vu  acceptat şi o durabilitate Lh impusă, ţinând cont de relaţia (LGA-T.8.1.2) se determină relaţia de verificare,

 

pvm  ≤ (pv)au                                              (LGA-T.8.1.3)

 

în care,  (pv)au [MPa.m/s] este produsul presiune-viteză admisibil din considerente de uzare impusă într-o perioadă de timp Lh, are valori dependente de de materialele în contact (anexa LGA-P.1.1).

Calculul termic

Modelul 1 (verificare sumară)

Încălzirea lagărului este determinată de puterea specifică (pe unitatea de suprafaţă de contact) pierdută prin frecare,

         (LGA-T.8.1.4)

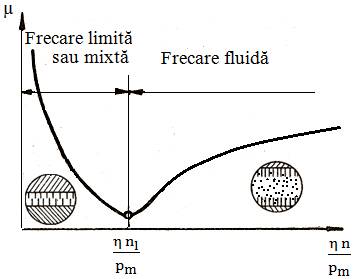
Considerând   coeficientul de frecare µ constant produsul pmv  din relaţia de mai sus este un indicator al nivelului de încălzire şi pentru verificare,

pmv ≤ (pv)aî,

unde  (pv)aî produsul presiune-viteză admisibil din considerente de încălzire admisă are valori obţinute experimental pentru diferite materiale şi domenii de utilizare.

Modelul 2 (determinarea temperaturii medii a lagărului (uleiului))

Ecuația bilanțului termic,

Pf = Qc,     

în care, Pf este puterea pierdută prin frecare și Qc căldura evacuată prin corpul lagărului mediului exterior, în formă explicită devine,

          (LGA-T.8.1.5)

 

unde, µ este coeficientul de frecare, T – temperatura medie a lagărului inclusiv a lubrifiantului; T0 – temperatura mediului ambiant, αc - factorul global de transfer a căldurii prin carcasa lagărului, A – aria suprafeței exteriore a carcasei; ω = πn/30, viteza unghiulară a fusului (turația, n [rot/min]). Din această relație se determină temperatura medie,

 .        (LGA-T.8.1.6)

unde Ta este temperatura admisibilă.

Calculul fusului la încovoiere

În cazul B/D > 1 pot apărea tensiuni de încovoiere maxime în zona concentratorului determinat de saltul de diametre,

.          (LGA-T.8.1.7)

 Obs. În cazul arborilor cu flexibilitate mărită în relaţia (LGA-T.8.1.7) se consideră braţul forţei l egal cu lungimea fusului, B.

a

b

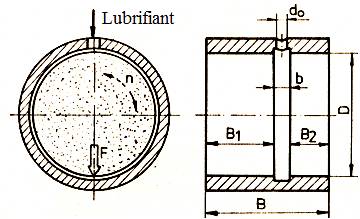
Fig. LGA-T.8.1.1.1  Model de calcul simplificat a lagărului radial : a –schema de calcul ; b – secţiune axială cu abateri de coaxialitate

Ipoteze:

-         fusul se consideră ca o grindă dreaptă încastrată în tronsonul adiacent al arborelui;

-         suprafețele de contact se consideră netede și nedeformabile;

-         presiunea de contact, pm, se consideră uniform distribuită (nu se ține seama de jocuri, erori de prelucrare și montaj și de uzuri);

-          coeficientul de frecare se consideră constant;

-          se neglijează teşiturile şi racordarea;

-         fusul şi cuzinetul se consideră coaxiale.

Calculul presiunii medii de contact

Din ecuația de echilibru a forțelor în direcția forței radiale,

   =

 

rezultă relația de verificare la presiunea de contact,

,   (LGA-T.8.1.1)

 

unde presiunea admisibilă, pa, se adoptă în funcție de materialele în contact (anexa LGA-P.1.1) sau din condiţia de neexpulzare a lubrifiantului; pentru proiectarea cuzineților nestandard se adoptă B/D < 1,2 (pentru valori mai mari crește neuniformitatea distribuției presiunii de contact în direcție axială, fig.  LGA-T.8.1,b)

Calculul de uzare (durabilitate)

Volumul de material rezultat prin uzare ,

        (LGA-T.8.1.2)

 

în care,  l = v Lh este lungimea parcursă de un punct exterior al fusului, k – factor de proporţionalitate dependent de cuplul de materiale şi de condiţiile de ungere; Lh - durata de funcţionare, v – viteza periferică.

 

LGA-T.8.1.2 Model de calcul simplificat a lagărelor axiale

 

a

 

b

 

c

 

Ipoteze:

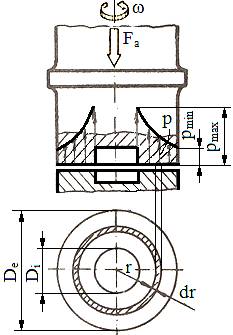
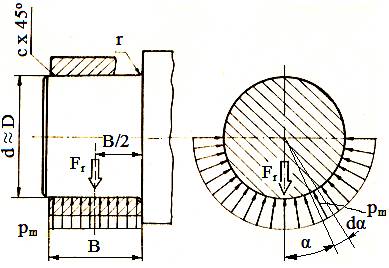
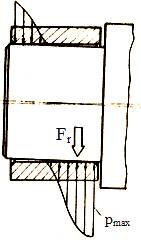
-         dependența hiperbolică a presiunii de contact în raport cu raza conduce la presiuni mărite (teoretic ) în centrul pivoților cu secțiune circulară (fig. LGA-T.8.1.2.1,a); pentru evitarea acestui dezavantaj în cazurile practice se folosesc pivoți cu secțiune inelară (fig. LGA-T.8.1.2.1,b);

-          pentru perioada de exploatare se poate considera uzarea neuniformă a suprafețelor în contact, pv = p ω r  = ct. (p r = ct.);

-          pentru perioada de funcţionare incipientă (rodaj) se poate considera distribuţia presiunii constantă p = ct. (fig. LGA-T.8.1.2.1,b).

 

Calculul presiunilor în ipoteza presiunii neuniforme (fig. LGA-T.8.1.2.1,b)

Din echilibrul forțelor în direcție axială,

 

 

 

 rezultă relația presiunii

,  (LGA-T.8.1.7)

 

din care, pentru r=De/2 şi r=Di/2 se obţine,

 

  şi respectiv,    

 

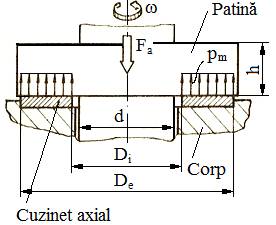
Calculul presiunilor în ipoteza presiunii uniforme (fig. LGA-T.8.1.2.1,c)

   (LGA-T.8.1.8)

 

 

Calculul termic

 

pmv ≤ (pv)aî,

Temperatura medie a lagărului se determină similar ca în cazul lagărului radial (LGA-T.8.1.6),

        (LGA-T.8.1.9)

 

unde, d = Dm = (De – Di)/2 este diametrul mediu.

 

Calculul de uzare (durabilitate)

 

pvm  ≤ (p v)au               (LGA-T.8.1.10)

 

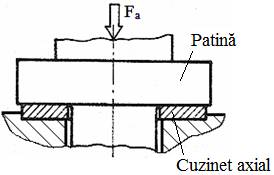
Fig. LGA-T.8.1.2.1  Modele de calcul simplificat ale lagărelor axiale: a – lagăr cu suprafaţă de contact circulară şi presiune neuniformă; b – lagăr cu suprafaţă de contact inelară şi presiune neuniformă; c – lagăr cu suprafaţă de contact inelară şi presiune uniformă

          

                                                                           a                                                                                                                                 b                                          c

                                          Fig. LGA-T.8.1.2.2  Soluţii constructive de lagăre axiale:  a - cu canale de ungere transversale; b - cu canale de ungere radiale; c - cu alveole

 

LGA-T.8.1.3 Modele de calcul simplificat al lagărelor sferice

 

  

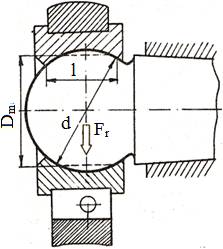
Calculul presiunii pentru articulaţii standard (fig. LGA-T.8.1.3.1)

Ipoteze:

-         fusul sferic se consideră cilindric cu diametrul mediu Dm =  0,9 d;

-         se consideră încărcat numai cu forța radială.

Presiunea medie

    (LGA-T.8.1.11)

 φ = l/Dm  0,7

Calculul de durabilitate pentru articulaţii standard

Relația de verificare,

P  C,                  (LGA-T.8.1.12)

 

unde, P este sarcina dinamică echivalentă P = Fr + YFa cu Y este 6 pentru sarcini statice și 12 pentru sarcini dinamice și C capacitatea de încărcare dinamică (de catalog), ca fiind sarcina radială care o poate prelua fusul sferic fără să se deterioreze prin gripare când oscilează cu  30o, 5000 de cicluri la presiunea de contact 250MPa (C5000) sau 10000 de cicluri la presiunea de contact 20 MPa (C5000).

a

b

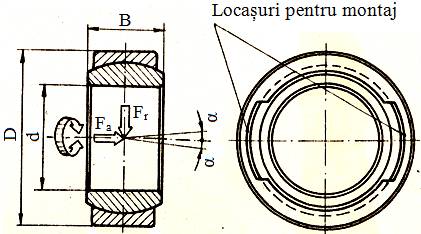
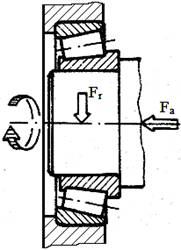
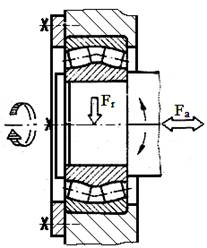
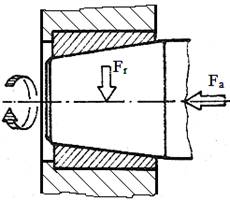
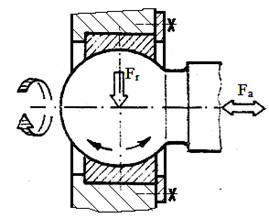
Fig. LGA-T.8.1.3.1  Modele de calcul simplificat ale lagărelor (articulaţiilor) sferice: a – cu structura nonstandard; b – cu structura standard

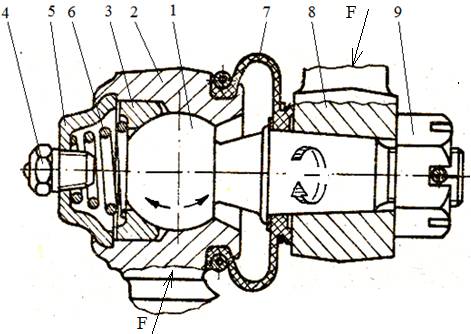
Fig. LGA-T.8.1.3.2  Articulaţie sferică din componenţa mecanismelor de direcţie-suspensie ale autovehiculelor

Construcţie  şi funcţionare : 

Forţa se transmite de la braţul 8 prin frecare, în asamblarea presată pe con, la fusul sferic 1 şi,  în continuare, prin formă, de lagărul sferic compus din două semisfere practicate în corpul 2 şi în semicuzinetul 3 la celălalt braţ solidar cu corpul 2. Asamblarea presată pe con este strânsă cu piuliţa crenelată 9 care este asigurată cu şplint (cui spintecat). Contactul permanent în articulaţia sferică este realizat prin intermediul arcului elicoidal conic 6 sprijinit pe şaiba de reazem 5. Ungerea articulaţiei sferice se face cu unsoare consistentă prin intermediul ungătorului  cu bilă 4. Etanşarea articulaţiei se face cu burduful 7.

 

LGA-T.8.2 Modele de calcul a lagărelor cu frecare fluidă

 

LGA-T.8.2.1 Modele de calcul a lagărelor lubrifiate hidrodinamic

 

LGA-T.8.2.1.1 Model de calcul a lagărelor radiale hidrodinamice

 

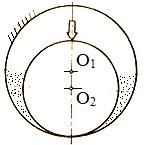
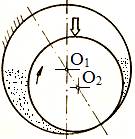
Procesul formării filmului de lubrifiant portant:

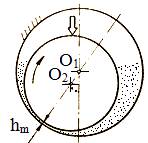
a.     fusul este în stare de repaus, între suprafețe apare contact direct metal-metal în zona inferioară (fig. LGA-T.8.2.1,a);

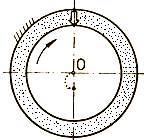
b.    Demaraj fus, contact direct și frecare uscată sau semiuscată la turație redusă (fig. LGA-T.8.2.1,b);

c.      Turaţia creşte şi începând cu o valoare limită se dezvoltă filmul de lubrifiant, ca urmare a existenței condițiilor efectului de pană, lubrifiantul este antrenat în sensul mișcării (fig. LGA-T.8.2.1,c) și se trece treptat de la frecarea uscată la frecarea mixtă și în final la cea fluidă (fig. LGA-T.8.2.2,b);

d.    Turaţii extrem de mari şi se continuă modificarea poziției relative a suprafețelor în contact (crește grosimea filmului de lubrifiant), teoretic, la n ŕ  fusul și cuzinetul ajung concentrice.

a

b

c

d

Fig. LGA-T.8.2.1  Procesul formării filmului de lubrifiant: a – repaus; b  –  pornire şi turaţie redusă; c – dezvoltare film de lubrifiant; d – turaţii foarte mari (caz teoretic)

 

 

Ipoteze de calcul:

-         există condițiile lubrifierii hidrodinamice: forma geometrică de pană datorită jocului fus-cuzinet; există lubrifiant în zona de contact şi există viteză de rotație relativă fus-cuzinet;

-         se consideră fusul de lungime foarte mare (curgerea fluidului unidirecțională);

-         se neglijează efectele forțelor centrifuge

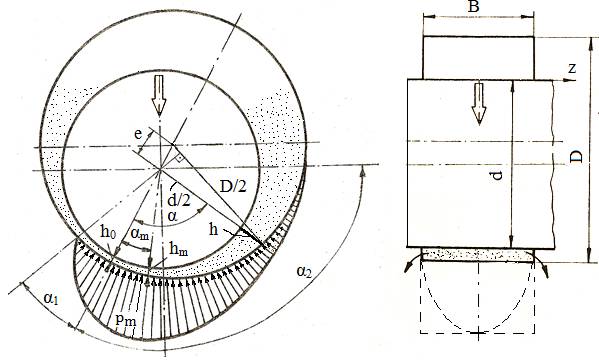
Parametrii de calcul: d – diametrul fusului;  D – diametrul cuzinetului; B – lățimea cuzinetului; h – grosimea filmului de lubrifiant într-o secțiune oarecare; e – excentricitatea; j = (D-d)/2, jocul diametral; Ψ = (D-d)/d = j/d, jocul relativ;  ɛ = e/(j/2), excentricitatea relativă; δ = h0/(j/2), grosimea minimă relativă (δ + ɛ  = 1); h0, h, hm – grosimile filmului de lubrifiant (minimă, curentă și, respectiv, corespunzătoare presiunii maxime, pm); α, α1, α2, αm – unghiul curent, de intrare, de ieșire și respectiv corespunzător presiunii maxime;  Fr  - forța radială

   

a

b

Fig. LGA-T.8.2.2  Modelul de calcul a lagărelor radiale hidrodinamice: a – schema de calcul;  b – curba Stribeck asociată

Modelul de calcul a parametrilor ungerii hidrodinamice

Particularizarea ecuației lui Reynolds (v. rel. ETB-T.4.3.1.1) pentru lagărele radiale hidrodinamice  considerând x = d/2 α, dx = d/2 dα, v=ω d/2  și variația grosimii peliculei de lubrifiant (fig. LGA-T.8.2.2,a),

 

 

devine,

 

    (LGA-T.8.2.1)

 

Prin integrarea acestei ecuației de două ori în funcție de variabila unghiulară α se obține variația presiunii în interiorul filmului de lubrifiant,  p = p(α, d/2, ω, ɛ, η).

Portanța filmului de lubrifiant  se obține prin integrare ca sumă a presiunilor distribuite pe suprafața de contact,

 

          (LGA-T.8.2.2)

 

unde S0 este numărul lui Sommerfeld sau cifra de portanță, mărimea adimensională. În proiectare se folosește frecvent coeficientul de portanță, Cp = 1/S0.

Ţinând cont de relația (LGA-T.8.2.2) rezultă presiunea medie convențională,

 

.                          (LGA-T.8.2.3)

 

În cazul cunoașterii presiunii medii (prin determinări experimentale) din relația (LGA-T.8.2.3) se determină,

 

                                     (LGA-T.8.2.4)

 

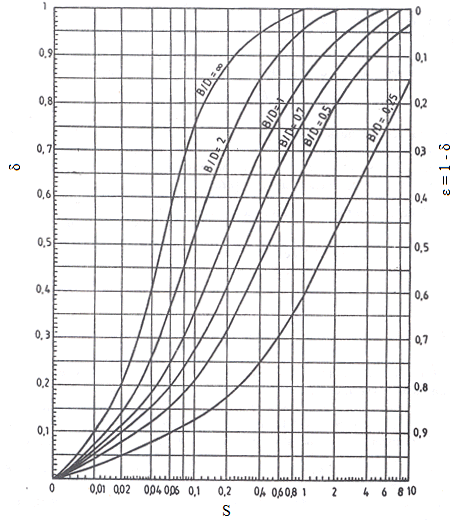
în care η este vâscozitatea dinamică, n – turația în rot/min.

În Fig. LGA-T.8.2.3 se prezintă dependenţa numărului lui Sommerfeld în funcţie de grosimea minimă relativă, δ = h0/(j/2),  excentricitatea relativă, ɛ = e/(j/2) şi raportul B/d. Pentru proiectare cunoscâd valoarea numărului lui Sommerfeld se poate determina grosimea minimă a peliculei de lubrifiant, h0 care trebuie să fie mai mare decât suma rugozităţilor fusului şi cuzinetului.

Momentul de frecare

                 (LGA-T.8.2.6)

unde, cf = µa/Ψ = 2 π2 S este coeficientul pierderilor prin frecare [Olaru, 2002]; coeficientul de frecare de alunecare, µf  = cf Ψ =  2 π2 S Ψ = 2 π2 η n pm Ψ.

Modelul de calcul termic al lagărului uns hidrodinamic

Ecuația echilibrului termic,

 

Pf = W1  + W2                                   (LGA-T.8.2.7)

 

exprimă egalitatea puterii pierdută prin frecare, Pf, cu suma căldurilor W1 și  W2 evacuate și transferate lubrifiantului (aflat în circulație) și, respectiv, de mediului înconjurător (atmosferă).

Relația (LGA-T.8.2.6) în urma explicitării devine,

 

     (LGA-T.8.2.8)

 

unde, c este căldura specifică a lubrifiantului, q – debitul lubrifiantului,  T – temperatura medie a lagărului inclusiv a lubrifiantului, Ti – temperatura uleiului la intrare (T= Ti +5…8 0C), T0 – temperatura mediului ambiant, αc - factorul global de transfer a căldurii prin carcasa lagărului, A – aria suprafeței exteriore a carcasei; ω = πn/30, viteza unghiulară a fusului (turația, n [rot/min]). Pentru proiectare din relația (LGA-T.8.2.8) se determină temperatura de funcționare T care se impune să fie mai mică decât temperatura admisibilă de funcționare a uleiului Ta = 60...80 0C

Obs.

a.     Jocul radial influențează funcționarea, frecarea și încălzirea lagărului; jocul se modifică cu diferența temperaturilor de lucru și de montaj; valoarea jocului se modifică în timpul funcționării, mai ales, accelerat în perioada rodajului; la jocuri mari pot apărea deformații unghiulare mărite ale fusurilor; jocul relativ, Ψ = (0,3...3) o/oo pentru lagăre cu cuzineți metalici; ajustajele recomandate pentru subansamblul fus-cuzinet  pot fi: H7/g6 sau H7/f7, pentru fusuri încărcate la presiuni mari care lucrează la turații joase; H7/d8 sau H7/e8 pentru fusurile care lucrează la turații mari

b.    Grosimea minimă a peliculei de lubrifiant, h0, trebuie să fie mare decât limita inferioară admisibilă determinată de condițiile de execuție (rugozități) a suprafețelor și de deformarea elastică a fusului; pentru lagăre normale îngrijit prelucrate condiția de existență a frecării fluide poate fi exprimată prin condiția, h0 > 10 µm; grosimea minimă admisibilă a filmului de lubrifiant, mai ales, în cazul ungerii prin circuit exterior, trebuie să fie mai mare cu nivelul de filtrare 10…15 µm.

c.      Din punct de vedere al ungerii și al răcirii lagărele hidrodinamice pot fi cu sistem de ungere propriu și răcire prin corpul lagărului sau cu ungere prin circuit exterior și răcire prin lubrifiant.

 

    

Fig. LGA-T.8.2.3  Variaţia grosimii minime relative, δ = h0/(j/2), în funcţie de  numărul lui Sommerfeld, S = η n/pmΨ2 şi de raportul B/d [Olaru, 2002]

 

 

 

 

 

Fig. LGA-T.8.2.4  Lagăr radial hidrodinamic cu un cuzinet monobloc alimentat printr-o alveolă

 

LGA-T.8.2.1.2 Model de calcul a lagărelor axiale hidrodinamice

 

 

 

 

Forme constructive

Pentru obținerea realizarea peliculei de autoportante de lubrifiant (obținerea efectului de pană hidrodinamică ) se sectorizează suprafața inelară a cuzinetului cu sectoare fixe (pentru un singur sens de rotație), articulate (oscilante) sau rezemate elastic 

Elemente de calcul

Calculul se face echivalând sectorul real cu unul dreptunghiular de lăţime B şi  lungime L = (πDm/z-l), considrerând în locul mișcării de rotație o mișcare de translație cu viteza v= π Dm n/30 unde n [rot/min] este turația,  şi Dm = (De – Di)/2 diametrul mediu.

b

a

c

Fig. LGA-T.8.2.3  Formele zonelor de active ale lagărelor axiale hidrodinamice: a – cu sectoare fixe; b – cu sectoare mobile articulate; b – cu sectoare mobile rezemate elastic

 

 

LGA-T.8.2.2 Modele de calcul a lagărelor axiale lubrifiate hidrostatic

 

LGA-T.8.2.2.1 Model de calcul a lagărelor radiale hidrostatice

 

 

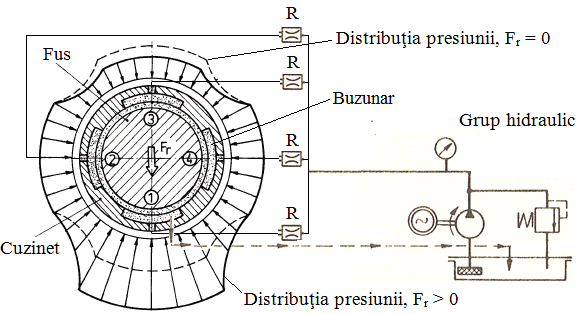
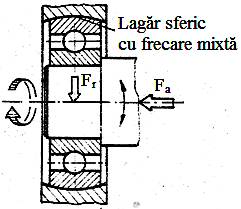
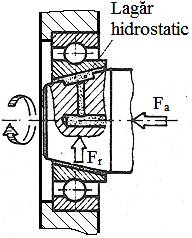
Fig. LGA-T.8.2.5   Schema funcţională a lagărelor radiale hidrostatice

Particularităţi funcţionale şi constructive:

-       Se folosesc la încărcări mari şi viteze reduse (când nu se poate realza filmul autoportant hodrodinamic) şi/sau în cazul preciziilor mărite (când lagărele hidrodinamice cu joc impus sunt necorespunzătoare); au frecări reduse şi la pornire

-       Ca urmare a introducerii de către grupul hidraulic (instalaţie de alimentare) prin restrictorii hidraulici, R a lubrifiantul (uleiul) sub presiune, în buzunarele (degajările) practicate în cuzinet se dezvoltă un film de lubrifiant portant chiar şi în cazul inexistenţei mişcării de rotaţie.

-       Pentru preluarea sarcinilor radiale se pot folosi lagăre radiale parţiale (deschise), care pot funcţiona stabil cu un singur buzunar (forţa radială unidirecţională) sau lagăre radiale complete care nu pot funcţiona stabil decât cu minim trei buzunare (uzual au 4, sau 6 buzunare, fig.  LGA-T.8.2.2).

Particularităţi de calcul:

Se calculează similar ca în cayul lagărelor hidrodinamice:

-         forţa portantă,

-         debitul de lubrifiant,

-         puterile consumate prin frecare şi pompare

 

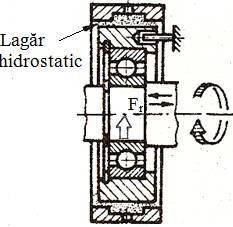
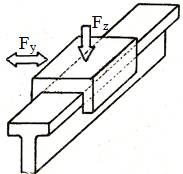
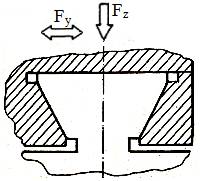
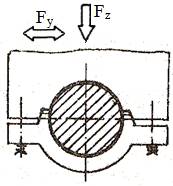
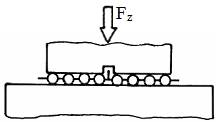
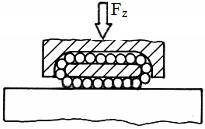
LGA-T.8.2.2.2 Model de calcul a lagărelor axiale hidrostatice
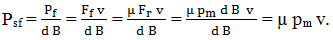
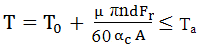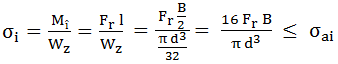