a
b
c
d
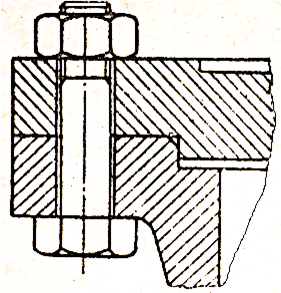
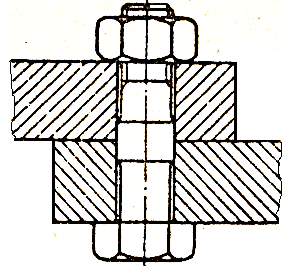
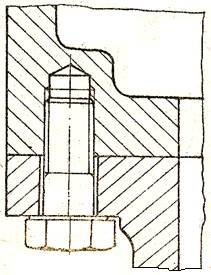
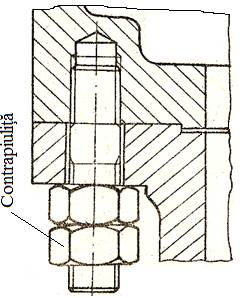
Fig. AFS-T.2.1 Asamblări cu şurub: a – cu joc în găuri de trecere; b – fără joc în găuri de trecere; c – cu joc în gaură filetată înfundată; d –de tip prezon cu piuliţă şi contrapiuliţă
|
CUPRINS |
|
AFS-T.1 DEFINIRE AFS-T.2 STRUCTURI CONSTRUCTIVE AFS -T.3 DOMENII DE UTILIZARE, AVANTAJE ŞI DEZAVANTAJE AFS -T.4 CLASIFICARE AFS -T.5 MATERIALE ŞI TEHNOLOGII AFS -T.6 FORME ŞI CAUZE DE SCOATERE DIN UZ SAU DE COMPORTARE NECORESPUNZĂTORE AFS -T.7 PARMETRII FUNCŢIONALI ŞI CONSTRUCTIVI AFS -T.8 MODELE DE CALCUL AFS-T.8.1 Modele de calcul a forţelor şi momentelor din asamblările filetate AFS-T.8.1.1 Modele de calcul a forţelor şi momentelor din asamblările filetate nepretensionate AFS-T.8.1.2 Modele de calcul a forţelor din asamblările filetate pretensionate AFS-T.8.2 Model de calcul de rezistenţă a asamblării filetate AFS-T.8.3 Modele de calcul de rezistenţă a asamblărilor cu şuruburi AFS-T.8.3.1 Modele de calcul de rezistenţă al asamblărilor cu şuruburi solicitate axial AFS-T.8.3.2 Modele de calcul de rezistenţă al asamblărilor cu şuruburi solicitate transversal AFS -T.9 STRUCTURI CONSTRUCTIVE AFS -T.9.1 Formele constructive ale şuruburilor, piuliţelor şi şaibelor plate AFS -T.9.2 Soluţii pentru optimizarea constructivă a asamblărilor filetate şi cu şuruburi AFS -T.9.3 Asigurarea asamblărilor filetate împotriva autodesfacerii |
AFS-T.1 DEFINIRE
Filetul se prezintă sub forma unor spire (proeminenţe) elicoidale dispuse uniform pe o suprafaţă cilindrică, conică sau de alt tip la exterior sau la interior.
Asamblările filetate sunt legăturile directe demontabile realizate prin contactul direct dintre filetele conjugate, interior (al piuliţei) şi exterior (al şurubului).
Asamblările prin şuruburi sunt asamblări demontabile care poziţionează şi fixează două sau mai multe elemente (piese) prin intermediul uneia sau mai multor asamblări filetate (şurub-piuliţă).
AFS-T.2 STRUCTURI CONSTRUCTIVE
|
|
|
|
|
|
a |
b |
c |
d |
|
Fig. AFS-T.2.1 Asamblări cu şurub: a – cu joc în găuri de trecere; b – fără joc în găuri de trecere; c – cu joc în gaură filetată înfundată; d –de tip prezon cu piuliţă şi contrapiuliţă |
|||
AFT-T.3 DOMENII DE UTILIZARE, AVANTJE ŞI DEZAVANTAJE
Domenii principale de utilizare: construcţia de maşini, utilaje, instalaţii tehnologice, construcţii etc.
Tab. AFS-T.3.1 Avantajele şi dezavantajele asamblărilor filetate
|
Avantaje* |
Dezavantaje* |
|
- forţe de strângere (fixare) mari; - uşor de montat şi de demontat cu forţe reduse; - sigure în exploatare; - ieftine deoarece se execută în întreprinderi specializate, în producţie de masă; - sunt interschimbabile, la scară internaţională; - asigură condiţia de autofixare, cu precădere, în condiţii de încărcare statice |
- filetul, prin forma sa este un puternic concentrator de tensiuni; - necesită asigurare suplimentară împotriva autodesfacerii, mai ales în cazul solicitărilor dinamice (vibraţii) |
AFS-T.4 CLASIFICARE
Tab. AFS-T.4.1 Clasificarea filetelor
|
Criteriul |
Tipul |
Schema |
Descriere |
|
Destinaţia |
De fixare |
Se utilizează în construcţia asamblărilor filetate |
|
|
De măsurare/reglare |
Sunt utilizate în construcţia aparatelor de măsură (micrometre)/sunt utilizate pentru poziţionarea relativă a unor elemente din construcţia sistemelor mecanice |
||
|
De mişcare |
Se utilizează în construcţia cuplelor elicoidale (transmisii şurub-piuliţă) |
||
|
Numărul începuturi |
Cu un început |
Fig. AFT-T.2.2,a |
|
|
Cu două sau mai multe începuturi |
Fig. AFT-T.2.2,c |
Se utilizează pentru deplasări (curse) mari corespunzătoare unor unghiuri de rotire mici; apare pericolul nerespectării condiţiei de autofrânare |
|
|
Sensul de înfăşurare al spirei filetului |
Pe dreapta |
Fig. AFT-T.2.2,c |
Viteza unghiulară, ω are acelaşi sens cu viteza liniare, v. |
|
Pe stânga |
Viteza unghiulară, ω are sens opus vitezei liniare, v. |
||
|
De sistemul de măsurare |
Metrice |
Au dimensiunile în mm şi sunt standardizate; unghiul profilului, α = 60o |
|
|
În ţoli |
Au dimensiunile în ţoli şi sunt folosite rar; unghiul profilului, α = 55o. |
||
|
Suprafaţa pe care se genereză filetul |
Cilindrice (exterioare, interioare) |
|
|
|
Conice (exterioare, interioare) |
|
|
|
|
Mărimea pasului filetului |
Cu pas mare |
|
Apare pericolul nerespectării condiţiei de autofrânare |
|
Cu pas normal |
|
|
|
|
Cu pas fin |
|
Se folosesc pentru filetele de măsurare şi de reglare; îndeplinesc foarte bine condiţia de autofrânare |
|
|
Forma profilului spirei |
Triunghiular cu unghiul, α = 60o |
|
Asamblări de fixare |
|
Triunghiular cu unghiul, α = 55o |
|
Asamblări de fixare şi de etanşare |
|
| Pătrat, α = 0o | Pentru cuple elicoidale cu randament mai mare, dar imprecise | ||
| Trapezoidal, α = 30o | Pentru cuple elicoidale cu randament mai redus, dar mai precise |
|
|
|
|
|
|
a |
b |
c |
d |
|
Fig. AFS-T.4.1 Particularităţi de generare a filetului: a – vedere de ansamblu a procesului de generare ; b – variaţia unghiului de înclinare a spirei filetului cu diametrul; c – direcţia elicei (dreapta, stânga); d – filete multielice (cu două începuturi) |
|||
AFS-T.5 MATERIALE ŞI TEHNOLOGII
Oţelurile (S235, E285, C35, C45, 40Cr10, 33MoCr11, 13CrNi30 etc.) pentru şuruburi şi piuliţe de fixare standardizate sunt împărţite în grupe de caracteristici mecanice, fiecare grupă fiind asociată unor materiale cu caracteristici apropriate. Simbolurile grupelor de caracteristici mecanice uzuale pentru şuruburi sunt: 3.6, 4.6, 4.8, 5.6, 5.8, 6.8, 8.8, 10.9, 12.9; semnificaţie: primul număr x 100 = rezistenţa la rupere minimă (σrmin) în MPa şi primul număr x numărul al doilea x 10 = rezistenţa la curgere minimă (σcmin) în MPa (ex. pentru grupa 6.8, σrmin = 6 x 100 = 600 MPa, σcmin = 6 x 8 x 10 = 480 MPa). Simbolurile grupelor de caracteristici mecanice uzuale pentru piuliţe sunt: 4, 5, 6, 8, 10, 12; semnificaţie: numărul x 100 = rezistenţa la rupere minimă (σrmin) în MPa (ex. pentru grupa 8, σrmin = 8 x 100 = 800 MPa).
Tehnologia de execuţie a filetelor se face în funcţie de seria de fabricaţie: în cazul unicatelor şi seriilor mici se face prin filetarea cu filiera, pentru şurub, şi cu tarodul, pentru piuliţă, sau prin strunjire cu cuţite de filetat (se intrerupe fibrajul, fig. AFS-T.5.2, a) în cazul seriilor de fabricaţie mari filetarea se face, prin aşchiere cu scule speciale (cuţit pieptene sau disc) sau prin deformare plastică prin rulare (se păstrează continuitatea fibrelor materialului, fig. AFS-T.5.2, b), pe maşini automate.
|
|
|
|
|
a |
b |
|
|
Fig. AFS-T.5.1 Marcarea grupei carateristicilor de material |
Fig. AFS-T.5.2 Forma fibrei semifabricatului laminat în zona filetului: a – prelucrat prin aşchiere (strunjire); b – deformare plastică la rece |
|
AFS-T.6 FORME ŞI CAUZE DE SCOATERE DIN UZ SAU DE COMPORTARE NECORESPUNZĂTOARE A ASAMBLĂRILOR FILETATE
Tab. AFS-T.6.1 Forme şi cauze de comportare necorespunzătoare sau de scoatere din uz
|
Forme |
Consecinţe |
Apariţie |
Cauze |
Manifestare |
Evitare |
|
Rupera tijei şurubului la suprasarcini |
Scoaterea din uz |
Ruperea apare în zona secţiunii cu aria minimă (fig. AFS-T.6.2,a,b) |
Suprasarcnii accidentale şi/sau cu şoc |
Întreruperea transmiterii sarcinii |
Evitarea apariţiei suprasarcinilor şi/sau montarea cu prestrângere pentru ca în timpul funcţionării să nu apară jocuri şi, deci, şocuri |
|
Rupera tijei şurubului la oboseală |
Scoaterea din uz |
Ruperea (fig. AFS-T.6.1,e; AFS-T.6.2,b) apare frecvent (aprox. 65%,) în zona primei spire a piuliţei în contact cu spira ca urmare a încărcării maxime (aprox 30%F, fig. AFS-T.6.1,a,b) |
Solicitările variabile şi concentratorul de tensiune de la baza dintelui (fig. AFS-T.6.2,c; tensiunile în zona interioară a filetului sunt maxime) |
Întreruperea transmiterii sarcinii |
Limitarea prin calcul a tensiunilor de oboseală la valori admisibile; măsuri constructive de diminuare a cauzelor
|
|
Deteriorarea filetului şurubului şi/sau piuliţei |
Demontare anevoioasă şi imposibilitatea de remontare |
În zona de contact a flancului filetului piuliţei şi şurubului |
Depăşirea rezistenţei la strivire a materialului piuliţei şi/sau şurubului |
Deformarea plastică a flancurilor filetului şi modificarea pasului acestuia în zona strânsă |
Limitarea prin calcul a tensiunilor de strivire în zonele spirelor în contact la valori admisibile |
Frecvenţa mare a ruperilor, de obicei, la oboseală în zona primei spire în contact cu piuliţa este explicabilă prin distribuţia neuniformă a sarcinii pe spire - prima spiră preia aprox. 35% din sarcină (fig. AFS-T.6.1,b) şi tensiunea în această zonă este de 5 ori mai mare decât în tijă (fig. AFS-T.6.1,a) - şi prin distribuţia neuniformă a tensiunilor (fig. AFS-T.6.1,c) în secţiunea şurubului cu valori maxime, mai ales a tensiunii axiale, în zona concentratorului de tensiune, racordarea din fundul filetului.
|
|
|
|
|
|
c |
|||
|
|
|
||
|
a |
b |
d |
e |
|
Fig. AFS-T.6.1 Solicitări şi cedări ale asamblărilor filetate: a – zone (secţiuni) critice; b – distribuţia sarcinii pe spirele piuliţei; c – variaţiile tensiunilor din tija şurubului; c – forma secţiunii în cazul ruperii la suprasarcini |
|||
|
|
|
|
|
a |
b |
c |
|
Fig. AFS-T.6.2 Forme de cedare a asamblărilor filetate: a – ruperea tijei la suprasarcini; b – ruperea tijei la oboseală; c – deformarea plastică a filetului |
||
AFS-T.7 PARMETRI FUNCŢIONALI ŞI CONSTRUCTIVI
|
|
Parametri geometrici principali: - diametrul nominal al filetului, d este diametrul exterior al filetului şurubului; - diametrul exterior al filetului piuliţei, D; - diametrul mediu al filetului şurubului şi piuliţei, d2 = D2 (diametrul cilindrului pe a cărei generatoare grosimile plinului şi golului sunt egale); - diametrul interior al filetului şurubului, respectiv piuliţei, d1, D2; - pasul filetului, p (distanţa dintre punctele omologe a două spire consecutive); - înălţimea profilului generator al filetului, H; - înălţimea efectivă a profilului filetului, H1; - înălţimea utilă a profilului filetului, H2 (înălţimea profilului în contact dintre spirele filetului şurubului şi piuliţei; - unghiul profilului filetului, α (α = 60o, pentru filete metrice; α = 55o, pentru filete Whitworth, în ţoli); - unghiul de înclinare a spirei filetului, β; este variabil, dependent de cilindrul pe care se consideră (fig. AFS-T.4.1,a,b); în calcule se foloseşte unghiul de înclinare corespunzător diametrului mediu, d2
Filetele conice se utilizează, în special, pentru asamblarea pieselor care necesită, în plus, şi o bună etanşare; acestea pot avea bisectoarea unghiului de vârf a profilului perpendiculară pe axa asamblării (fig. AFS-T.1,c) - acestea se pot asambla şi cu filete cilindrice - sau pe generatoarea suprafeţei conice (AFS-T.1,d) care se recomandă la presiuni şi temperaturi ridicate; elementele geometrice ale filetelor conice depind de planul de măsurare
|
|
|
a |
||
|
|
||
|
b |
||
|
|
|
|
|
c |
d |
|
|
Fig. AFS-T.7.1 Parametrii geometrici ai filetelor de fixare şi etanşare: a – cilindric; b – conic; c – conic perpendicular pe axa şurubului; d – conic perpendicular pe generatoare |
||
AFS-T.8 MODELE DE CALCUL
AFS-T.8.1 Modele de calcul a forţelor şi momentelor din asamblările filetate
AFS-T.8.1.1 Modele de calcul a forţelor şi momentelor din asamblările filetate nepretensionate
Tab. AFS-T.8.1.1.1 Model de calculul a momentului de înşurubare (deşurubare)
|
|
|
Ipoteze de calcul: - deplasarea piuliţei se asimilează cu deplasarea unui sector unghiular pe un plan înclinat tangent la cercul mediu; - distribuţia presiunilor pe suprafeţele în contact este uniformă şi forţa rezultantă se consideră concentrată într-un punct la nivelul unui cerc mediu. Forţe şi momente în filet (α > 0): - forţa axială exterioară, F; - forţa de reacţiune normală, N, rezultantă a presiunilor de contact dintre spirele piuliţei şi şurubului; - forţa normală în plan tangent, Fn, este componenta forţei N,
- forţa de frecare (sens opus vitezei relative între filetele şurubului şi piuliţei), Ff = µ N care ţinând cont de (AFS-T.8.1.1.1) devine,
unde,
µ este coeficientul de frecare;
- forţa de reacţiune radială, Fr, este componenta forţei N în planul radial perpendicular pe cel axial, x-x/y-y; - forţa de împingere a corpului piuliţei pe planul înclinat la înşurubare, H şi deşurubare, H’ se determină din relaţiile de echilibru a forţelor după acele x-x şi y-y:
care după luarea în considerare a relaţiei forţei de frecare, Ff devin
şi în urma prelucrării rezultă,
Similar, pentru deşurubare se obţine,
momentul de înşurubare, respectiv de deşurubare,
|
|||
|
a |
b |
||||
|
|
|
||||
|
c |
d |
||||
|
Fig. AFS-T.1.1.1 Scheme de calcul a forţelor şi momentelor în asamblarea filetată: a – schema generală; b – detaliu asamblare filetată; c – înşurubare (urcare pe planul înclinat); d – deşurubare (coborâre pe planul înclinat); |
|||||
|
Obs. a. În fig. AFS-T se prezintă modelul de calcul a forţelor şi momentelor pentru cazul filetului pătrat (α = 0), nefolosit pentru filetele de fixare dar se întâlnesc la filetele cuplelor elicoidale; relaţiile de calcul sunt cazuri particulare ale cazului general α > 0 de mai sus cu α = 0. |
|||||
|
|
|
|
Forţe şi momente în filetul pătrat (cazul particular, α = 0): - forţa axială exterioară, F; - forţa de reacţiune normală, N; - forţa de acţiune/reacţiune, R
-
forţa de frecare,
-
forţa de împingere a corpului piuliţei pe planul înclinat la înşurubare,
-
momentul de înşurubare, respectiv, de deşurubare
|
||
|
a |
b |
c |
|||
|
Fig. AFS-T.1.1.2 Scheme de calcul a forţe şi momentelor în asamblarea filetată cu profil pătrat (α = 0): a – schema generală; b – înşurubare (urcare pe planul înclinat); d – deşurubare (coborâre pe planul înclinat); |
|||||
|
Obs. Condiţia de
autofixare (autofrânare): piuliţa nu
trebuie să se desfacă de la sine sub acţiunea forţei F în
sensul deşurubării ei; din punct de vedere matematic această
condiţie este echivalentă cu una din inegalităţile, Md
> 0 sau H’
> 0,
din care rezultă,
pentru filetul cu α
> 0 sau
|
|||||
Tab. AFS-T.8.1.1.2 Model de calculul momentului de pivotare (de frecare dintre piuliţă şi piesa asamblată)
|
a
b
Fig. AFS-T.1.1.2 Schema de calcul a momentului de pivotare de frecare: a - cu forţă conecentrată (cazul I) , b - cu prsiunea uniform distribuită (cazul II) |
Ipoteze de calcul: - coeficientul de frecare dintre piuliţă şi piesa pe care aceasta se aşează, µ1, este constant; - presiunea se consideră distribuită uniform, pe suprafaţa de contact (fig. AFS-T.1.1.2, b),
unde d0 reprezintă diametrul găurii de trecere şi S – deschiderea (dimensiunea) cheii de strângere a piuliţei. Momentul de pivotare - model simplificat (cazul I, fig. AFS-T.1.1.2, a) Momentul de frecare de pivotare, considerând forţa normală pe suprafaţa de contact acţionând la nivelul cercului cu diametrul mediu dm, se determină cu relaţia,
Mp = µ1 F
Momentul de pivotare - model mai precis (cazul II, fig. AFS-T.1.1.2, b) Momentul de frecare de pivotare se determină, ţinând cont de distribuţia uniformă a presiunii (p = ct.) pe suprafaţa de contact (conform ipotezei de mai sus), cu relaţia,
care, ţinând cont de relaţia (AFS-T.8.1.1.1.6) devine,
Momentul şi forţa de acţiune asupra cheii (manivelei): Din ecuaţia de
echilibru a piuliţei (fig. AFS-T.1.1.1,a)
sau, considerând relaţia simplificată (AFS-T.8.1.1.1.7) a momentului de pivotare,
Mm = F rezultă relaţia de calcul a forţei de acţiune a cheii (fig. AFS-T.1.1.1,a),
sau, respectiv,
Fm = Obs.
Pentru valori medii statistice ale parametrilor din
relaţiile (AFS-T.8.1.1.1.12, (AFS-T.8.1.1.1.13)) şi în cazul utilizării cheilor
standardizate
|
AFS-T.8.1.2 Model de calcul a forţelor din asamblările filetate pretensionate
Tab. AFS-T.8.1.2.1 Model de calcul a asamblărilor cu şuruburi solicitate axial pretensionate
|
a
b c d
e f
g h
Fig. AFS-T.1.2.1 Scheme de calcul: a – structură şi încărcare; b – starea iniţial; c – starea cu prestrângere; d – starea de exploatare (cu acţiune externă); e – caracteristicile elastice ale şurubului şi piuliţei; f – caracteristica elastică a asamblării filetate pretensionată; g – caracteristica elastică a asamblării filetate pretensionată încărcată exterior cu sarcină statică; g – caracteristica elastică a asamblării filetate pretensionată încărcată exterior cu sarcină variabilă |
Ipoteze de calcul: - şuruburile de fixare a capacului recipientului sunt identice ca dimensiuni şi încărcări; - forţa exterrioară de exploatare se consideră statică, dar poate fi şi pulsatorie; - strângerea iniţială a asamblării trebuie să asigure menţinerea etanşeităţii şi în timpul funcţionării cu presiune în interiorul recipientului; - considerând, deformaţiile elementelor asamblării în domeniul elastic, rigidităţile şurubului şi a pieselor strânse se determină cu relaţiile:
în care, ψs şi ψp sunt unghiurile caracteristicilor elastice asociate şurubului şi, respectiv, pieselor strânse; aceste mărimi se determină prin calcul sau experimental. Montaj şi funcţionare - faza de premontaj (fig. AFS-T.1.2.1,b), se asamblează şuruburile şi piuliţele cu forţe mici până la eliminarea jocurilor şi neapariţia deformaţiilor în asamblare; - faza de montaj propriu-zis (fig. AFS-T.1.2.1,c,e,f), se strâng piuliţele cu cheia şi, ca urmare în elementele asamblării apare forţa de prestrângere, F0, ce solicită şuruburile la tracţiune şi le alungeşte cu săgeta δs, şi comprimă piesele asamblate cu săgeata δp, diferită de δs deoarece rigidităţile sunt diferite;
-
faza de exploatare (fig. AFS-T.1.2.1,d,g) se produce acţiunea
externă cu forţa, Fe, consecinţă a introducerii unui
fluid cu presiunea p în recipient, şi ca urmare şuruburile se alungesc
suplimentar cu săgeata
Relaţii de calcul a forţelor: Forţa
suplimentară care încarcă şurubul, Fsl, respectiv, forţa de
strângere în exploatare (remanentă) a pieselor,
şi
din care luând în considerare relaţiile (AFS-T.8.1.2.2), rezultă,
unde, s-a notat cu χ = ks/(ks + kp), rigiditatea asamblării. Din fig. AFS-T.1.2.1,g forţa axială care încarcă şurubul şi forţa axială care comprimă piesele după aplicarea forţei de exploatare Fe, se obţin, forţa axială totală din şurub,
şi forţa axială de strângere (remanentă) în exploatare, Condiţia de asigurare a etanşeităţii Pentru asigurarea
etanşeităţii în zona pieselor asamblate este necesar ca,
În cazul în care forţa de exploatare este variabilă, frecvent se întâlneşte, variaţia pulsatorie cu forţa maximă Fe max (fig. AFS-T.1.2.1,h), forţa axială totală din şurub maximă şi forţa de strângere (remanentă) minimă în exploatare sunt: Faş max = F0 + χ Fe max, (AFS-T.8.1.2.8)
În acest caz, condiţia de asigurare a etanşeităţii (AFS-T.8.1.2.7) devine, F0 ≥ (1 - χ)Fe max (AFS-T.8.1.2.10) |
||
|
Calculul rigidităţilor: Pentru şuruburile cu secţiune constantă, din expresia alungirii la tracţiune,
se obţine relaţia rigidităţii şurubului,
în care, As reprezintă aria secţiunii şurubului, Es – modulul de elasticitate al materialului şurubului, iar ls – lungimea activă a şurubului măsurată de la jumătatea înălţimii capului şurubului până la jumătatea înălţimii piuliţei. În cazul şuruburilor cu n secţiuni diferite rigiditatea se determină considerând şurubul cu n tronsoane cu secţiune constantă înseriate cu relaţia,
unde, ksi = Asi Es/ lsi – sunt rigidităţile tronsoanelor 1, 2…n cu Asi şi lsi - ariile secţiunilor şi respectiv, lungimile tronsoanelor şurubului. |
Rigiditatea pieselor asamblate se determină considerând că volumul de material care participă la transmiterea sarcinii este delimitat la exterior de două suprafeţe tronconice cu generatoarea înclinată cu unghiul γ (frecvent, 45o), iar la interior de suprafaţa locaşului de trecere a şurubului cu diametrul d0. Similar, considerând şi piesele asamblate ca tronsoane cilindrice (echivalente cu tronsoanele tronconice) înseriate, rigiditatea pieselor strânse se determină cu relaţia
în
care , kp1 = Ap1
Ep1/
lp1 este
rigiditatea tronsonului comprimat asociat capacului,
|
||
|
|
|
|
|
|
a |
b |
c |
|
|
Fig. AFS-T.1.2.2 Scheme de calcul a rigidităţilor pieselor asamblate: a – şurub cu piuliţă; b – prezon cu piuliţă; b – prezon cu piuliţă şi garnitură de etanşare |
|||
AFS-T.8.2 Model de calcul de rezistenţă a asamblării filetate
|
Fig. AFS-T.2.1.1 Scheme de calcul a filetelor şi asamblării filetate |
Ipoteze de calcul: - sarcina axială F se repartizează uniform asupra celor z spire ale piuliţei aflate în contact cu spirele piuliţei; - sarcina F/z ce revine unei spire se consideră uniform distribuită pe suprafaţa de contact cu presiunea pm cu direcţia paralelă cu axa filetului. Condiţia de rezistenţă la strivire a asamblării filetate:
în
care, σas = min( Condiţiile de rezistenţă la forfecare a filetului şurubului şi piuliţei:
în
care,
Condiţiile de rezistenţă la încovoiere a filetului şurubului şi piuliţei:
în
care,
|
|
Obs. Verificarea asamblării filetate şi a spirelor filetelor şurubului şi piuliţei se face numai în cazul folosirii filetelor nestandardizate; pentru filetele standardizate nu sunt necesare calculele de mai sus deoarece înălţimea piuliţei a fost determinată impunându-se condiţia de egală rezistenţă a tijei şurubului şi a spirelor filetate rezultând pentru piuliţă o cu înălţiimea m=0,8d. |
|
AFS-T.8.3 Modele de calcul de rezistenţă a asamblărilor cu şuruburi
AFS-T.8.3.1 Modele de calcul de rezistenţă a asamblărilor cu şuruburi solicitate axial
Tab. AFS-T.8.3.1.1 Model de calcul de rezistenţă a asamblării cu şurub solicitată axial centric
|
|
Ipoteze de calcul:
-
tija şurubului, în cazul cel mai
defavorabil (strângerea sub sarcină), este solicitată la tracţiune
de forţa Faş şi la torsiune de momentul de
înşurubare,
- secţiunea critică, circulară cu diametrul egal cu diametrul interior al filetului d1, corespunde zonei primei spire a piuliţei. Condiţia de rezistenţă la solicitări compuse (tracţiune şi torsiune) a tijei şurubului:
unde, σat = σ02/c este tensiunea admisibilă la tracţiune cu σ02 este tensiunea de curgere a materialului şi c – coeficientul de siguranţă (frecvent, c = 2,5); pentru tijele şuruburilor standard σ02 se determină din grupa de caracteristici mecanice (v. subcap. AFS-T.5). Obs. Pentru proiectare, se aproximează aportul tensiunii de torsiune în tensiunea echivalentă prin factorul β = 1…1,3 [Jula, 1986] şi relaţia AFS-T.8.3.1.1.1 devine,
relaţie simplificată de verificare din care se poate determina diametrului d1, pentru dimensionare |
|
Fig. AFS-T.8.3.1 Schema de calcul a asamblării cu şurub solicitat axial centric |
Tab. AFS-T.8.3.1.2 Model de calcul de rezistenţă a asamblării cu şuruburi solicitată axial centric
|
|
|
Ipoteze de calcul: - forţa exterioară axială (statică sau variabilă) acţionează în centrul axelor şuruburi care se consideră că au axele paralele; - cele z şuruburi sunt montate cu şoc sunt strânse identic; - forţa exterioară se împarte egal pe şuruburile asamblării (care pot fi şi pretensionate) şi forţa axială dintr-un şurub, Faş = Fa/z; - calculul de rezistenţă al asamblării cu şuruburi solicitată axial centric se reduce la calculul asamblării cu şurub.
Relaţiile calcul a asamblării cu z şuruburi solicitată axial centric sunt cele din Tab. AFS-T.8.3.1.1 în care se consideră, Faş = Fa/z, meţinând ca valabile ipotezele adoptate
|
|
a |
b |
|
|
Fig. AFS-T.8.3.2.1 Schema de calcul de rezistenţă a asamblării cu şuruburi solicitată axial centric: a – schema de încărcare exterioară; b – schema încărcării unui şurub |
||
Tab. AFS-T.8.3.1.3 Model de calcul de rezistenţă a asamblării cu şurub solicitată axial exentric
|
Fig. AFS-T.8.3.1.2.2 Schema de calcul de rezistenţă a tijei şurubului solicitat axial excentric |
Ipoteze de calcul:
-
tija şurubului, în cazul cel mai
defavorabil (strângerea sub sarcină) este solicitată la tracţiune
de forţa Faş, la încovoiere de momentul Mi
=
Faşe şi la torsiune de momentul înşurubare,
- secţiunea critică, circulară cu diametrul egal cu diametrul interior al filetului d1, corespunde zonei primei spire a piuliţei. Condiţia de rezistenţă la solicitări compuse (tracţiune, încovoiere şi torsiune) a tijei şurubului:
unde: σat = σ02/c reprezintă tensiunea admisibilă la tracţiune cu σ02 este tensiunea de curgere a materialului şi c – coeficientul de siguranţă
|
|||
|
|
|
|
Obs. a. Dacă se neglijează solicitarea de torsiune relaţia tensiunii echivalente (AFS-T.8.3.1.3.1) devine,
din care, se poate deduce că pentru e = d1, σtot = 9 σt şi, deci, tensiunea de încovoiere are o pondere foarte mare şi se impune evitarea, pe cât posibil a acestor tipuri de asamblări; b. în cazul în care suprafeţele de rezemare a piuliţei şi/sau şurubului nu sunt perpendiculare pe axa găurii (fig. AFS-T.8.3.1.3.3) efectul încovoierii tijei este semnificativ şi pentru diminuarea acestuia se iau măsuri de prelucrare a suprafeţelor de reazem (AFS-T.8.3.1.2.3,b) sau în cazul profilelor laminate U sau I utilizarea de şaibe speciale (AFS-T.8.3.1.2.3,c) |
|
|
a |
b |
c |
||
|
Fig. AFS-T.8.3.1.2.3 Evitarea solicitării la încovoiere a tijei şurubului: a – efectul neperpendicularităţii suprafeţelor de reazem; b – prelucrarea suprafeţei de reazem; c – folosirea de şaibe speciale pentru profile U |
||||
Tab. AFS-T.8.3.1.4 Model de calcul de rezistenţă a asamblării cu şuruburi solicitată axial excentric
|
a
b
Fig. AFS-T.8.3.1.2.4 Scheme de încărcare a şuruburilor unei asamblări solicitată excentric: a – generală; b – cu componentele (forţa şi momentul) torsorului de reducere |
Ipoteze de calcul: - şuruburile fiind identice ca geometrie şi ca material au aceeaşi rigiditate, kş; - acţiunea forţei exterioare (fig. AFS-T.8.3.1.2.4,a) se reduce la o încărcare cu forţa F în centrul axelor şuruburilor care produce în fiecare din cele 6 şuruburi o forţă axială Fş = F/6 (fig. AFS-T.8.3.1.2.4,b) şi, în plus, la o încărcare cu momentul Me care produce forţe axiale suplimentare Fşi (i = 1,2,3); - având în vedere deformaţiile elastice ale şuruburilor flanşa (considerată cu rigiditate infinită) se roteşte cu unghiul, θ, în jurul liniei de reazem ce trece prin punctul O (fig. AFS-T.8.3.1.2.4,c); în acest caz alungirile tijelor şuruburilor din fiecare rând, δ1, δ2 şi δ3 sunt, pe de-o parte, proporţionale cu distanţele, L1, L2 şi, respectiv, L3, conform relaţiilor: δ1/L1= δ2/L2= δ3/L3= tgθ, şi, pe de altă parte, proporţionale cu forţele din şuruburi Fş1, F ş2 şi, respectiv, Fş3, conform relaţiilor: Fş1/δ1 = Fş2/δ2 = Fş3/δ3 = kş, din care rezultă,
- se neglijează solicitările de încovoiere din tijelele şuruburilor. Relaţii de calcul a forţelor suplimentare din şuruburi: Din ecuaţia de echilibru a momentelor în punctul de reazem O, considerând două şuruburi pe un rând,
şi ţinând cont de relaţia (AFS-T.8.3.1.2.3) se obţin,
unde Fş1, Fş2 şi Fş3 sunt forţele suplimentare generate de momentul Me în şuruburile de pe rândurile 1, 2, respectiv, 3. Forţele axială rezultantă din şuruburile i = 1,2,3 sunt
Faşi = Fşi + Fş = Fşi + F/6. (AFS-T.8.3.1.3.8)
În cazul general, al asamblării cu n rânduri de şuruburi şi m şuruburi pe un rând (p = m.n) forţele axiale rezultante din şuruburile celor i = 1,2,3... n rânduri se determină din relaţia,
Calculul de rezistenţă al asamblării cu şuruburi solicitată axial excentric se reduce la calculul şurubului cel mai solicitat încărcat cu forţa axială, Faş = max (Faş1, Faş2… Faşm), conform modelului din tab. AFS-T.8.3.1.1 |
AFS-T.8.3.2 Modele de calcul de rezistenţă a asamblării cu şuruburi solicitată transversal
Tab. AFS-T.8.3.2.1 Model de calcul de rezistenţă a asamblării cu şurub montat fără joc solicitată transversal
|
|
|
|
|
|
c |
|||
|
|
|||
|
a |
b |
d |
|
|
Fig. AFS-T.8.3.2.1 Scheme de calcul a asamblării cu şurub montat fără joc: a – solicitată transversal necentrat; b – solicitată transversal centrat; c – distribuţia uniformă a presiunii; d – distribuţia cosinusoidală a presiunii |
|||
|
Ipoteze de calcul: - direcţia forţei de încărcare exterioară, Ftş, este perpendiculară pe axa şurubului; - şurubul este montat fără joc (păsuit) formând un alezaj intermediar (distribuţia cosinusoidală a presiunii, fig. AFS-T.8.3.2,c) sau cu strângere redusă (distribuţia uniformă a presiunii, fig. AFS-T.8.3.2.1,d); - sarcina exterioară Ftş se transmite de la tabla 1 la tabla 2 (fig. AFS-T.8.3.2.1,a) sau de la tablele 1 şi 1’ la tabla 2 (fig. AFS-T.8.3.2.1,b) prin contacte directe (semicilindrice), conform fluxurilor: 1 -> tijă şurub -> 2, respectiv, 1 şi 1’ -> tijă şurub -> 2. Condiţiile de rezistenţă a asamblării: - condiţia de rezistenţă la strivire (contact) şurub-piese asamblate: pentru distribuţia presiunii uniformă (fig.
AFS-T.8.3.2.1,c), sau respectiv, cosinusoidală (fig. AFS-T.8.3.2.1,d),
unde: lmin = min(l1, l2),
pentru cazul din fig. AFS-T.8.3.2.1,a sau ,
|
- condiţia de rezistenţă la forfecare a tijei şurubului:
unde, τaf este tensiunea admisibilă la forfecare a materialului şurubului τaf = (0,6…0,8)σat, valorile maxime sunt pentru sarcini variabile); i =1 sau 2, numărul zonelor de forfecare pentru cazul din fig. AFS-T.8.3.2.1,a sau respectiv fig. AFS-T.8.3.2.1,b.
Obs. Comparativ cu asamblările cu şuruburi montate cu joc (subcap. AFS-T.8.3.2.2) în cazul acestor asamblări se obţin şuruburi de dimensiuni mai mici, dar tehnologia este mai pretenţioasă (tija şurubului se rectifică, iar găurile se alezează) şi precizia necesară este mult mai ridicată şi, deci, costuri mult mărite. |
||
Tab AFS-T.8.3.2.2 Model de calcul de rezistenţă a asamblării cu şurub montat cu joc solicitată transversal
|
|
|
|
|
|
a |
b |
c |
|
|
Fig. AFS-T.8.3.2.2 Scheme de calcul a asamblării cu şurub montat cu joc: a – solicitată transversal necentrat; b – solicitată transversal centrat; c – echilibrul forţelor pentru cazul a |
|||
|
Ipoteze de calcul: - direcţia forţei de încărcare exterioară, Ftş, este perpendiculară pe axa şurubului; - şurubul este montat cu joc mare (nu există contacte între table şi tija şurubului); - forţa transversală, Ftş, se transmite de la tabla 1 la tabla 2 (fig. AFS-T.8.3.2.2,a) sau de la tablele 1 şi 1’ la tabla 2 (fig. AFS-T.8.3.2.2,b) prin frecare, consecinţă a strângerii tablelor cu forţa axială din şurub Faş, fără să apară mişcare relativă şi contact cu tija şurubului. Condiţia de transmitere a forţei prin frecare:
Ff = µ Faş i ≥ βa Ftş (AFS-T.8.3.2.2.1)
unde, i este numărul suprafeţelor de frecare, i = 1, pentru cazul din fig. AFS-T.8.3.2.2,a şi i = 2, pentru cazul din fig. AFS-T.8.3.2.2,b; µ - coeficientul de frecare; βa – factor de siguranţă la alunecare a tablelor. |
Calculul de rezistenţă a şurubului În cazul, îndeplinirii condiţiei de transmitere a forţei prin frecare, şuruburile sunt solicitate la tracţiune iar în timpul montajului şi la torsiune de momentul de înşurubare; forţa axială dintr-un şurub se determină din relaţia (AFS-T.8.3.2.2.1),
Calculul asamblării cu şuruburi montate cu joc solicitată transversal se reduce la calculul asamblării cu şurub solicitată axial centric conform modelului din tab. AFS-T.8.3.1.1 considerând încărcarea din relaţia (AFS-T.8.3.2.2.2). Obs. Deoarece forţa de strângere este mai mare decât forţa de transmis rezultă şuruburi de diametre mari ceea ce reprezintă un dezavantaj; avantajul acestor asamblări constă în faptul că necesită o precizie de prelucrare scăzută a şuruburilor şi alezajelor în care se montează. |
||
Tab AFS-T.8.3.2.3 Model de calcul de rezistenţă a asamblărilor cu şuruburi (montate cu sau fără joc) solicitate transversal centric
|
Fig. AFS-T.8.3.2.2.1 Schema de calcul a asamblărilor cu şuruburi solicitate transversal centric |
Ipoteze de calcul:
-
şuruburile au axele paralele cu o
axa care conţine centrul acestora, CA, în care
- şuruburile, consecinţă a încărcării cu forţa exterioară F cu direcţia ce trece prin punctul CA, sunt încărcate cu forţe transversale egale,
sau, pentru cazul general cu z şuruburi,
- calculul asamblărilor cu şuruburi montate cu joc solicitate transversal centric, în final, se reduce la calculul asamblării cu şurub (montat fără joc sau cu joc) conform modelelor din tab. AFS-T.8.3.2.1 sau, respectiv, tab. AFS-T.8.3.2.2 încărcată cu forţa transversală, Ftş. |
Tab. AFS-T.8.3.2.4 Model de calcul de rezistenţă a asamblărilor cu şuruburi solicitate transversal excentric
|
|
|||
|
a |
b |
c |
|
|
Fig. AFS-T.8.3.2.4.1 Schema de calcul a asmblării cu şuruburi solicitate transversal excentric: a – schema generală; b – schema încărcării cu forţa redusă; b – schema încărcării cu momentul redus |
|||
|
a
b Fig. AFS-T.8.3.2.4.2 Scheme de încărcare axial a şuruburilor montate cu joc din asamblarea solicitată transversal excentric: a – structura necentrată; b – structura centrată
|
Ipoteze de calcul:
-
şuruburile au axele paralele cu o
axa care conţine centrul acestora, CA, în care
- forţa exterioară transversală, F, care acţionează excentric asupra asamblării se reduce la nivelul axei care trece prin punctul CA la o forţă egală F şi la momentul, Me = F e; (AFS-T.8.3.2.4.1) - forţa F se transmite în cote egale cu F/4 de fiecare şurub (fig. AFS-T.8.3.2.3.1,b) şi momentul Me prin forţele Fm1, Fm2, Fm3 şi Fm4 ale căror momente respectă relaţia,
în care,
- forţele Fm1, Fm2, Fm3 şi Fm4 sunt proporţionale cu distanţele (braţele), r1, r2, r3 şi, respectiv, r4, conform relaţiei,
în care K este o constantă oarecare; - şuruburile, consecinţă a încărcării din punctul CA, cu forţa F şi momentul Me, sunt încărcate cu forţele transversale Ft1, Ft2, Ft3 şi Ft4 care se obţin prin însumarea vectorială a forţelor asociate cotei F/4 cu forţele Fm1, Fm2, Fm3 şi, respectiv, Fm4 (fig. AFS-T.8.3.2.4.1,a). Relaţii de calcul a forţelor transversale de încărcare a şuruburilor: Din relaţiile (AFS-T.8.3.2.4.1), (AFS-T.8.3.2.4.2) şi (AFS-T.8.3.2.4.3) rezultă, forţele care generează componentele momentului Me,
unde, i = 1, 2, 3, 4. Prin însumare, conform “regulii paralelogramului”, forţele rezultante de încărcare a şuruburilor se determină cu relaţia (fig. AFS-T.8.3.2.4.1),
unde, i = 1, 2, 3, 4 şi forţele Fmi sunt conform relaţiei (AFS-T.8.3.2.4.4); θi - unghiurile direcţiilor forţelor Fmi (fig. AFS-T.8.3.2.4.1,a) |
||
|
Relaţia de calcul a forţelor de încărcare axial a şuruburilor, i = 1,2,3,4, montate cu joc (fig. AFS-T.8.3.2.4.2):
unde, j = 1 (fig. AFS-T.8.3.2.4.2,a) sau j = 2 (fig. AFS-T.8.3.2.4.2,b) reprezintă numărul suprafeţelor de frecare, z – numărul de şuruburi; µ - coeficientul de frecare; βa – factor de siguranţă la alunecare a tablelor, Fti - forţa transversală de încărcare a şurubului i. Calculul de rezistenţă a asamblărilor cu şuruburi montate cu joc solicitate transversal excentric, în final, se reduce la calculul asamblării cu şurub (montat fără joc sau cu joc) conform modelelor din tab. AFS-T.8.3.2.1 sau, respectiv, tab. AFS-T.8.3.2.2 încărcată cu forţa transversală, Ftş = max (Ft1, Ft2, Ft3, Ft4), pentru asamblarea cu şurub montat fără joc, sau respectiv, forţa axială maximă, Faş = max (Faş1, Faş2, Faş3, Faş4), pentru asamblarea cu şurub montat cu joc |
|||
|
Fig. AFS-T.8.3.2.4.3 Schema de calcul a centrului axelor paralele asociate şuruburilor şi de generalizare privind direcţia forţei exterioare |
Obs. 1. Coordonatele centrului axelor şuruburilor, CA, se pot defini ca centrul axelor paralele asociate şuruburilor asamblării: a. pentru cazul figurilor simple (triungi, pătrat, romb, paralelogram) se folosesc proprietăţile geometriei elementare; b. pentru cazul general (fig. AFS-T.8.3.2.4.2 ) când se cunosc coordonatele punctelor asociate axelor şuruburilor (Xi, Yi) în raport cu sistemul de coordonate XOY se determină coordonatele centrului axelor,
şi coordonatele centrelor axelor în raport cu sistemul de coordonate xCAy rotit cu unghiul α faţă de sistemul de coordonate XOY,
2.
Pentru cazul general al
încărcării asamblării cu forţele ortogonale FX
şi FY raportate la sistemul de coordonate XOY se
determină forţa rezultantă,
|
||
AFS -T.9 STRUCTURI CONSTRUCTIVE
AFS -T.9.1 Formele constructive ale şuruburilor, piuliţelor şi şaibelor plate
|
|
|
|
|
|
|
|
a |
b |
c |
d |
e |
|
|
|
|
|
|
|
|
|
f |
g |
h |
i |
j |
|
|
|
|
|
|
|
|
|
k |
l |
m |
n |
o |
p |
|
|
|
|
|
||
|
r |
s |
t |
u |
||
|
Fig. AFS-T.9.1.1 Forme constructive ale capului şurubului: a – hexagonal; b – hexagonal cu prag intermediar; c – hexagonal cu guler; d – pătrat; e – cilindric cu locaş hexagonal interior; f – cap cilindric cu crestătură; g – semirotund cu crestătură; h – semiînecat cu crestătură; i – înecat cu locaş în cruce; j – bombat şi pătrat antirotire ; k – bombat şi nas antirotire; l – înecat cu crestătură; m – fără cap cu crestătură; n – fără cap locaş hexagonal interior; o– inel (ochi); p – cilindric striat; r – ciocan (în T); s – cârlig pentru fundaţie; t – spintecat pentru fundaţie; u – inelar |
|||||
|
Obs. - capul hexagonal (fig. AFS-T.9.1,a,b,c) asigură cel mai redus spaţiu de manevrare la montare/demontare cu cheia fixă; - capul pătrat (fig. AFS-T.9.1,d) asigură suprafaţa de contact cu cheia de montare/demontare mai mare şi are durabilitate ridicată la montări/demontări repetate; - capul hexagonal cu prag intermediar (fig. AFS-T.9.1,b) asigură un concentrator de tensiune redus; - capul hexagonal cu guler (fig. AFS-T.9.1,c) se foloseşte pentru asamblarea pieselor din materiale moi (lemn, aluminiu etc.) pentru reducerea presiunii de contact pe suprafaţa de aşezare; - capul cu locaş hexagonal interior (fig. AFS-T.9.1,e) este utilizat pentru forţe de strângere mari iar capul cu locaş în cruce sau cu crestătură (fig. AFS-T.9.1,f,g,h,i,l,m,n) pentru şurubelniţă sunt utilizate pentru forţe de strângere reduse; - capul cu pătrat sau nas antirotire deformează materialul (de obicei, lemn) pieselor şi împiedică rotirea odată cu strângerea piuliţei; - formele din fig. AFS-T.9.1,o,p,r se folosesc în construcţia dispozitivelor tehnologice; - formele din fig. AFS-T.9.1,s,t se folosesc pentru fixarea la fundaţie prin îngropare în beton; - capul cilindric striat (fig. AFS-T.9.1,p) este utilizat pentru strângere cu forţe reduse cu mâna; |
|||||
|
|
|
|
|
|
|
|
|
a |
b |
c |
d |
e |
f |
g |
|
Fig. AFS-T.9.1.2 Forme constructive ale tijei şurubului: a – filetată pe toată lungimea; b,c – filetată numai pe o porţiune; d – cu porţiune de păsuire; e, f – subţiată cu porţiuni de ghidare; g – subţiată cu alezaj |
||||||
|
Obs. - diametrul porţiunii filetate poate fi mai mic (fig. AFS-T.9.2,d) când solicitarea în această zonă este mai redusă şi astfel se diminuează concentratorul de tensiuni; - diametrul porţiunii nefiletate poate fi mai mare (fig. AFS-T.9.2,d) decât al celei filetate pentru a se putea asigura zone de păsuire cu contact direct cu piesele asamblate; - pentru mărirea elasticităţii tijelor şuruburilor supuse la solicitări variabile se micşorează diametrul tijei nefiletate mai puţin în zonele de ghidare în alezajul din piesele asamblate (fig. AFS-T.9.2,e,f) sau se aplică o gaură axială (fig. AFS-T.9.2,g); - porţiunile de racordare de la tija filetată la cea nefiletată cu raze mărite (fig. AFS-T.9.2,e,f) sau cu racordare (fig. AFS-T.9.2,g) asigură o mărire a rezistenţei la oboseală; |
||||||
|
|
|
|
|
|
|
a |
b |
c |
d |
e |
|
Fig. AFS-T.9.1.3 Şuruburi speciale: a – pentru asamblarea tablelor; b – autofiletante; c – autoburgiere; d – holşurub; e – cu garnituri elicoidale (Heli Coil) |
||||
|
Obs. - pentru asamblarea tablelor subţiri cu grosimi comparabile cu pasul filetului se va practica o gaură de trecere în tabla de sub capul şurubului şi o gaură cu diametrul egal cu diametrul interior al filetului în cea de-a doua tablă cu grosimea mai mică decât pasul şurubului (fig. AFS-T.9.1.3,a); - pentru micşorarea costurilor asamblărilor în cazul elementelor din materiale moi (inclusiv din oţel) spira şurubului este configurată şi durificată prin tratament termic ca să poată, la înşurubare, să execute filetul, şi deci, şi strângerea (fig. AFS-T.9.1.3,b) sau, în plus, şurubul poate avea vârf de burghiere pentru prelucrarea alezajului (fig. AFS-T.9.1.3,c); - pentru a mări eficienţa asamblărilor filetate din piese masive din materiale moi se introduce între şurub şi piuliţă o garnitură elicoidală cu secţiune rombică (fig. AFS-T.9.1.3,d) care are rolul de a uniformiza repartiţia sarcinii pe spirele în contact. |
||||
|
|
|
|
|
|
a |
b |
c |
d |
|
Fig. AFS-T.9.1.4 Forme constructive de prezoane: a – tija nefiletată are acelaşi diametru cu tija filetată şi fără racordări; b – tija nefiletată are acelaşi diametru cu tija filetată şi o racordare de trecere ; c – tija nefiletată are acelaşi diametru cu tija filetată şi două racordări; d – tija nefiletată are diametrul mai mic |
|||
|
Obs. - prezoanele sunt tije cilindrice filetate la ambele capete care se utilizează în cazul când materialul unei piese nu asigură durabilitatea suficientă a filetului, la montări şi demontări frecvente, sau când din considerente constructive nu se pot folosi piuliţe; - lungimea porţiunii filetate în piesa de bază se determină în funcţie de caracteristicile materialelor acesteia (aluminiu, fontă, oţel etc.) |
|||
|
|
|
|
|
|
|
|
|
||||||
|
a |
b |
c |
d |
e |
f |
g |
h |
||||||
|
|
|
|
|
|
|
|
|||||||
|
i |
j |
k |
l |
m |
n |
o |
|||||||
|
Fig. AFS-T.9.1.5 Forme constructive de piuliţe: a – hexagonală obişnuită (forma A); b – hexagonală obişnuită (forma B); c – hexagonală cu guler; d,e – crenelată; f – pătrată; g – rotundă cu caneluri; h – rotundă cu găuri radiale; i – rotundă cu găuri radiale j – pentru canale T; k – hexagonală cu suprafaţă de aşezare sferică; l, m – înfundată; n – striată; o – fluture |
|||||||||||||
|
Obs. - piuliţa hexagonală cu suprafaţa sferică de aşezare (fig. AFS-T.9.5,k) permite centrarea piuliţei la axa şurubului şi este utilizată la montarea roţilor vehiculelor; - piuliţa rotundă cu caneluri (fig. AFS-T.9.5,g) se utilizează pentru fixarea axială a inelelor interioare ale rulmenţilor |
|||||||||||||
|
|
|
|
|
|
|
|
a |
b |
c |
d |
e |
f |
|
Fig. AFS-T.9.1.6 Forme constructive ale tijei filetate în zona cap : a – plată; b – bombată; c – cu vârf conic; d – cu cep cilindric plat; e – cu cep cilindric conic; f – cu cilindric şi con g – cu con interior |
|||||
|
Obs. Se folosesc ca ştifturi filetate pentru împiedicarea deplasării relative a unor piese prin intermediul contactelor dintre suprafeţele de cap şi locaşurile asociate (aplatisare, gaură conică, gaură cilindrică) |
|||||
|
|
|
|
|
|
a |
b |
c |
d |
|
Fig. AFS-T.9.1.7 Forme constructive de şaibe: a – plată circulară; b – de compensare pătrată pentru profil I; c – de compensare pătrată pentru profil U; d – de compensare sferice |
|||
|
Obs. Şaibele (rondelele) se folosesc pentru micşorarea presiunii pe suprafaţa de sprijin a piuliţei (fig. AFS-T.9.7,a) sau pentru aşezarea corectă a piuliţei când suprafaţa de reazem este neprelucrată sau înclinată (fig. AFS-T.8.3.1.2.2; fig. AFS-T.9.7,b – pentru asamblarea profilor laminate I, AFS-T.9.7,c – pentru profile U) |
|||
AFS -T.9.2 Soluţii pentru optimizarea constructivă a asamblărilor filetate şi cu şuruburi
Scop: asigurarea unor forme adecvate şi dimensiuni minime pentru a elimina majoritatea cazurilor de ruperi, în special, prin oboseală în condiţii de costuri reduse.
|
|
|
|
|
|
a |
b |
c |
d |
|
|
|||
|
Fig. AFS-T.9.2.1 Soluţii constructive de siguranţă şi centrare a asamblărilor cu joc solicitate transversal: a – stare funcţională necorespunzătoare; b – inele de centrare; c – cu tronson de centrare; d – cu prag de centrare |
|||
|
|
|
|
|
|
a |
b |
a |
b |
|
Fig. AFS-T.9.2.2 Soluţii constructive de uniformizare a repartizării forţei exterioare pe spirele în contact: a – piuliţă elastică comprimată; b – piuliţă elastică întinsă |
Fig. AFS-T.9.2.3 Efectele micşorării rigidităţii şuruburilor asupra comportării asamblărilor şu şuruburi solicitate axial pretensionate: a – caracteristica şi variaţia pulsatorie a forţei exterioare; b – caracteristica asamblării |
||
|
Obs. a. în cazul variantelor constructive de elasticizare a corpului piuliţei pentru uniformizarea repartizării forţei exterioare pe spirele în contact se obţin încărcări ale primei spire de până la 20% (fig. AFS-T.9.2.2) spre deosebire de cazul repartizării pentru piuliţa rigidă unde valoarea încărcării primei spire este 30…40% (fig. AFS-T.6.1); b. în cazul asamblărilor solicitate axial pretensionate, utilizarea de şuruburi cu elasticitate mărită (AFS-T.9.1.2, e,f,g) conduce la micşorarea forţei suplimentare, Fsl (inclusiv amplitudinii acesteia) şi a forţei totale Fs (fig. AFS-T.9.2.3,b) care încarcă şurubul comparativ cu utilizarea unor şuruburi cu secţiune constantă (AFS-T.9.1.2,b) încărcate de aceeaşi forţă exterioară F şi cu acelaşi mod de variaţie (pulsator). |
|||
|
|
|
|
|
|
a |
b |
c |
d |
|
Fig. AFS-T.9.2.4 Soluţii constructive de racordare cap-tijă: a –cu una sau două raze; b – cu rază şi tronson conic; c, d – cu degajare, tronson de păsuire şi rază; |
|||
|
Obs. Prin adoptarea uneia din soluţiile de mai sus se micşorează mult pericolul ruperii tijei în zona capului şurubului. |
|||
AFS -T.9.3 Asigurarea asamblărilor filetate împotriva autodesfacerii
Scop: evitarea autodesfacerii asamblării filetate care deşi îndeplineşte condiţia de autofixare (rel. AFS-T.8.1.1.6) se pot desface datorită acţiunilor sarcinilor variabile şi cu şoc, vibraţiilor şi diferenţelor de temperatură care au ca efect reducerea frecării din asamblare.
Principiile care stau la baza soluţiilor constructive de asigurare sunt:
- mărirea forţelor de frecare dintre elementele asamblării;
- împiedicarea rotirii relative a piuliţei faţă de şurub prin intermediul unor elemente suplimentare;
- deformarea plastică locală a materialului şurubului şi/sau piuliţei sau aplicarea de adaos de material (de obicei, puncte de sudură)
|
|
|
|
Descriere: Fig. AFS-T.9.3.1,a: prin strângerea contrapiuliţei se crează presiuni suplimentare între spirele piuliţei şi şurubului care se menţin şi în cazul anulării forţei exterioare datorită încărcării variabile, vibraţiilor şi/sau variaţiilor de temperatură. Fig. AFS-T.9.3.1,b: contrapiuliţa elastică asigură după strângere cu cheia datorită diferenţei de pas a porţiunii exterioare o încărcare cu o forţă axială locală care generează o forţa de frecare independentă de încărcarea exterioară. Fig. AFS-T.9.3.1,c,d: prin strângerea cu cheia partea superioară filetată se deformează în raport cu partea inferioară şi se produce o forţă elastică care solicită local şurubul şi generează forţă de frecare independentă de încărcarea exterioară. Fig. AFS-T.9.3.1,e: contrapiulița conică spintecată creează prin strângere în filetul piuliţei inferioare forţe suplimentare axiale şi o puternică presiune radială. Fig. AFS-T.9.3.1,f: piuliţa sau şurubul conţin inserţii, de obicei din nylon, care ca urmare a deformării la strângere asigură forţe de frecare mărite. Fig. AFS-T.9.3.1,g: piuliţa din tablă cu autostrângere, folosită la asamblarea elementelor caroseriilor autovehiculelor, are doi dinţi ce îndeplinesc rolul de filet şi la strângere se comprimă şi apasă pe filetul şurubului generând frecări care se opun desasamblării. Fig. AFS-T.9.3.1,h: prin strângerea şurubului tangenţial se generează în filetul piuliţei secţionată radial forţe de apăsare în filet mărite. Fig. AFS-T.9.3.2: muchiile dinţilor şaibelor şi capetele răsfrânte ale șaibelor Grower contribuie la împiedicarea rotirii piuliţei şi prin deformarea locală a suprafeţelor cu care vin în contact. |
|||||
|
a |
b |
c |
||||||
|
|
|
|
|
|
||||
|
d |
e |
f |
g |
h |
||||
|
Fig. AFS-T.9.3.1 Soluţii constructive de asigurare împotriva autodesfacerii prin mărirea forţelor de frecare : a – cu contrapiuliţă; b – cu piuliţă elastică masivă; c – cu contrapiuliţă elastică lamelară; d – cu contrapiuliţă elastică ambutisată; e – cu contrapiuliţă conică elastică; f – cu inserţii elastice; d – piuliţă elastică din tablă; g – piuliţă secţionată |
||||||||
|
|
|
|
|
|||||
|
a |
b |
c |
d |
|||||
|
Fig. AFS-T.9.3.2 Soluţii constructive de asigurare împotriva autodesfacerii prin mărirea forţelor de frecare cu şaibe elastice : a – plană dinţată la exterior; b – plană dinţată la interior; c – conică cu dinţi exteriori; d – Grower |
||||||||
|
|
|
|
|
|
|
|
a |
b |
c |
d |
e |
f |
|
Fig. AFS-T.9.3.3 Soluţii constructive de asigurare împotriva autodesfacerii prin elemente suplimentare: a – prin cui spintecat (şplint); b – ştift deformat în piuliţă crenelată; c – placă profilată pe întreg conturul; d – placă profilată pe semicontur; e – şaibă cu două aripioare; f – şaibă de siguranţă pentru piuliţele cu caneluri ale rulmenţilor |
|||||
|
|
|
|
|
a |
b |
c |
|
Fig. AFS-T.9.3.4 Soluţii constructive de asigurare împotriva autodesfacerii prin deformare plastică sau sudură: a – deformare plastica; b – sudură şurub de piuliţă; c – sudură piuliţă în raport cu piesa strânsă |
||