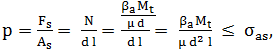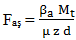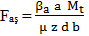AAB. ASAMBLĂRI ARBORE-BUTUC
AAB-T. CONSTRUCȚIA ȘI MODELAREA ASAMBLĂRILOR ARBORE-BUTUC
AAB-T.1 ASAMBLĂRI PRIN FRECARE
AAB-T.2.2
ASAMBLĂRI PRIN STRÂNGERE PE CILINDRU (BRĂȚARĂ)
|
CUPRINS |
|
AAB-T.2.2.1 DEFINIRE AAB-T.2.2.2 STRUCTURA CONSTRUCTIVĂ AAB-T.2.2.3
DOMENII DE UTILIZARE, AVANTAJE ȘI DEZAVANTAJE AAB-T.2.2.4 CLASIFICARE AAB-T.2.2.5 MATERIALE ȘI TEHNOLOGII AAB-T.2.2.6 FORME ȘI CAUZE DE SCOATERE DIN UZ SAU DE
COMPORTARE NECORESPUNZĂTORE AAB-T.2.2.7 PARAMETRII FUNCȚIONALI ȘI CONSTRUCTIVI AAB-T.2.2.8 MODELE DE CALCUL AAB-T.2.2.9 MONTAJUL ȘI EXPLOATAREA |
AAB-T.2.2.1
DEFINIRE
Asamblarea prin strângere pe cilindru
(brățară) este asamblarea de tip arbore-butuc, demontabilă,
care transmite sarcinile prin frecarea care ia naștere pe suprafața
cilindrică de contact dintre arbore și o brățară apăsată cu ajutorul unor
asamblări cu șuruburi (fig.
AAB-T.2.2.1.1).
AAB-T.2.2.2 STRUCTURA CONSTRUCTIVĂ
|
|
|
|
a |
b |
|
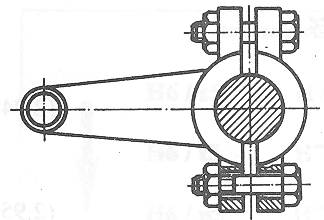
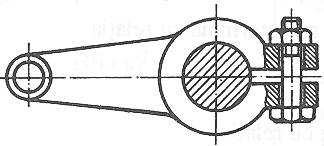
Fig. AAB-T.2.2.2.1 Asamblări
cu strângere pe cilindru (brățară): a
cu brățară din două bucăți; b
cu brățară secționată |
|
AAB-T.2.2.3 DOMENII DE UTILIZARE, AVANTAJE ȘI
DEZAVANTAJE
Domenii principale de utilizare:
construcția de mașini pentru fixarea diferitelor manivele, brațe, suporți pe
bare, tije, coloane, osii sau arbori; fixarea levierelor de acționare sau de
comandă
Tab.
AAB-T.2.2.3.1 Avantaje și dezavantaje ale asamblărilor prin
strângere ce cilindru
|
Avantaje* |
Dezavantaje* |
|
-
se pot face
poziționări axiale și unghiulare diferite; |
-
sarcini relativ
reduse; -
se impune
reglarea strângerii; -
inadecvate în
cazul montărilor și demontărilor frecvente |
AAB-T.2.2.4 CLASIFICARE
Tab.
AAB-T.2.2.4.1 Clasificarea asamblărilor prin strângere pe
cilindru (brățară)
|
Criteriul |
Tipul asamblării |
Schema |
|
Forma brățării |
Cu brățară din două bucăți |
Fig. |
|
Cu brățară secționată |
Fig. |
|
|
Asamblarea cu filet |
Cu piuliță |
|
|
Cu filet în corpul brățării |
|
AAB-T.2.1.5 MATERIALE ȘI TEHNOLOGII
Brățările
se execută din oțel laminat sau din tablă, recomandându-se ca rugozitatea
suprafețelor de contact să fie cât mai mare
AAB-T.2.1.6 FORME ȘI CAUZE DE SCOATERE
DIN UZ SAU DE COMPORTARE NECORESPUNZĂTORE
Tab.
AAB-T.2.1.6.1 Forme și cauze de scoatere din uz sau de comportare
necorespunzătoare
|
Forme |
Consecințe |
Apariție |
Cauze |
Manifestare |
Evitare |
|
Deteriorarea
suprafeței de contact (deformare
plastică) |
Întreruperea
transmiterii sarcinii |
La
arborii și brățări din materiale moi puternic încărcate |
Depășirea tensiunilor de strivire ale materialelor |
Deteriorarea suprafețelor active
de contact ale arborelui și/sau brățării |
Limitarea prin calcul a tensiunilor de strivire la valori
admisibile |
|
Deteriorarea
asamblării filetate |
Micșorarea
jocurilor din elementele adiacente (rulmenți,
lagăre cu alunecare) |
La
asamblările elementelor de rezemare |
Depășirea deformațiilor radiale admisibile |
Comprimarea arborelui și/sau extensia radială a butucului |
Limitarea prin calcul a deformațiilor radiale |
AAB-T.2.1.7 PARAMETRI FUNCȚIONALI ȘI
CONSTRUCTIVI
AAB-T.2.1.8 MODELE DE CALCUL
|
|
Ipoteze
de calcul și solicitări:
-
sarcina exterioară se transmite integral prin frecare; -
presiunile pe
suprafețele de contact sunt uniform distribuite; - șuruburile de strângere a brățărilor sunt încărcate identic și sunt solicitate la tracțiune. Condiţia de rezistenţă la torsiune a arborelui în zona asamblării Diametrul minim al arborelui în zona asamblării, din condiţia de rezistenţă la solicitarea de torsiune,
trebuie să respecte relaţia, d ≥
unde, τat = 15...45 MPa este tensiunea admisibilă la torsiune convenţională (ţine cont şi de existenţa solicitării de încovoiere, se iau valori maxime când încovoierea este redusă sau chiar nulă (la cap de arbore); materialul este oțel) şi βk = 1...2, factorul concentratorului de tensiuni (pentru calculul la oboseală). Condiția de transmitere sarcinii prin frecare, se determină din ecuația de echilibru a momentelor,
” N d
≥ βa Mt
,
(AAB-T.2.1.8.1.3) în care, Mt [Nmm] este
momentul de torsiune transmis, d [mm] diametrul arborelui, ” -
coeficientul de frecare (pentru cazul pieselor din oțel ” = 0,15
0,2), N [N] - forța normală de apăsare a brățărilor;
βa
=
1,2
1,8 factor de siguranță la alunecare (patinare). Din ecuația de echilibru a
forțelor ce acționează asupra unei brățări (varianta din fig.
AAB-T.2.1.8.,a) sau a unei semibrățări articulată
în punctul A (varianta din fig. AAB-T.2.1.8.1,b), se obține, N = z Faș sau, respectiv, N a = z Faș b,
(AAB-T.2.1.8.1.4) unde, z este numărul de șuruburi de strângere a brățărilor; a și b - lungimi adoptate constructiv. Condiția de
rezistență la strivire a asamblării, ținând cont de relația
(AAB-T.2.1.8.1.3) este,
unde, l este lungimea brățărilor, σas
= min(σas a, σas b) tensiunea admisibilă
la strivire (σas a,b
tensiunile admisibile de strivire ale materialelor arborelui și, respectiv,
brățării). Calculul
asamblării cu șuruburi Din relația
(AAB-T.2.1.8.1.3), ținând cont de relația (AAB-T.2.1.8.1.4), rezultă forța axială
de strângere a unui șurub,
pentru asamblarea cu brățara
din două bucăți sau, respectiv, pentru cea cu brățară articulată; valoarile
obținute cu aceaste relații se utilizează pentru calculul asamblării cu un
șurub solicitată axial. |
|
a |
|
|
|
|
|
b |
|
|
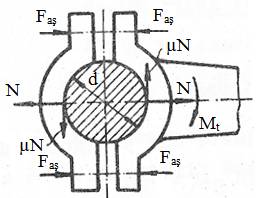
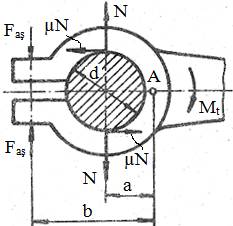
Fig.
AAB-T.2.1.8.1 Schema de calcul a asamblării cu strângere pe
cilindru: a cu brățară din două bucăți:
b cu brățară secționată |
AAB-T.2.1.9 MONTAJUL ȘI EXPLOATAREA