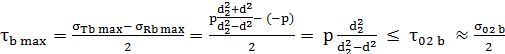AAB. ASAMBLĂRI ARBORE-BUTUC

AAB-T. CONSTRUCŢIA ŞI MODELAREA ASAMBLĂRILOR ARBORE-BUTUC

AAB-T.2 ASAMBLĂRI PRIN FRECARE

AAB-T.2.1 ASAMBLĂRI CU STÂNGERE PROPRIE (PRESATE)

CUPRINS

AAB-T.2.1.1 DEFINIRE

AAB-T.2.1.2 STRUCTURA CONSTRUCTIVĂ

AAB-T.2.1.3 DOMENII DE UTILIZARE, AVANTAJE ŞI DEZAVANTAJE

AAB-T.2.1.4 CLASIFICARE

AAB-T.2.1.5 MATERIALE ŞI TEHNOLOGII

AAB-T.2.1.6 FORME ŞI CAUZE DE SCOATERE DIN UZ SAU DE COMPORTARE NECORESPUNZĂTORE

AAB-T.2.1.7 PARAMETRII FUNCŢIONALI ŞI CONSTRUCTIVI

AAB-T.2.1.8 MODELE DE CALCUL

AAB-T.2.1.8.1 Modele de calcul a încărcărilor

AAB-T.2.1.8.2 Model de calcul a strângerilor (deformaţiilor) radiale elastice necesare

AAB-T.2.1.8.3 Model de calcul de rezistenţă a asamblărilor cu strângere proprie presate sau fretate

AAB-T.2.1.8.4 Model de calcul la deformaţii a asamblărilor cu strângere proprie presate sau fretate

AAB-T.2.1.8.5 Model de calcul termic a asamblărilor cilindrice cu strângere proprie fretate

AAB-T.2.1.9 MONTAJUL ŞI EXPLOATAREA

AAB-T.2.1.1 DEFINIRE

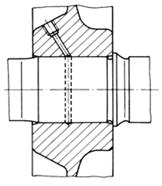
Asamblarea prin strângere proprie (presată) este legătura de tip arbore-butuc, nedemontabilă sau, rareori, demontabilă, care transmite sarcinile prin frecarea care ia naştere pe suprafaţa de contact dintre arbore şi butuc sub acţiunea presiunilor de contact care apar după montaj datorită strângerii reciproce generată de deformaţiile elastice (fig. AAB-T.2.1.1.1).

AAB-T.2.1.2 STRUCTURA CONSTRUCTIVĂ

a	b
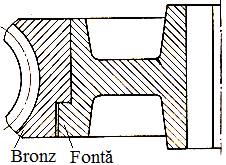
Fig. AAB-T.2.1.2.1 Asamblări cu strângere proprie directe (fără elemente intermediare): a – nedemontabilă (pentru elemente din materiale diferite, ex. coroană melcată pe butuc); b – demontabilă (pentru solidarizarea unor elemente şi/sau subansamble diferite)

AAB-T.2.1.3 DOMENII DE UTILIZARE, AVANTAJE ŞI DEZAVANTAJE

Domenii principale de utilizare: montare volanţi, bucşe de lăgăruire în carcase; bandaje montate pe roţi de vehicule de cale ferată; arbori cotiţi asamblaţi prin presare; îmbinarea unor elemente ale zalelor de lanţ; asamblarea coroanelor dinţate pe corpul roţii; asamblarea rulmenţilor pe fusurile arborilor.

Tab. ACA-T.3.1 Avantaje şi dezavantaje ale asamblărilor prin strângere proprie

Avantaje^*	Dezavantaje^*
- capacitate de transmitere a sarcinilor mari; - comportare bună la sarcini variabile; - centrare bună a pieselor asamblate; - fac posibilă execuţia pieselor din mai multe părţi în scopul economisirii materialelor scumpe şi/sau deficitare sau pentru uşurarea tehnologiei de fabricaţie	- precizia de execuţie ridicată a elementelor active, impusă de condiţiile de funcționare şi de montaj; - deteriorarea suprafeţelor funcţionale, la demontări şi montări repetate; - necesitatea sortării pieselor pentru asigurarea riguroasă a strângerilor impuse

AAB-T.2.1.4 CLASIFICARE

Tab. AAB-T.2.1.4.1 Clasificarea asamblărilor prin strângere proprie [Horovitz, 1969; Jula, 1986; Rădulescu, 1981]

Criteriul	Tipul asamblării
Soluţia constructivă	Fără elemente de strângere
	Cu elemente de strângere
Posibilitatea de demontare	Demontabile
	Nedemontabile
Tehnologia de asamblare	Presate (introducerea forţată axial a arborelui în butuc, de obicei, la temperatura mediului ambiant)
	Fretate (încălzirea butucului sau/şi răcirea arborelui în scopul obţinerii de strângeri mai mari decât în cazul celor presate la rece)
Obs. Caracterul demontabil sau nedemontabil este determinat de mărimea strângerii şi de tehnologia de montaj folosită

AAB-T.2.1.5 MATERIALE ŞI TEHNOLOGII

În cazul asamblărilor cu strângere proprie pe suprafeţe cilindrice, presate sau fretate, nu există un element intermediar între elementele asamblate (arbore şi butuc), pentru calcul se iau în considerare materialele celor două elemente.

Operaţia de presare la rece sau la cald se execută cu prese manuale (strângeri mici) sau hidraulice (strângeri mari); pentru micşorarea forţei axiale de presare se pot unge suprafeţele de contact (capacitatea de transmitere a sarcinii scade).

Operaţia de fretare presupune încălzirea butucului (la flacără deschisă, în cuptor sau în baie de ulei), de obicei, sub 600^oC sau/şi răcirea arborelui (în oxigen lichid sau bioxid de carbon) în scopul micşorării sau chiar reducerii la valoare nulă a forţei axiale de montaj.

AAB-T.2.1.6 FORME ŞI CAUZE DE SCOATERE DIN UZ SAU DE COMPORTARE NECORESPUNZĂTORE

Tab. AAB-T.2.1.6.1 Forme şi cauze de scoatere din uz sau de comportare necorespunzătoare

Forme	Consecinţe	Apariţie	Cauze	Manifestare	Evitare
Deteriorarea suprafeţei de contact a arborelui sau butucului  (deformare plastică)	Blocarea asamblării şi împiedicarea demontării	La arborii şi butucii din materiale moi puternic încărcate	Depăşirea tensiunilor de strivire ale materialelor	Deteriorarea suprafeţelor active de contact ale arborelui şi/sau butucului	Limitarea prin calcul a tensiunilor de strivire la valori admisibile
Deformaţii elastice radiale mărite	Micşorarea jocurilor din elementele adiacente (rulmenţi, lagăre cu alunecare)	La asamblările elementelor de rezemare	Depăşirea deformaţiilor radiale admisibile	Comprimarea arborelui şi/sau extensia radială a butucului	Limitarea prin calcul a deformaţiilor radiale

AAB-T.2.1.7 PARAMETRI FUNCŢIONALI ŞI CONSTRUCTIVI

AAB-T.2.1.8 MODELE DE CALCUL

AAB-T.2.1.8.1 Modele de calcul a încărcărilor

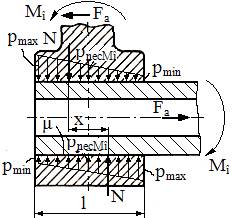
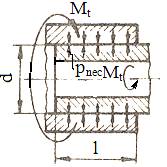
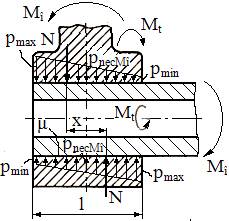
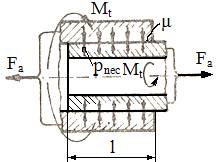
Tab. AAB-T.2.1.8.1.1 Situaţii de încărcare şi condiţiile asociate de transmitere a sarcinilor prin frecare

Cazul	Tipul sarcinilor	Schema de încărcare	Condiţia de transmitere a sarcinii prin frecare	Cazul	Tipul sarcinilor	Schema de încărcare (v. Obs. 1)	Condiţii de transmitere a sarcinii prin frecare şi formă (v. Obs. 1)
1	Forţă axială		sau	4	Moment de încovoiere şi forţă axială		, Mî sau = max(
2	Moment de torsiune		Mt  ≤ µ πdl  pnec sau pnec  ≥	5	Moment de încovoiere şi moment de torsiune		, Mî sau = max( .
3	Forţă axială şi moment de torsiune		sau	6	Moment de încovoiere, forţă axială şi moment de torsiune		, Mî , sau = max( .
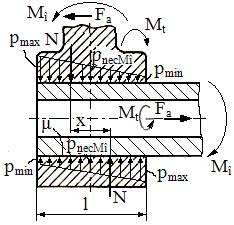
Obs.	a. În cazurile 1, 2 şi 3, datorită încărcărilor axiale, distribuţia presiunilor pe suprafaţa de contact este uniformă; transmiterea sarcinilor externe se face integral prin frecare. b. În cazurile 3,4,5, datorită încărcării cu momentul de încovoiere, distribuţia presiunilor pe suprafaţa de contact este neuniformă, cu presiunea medie pnec Mî = (pmin+ pmax)/2 Pentru calcul se poate considera cazul limită pmin =0 (pnec Mî = pmax/2), când acţiunea momentului de încovoiere în plan diametral se echivalează cu un cuplu prin relaţia, Mî = N x = dl pnec Mî x = dl pnec Mî l/3 = dl pmax/2 l/3 = dl^2 pmax l/6, în care s-a considerat x=l/3 şi, considerând distribuţia presiunii în plan frontal constantă, forţa N = dl pnec Mî. Deoarece, în aceste cazuri transmiterea momentului de torsiune se face prin formă şi sarcinile axiale prin frecare condiţiile de transmitere a sarcinilor axiale sunt independente şi, în consecinţă, pentru calcul se impune adoptarea valorilor maxime corespunzătoare celor două situaţii (cazurile 1,2 şi 3 sunt situaţii particulare ale cazurilor 4, 5 şi respectiv 6 pentru care se consideră, Mi = 0).

AAB-T.2.1.8.2 Model de calcul a strângerilor (deformaţiilor) radiale elastice necesare

	Ipoteze de calcul: - materialele arborelui şi butucului se deformează în domeniul elastic; - presiunea de contact pe suprafaţa comună se consideră constantă, uniform distribuită; - sarcinile exterioare se transmit prin forţele de frecare care apar pe suprafeţele de contact datorită strângerii. 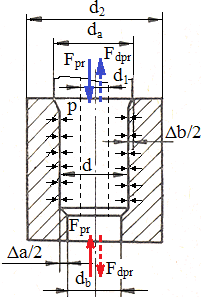Calculul strângerilor Strângerea teoretică necesară (conform teoriei elasticităţii tuburilor groase, relaţia lui Lame): (AAB-T.2.1.8.2.1) în care: p [MPa] reprezintă presiunea dintre suprafeţele în contact, p = pnec; d [mm] – diametrul suprafeţei de contact; da şi db diametrele iniţiale ale arborelui şi, respectiv butucului; Δa şi Δb deformaţia radială a arborelui (lărgire) şi respectiv, butucului (contracţe); Ea [MPa] şi Eb [MPa] - modulele de elasticitate ale materialelor arborelui şi, respectiv, butucului; arborelui şi, respectiv, butucului; ka şi kb -coeficienţi definiţi de relaţiile: ,  în care, νa şi νb reprezintă coeficienţii contracţiei transversale (Poisson) Strângerea corectată necesară, ia în considerare condiţiile reale de execuţie şi de montaj, conform relaţiei, Sc = S + Sn+ St în care: Sn reprezintă corecţia datorită microneregularităţilor de 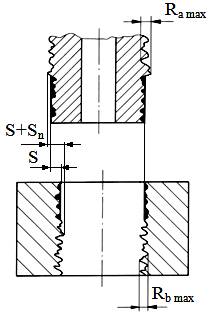prelucrare ale suprafeţelor care vin în contact conform expresiei, Sn = 1,2 (Ra max + Rb max) [μm], cu Ra,b max înălţimile maxime ale neregularităţilor, existente, iniţial, pe suprafaţa arborelui, respectiv a butucului (v. fer. ASP-P.1); St – corecţia efectului dilataţiilor termice ale pieselor asamblate în funcţionare, conform relaţiei St = [αb (tb – t0)- αa (ta – t0)] d .10^3 [μm], unde αa,b sunt coeficienţii de dilataţie termică ai materialului arborelui, respectiv, butucului; t0 – temperatura mediului ambiant la care s-a realizat montarea; ta,b – temperaturile de funcţionare a arborelui, respectiv, butucului, în ^oC. Forţele axiale necesare pentru presare sau la depresare, se determină cu relaţiile, Fpr = µ1 πdl p sau, respectiv,   Fdpr = µ2 πdl p, în care, µ1  reprezintă coeficientul de frecare la presare; µ2 - coeficientul de frecare la depresare (µ2 > µ1); pentru micşorarea forţei de presare se poate unge cu ulei suprafeţele de contact. Obs. Pentru calcule de proiectare se poate considera p = pnec, corespunzător schemei de încărcare (subcap. AAB-T.2.1.8.1)
a
b
Fig. AAB-T.2.1.8.1.2.1 Scheme de calcul a deformaţiilor: a – parametri geometrici; b - influenţa neregularităţilor suprafeţelor asupra strângerii [Roloff, 2008]

AAB-T.2.1.8.3 Model de calcul de rezistenţă a asamblărilor cu strângere proprie presate sau fretate [Jula, 1986; Rădulescu, 1981; Catrina, 2009]

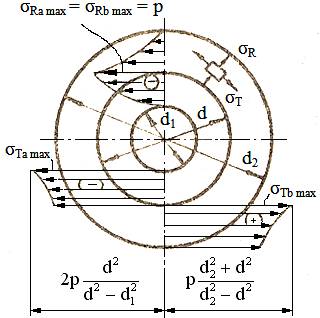
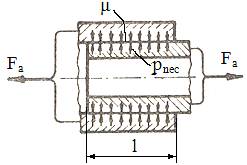
Fig. AAB-T.2.1.8.1.3.1 Schema de calcul a tensiunilor

Ipoteze simplificatoare: - tensiunile din piesele asamblate determinate de presiunile de contact se calculează pe baza relaţiilor stabilite în studiul tuburilor cu pereţi groşi în domeniul elastic; - în arbore şi butuc apar tensiuni radiale, σR, cu valori nule la interiorul arborelui şi exteriorul butucului şi tensiuni tangenţiale, σT, de tracţiune în butuc şi de compresiune în arbore; - pentru ca piesele asamblate să nu se deformeze plastic se impune conform teoriei tensiunilor tangenţiale îndeplinirea condiţiei, , (AAB-T.2.1.8.3.1) Condiţiile de evitare a deformaţiilor plastice (asigurare a strângerii elastice), pentru arbore şi butuc se determină cu relaţiile, , (AAB-T.2.1.8.3.2) şi respectiv, , (AAB-T.2.1.8.3.3) în care, σTa,b şi σRa,b sunt tensiunile tangenţiale şi, respectiv, radiale din arbore şi, respectiv, butuc; τ02 a,b şi σ02 a,b – limitele de curgere ale materialelor arborelui, respectiv butucului (în cazul materiale casante, de ex. fonta) se iau în considerare limitele de rupere τr şi σr). Valorile maxime (critice, admise la limită) pe care le pot atinge presiunile de contact, la limitele de curgere ale materialelor arborelui şi butucului (σ02a şi respectiv, σ02b), se pot stabili din relaţiile (AAB-T.2.1.8.3.2 şi AAB-T.2.1.8.3.3): şi, respectiv, (AAB-T.2.1.8.3.4) .

AAB-T.2.1.8.4 Model de calcul la deformaţii a asamblărilor cu strângere proprie presate sau fretate [Jula, 1986; Rădulescu, 1981; Catrina, 2009]

Ipoteze simplificatoare:

- materialele arborelui şi butucului se deformează în domeniul elastic;

- presiunea de contact pe suprafaţa comună se consideră constantă;

- deformaţiile elastice diametrale Δd_1,2 ale pieselor (arbore şi butuc) asamblate la nivelul diametrelor d_1,2 se calculează din relaţia lui Hooke,

şi . (AAB-T.2.1.8.4.1)

Condiţiile de evitare a deplasărilor radiale limită

Deplasările elastice diametrale , conform relaţiei lui Hooke din teoria elasticităţii, de micşorare a diametrului arborelui d₁ şi de mărire a diametrului butucului d₂ sunt:

[μm] şi, respectiv, [μm] (AAB-T.2.1.8.4.2)

AAB-T.2.1.8.5 Model de calcul termic a asamblărilor cilindrice cu strângere proprie fretate [Jula, 1986; Rădulescu, 1981; Catrina, 2009]

Obs. În cazul asamblării fretate din ecuaţiile de dilatare termică în direcţie diametrală a arborelui sau butucului,

şi respectiv, (AAB-T.2.1.8.1.5.1)

se obţin temperaturile de răcire a arborelui sau de încălzire a butucului,

[^oC] şi/sau respectiv, [^oC] (AAB-T.2.1.8.5.2)

unde, t₀ [^oC] este temperatura mediului ambiant de montaj; S_max [μm] – strângerea maximă de realizat conform ajustajului adoptat; α_a,b [1/ ^oC] – coeficienţii de dilatare termică unidirecţională ai materialelor arborelui, respectiv butucului; j_m [μm] – jocul suplimentar de montaj necesar pentru uşurinţa montajului.

AAB-T.2.1.9 MONTAJUL ŞI EXPLOATAREA
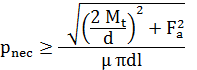
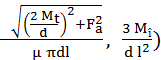
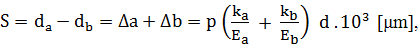
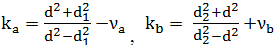