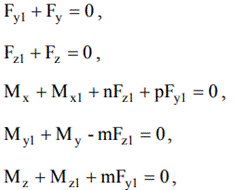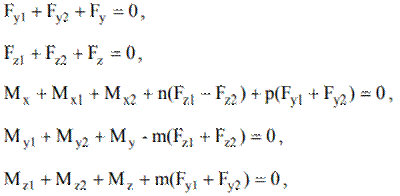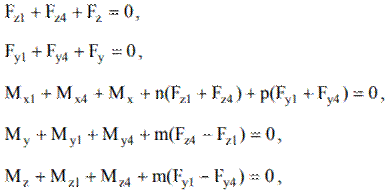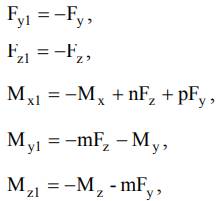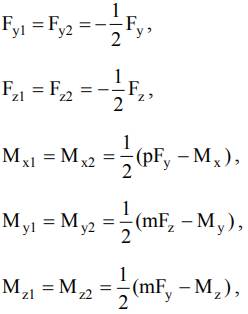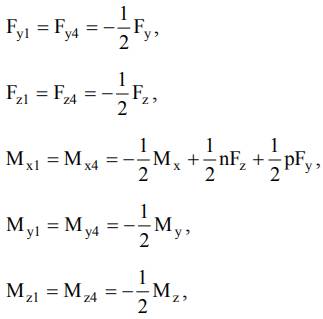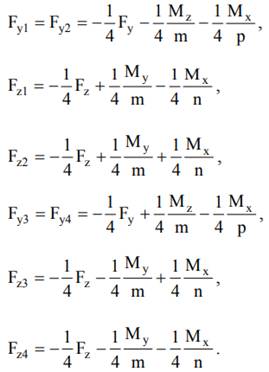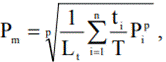|
Buzdugan I.D.,
Mogan Gh.L. Proiectarea roboților. Universitatea Transilvania din Brașov |
||||||||||||||||||||||
|
Subcap.T.7.2 Alegerea și verificarea
ghidajului |
||||||||||||||||||||||
|
Modele de încărcare a ghidajelor Model de încărcare a ghidajelor cu două coloane și patru bucși de ghidare cu rostogolire
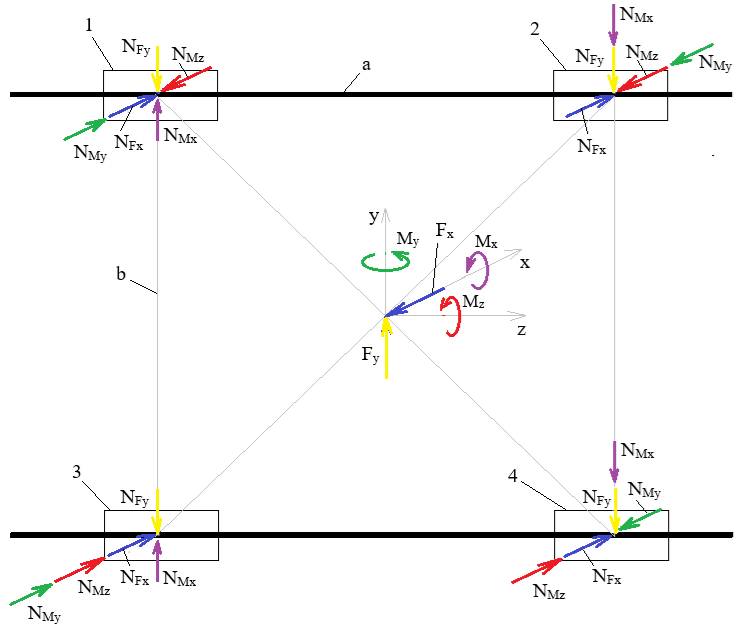
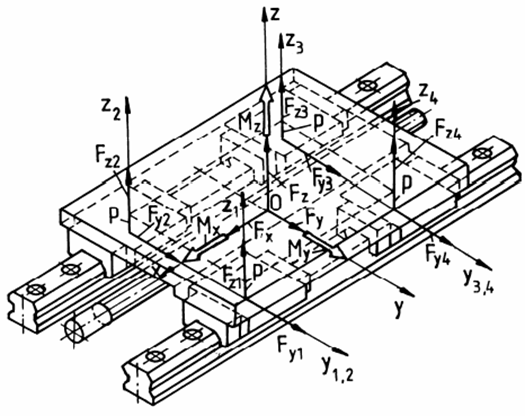
Fig. 1 Model de încărcare a bucșilor de ghidare Torsorul forțelor de reacțiune în centrul cuplei de translație: [+Fy, - Fx, - Mx, + My, -Mz]; semnele și valorile forțelor de reacțiune se obțin în urma modelării în MATLAB. Obs. În cazurile în care forțele de reacțiune au alte sensuri ca cele din fig. 1 se va reface modelul ținând cont de sensurile indicale de MATLAB. Reducerea forțelor
de reacține din centrul
cuplei la nivelul fiecărei bucși de ghidare Ipoteză: având în vedere simetria și neglijând erorile de dispunere (în colțurile unui dreptunghi cu laturile a, b) a bucșelor de ghidare efectul forței/momentului de inerție al torsorului în fiecare bucșă va fi o forță radială în centrul bucșei; sensul se va personaliza pentru fiecare bucșă (fig. 1). Forța de reacțiune, Fx (marcată cu galben), se reduce la forța radială, NFx = Forța de reacțiune, Fy (marcată cu albastru), se reduce la forța radială, NFy = Momentul de reacțiune, Mx (marcat cu maro), din relația de echilibru, Mx
= 2NMx a, se reduce la forța radială, NMx = Momentul de reacțiune, My
(marcat cu verde), din relația de echilibru, My = 2NMy a, se reduce la forța radială, NMy =
Momentul de reacțiune, Mz
(marcat cu roșu),
din relația de echilibru,
Mz = 2NMz b, se reduce la forța radială, NMz = Determinarea forței
de încărcare radială rezultantă pentru fiecare bucșă de ghidare
Identificarea bucșei
celei mai încărcată Bucșa cea mai încărcată radial se va determina din relația, N = max(N1, N2, N3, N4); valoarea N se va utiliza la alegerea bucșei de ghidare. Model de încărcare a ghidajelor cu două rigle și
patru, două sau o unităte (subansamblu) de ghidare cu rostogolire Pentru identificarea
încărcărilor (forțelor și momentelor), care solicită fiecare subansamblu de ghidare se impune reducerea încărcărilor exterioare, forțe și momente,
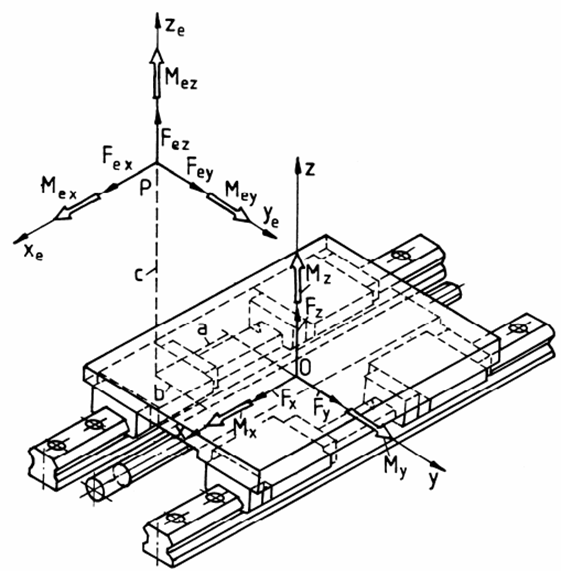
în centrul ghidajului (fig.2).
Fig. 2 Model de reducere a încărcărilor exterioare În cazul general, când încărcarea exterioară a ghidajului, sintetizată în torsorul [Fex Fey Fez Mex Mey Mez], se concentrează în punctul P de coordonate (a,b,c), componentele torsorului forțelor în centrul ghidajului (originea sistemului de coordonate asociat ghidajului; v. fig. 2.) sunt:
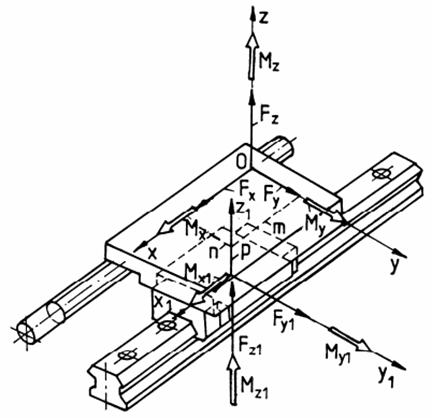
Schemele de calcul (încărcare) a ghidajelor, din punct de vedere constructiv, pot conține unul (fig.3), două (fig.4,a,b) sau patru (fig.5) subansamble specilizate de ghidare.
Fig. 3 Schema forțelor unui ghidaj cu un subansamblu de ghidare
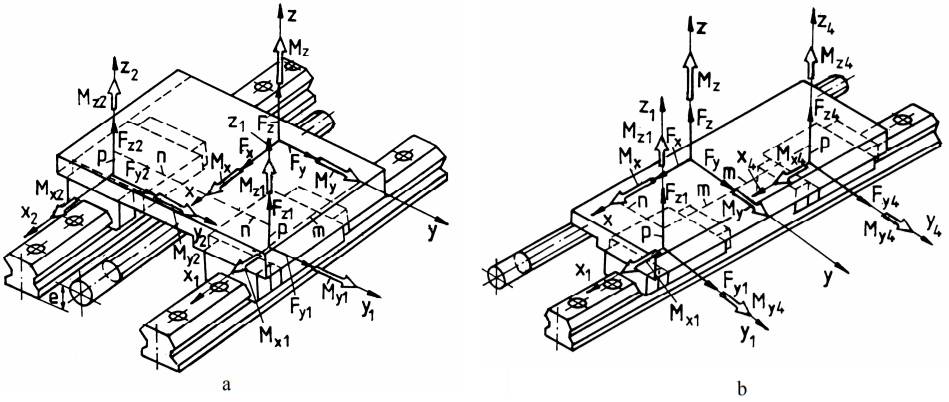
Fig. 4 Schema forțelor unui ghidaj cu două subansamble de ghidare Pentru identificarea încărcărilor subansamblelor de ghidare se asociază acestora câte un sistem de coordonate local cu axele paralele cu ale sistemului de coordonate asociat ghidajului, la distanțele m, n și p (fig.3, 4). Forțele și momentele care încarcă subansamblele de ghidare, pentru generalizare, se consideră în sensurile pozitive ale axelor locale. Pe de altă parte, se consideră construcția și montajele ghidajelor din modelele de calcul adoptate ca fiind ideale, fără abateri de execuție și de montaj. Ecuațiile de echilibru ale forțelor și momentelor, după axele asociate constrângeriilor induse de ghidaj sunt:
pentru ghidajul cu un subansamblu de ghidare (fig.3);
pentru ghidajul cu două subansamble de ghidare dispuse transversal (fig 4,a);
pentru ghidajul cu două subansamble de ghidare dispuse longitudinal (fig.4,b). Din sistemele formate din ecuațiile de echilibru ale forțelor de mai sus, rezultă expresiile forțelor de reacțiune din subansamblele de ghidare:
pentru ghidajul cu un subansamblu de ghidare (fig.3);
pentru ghidajul cu două subansamble de ghidare dispuse transversal (fig.4,a), considerându-se, în plus, și relațiile Fy1 = Fy2, Fz1 = Fz2, My1 = My2, Mz1 = Mz2, Mx1 = Mx2, rezultate din ipoteza simetriei de încărcare ideală;
pentru ghidajul cu două subansamble de ghidare dispuse longitudinal (fig.4,b), considerându-se, în plus, și relațiile Fy1 = Fy4, Fz1 = Fz4, My1 = My4, Mz1 = Mz4, Mx1 = Mx4, rezultate din ipoteza simetriei de încărcare ideală.
Fig. 5 Schema forțelor unui ghidaj cu patru subansamble de ghidare Pentru schema de calcul din fig. 5, din cauza gradului mărit de nedeterminare, se consideră că forțele torsorului de încărcare se împart egal pentru cele patru subansamble de ghidare (fiecărui subansamblu de ghidare îi revine câte o pătrime din forțele torsorului de încărcare) și astfel, aplicând suprapunerea de efecte, se obțin forțele de reacțiune:
Ghidajele cu rostogolire au frecări reduse și cvasiconstante la pornire și în timpul mișcării. Forțele de frecare din subansamblele de ghidare sunt dependente de tipul ghidajului, vâscozitatea lubrifiantului, sarcina aplicată, viteza de funcționare și precizia de montaj. Valorile medii ale forțelor de frecare se pot determina cu realția, Ff = μePm + F1, în care: μe este coeficientul de frecare de alunecare echivalent, Pm - forța normală la dirercția ghidajului, F1 - forța de rezistență internă (frecarea din etanșări, din căile de recirculare etc.) a subansamblului de ghidare. Valorile parametrilor μe, F1 sunt caracteristice fiecărui tip de subansamblu de ghidare și, de obicei, sunt indicate de producătorul acestora. Forme și cauze ale scoaterii din uz a subansamblelor de ghidare Principalele cauze ale scoaterii din uz a subansamblelor de ghidare, precum și formele de manifestare asociate, sunt prezentate în continuare. Oboseala straturilor superficiale ale căilor de rulare și ale corpurilor de rostogolire (pitting-ul) este cauza principală a scoaterii din uz a subansablelor de ghidare cu rostogolire ce funcționează la viteze mărite, unse abundent și bine etanșate. În aceste situații, în zonele de contact, după un număr mărit de contacte, apar microfisuri de oboseală, care consecință a presiunilor hidrostatice mărite din lubrifiant conduc la desprinderi de mici particule de material și deci la deteriorarea suprafețelor active și implicit la înrăutățirea funcționării (apariția de vibrații și zgomote). Evitarea acestei deteriorări și deci realizarea funcționării corespunzătoare într-o perioadă de timp impusă implică calculul de durabilitate a subansamblului de ghidare, ținând cont de capacitatea dinamică de încărcare. Deformarea plastică a suprafețelor active apare când subansamblele de ghidare sunt puternic solicitate, la viteze mult micșorate sau în repaus, și ungerea este insuficientă. Astfel, pe căile de rulare sau suprafețele corpurilor de rostogolire pot apărea mici amprente, datorită depășirii locale a limitei de curgere a materialului, consecință apariției unor presiuni de contact mult mărite. Evitarea acestei deteriorări, la subansamblele de ghidare, se face prin calculul static, care are la bază capacitatea statică de încărcare. Griparea apare în cazul subansamblelor de ghidare rapide, puternic încărcate și unse insuficient, sub forma unor zgârieturi pe căile de rulare și/sau pe suprafețele active ale corpurilor de rostogolire, consecință a unor microsuduri repetate în punctele de contact. Evitarea acestor deteriorări se realizează prin exploatarea și întreținerea corespunzătoare a subansamblului de ghidare. Uzarea abrazivă apare cu precădere datorită prezenței unor impurități în zonele active, consecință a ineficienței sistemului de etanșare, și se manifestă prin zgârieturi pe suprafețele active, ca urmare a așchierilor produse de aceste impurități. Distrugerea elementelor subansamblului prin rupere, de obicei accidentală, conduce la scoaterea din uz a acestuia. Există posibilitatea ruperii elementelor de poziționare (colivii) sau a celor de recirculare a corpurilor de rostogolire, consecință a apariției de uzări și jocuri mărite, ce conduc la posibilitatea blocării acestora. Calculul de durabilitate Durata de funcționre a unui subansamblu de ghidare se definește ca fiind lungimea totală de deplasare, exprimată în km, sau fiind timpul total de funcționare, în ore, realizat de ghidaj până la apariția primelor semne de oboseală a materialului, pe căile de rulare sau pe suprafețele active ale corpurilor de rostogolire. Durabilitatea de bază a unui subansamblu de ghidare este durata de funcționare atinsă de 90% din subansamblele unui lot, încercate independent, în aceleași condiții. Relația de calcul a durabilității, exprimată în km, este
în care lr este lungimea totală (în km) de deplasare de referință (50, pentru ghidajele cu bile sau 100 pentru cele cu role), C capacitatea (sarcina) dinamică de bază; Pm sarcina echivalentă (medie); p exponentul durabilității cu valoarea 3, pentru subansamblele de ghidare cu bile, sau 10/3, pentru cele cu role. Pentru cazurile când durabilitatea se exprimă în ore, se poate folosi relația,
în care: lc este lungimea cursei ghidajului exprimată în metri și n numărul de curse duble (dute-vino) realizate într-un minut. Capacitatea dinamică de bază este sarcina care solicită subansamblul de ghidare asigurând durabilitatea egală cu lungimea de referință. Valoarea acestui parametru, de obicei, se ia din cataloagele firmelor producătoare. Sarcina care solicită subansamblul de ghidare, de obicei, este variabilă de-a lungul cursei, fiind dependentă de forțele de reacțiune induse de subansamblul susținut, viteza și poziția acestuia în spațiu. Sarcina echivalentă (medie) este dată de încărcarea (forță sau moment), presupusă ca fiind constantă, care solicită subanasamblul de ghidare după una din direcțiile forțelor de reacțiune și conduce la aceeași durabilitate ca în cazul încărcării cu sarcină variabilă. Deoarece identificarea variației reale a încărcării este dificilă, echivalarea regimurilor de solicitare reale cu regimuri teoretice și mai departe acestea cu un regim echivalent cu încărcare constantă, se poate face prin intermediul unor modelele simplificate, prezentate în continuare. Modelul variației în trepte, aplicabil în cazul ghidajelor cu încărcări cvasiconstante pe lungimi de cursă diferite (fig. 5,a), presupune pentru calculul sarcinii echivalente, relația,
în care, unde T reprezintă timpul de deplasare pe cursa totală, ti - timpii de deplasare pe diversele tronsoane, Lt - lungimea totală de lucru, Pi încărcări parțiale corespunzătoare lungimilor Li ale tronsoanelor.
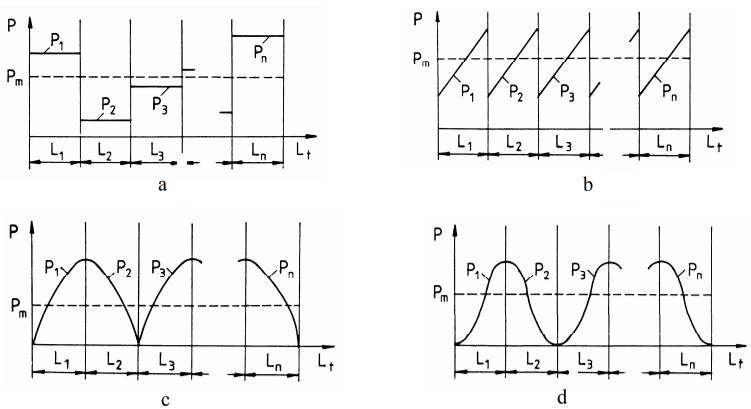
Fig. 5 Modele de echivalare a încărcării Modelul variației liniare în salturi (fig.5,b), aplicabil pentru situațiile când sarcina pe domeniul cursei de lucru este variabilă crescător, cu discontinuități bruște, conduce la sarcina echivalentă, dată de relația,
unde, Pmin = min(P1, Pn), Pmax = max(P1, Pn). Modelul variației sinusoidale consideră că încărcarea reală, aproximabilă cu arce de sinusoidă (fig.5,c), se echivalează cu sarcina Pm = 0,65Pmax, unde, Pmax = max(P1, Pn). Modelul variației parabolice ia în considerare aproximarea variației încărcării exterioare după o lege care are la bază arce de parabolă de ordinul doi, (fig.5,d), și face echivalența cu relația, Pm = 0,75Pmax, unde, Pmax = max(P1, Pn). Pentru calcule de verificare, durabilitatea de bază se multiplică cu factori de corecție dependenți de duritatea căilor de rulare, temperatura de lucru, direcția de orientare a încărcării exterioare etc., cuantificându-se astfel diferența dintre condițiile reale de funcționare și cele de testare în vederea determinării durabilității. Valorile acestor factori, de obicei, sunt indicate în cataloagele firmelor producătoare de subansamble de ghidare. Algoritmul de alegere și verificare a unui ghidaj Considerându-se ca date de intrare (lista de cerințe): sarcina exterioară, cursa maximă, durata de funcționare (în ore) sau distanța parcursă (în km), frecvența de deplasare, viteza maximă, accelerația maximă, precizia, rigiditatea, randamentul minim, masa admisibilă, gabaritul disponibil etc., algoritmul de alegere și verificare a unui ghidaj, folosind subansamble de ghidare specializate, poate avea următoarele etape: A. Adoptarea schemei ghidajului (v. fig.2, 3, 4) este o etapă complexă fără modele matematice la bază și presupune cunoașterea caracteristicilor și particularităților funcționale, constructive și de montaj ale ghidajelor din diverse aplicații practice Pentru cazul sistemelor mecanice ale produselor mecatronice, în special pentru roboții industriali, se adoptă variante care în cazul structurilor mecanice suspendate, în plus, asigură gabarite și mase micșorate. B. Determinarea torsorului forțelor de reacțiune care încarcă ghidajul, pornind de la încărcările exterioare, cu relațiile de mai sus, având la bază modelul din fig.1 sau rezultatele analizei dinamie cu MatLab. C. Determinarea încărcărilor subansamblelor de ghidare, pornind de la torsorul încărcării ghidajului, se face cu relațiile de mai sus pentru cazurile prezentate. În unele situații practice, având în vedere gradul de nedeterminare mărit, se întocmesc modele de analiză cu elemente finite pentru determinarea încărcărilor subansamblelor de ghidare. D. Alegerea subansamblelor de ghidare componente ale ghidajului adoptat, având în vedere multitudinea de soluții constructive oferite de firmele specializate, este de asemenea o etapă complexă, care presupune cunoașterea în detaliu a performanțelor și caracteristicilor diverselor subansamble de ghidare (v. exemplele prezentate în acest capitol), pe de-o parte și a specificităților produsului în care acestea sunt incluse, pe de altă parte. Pentru roboții industriali urmărind caracteristicile impuse de produsele mecatronice, de obicei, se adoptă subansamble de ghidare cu bile pentru structurile suspendate (Anexa PT.3) și cu role pentru structurile de susținere (de bază) (Anexa PT.4). Subansamblele de ghidare cu role recirculabile se remarcă prin performanțe mărite de precizie, portanță, rigiditate, absența mișcărilor de stick-slip, frecare constantă la un nivel ridicat de invarianță cu viteza. Pornind de la tipul subansamblului de ghidare adoptat, ținând cont de ofertele diverșilor producători și de încărcările impuse, se alege mărimea și se identifică parametrii geometrici și caracteristicile. E. Verificarea subansamblelor de ghidare la durabilitate se face având la bază inecuația, Ld,h ≤ Ld,h imp , în care Ld,h sunt durabilitaea subansamblului de ghidare ales în km, respectiv în ore, calculată cu relațiile de mai sus; Ld,h imp durabilitatea impusă, de asemenea, în km, respectiv în ore. Pentru calculele de verificare, ținând cont de încărcările și condițiile de lucru reale, se fac corecții prin intermediul unor factori, de obicei, cu valorile indicate de producător în cataloage. De exemplu, pentru ghidajele cu bile de tip bucșă (Anexa PT.3) se corectează capacitatea dinamică de bază. F. Alegerea sistemului de pretensionare se face ținând cont de aplicație, de posibilitățile de acces, de tipurile subansamblelor de ghidare folosite etc. G. Adoptarea sistemelor de etanșare și protecție ținând cont de mediul și condițiile de lucru Linkuri https://www.youtube.com/watch?v=wsS7ifd-Gpo |
||||||||||||||||||||||