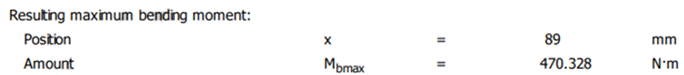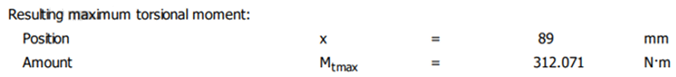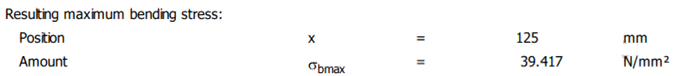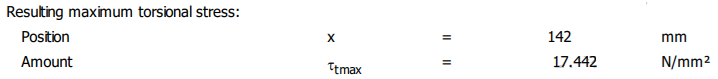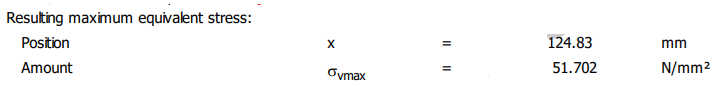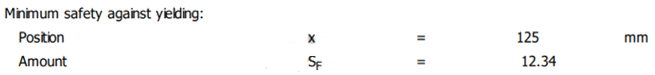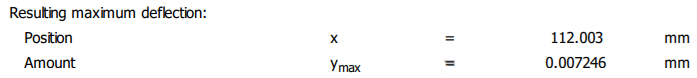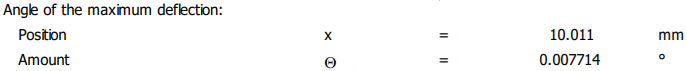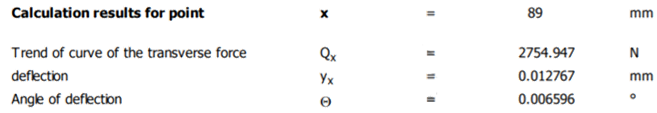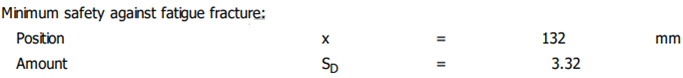|
…autori… Organe de Mașini. Lucrări de laborator. Universitatea Transilvania din Braşov |
||||||
|
Lucrarea LD.OM II.05 ANALIZA CU MDESIGN A SOLICITĂRILOR ARBORILOR DREPȚI
|
||||||
|
CUPRINS |
||||||
|
A. DESCRIEREA TEMATICII B. CLASIFICARE ȘI DESCRIERE C. MODELE DE CALCUL D. DATE DE INTRARE PENTRU ANALIZA CU MDESIGN E. REZULTATE ȘI VERIFICĂRI Obs. Acest document este o extensie a documentului Ghid.13.1.1 (Verificare arbori intermediari ai RConCil cu MDESIGN): https://rrv.unitbv.ro/RConCil/Ghiduri CATIA, MDESIGN/Ghid.13.1.1 Verificare arbore intermediar cu MDESIGN.htm, în care se prezintă explicații și comentarii suplimentare |
||||||
|
A. DESCRIEREA TEMATICII |
||||||
|
A.1 Aspecte generale |
||||||
|
Arborii drepţi sunt elemente de maşini cu mişcare de rotaţie destinate susţinerii altor elemente de maşini (roţi dinţate, roţi de curea, semicuplaje, volanţi etc.) şi transmiterii momentelor de torsiune, care, la rândul lor, se sprijină prin intermediul lagărelor (cu alunecare sau cu rostogolire) pe structuri, de obicei, fixe (şasiuri, batiuri, carcase etc.) |
||||||
|
A.2 Scopul lucrării |
||||||
|
Prin efectuarea lucrării de laborator se urmărește cunoașterea tipurilor arborilor, structurilor acestora, modelelor de analiză cu MDESIGN, rezultate și verificări |
||||||
|
B. CLASIFICARE ȘI DESCRIERE |
||||||
|
B.1 Clasificare și structură |
||||||
|
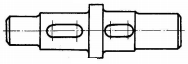
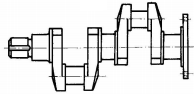
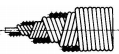
Tipuri de arbori ( fig. a – arbori drepţi; fig. b - arbori cotiţi; fig. c - arbori flexibili)
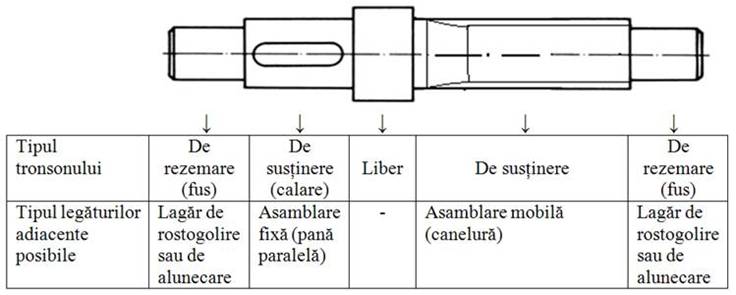
Structura constructivă generală a arborilor drepți
Forme constructive: |
||||||
|
B.2 Materiale și tratamente termice |
||||||
|
Materiale pentru arbori Pentru execuţia arborilor drepţi se utilizează frecvent, oţelurile: - de uz general pentru construcţii (E295, E335, E360), care nu necesită tratament termic, pentru cazuri de încărcare cu sarcini reduse; - carbon de calitate de îmbunătăţire (C 45, C55 etc.) şi aliate de îmbunătăţire (40 Cr 10, 41 CrNi 12 etc.), pentru cazuri de încărcare cu sarcini medii; - carbon de calitate de cementare (C 15, C 20 etc.) şi aliate de cementare (13 CrNi 30, 16MnCr5 etc.), pentru cazuri de încărcare cu sarcini mari. Fontele sunt utilizate pentru execuţia arborilor de dimensiuni mari deoarece sunt mai puţin sensibile la efectul concentratorilor de tensiuni şi amortizează mai bine vibraţiile.
Tratamentele termice ale arborilor din oțeluri Tratamentele termice și/sau termochimice aplicate arborilor drepți depind de materialul din care se execută arborii, pot fi: - îmbunătăţire sau îmbunătăţire şi călire superficială a fusurilor, canelurilor, porţiunilor de calare; - cementare urmată de călire a fusurilor, porţiunilor de calare şi a canelurilor; - nitrurare etc. |
||||||
|
B.3 Parametri funcţionali şi constructivi principali |
||||||
|
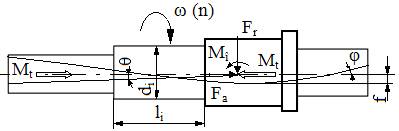
Schema parametrilor principali
Parametri cinematici ω [rad/s] – viteza unghiulară, n [rot/min]) – turaţia; relații de dependență: ω = π n/30, n=30 ω/π.
Parametri de încărcare Mt [Nmm] – momentul de torsiune transmis, Mî [Nmm] – momentul de încovoiere, Fr [N] – forţa radială, Fa [N] – forţa axială.
Parametri geometrici i = 1…n – numerele tronsoanelor; di , li [mm] – diametrul, lungimea tronsonului i.
Parametri de flexibilitate (rigiditate) f [mm] – săgeata la încovoiere, φ [grade] – rotirea la încovoiere, θ [grade] – rotirea la torsiune (răsucire) |
||||||
|
C. MODELE DE CALCUL |
||||||
|
C.1 Modele de încărcare a arborilor intermediari ai reductoarelor conico-cilindric |
||||||
|
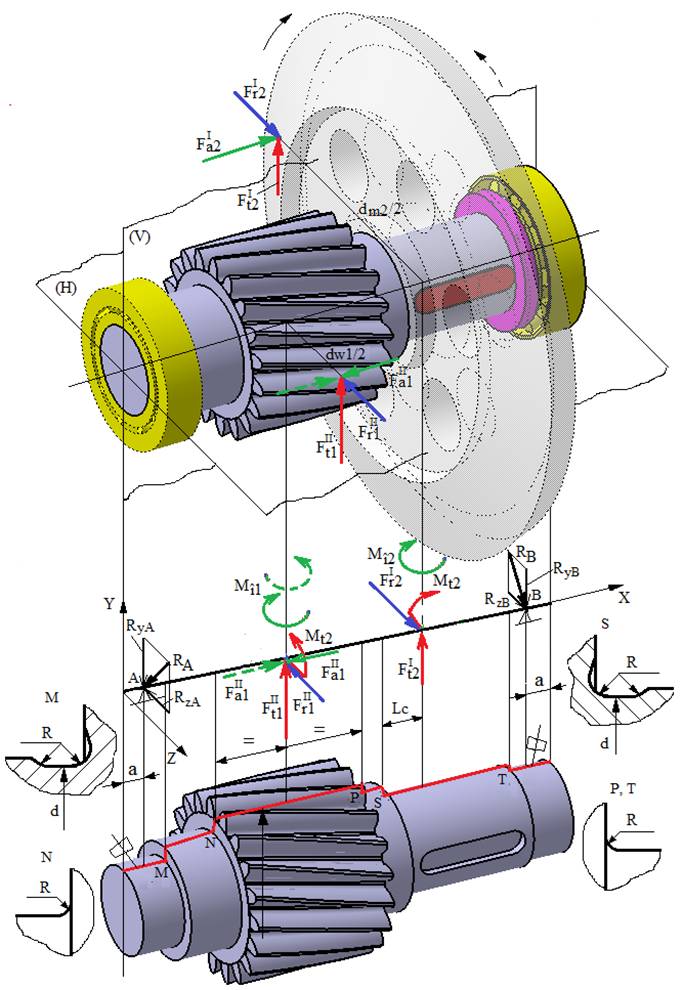
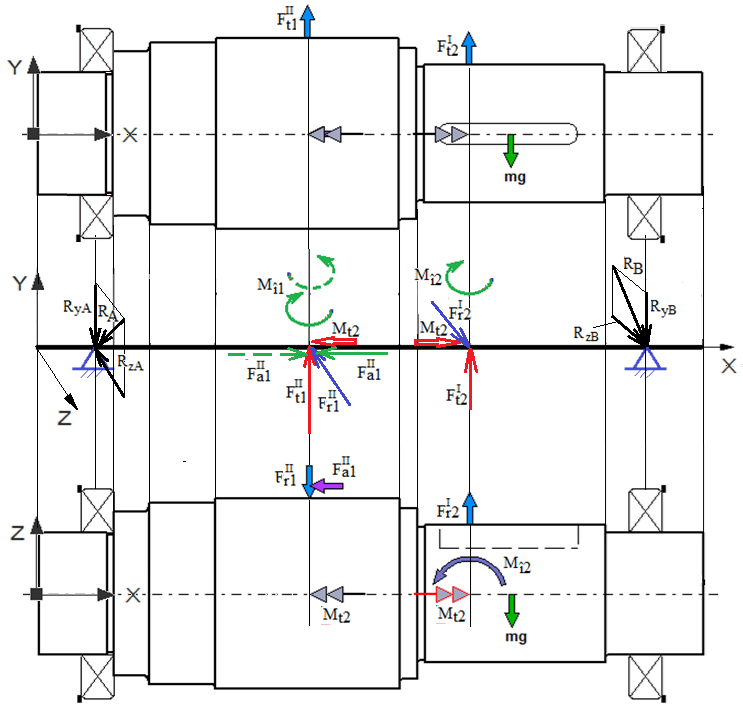
Model de încărcare a arborelui intermediar al unui RConCil HH
Semnificații parametrii: I – angrenaj conic, II – angrenaj cilindric, H – plan
orizontal, V – plan vertical, Valorile momentelor
de încovoiere: Mî1 = Obs. În continuare, se va prezenta analiza cu MDESIGN a arborelui intermediar al RConCil cu modelul de încărcare de mai sus; pentru celelalte tipuri de reductoare cilindrice analiza arborilor intermediari este similară. Alte modele de analiză cu MDESIGN a arborilor intermediari se pot urmări la adresa: |
||||||
|
C2. |
||||||
|
|
||||||
|
D. DATE DE INTRARE PENTRU ANALIZA CU MDESIGN |
||||||
|
D.1 Date despre geometrie |
||||||
|
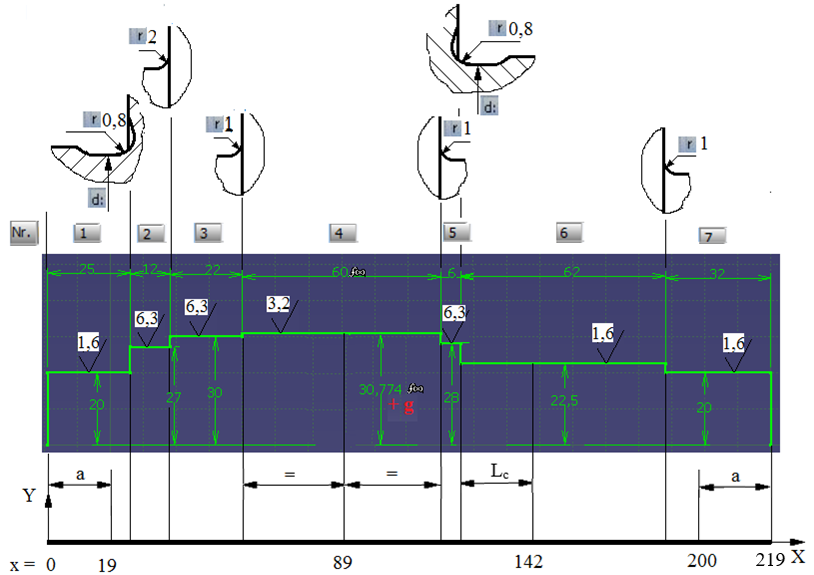
Generalități despre MDESIGN: Schema modelului geometric
Valori diametre şi lungimi Diametrele tronsoanelor: conform modelului CATIA (v. schema modelului geometric de mai sus). Lungimi de poziţionare a forţelor şi reacţiunilor (v. schema modelul de încărcare de mai sus): - Lc, distanţa de la conul suplimentar mediu al roţii conice, unde acţionează forţele din angrenaj (secţiunea mediană), la suprafaţa de rezemare a acesteia pe arbore (v. modelul de încărcare de mai sus); aceasta se determină prin măsurare din modelul 3D CATIA al roţii conice; - forțelor asociate pinionului cilindric se poziționează la mijlocul danturii acestuia; - a, din catalogul de rulmenţi corespunzătoare rulmentului adoptat; Valori forţe şi momente Momentul de torsiune, Mt2. Forţele
de încărcare a roţii conice: tangenţială, Forţele
de încărcare a pinionului cilindric: tangenţială, Momentele de încovoiere: - Mî2 = - Mî1 = pentru valorile diametrelor dm2 şi dw1 cunoscute. Turația arborelui n = n2, turaţia arborelui intermediar. Teșituri și racordări: https://rrv.unitbv.ro/RConCil/Anexe/Anexa.D04 Tesituri si racordari simple.htm Degajări pentru rectificare: https://rrv.unitbv.ro/RConCil/Anexe/Anexa.D06 Degajari pentru rectificare.htm |
||||||
|
D2. Date despre încărcări |
||||||
|
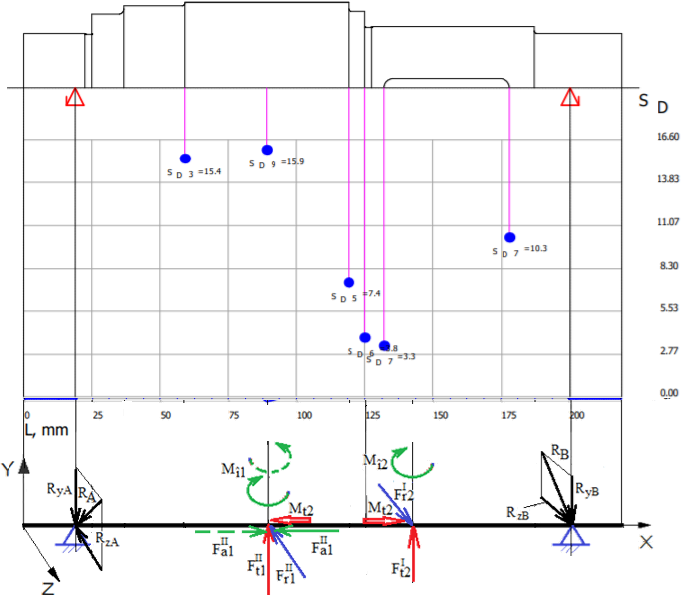
Model MDESIGN axonometric
Modele MDESIGN de încărcare în planele XY și ZX
|
||||||
|
D3. Date despre material, coeficienți de siguranță și caracteristici de calcul la oboseală |
||||||
|
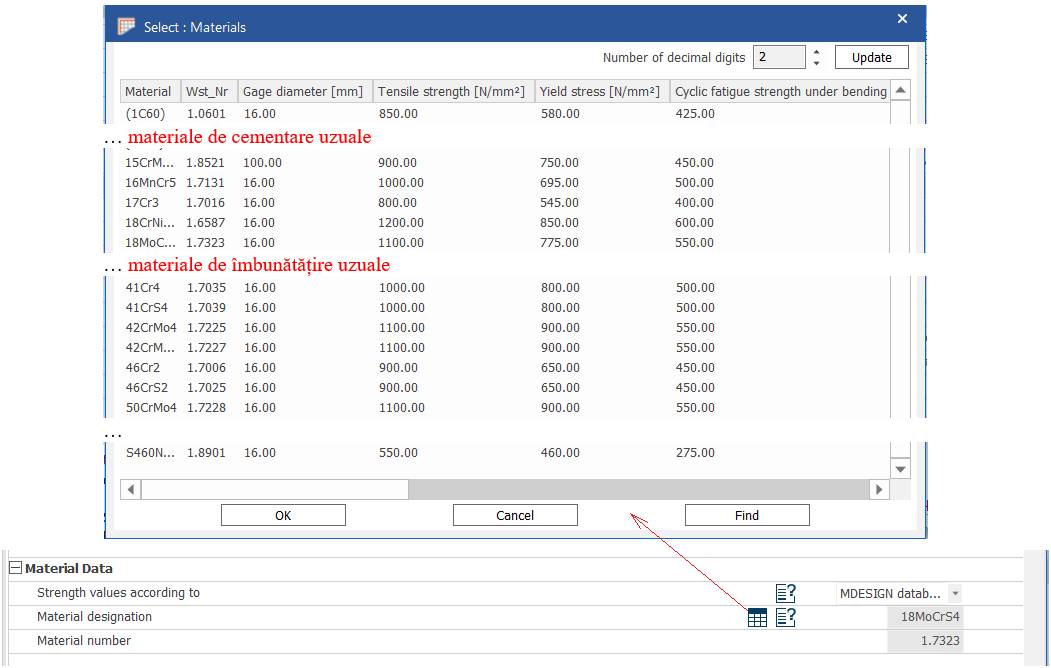
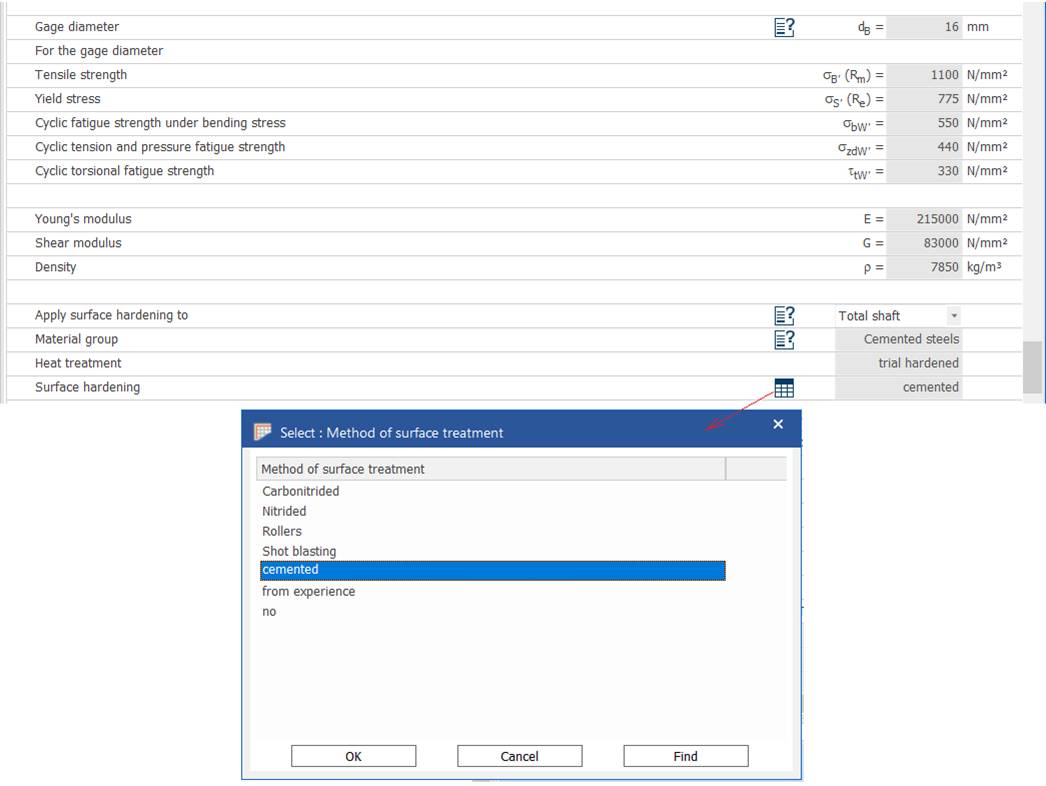
Alegerea materialului din baza de date MDESIGN
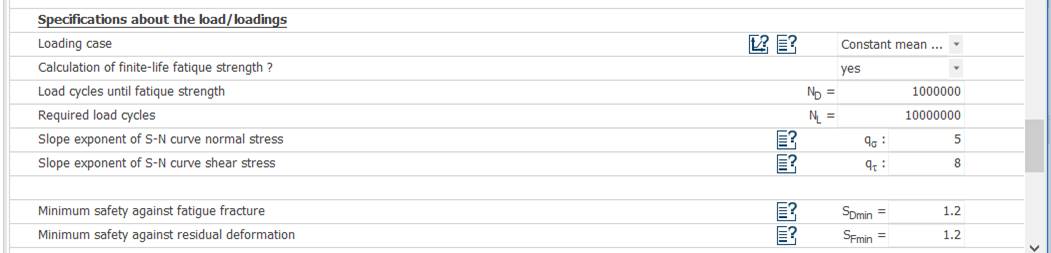
Date generale despre încărcări, calculul la oboseală și coeficienți de siguranță
|
||||||
|
E. REZULTATE ȘI VERIFICĂRI |
||||||
|
E.1 Date generale despre arbore |
||||||
|
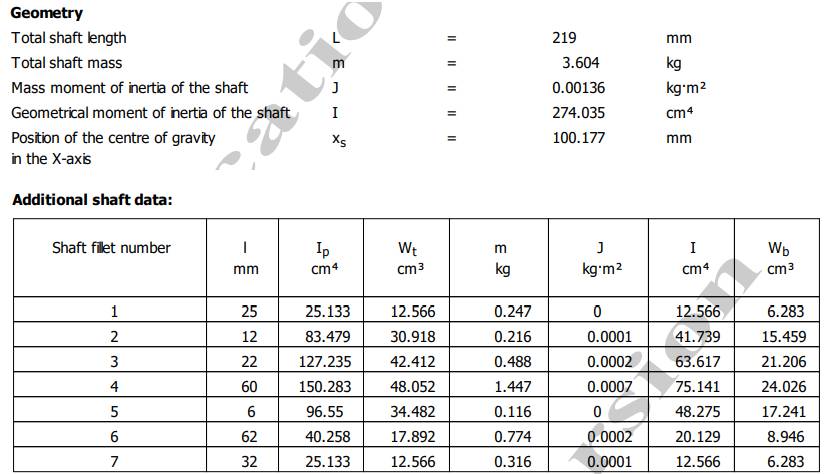
Valori parametri geometrici și inerțiali
Semnificații notații: L - Total shaft length (lungimea totală a arborelui); m – Total shaft mass (masa totală a arborelui; J – Mass moment of inertia of the shaft (momentul de inerție masic al arborelui), I – Geometrical moment of inertia of the shaft (momentul de inerție geometric); xs – Position of the centre of gravity in the X-axis (poziția centrului de greutate pe axa X), Ip – momentul de inerție polar, Wt – momentul static, Wt – modulul de rezistență axial |
||||||
|
E.2 Reacțiunile din lagărele cu rulmenți |
||||||
|
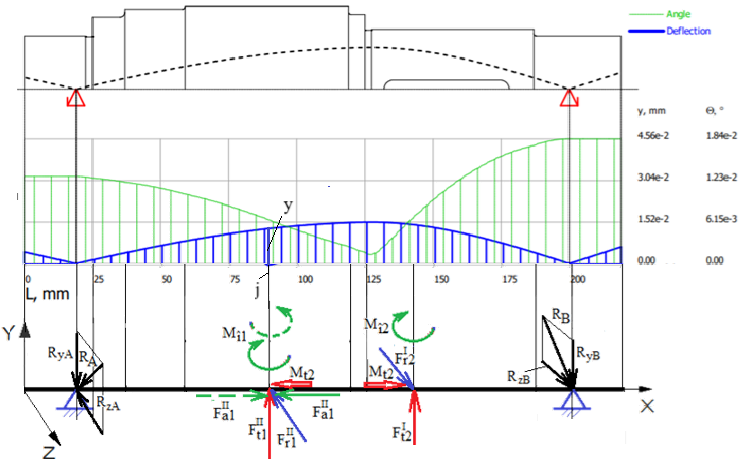
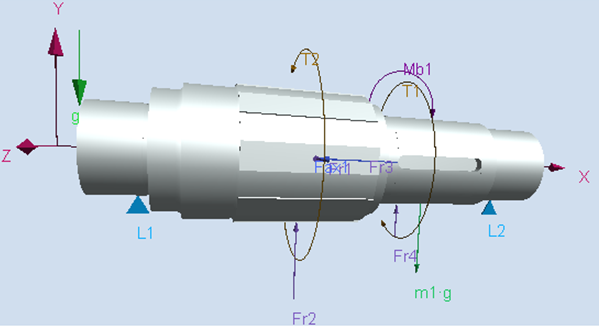
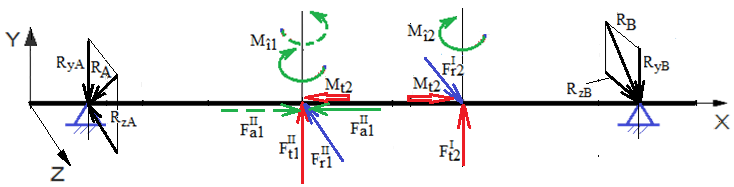
Schema de încărcare a arborelui cu marcarea forțelor de reacțiune din lagăre
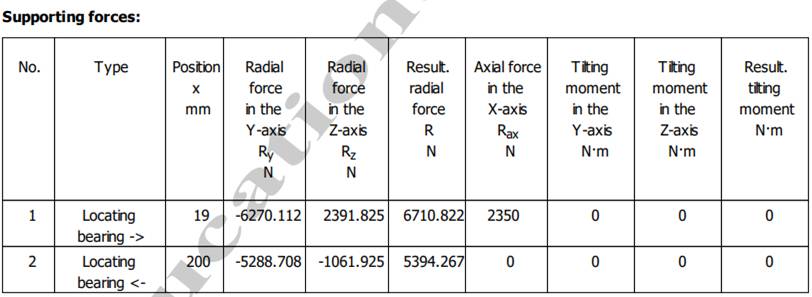
Valori ale forțelor de reacțiune din reazeme (lagăre cu rulmenți) Obs. Valorile forțelor reacțiunilor din lagăre din acest tabel vor fi folosite pentru calculul rulmenților: |
||||||
|
E.3 Verificarea la solicitări compuse |
||||||
|
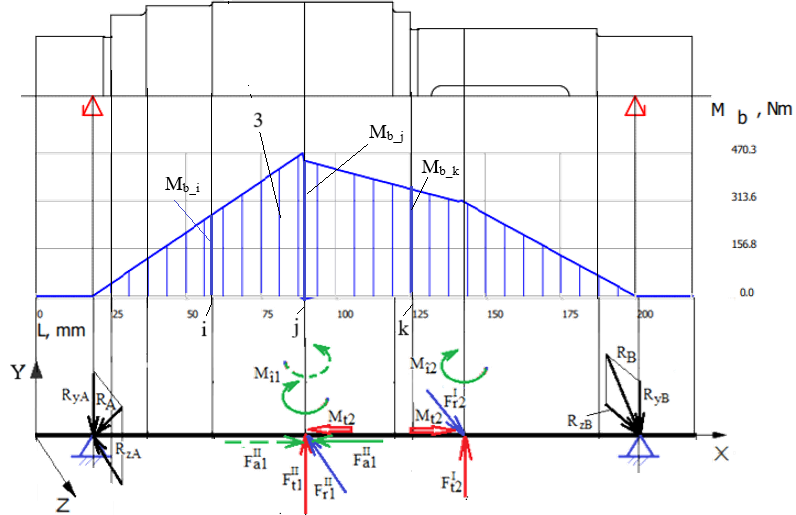
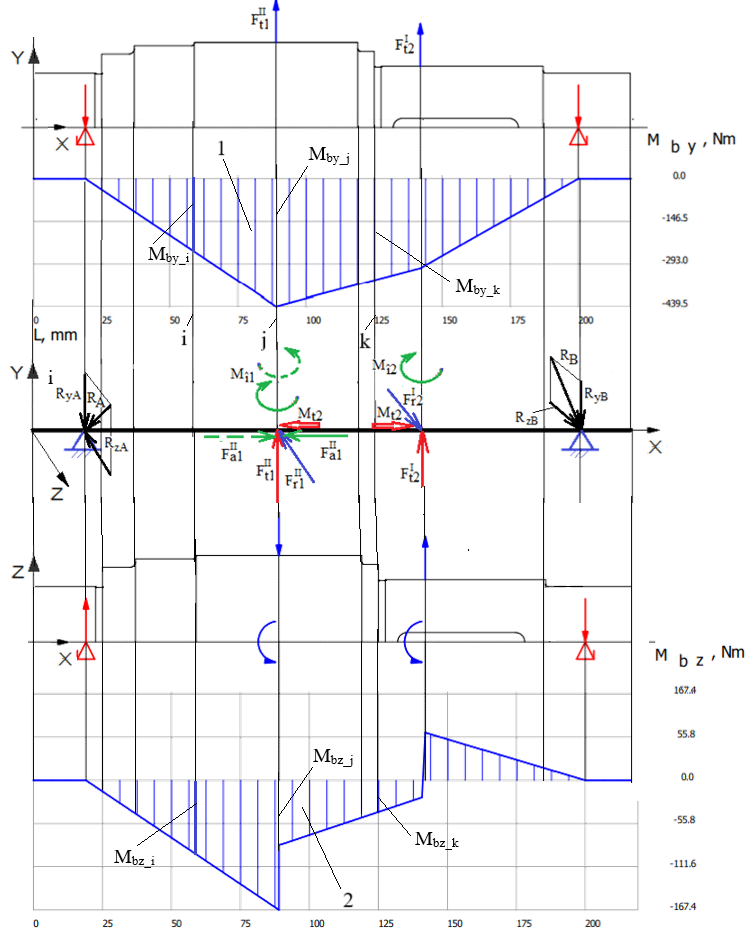
Diagramele momentelor de încovoiere Diagramele momentelor de încovoiere în planele YX și ZX
Diagrama momentului de încovoiere rezultant
Valorile momentului de încovoiere rezultant (diagrama 3) în secțiunea i se determină cu relația, Mb_i =
în care Mby_i și Mbz_i reprezintă momentele de încovoiere din planele YX (diagrama 1) și, respectiv, ZX (diagrama 2) corespunzătoare secțiunii i a arborelui. Valoarea maximă a momentului de încovoiere în secțiunea j se determină cu relația, Mbmax
= Mb_j =
în care Mby_j și Mbz_j reprezintă momentele de încovoiere din planele YX (diagrama 1) și, respectiv, ZX (diagrama 2) corespunzătoare secțiunii j a arborelui.
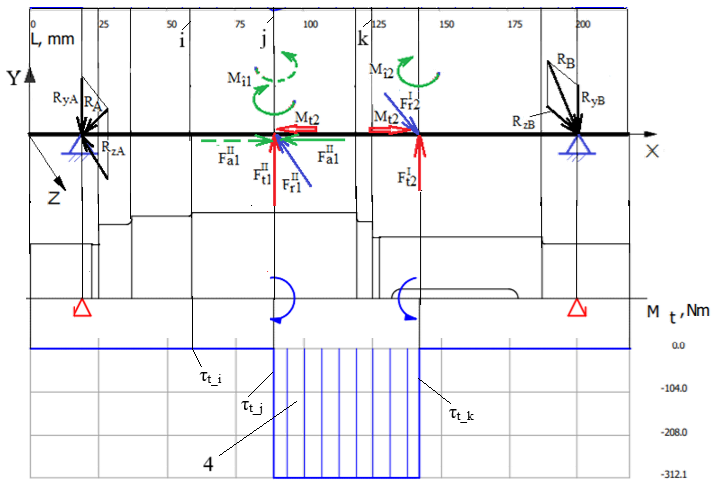
Diagrama momentului de torsiune
Obs. Momentele de torsiune în zona dintre secțiunile j și k sunt egale cu valoarea maximă, Mtmax.
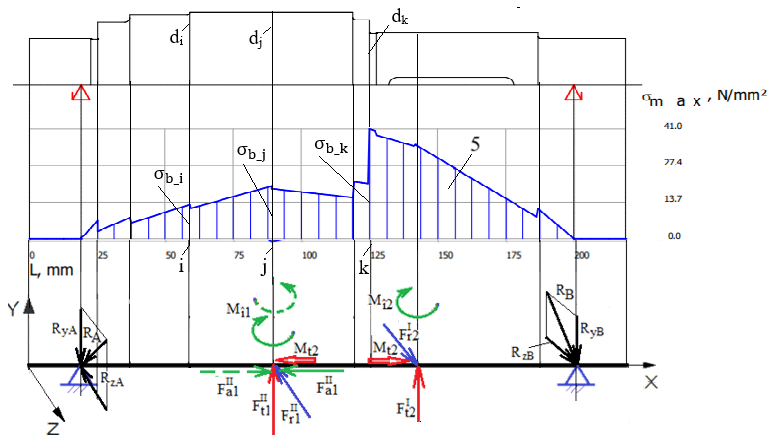
Diagramele tensiunilor Diagramele tensiunilor normale (de încovoiere) rezultante
Valorile tensiunilor normale de încovoiere (diagrama 5) în secțiunea i se determină cu relațiile: σb_i =
în care, Mb_i reprezintă momentul de încovoiere rezultant (diagrama 3), Wti – modulul de rezistență axial, di – diametrul arborelui, toate în această secțiune. Valoarea tensiunii de încovoire maximă (diagrama 5), σbmax
= σb_k =
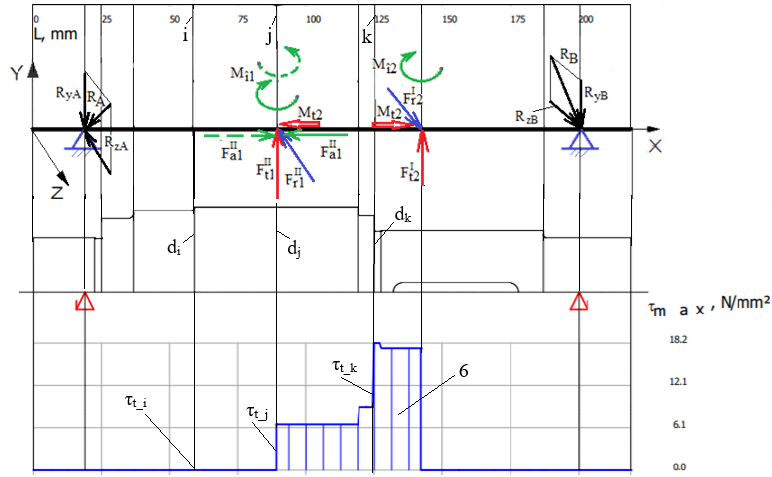
unde, Mb_k reprezintă momentul de încovoiere rezultant din secțiunea k (diagrama 3), dk – diametrul arborelui, ambele în secțiunea k. Diagramele tensiunilor tangențiale (de torsiune)
Valorile tensiunilor tangențiale de torsiune (diagrama 6) se determină cu relațiile: τt_j =
în care, Mt_j reprezintă momentul de torsiune (diagrama 4), Wpj – modulul de rezistență polar, dj – diametrul arborelui, toate în secțiunea j. Valoarea tensiunii tangențiale de torsiune maximă, τmax
= =
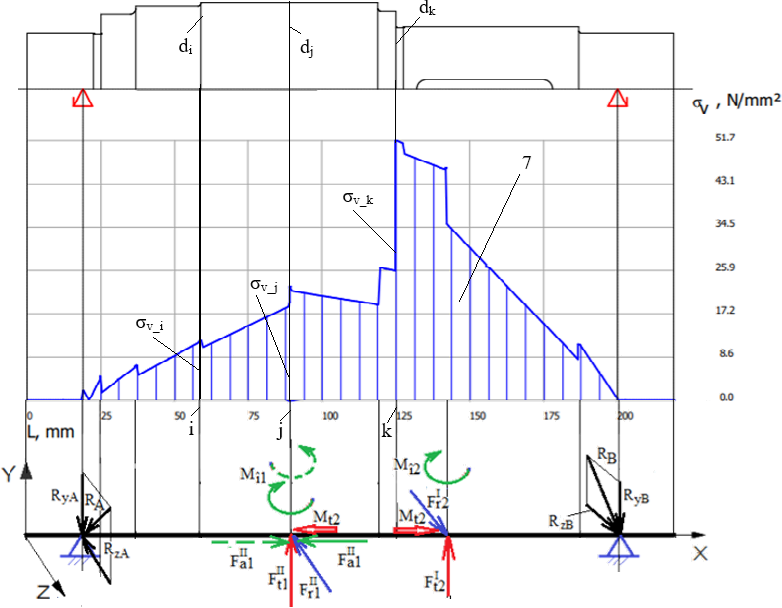
unde Mt_k reprezintă momentul de torsiune (diagrama 4), dk – diametrul arborelui, ambele în secțiunea k. Diagrama tensiunilor echivalente
Valorile tensiunilor echivalente (diagrama 7), conform teoriei de rezistență a III a, se determină cu relația, σv_i =
în care, σb_i reprezintă tensiunea normală de încovoiere rezultantă (diagrama 5), τt_i - tensiunea tangențială de torsiune (diagrama 6), ambele în secțiunea i. Valoarea maximă a tensiunii echivalente, σvmax
= σv_k =
în care, σb_k = σb_k reprezintă tensiunea normală (de încovoiere) rezultantă (diagrama 5), τtmax - tensiunea tangențială de torsiune (diagrama 6), ambele în secțiunea k.
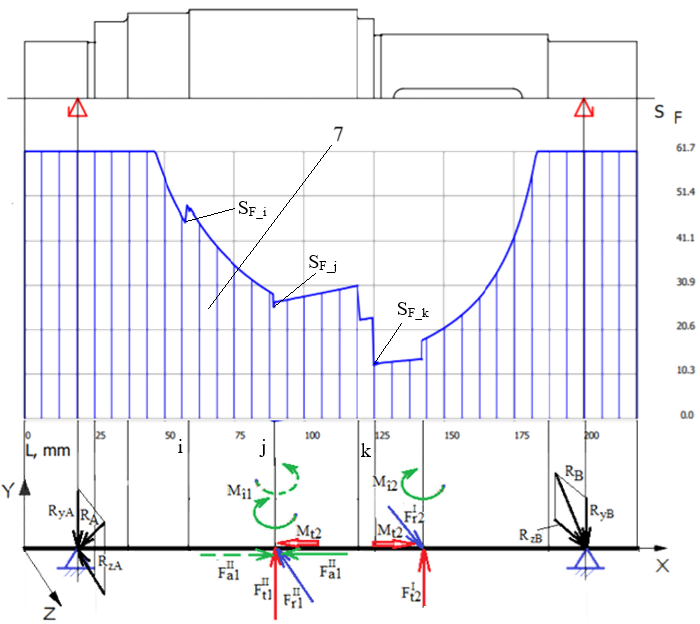
Diagrama coeficienților de siguranță efectivi la solicitări compuse
Obs. Valoarea coeficientului de siguranță efectiv minim la curgere, SFmin = SF_k = SF.
Verificarea la solicitări compuse (încovoiere+torsiune) Calculului de verificare la solicitări compuse se face cu scopul evitării deformării plastice remanente a arborelui intermediar. Verificarea la solicitări compuse (bazat pe tensiunea echivalentă) se face cu relația,
σvmax ≤ σa,
în care, σvmax reprezintă tensiunea echivalentă maximă, σa = σS/SFa cu σS, rezistența la curgere (Yield stress) și SFa, coeficientul de siguranță admisibil (pentru evitarea deformării plastice). Din inegaliatea de mai sus, ținând cont că σa = σS/SFa rezultă,
σS/σvmax ≥ SFa
și notând σS/σvmax = SFmin, coeficientul de siguranță efectiv, se obține a doua formă a relației de verificare la solicitări compuse (bazat pe coeficientul de siguranță),
SFmin ≥ SFa.
Valorile rezistenței la curgere pentru materialul ales, σS = 775 MPa, și coeficientului de siguranță admisibil, SFa = 1,2 (v. subcap. D.3). Exemplu numeric: σvmax ≤ σa, cu σa = σS/SFa = 775/1,2 = 645,83 MPa și σvmax 51,702 MPa ; 51,702 < 645,83 (se verifică). sau, SFmin ≥ SFa cu SFa = 1,2 și SFmin = 12,34; 12,34 > 1,2 (se verifică). Obs. Dacă verificarea nu este îndeplinită se impune mărirea diametrelor tronsoanelor acestuia |
||||||
|
E4. Verificarea la deformații (rigiditate) |
||||||
|
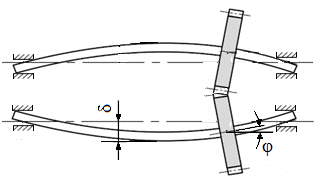
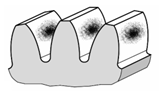
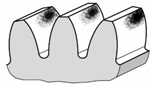
Evidențierea influenței deformațiilor flexionale (de încovoiere) asupra contactelor dinților roților în angrenare (fig. a – schema deformaţiilor elastice ale arborilor unui angrenajului real; fig. b - pata de contact în cazul arborilor perfect rigizi; fig. c – pata de contact în cazul arborilor cu elasticități mărite)
Semnificații: δ – săgeata (deplasarea liniară), φ – rotirea (deplasarea unghiulară).
Diagramele deformațiilor (săgeților și rotirilor)
Obs. Verificarea deformaţiilor flexionale (de încovoiere) În general, se efectuează cu scopul preîntâmpinării funcţionărilor necorespunzătoare (cu vibraţii transversale şi zgomote) ale elementelor susţinute (în special, roţi dinţate) şi a lagărelor cu rulmenți. Această verificare constă în determinarea valorilor săgeţilor sub organele (elementele) susţinute (roţi dinţate) şi a deformaţiilor unghiulare (rotirilor) în lagăre şi limitarea acestora la valori admisibile:
ymax ≤ ya, Θmax ≤ Θa.
Valorile admisibile ale deformaţiilor de încovoiere, recomandate în literatura de specialitate, sunt: - pentru săgeţile de sub roţile dinţate montate pe arbore, ya ≤ (0,01 ... 0,03)mn, mn fiind modulul normal al danturii angrenajului, în mm; - pentru deformaţiile unghiulare (rotirile): Θa = 8.10-3 rad, pentru lagăre cu rulmenţi radiali cu bile; Θa = 2,5.10-3 rad, pentru lagăre cu rulmenţi radiali cu role cilindrice; Θa = 1,7.10-3 rad, pentru lagăre cu rulmenţi radial-axiali cu bile sau cu role conice; Θa= 5.10-2 rad, pentru lagăre cu rulmenţi radial oscilanţi cu bile sau cu role butoi pe două rînduri; Θa = 10-3 rad, pentru lagăre cu alunecare; - pentru arborii reductoarelor de turație se recomandă, ya = (2…3).10-4 L, unde L [mm] este distanța dintre reazeme (lagăre). Obs. Dacă deformaţiile efective nu sunt mai mici decât cele recomandate în literatura de specialitate (nu sunt îndeplinite condiţiile de verificare), se măreşte rigiditatea arborelui la încovoiere, prin mărirea diametrelor tronsoanelor acestuia. Exemplu numeric: - verificarea la deformații liniare (săgeți) în zona angrenajului (secțiunea j), y ≤ ya; ya = (0,01…0,03)*4 = 0,04…0,12 mm; 0,012767 < 0,04…0,12 mm (se verifică) - verificarea la deformații liniare (săgeți) maxime: ymax ≤ ya; ya = 2,5*10-4 *181 = 0,0452 mm; 0,015214 < 0,0452 mm (se verifică); - verificare la deformații unghiulare (rotiri) maxime în lagăre: Θmax ≤ Θa; θa = 1,7.10-3 rad = 1,7.10-3*180/π = 0,097o. 0,018449 < 0,97 o (se verifică).
Verificarea deformaţiilor torsionale ( de răsucire) Acest calcul presupune determinarea valorilor unghiurilor de răsucire (rotirilor axiale) ale arborelui şi limitarea acestora la valori admisibile,
φ ≤ φa.
Valorile admisibile pentru unghiul de torsiune (răsucire), determinate de destinaţia arborelui, recomandate în literatura de specialitate, sunt: φa = (15 ... 25) . 10-2 rad/m, pentru arborii diferenţialelor autovehiculelor (arborii planetari); φa = (40 ... 55) 10-4 rad/m, pentru arborii mecanismelor de deplasare ale podurilor rulante. În cazul arborilor scurţi (reductoare de uz general, cutii de viteze etc.), în general, rigiditatea la torsiune nu are rol esenţial şi, ca urmare, pentru calculul la deformaţii torsionale se poate considera, φa = (25 ... 50) 10-4 rad/m. Obs. În cazul în care unghiurile efective de torsiune (răsucire) depăşesc valorile recomandate în literatura de specialitate, se mărește rigiditatea arborelui la torsiune, prin mărirea diametrelor tronsoanelor acestuia. Exemplu numeric: Unghiul de rotire calculat de MDESIGN,
0,015 ≤ (25…50) . 10-4 180/π; 0,015 ≤ (0,14 …2,8) o/m (se verifică) |
||||||
|
E.5 Verificarea la oboseală (solicitări variabile) |
||||||
|
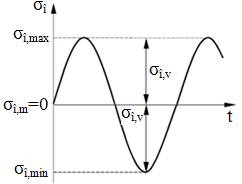
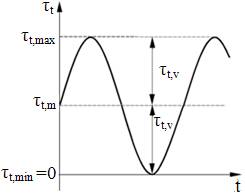
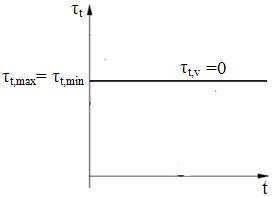
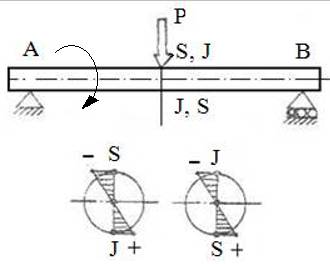
Ciclurile de variație a tensiunilor (fig: a – alternant simetric (frecvent, pentru încovoiere, conform figurii de mai sus); fig. b - pulsator (frecvent, pentru torsiune); fig. c – constant (pentru, torsiune, fig. d – schematizarea variației tensiunii de încovoiere în plan transversal)
a b c
d Obs. Ciclul alternant simetric al tensiunilor de încovoiere este generat de mișcarea de rotație a arborelui (fig. d) astfel: la un moment dat fibra de sus (S) este solicitată la compresiune (tensiune negativă) și fibra de jos (J) la tracțiune (tensiune pozitivă); după o rotație cu 180o (o jumătate de perioadă) procesul este invers.
Diagrama coeficienților de siguranță la oboseală (solicitări variabile)
Calculul la solicitări variabile (oboseală), în general, se efectuează în vederea preîntâmpinării ruperii arborilor prin fisurare, cu precădere, în zona concentratorilor de tensiune. Condiţia rezistenţei la oboseală a arborilor drepţi în zonele care există concentratori de tensiuni (canale de pană, caneluri, salturi de diametre, găuri transversale, filet, ajustaje presate etc.), cu precădere, supuşi la solicitări compuse (torsiune şi încovoiere) este dată de relaţia,
SDmin ≥ SDa,
în care SDmin, reprezintă coeficientul de siguranță minim, obținut prin calcul, și SD coeficientul de siguranță admisibil (s-a introdus ca dată de intrarea SDa = 1,2). Obs. Dacă nu se verifică la oboseală se pot modifica zonele concentratorilor de tensiune. Exemplu numeric: SDmin ≥ SD; 3,32 > 1,2 (se verifică) |
||||||
|
E.6 Verificare la vibrații |
||||||
|
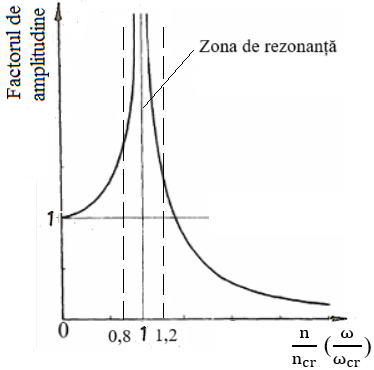
Frecvenţa (pulsația) proprie este o caracteristică a unui sistem oscilant independentă de condiţiile iniţiale ale mişcării. În cazul arborilor elastici, frecvența (pulsația) proprie a vibraţiilor flexionale sau torsionale se numeşte turație (pulsație) critică. Un arbore care are turația de funcționare egală cu turația critică (n = ncr ) forța elastică și forța de inerție se echilibrează reciproc iar forța perturbatoare excitatoare (de obicei, forța centrifugă) produce creșterea rapidă a amplitudinii mășcării (deformării arborelui), aceasta ajungând la valori foarte mari (teoretic, la ∞) și are loc fenomenul de rezonanță.
Verificarea la vibrații cu scopul evitării rezonanței se face cu relația,
n ≠ (0,8…1,2) nb,
unde, nb reprezintă turația critică de încovoiere sau de torsiune (determinată cu MDESIGN), n – turaţia maximă de funcționare a arborelui. Obs. De obicei, pentru turația critică de încovoiere sau de torsiune se adoptă prima turație proprie (linia 1 din tabelele de mai jos)
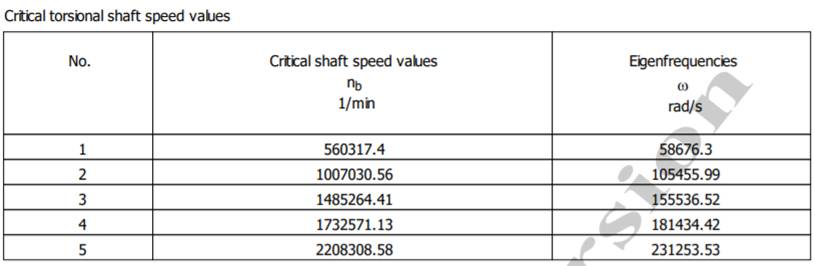
Turațiile și pulsațiile critice la torsiune
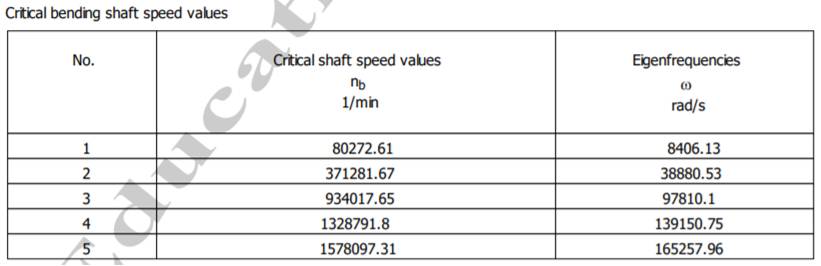
Turațiile și pulsațiile critice la încovoiere
Exemplu numeric: - pentru vibrații torsionale, n ≠ (0,8…1,2) nb_î: 625 ≠ (0,8…1,2) 560317,4; 625 ≠ (448254,24…672388,88) rot/min (se verifică). - pentru vibrații flexionale (de încovoiere), n ≠ (0,8…1,2) nb_t: 625 ≠ (0,8…1,2) 80272,61; 625 ≠ (64218,1…96327,13) rot/min (se verifică) |
 k
k