|
autori Organe de Mașini. Lucrări de laborator. Universitatea Transilvania din Brașov
|
||||||||||||
|
Lucrarea LD.OM II.03 ANGRENAJE ȘI ROȚI DINȚATE
|
||||||||||||
|
CUPRINS |
||||||||||||
|
A. DESCRIEREA TEMATICII B. BAZE TEORETICE ELEMENTARE C. SCHEME STRUCTURAL-FUNCȚIONALE ȘI SOLUȚII CONSTRUCTIVE |
||||||||||||
|
DESCRIEREA TEMATICII |
||||||||||||
|
A.1 Aspecte generale |
||||||||||||
|
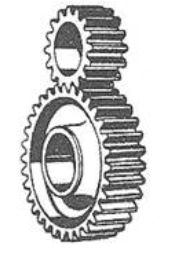
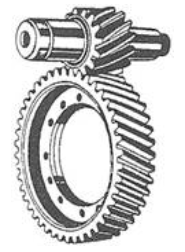
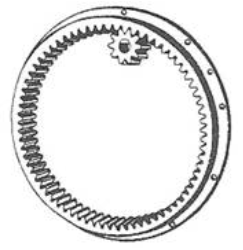
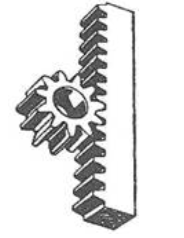
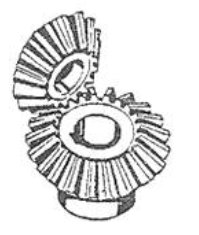
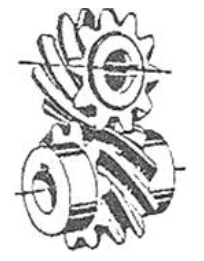
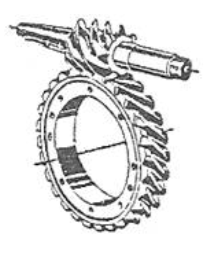
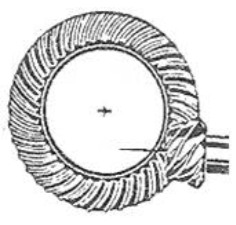
Mecanismele cu roți dințate sunt frecvent întâlnite în componența unor transmisii dedicate: cutii de viteze, reductoare de turație, multiplicatoare de turație, transmisii diferențiale, transportoare, utilaje tehnologice etc. Acestea s-au impus față de alte tipuri de transmisii (prin curele, lanțuri etc.) pe scară largă datorită avantajelor: capacitate portantă mărită (gabarite reduse), randament mărit, durabilitate ridicată, raport de transmitere constant, siguranță în exploatare precum și posibilitatea utilizării pentru domenii largi de puteri, viteze, rapoarte de transmitere. Pe de altă parte, acestea au și dezavantaje: precizii de execuție și montaj ridicate, tehnologii complexe (costuri ridicate), zgomote și vibrații în exploatare, rapoarte de transmitere discrete (numerele de dinți ale roților sunt numere întregi). Preponderența avantajelor în raport cu dezavantajele provine, cu precădere, din concepția acestora bazată pe curba flancurilor active de tip evolventă care asigură performanțe funcționale, constructive și tehnologice majore. (https://rrv.unitbv.ro/mg/SIOM/AEV/AEV/AEV-T.1.htm; https://www.youtube.com/watch?v=nrsCoQN6V4M) În practica construcției autovehiculelor se întâlnesc frecvent următoarele angrenaje:
|
||||||||||||
|
A.2 Scopul lucrării |
||||||||||||
|
Prin efectuarea lucrării de laborator se urmărește cunoașterea tipurilor de angrenaje și de roți dințate precum și a construcțiilor acestora, urmărind cu precădere: - determinarea caracteristicilor funcționale (geometrice, cinematice, cinetostatice); - cunoașterea construcției și tehnologiei de obținere; - identificarea prin măsurare a parametrilor roților dințate și angrenajelor |
||||||||||||
|
A. BAZE TEORETICE ELEMENTARE |
||||||||||||
|
B.1 Descriere funcțional-constructivă |
||||||||||||
|
Roata dințată este elementul de mașină care are la periferie z dinți dispuși echiunghiular. Pinion roata dințată a unui angrenaj cu numărul minim de dinți. Angrenarea este procesul de contact succesiv și continuu al dinților roților conjugate ale unui angrenaj în vederea transmiterii mișcării neîntrerupt |
||||||||||||
|
B.2 Modele și relații de calcul elementare |
||||||||||||
|
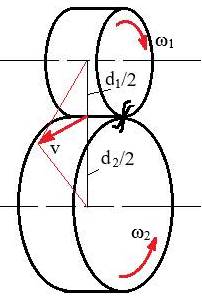
Angrenaje și roți dințate cilindrice Cinematica angrenajului cilindric
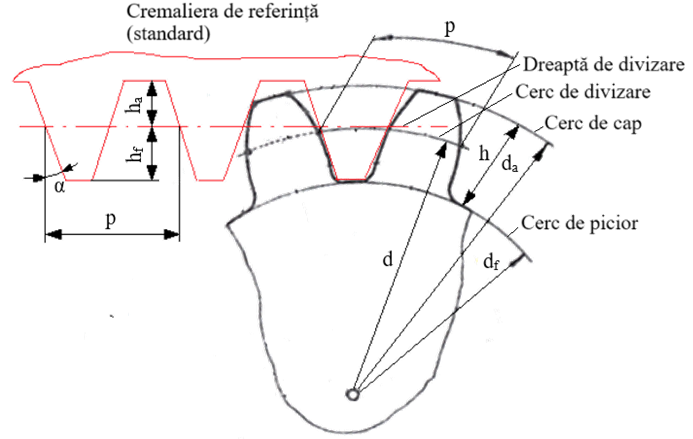
Semnificații notații: ω1 viteza unghiulară a pinionului (roata mai mică); ω2 viteza unghiulară a roții; d1 diametrul de divizare al pinionului; d2 diametrul de divizare al roții; v viteza periferică (în punctul de tangență a cercurilor de divizare). Geometrie de bază pentru roți dințate cilindrice cu dantură dreaptă Semnificații notații: d diametrul de divizare, da diametrul cercului de cap, df diametrul cercului de picior, p pasul cremalierei (egal cu pasul circular), da diametrul cercului de cap, α unghiul cremalierei de referință (de presiune), ha înălțimea capului dintelui; hf înălțimea piciorului dintelui; h înălțimea dintelui. Profilul dintelui este curba de tip evolventă asociată flancurilor dinților roților, https://rrv.unitbv.ro/SIOM/AEV/AEV/AEV-T.1.htm Pasul circular, p = m π, unde m [mm] reprezintă modulul. Lungimea cercului de divizare, z p = π d, sau z m π = π d; după simplificare rezultă, diametrul de divizare, d = m z (z, reprezintă numărul de dinți ai roții). Cremaliera de referință a unei roți dințate se obține mărind fictiv numărul de dinți la ∞ și prrofilil evolventic degenerează în linie dreaptă. Parametri principali ai
cremalierei de referință standard (pasul cremalierei este egal pasul
circular al roții): α = 200
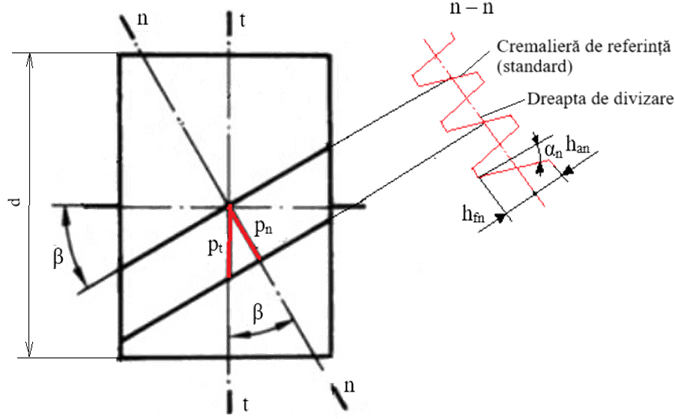
(unghiul de presiune), ha = Diametrul cercului de cap, da = d + 2ha = mz + 2m sau da = m(z + 2). Diametrul cercului de picior, df = d - 2hf = mz + 2*1,25m sau da = m(z 2,5). Geometrie de bază pentru roți dințate cilindrice nedeplasate cu dantură înclinată
Semnificații notații: d diametrul de divizare, β unghiul de înclinare al danturii, pt pasul frontal, pn pasul normal, han înălțimea capului dintelui în plan normal; hfn înălțimea piciorului dintelui în plan normal; α unghiul cremalierei de referință (de presiune) în plan normal. Profilul dintelui se reprezintă (descrie) în două plane: t t plan frontal, perpendicular pe axa roții; n n plan normal, perpendicular pe direcția dintelui înclinată (la nivelul cercului de divizare) cu unghiul β. Cremaliera
de referința standard din planul normal are parametrii principali
(asociați și sculelor de generare): mn
[mm] reprezintă modulul normal standardizat, αn
= 200 (unghiul de presiune în plan normal), han = Obs. Geometria roții se descrie în plan frontal (t-t) luând în considerare modulul standard din planul normal (n-n) Diametrul
de divizare (în plan frontal), d = m z = Diametrul cercului de cap
(în plan frontal), da = d + 2 han
= Diametrul cercului de picior,
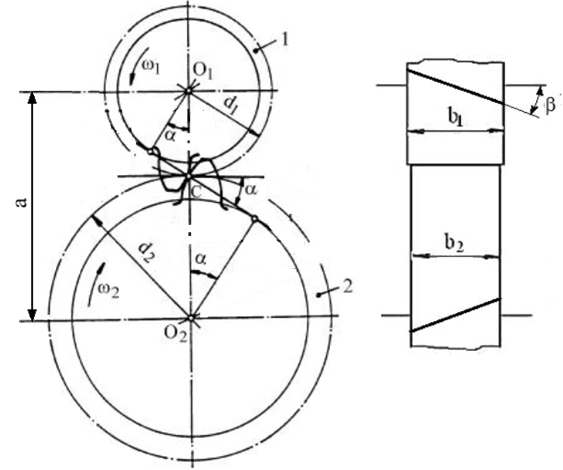
df = d - 2 hfn. = Avantajele angrenajelor cilindrice cu dantură înclinată față de cele cu dantură dreaptă: - în cazul execuției din același material (oțel) au capacități portante mărite (transmit momente de torsiune mai mari) sau dacă sunt încărcate cu același moment de torsiune au gabarite (mase) mai mici; - funcționare cu zgomote reduse deoarece dinții intră/ies progresiv în/din angrenare. Geometria de bază a angrenajului cilindric nedeplasat
Semnificații notații: a distanța dintre axe, b1 lățimea pinionului, b2 lățimea roții. Distanța dintre axe (de referință) a unui angrenaj nedeplasat, a =
Lățimile danturilor, din considerente de montaj facil, b2 = b1 + (4 6) mm. Danturi modificate (deplasate) Schemele deplasărilor danturilor
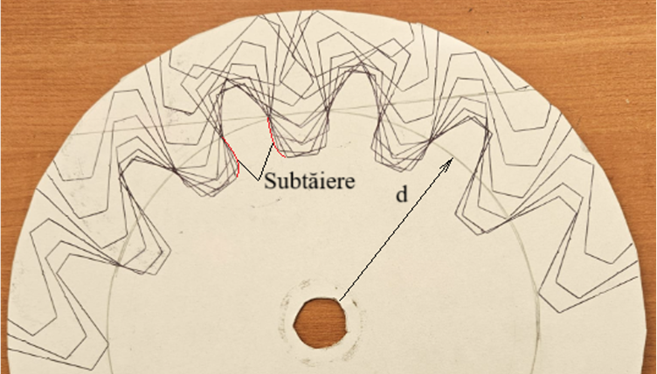
Caracteristici danturilor deplasate cu xm sau xmn, unde x (pozitiv sau negativ) reprezintă factorul deplasării: - danturile deplasate MINUS pot conduce la dinți subtăiați care se comportă necorespunzător în funcționare și deci trebuie evitate; - danturile deplasate PLUS conduc la profile cu raze de curbură mărite și la dinți îngroșați spre baza dintelui ce asigură rezistențe (la oboseală) la contact și, respectiv, la încovoiere mărite; deci, sunt preferate în practică urmărind să se evite ascuțirea dinților. Numerele de dinți ai roților dințate cilindrice, în practică, z ≥ zlim cu valoarea limită zlim =14 dinți; pentru valori mai mici apare subtăierea dintelui (v. ex. de mai jos cu z = 12 dinți) Simularea generării dinților roților dințate (inclusiv cele deplasate) cu profil evolventic prin rulare Descrierea dispozitivului
Modulul danturii: cunoscând (prin măsurare) valoarea pasului, p = 47,1 mm și ținând cont că p = m π, rezultă m = p/π = 47,12/π = 14,99; deci valoarea standard a modulului, m = 15 mm. Diametrul de divizare: cunoscând (prin măsurare) valoarea d = 90 mm și ținând cont că d = m z, rezultă z = d/m = 90/15 = 12 dinți. Aplicații de generare profile a. dantură nedeplasată: z = 12 dinți, m = 15 mm, d = 90 mm.
Obs. Se observă că se obține dantură subtăiată deoarece, z < zlim (12 < 14). b. dantură deplasată PLUS: mx = +4 mm, z = 12 dinți, m = 15 mm, d = 90 mm, x = +4/15 = +0,266.
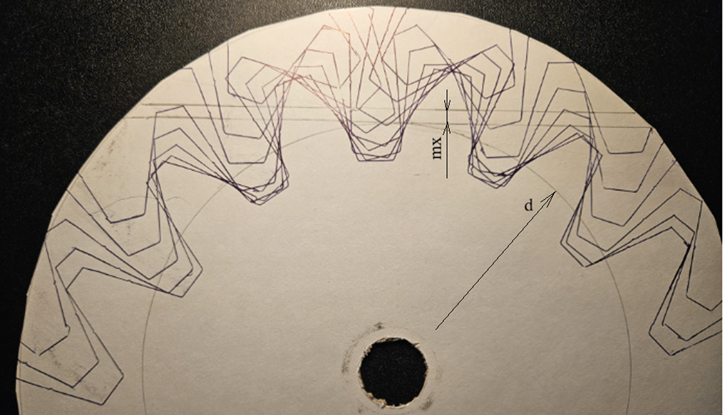
Obs. Se observă că se obține dantură ascuțită deoarece mx = +4mm este mult prea mare. c. dantură deplasată: mx = +2,5 mm, z = 12 dinți, m = 15 mm, d = 90 mm, x = +2,5/15 = +0,166.
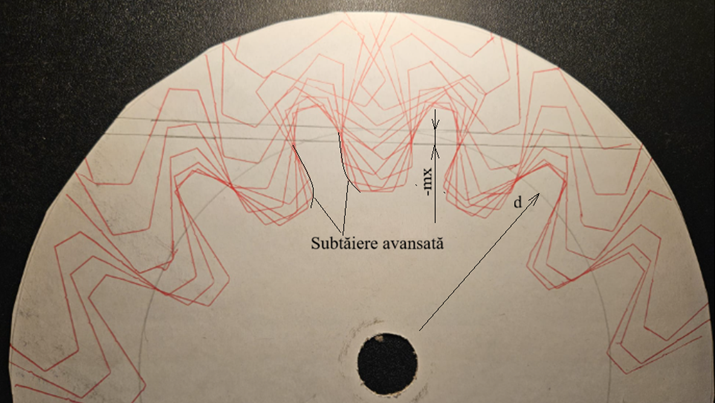
Obs. Se observă că se obține dantură neascuțită cu grosimea dintelui la cap, 1,5 mm (soluție acceptabilă din punct de vedere funcțional chiar dacă roata are z 12 dinți). d. dantură deplasată: -mx = -5 mm, z = 12 dinți, m = 15 mm, d = 90 mm, x = -5/15 = - 0,33.
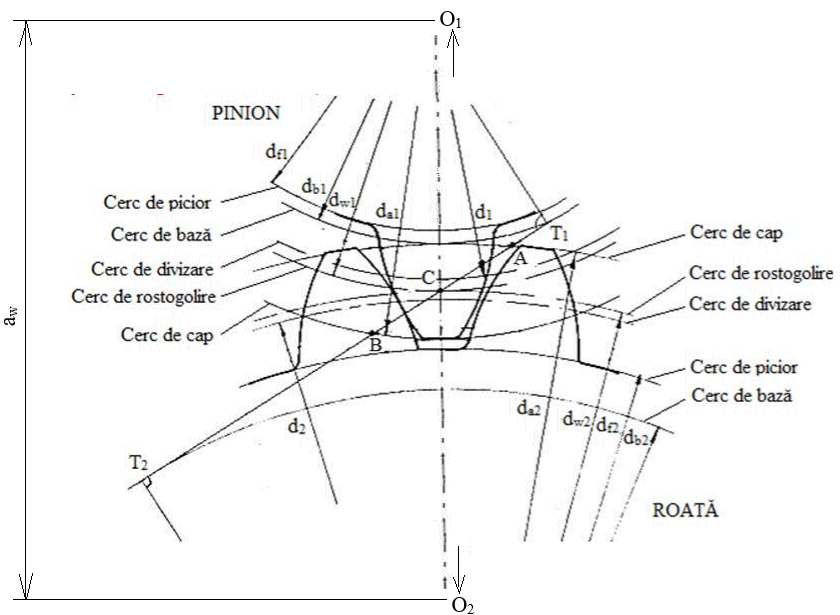
Obs. Se observă că se obține dantură subtăiată deoarece, z < zlim (12 < 14) și, în plus, deplasare MINUS cu mx = - 5 mm. Geometria angrenajului PLUS
Semnificații notații: C polul angrenării, AB - segmentul real de angrenare, aw - distanța dintre axe a angrenajului deplasat; db1 diametrul cercului de bază al pinionului, db2 diametrul cercului de bază al roții, da1 diametrul cercului de cap al pinionului, da2 diametrul cercului de cap al roții, d1 diametrul cercului de divizare al pinionului, d2 diametrul cercului de divizare al roții, dw1 diametrul cercului de rostogolire al pinionului, dw2 diametrul cercului de rostogolire al roții, df1 diametrul cercului de picior al pinionului, da2 diametrul cercului de picior al roții. - Cercurile de divizare nu mai sunt tangente ca la angrenajul de referință (nedeplasat); apar cercurile de rostogolire care sunt tangente. - Distanța dintre axe a angrenajului cilindric deplasat PLUS, aw > a, unde a este distanța dintre axe a angrenajului de referință (nedeplasat) (v. mai sus). Realizarea distanței dintre axe impusă prin deplasarea danturii, Angrenajul PLUS vs angrenajul NEDEPLASAT
Din figură se observă următoarele: - distanța dintre axe impusă este mai mare decât distanța dintre axe de referință, aw > a; - deoarece atât pinionul cât și roata au deplasări PLUS dinții acestora sunt îngoșați și deci, se asigură rezistențe la oboseala de contact și de încovoiere mărite; Obs. În practică în cazurile distanțelor dintre axe impusă (aw ) și de referință (a) sunt apropiate (-0,5mn < aw a ≤ mn) se pot găsi depalsările necesare pentru asigurarea distanței dintre axe impusă, desigur cu păstrarea numerelor de dinți (raportului de transmitere), v. rrv.unitbv.ro/RConCil/deplasare Simularea angrenării, Prin parcurgerea algoritmului rrv.unitbv.ro/RConCil/simulare se poate evidenția infuența valorilor deplasărilor danturilor roților asupra gradului de acoperire.
Angrenaje și roți dințate conice Cinematica angrenajului conic
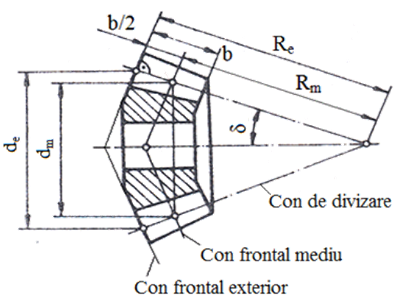
Semnificații notații: ω1 viteza unghiulară a pinionului (roata mai mică); ω2 viteza unghiulară a roții; dm1 diametrul mediu al pinionului; dm2 diametrul mediu al roții; v viteza periferică (în punctul de tangență a cercurilor de divizare medii), δ1 semiunghiul conului de divizare al pinionului, δ1 unghiul conului de divizare al roții. Geometria de bază a roților angrenajului conic ortogonal
Semnificații notații: δ semiunghiul conului de divizare, b lățimea danturii, dm diametrul mediu, de diametrul exterior, Re generatoarea conului exterior, Rm generatoarea conului mediu. Definirea geometriei se face corespunzător conului frontal exterior unde apar următorii patrametri caracteristici: me [mm] modulul frontal exterior (are valori standard pentru dantură dreaptă sau valori corespunzătoare tehnologiei, pentru dantură curbă), de = me z diametrul de divizare exterior, Încărcarea cu forțe precum și calculele de rezistență (la oboseală) se realizează corespunzător conului frontal mediu unde apar următorii patrametri caracteristici: mm [mm] modulul frontal mediu, dm = mm z diametrul de divizare mediu. Avantajele angrenajelor conice cu dantură curbă față de cele cu dantură dreaptă: - în cazul execuției din același material (oțel) au capacități portante mărite (transmit momente de torsiune mai mari) sau dacă sunt încărcate cu același moment de torsiune au gabarite (mase) mai mici; - funcționare cu zgomote reduse deoarece dinții intră/ies progresiv în/din angrenare. Asamblarea roților dințate ale angrenajelor conice Montajul roților dințate conice în vederea angrenării corespunzătoare imlpică verificări și reglări preliminare (https://www.youtube.com/watch?v=1JBR5MOpXB8, https://www.youtube.com/watch?v=Zi9PBZCgw-0&t=3s).
Angrenaje și roți dințate melcate
|
||||||||||||
|
B. SCHEME STRUCTURAL-FUNCȚIONALE ȘI SOLUȚII CONSTRUCTIVE |
||||||||||||
|
C.1 Identificare parametri funcționali |
||||||||||||
|
Identificarea modulului unei roți dințate cu dantură dreaptă nedeplasată prin măsurarea cu șublerul a înălțimii capului dintelui Poziționarea tijei de adâncime a șublerului
Fixarea vernierului (pentru măsurarea cu șublerul v. https://www.youtube.com/watch?v=eawNHOJp960)
La citire se identifică h = 11,2 mm; ținând cont că h = 2,25 m (v. mai sus), rezultă m = h/2,25 = 11,2/2,25 = 4,97 mm; deci valoarea standard a modulului frontal m = 5 mm. Identificarea modulului unei roți dințate cu dantură dreaptă nedeplasată prin măsurarea cu șublerul a diametrului de cap (pentru roțile cu număr par de dinți) Poziționarea flancurilor de exterior ale șublerului
Fixarea vernierului (pentru măsurarea cu șublerul v. https://www.youtube.com/watch?v=eawNHOJp960)
La citire se identifică diametrul cercului de cap da = 11,2 mm; ținând cont că da = m (z +2) (v. mai sus), rezultă m = da/(z+2) = 79,75/(14+2) = 4,97 mm; deci, valoarea standard a modulului frontal m = 5 mm. Determinarea raportului de transmitere/angrenare Pentru angrenajul din figură în urma numărării dinților roților rezultă: raportul de transmitere, i = -15/10 = -1,5, și raportul de angrenare u = 1,5.
|
||||||||||||
|
C.1 Forme constructive |
||||||||||||
|
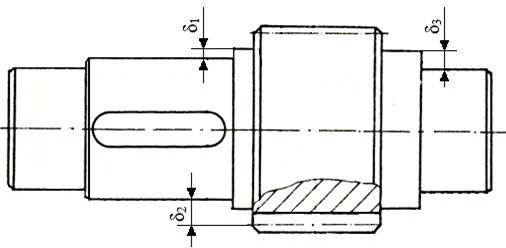
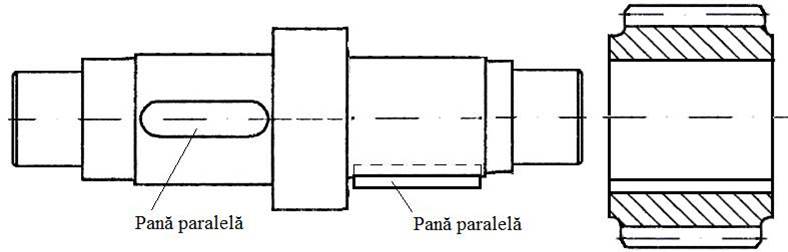
Roți pentru angrenaje cilindrice Pinioane cilindrice Varianta I. Arbore intermediar corp comun cu pinionul cilindric
Varianta II. Arbore intermediar corp comun cu pinionul cilindric cu dimensiuni radiale reduse
Varianta III. Arbore intermediar și pinionul cilindric separate
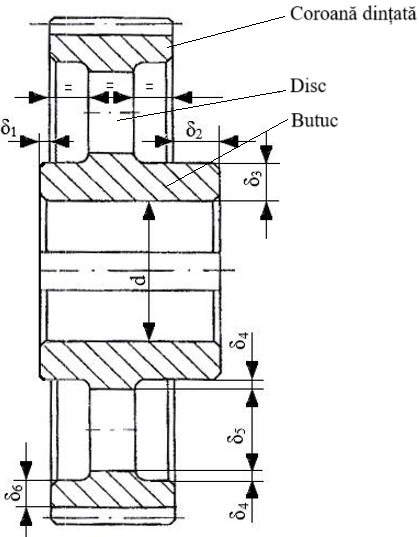
Obs. Oțelul din care se execută arborele are rezistențe mecanice mai mici decât ale pinionului în varianta III; în cazul pinionului corp comun cu arborele (varaiantele I și II) se adoptă pentru arbore același oțel ca al pinionului. Roți dințate cilindrice Varianta I. Roată dințată cilindrică cu butuc asimetric
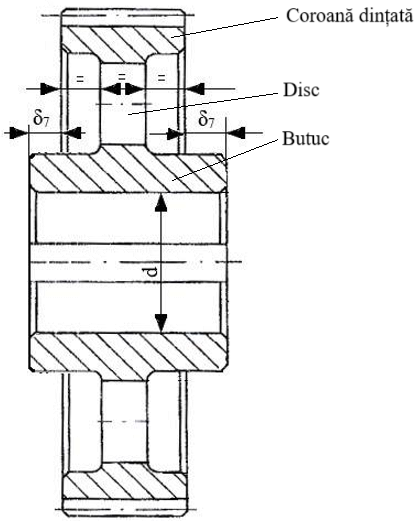
Varianta II. Roată dințată cilindrică cu butuc simetric
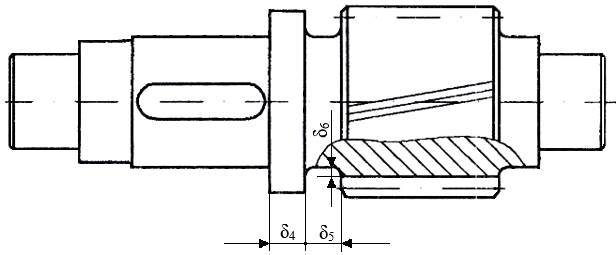
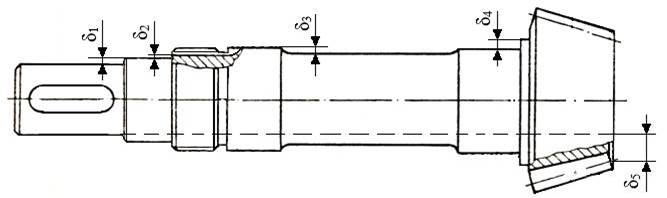
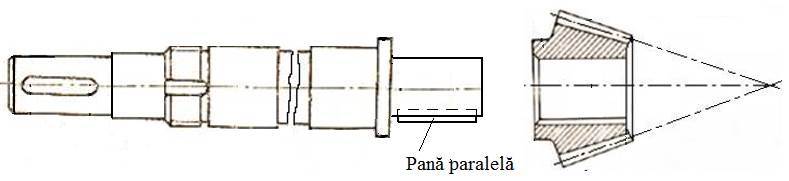
Roți pentru angrenaje cilindrice Pinioane conice Varianta I. Arbore de intrare corp comun cu pinionul conic
Varianta II. Arbore de intrare și pinionul conic separate
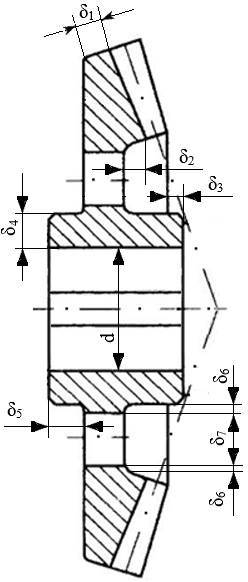
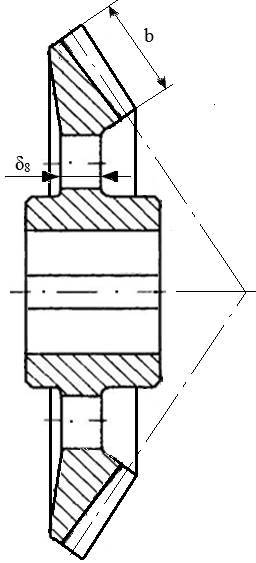
Roți dințate cilindrice Varianta I. Roată dințată conică cu unghiul conului de divizare mărit
Varianta II. Roată dințată conică cu unghiul conului de divizare redus
|
||||||||||||
|
C2. Măsurare parametri geometrici |
||||||||||||
|
Roți dințate cilindrice Măsurarea cotei peste n dinți cu micrometrul cu talere Poziționarea talerelor micrometrului
Fixarea poziției vernierului în urma acționării clichetului (pentru măsurarea cu micrometrul v. https://www.youtube.com/watch?v=UgxNUcbjS0A)
La citire se identifică lungimea peste 5 dinți, W5 = 67,14 mm. |
||||||||||||
|
C2. Tehnologii de prelucrare |
||||||||||||
|
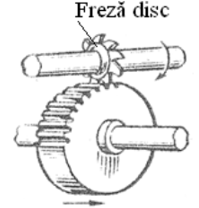
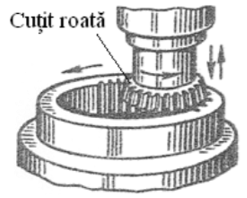
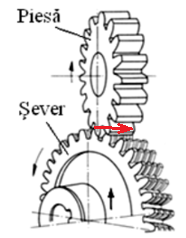
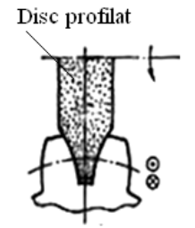
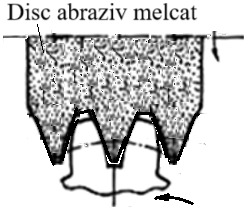
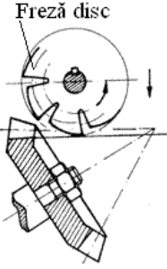
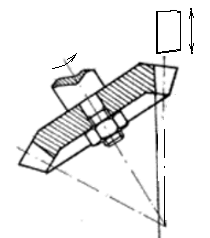
Pentru danturi cilindrice
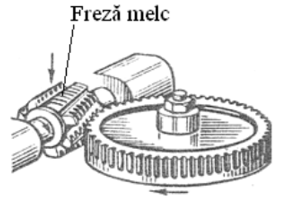
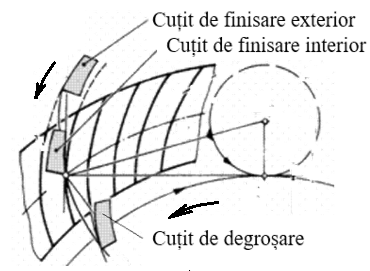
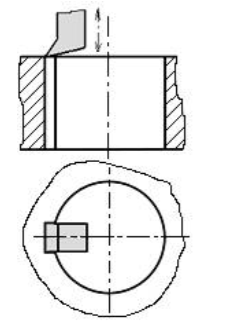
Pentru danturi conice
|